Самостоятельные работы по алгебре по теме «Функции и их свойства» содержат в себе как теоретические вопросы по теме (представленные в виде тестов открытого типа, т. е. тесты с добавлением), так и практические вопросы по теме (они представлены в виде тестов закрытого типа с альтернативным выбором ответа, а также в виде тестов открытого типа со свободным изложением). Самостоятельные работы как контроль знаний по теме «Функции и их свойства» ориентированы на учебник алгебры авторов Ю.Н. Макарычев, Н.Г. Миндюк и др. Также их могут использовать учителя, работающие по другим учебникам при подготовке обучающихся к ОГЭ.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Серия самостоятельных работ по теме "Функции и их свойства"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Тест по функциями их свойствам»
Просмотр содержимого документа
«Функции и их свойства_самост. раб.»
Просмотр содержимого документа
«Функции и их свойства_теория и практика»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1540 руб.
2560 руб.
1690 руб.
2820 руб.
1800 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
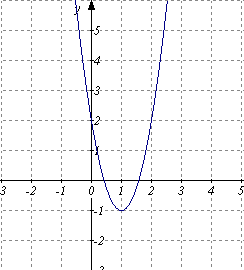
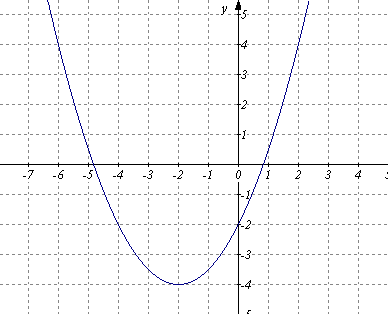
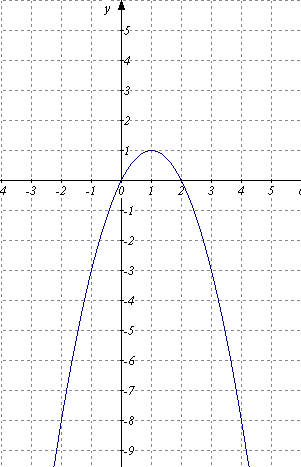 ) Б) В)
) Б) В)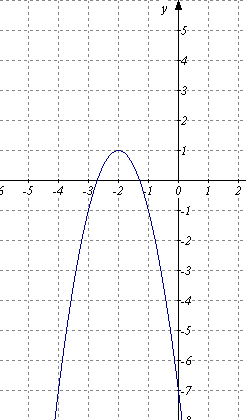 )
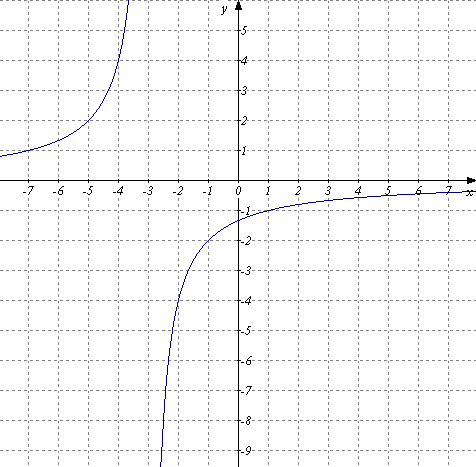
) 
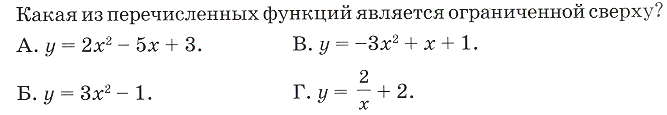
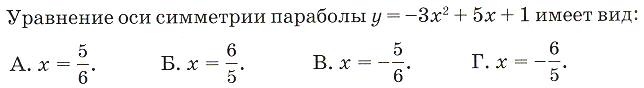
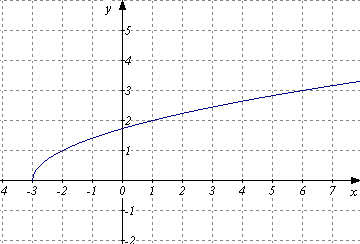
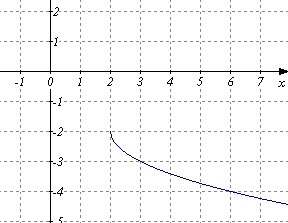
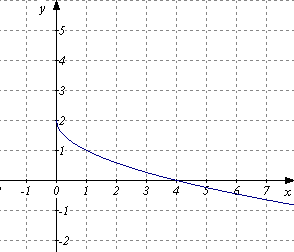
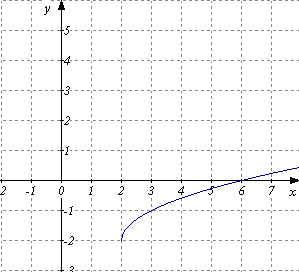 ) Г)
) Г) 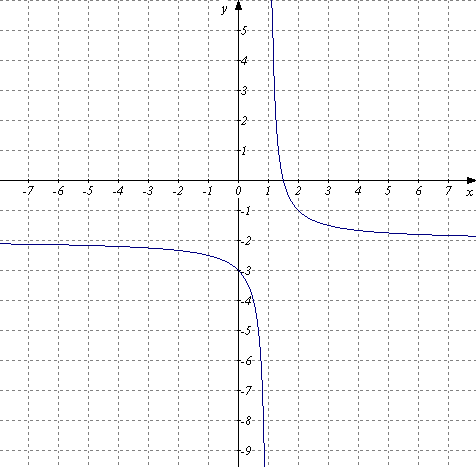
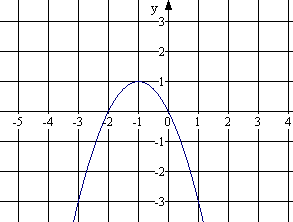
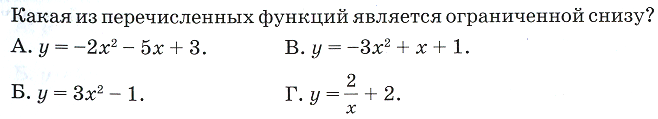 айдите наибольшее (наименьшее) значение функции
айдите наибольшее (наименьшее) значение функции 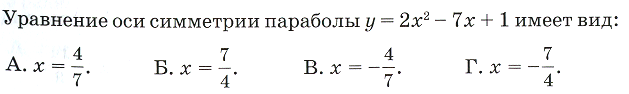
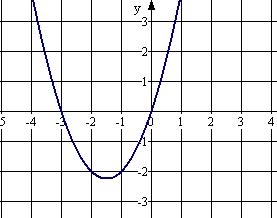
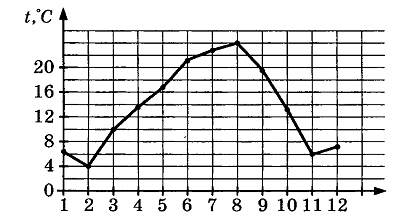
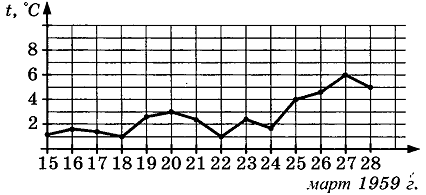 . На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какой была наибольшая среднесуточная температура в период с 17 марта по 24 марта. Ответ дайте в градусах Цельсия.
. На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 года. По горизонтали указываются числа месяца, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какой была наибольшая среднесуточная температура в период с 17 марта по 24 марта. Ответ дайте в градусах Цельсия.  : __________________________________________________________________________________.
: __________________________________________________________________________________.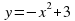 равно _____________.
равно _____________.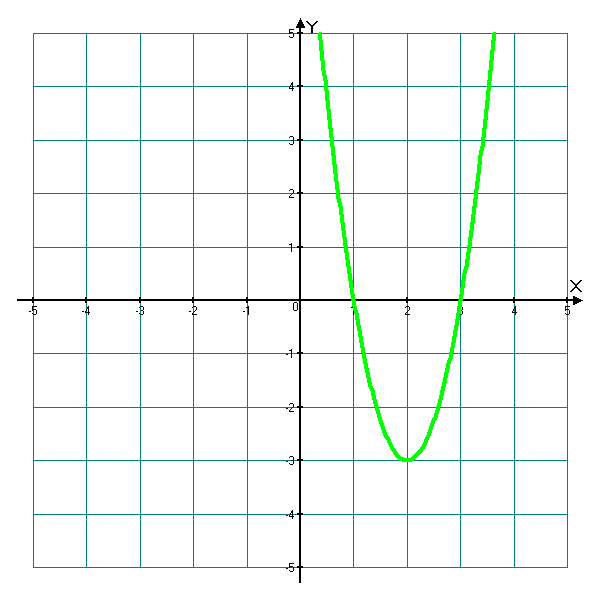
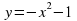 : _________________________________________________________________________________.
: _________________________________________________________________________________.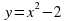 равно _____________.
равно _____________.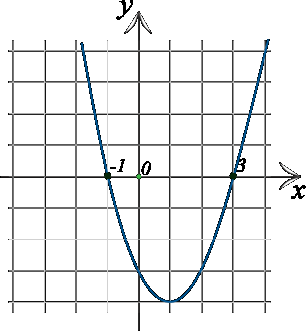
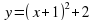 : __________________________________________________________________________________.
: __________________________________________________________________________________.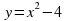 ___________________________________________________.
___________________________________________________.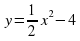 : __________________________________________________________________________________.
: __________________________________________________________________________________.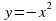 возрастает на промежутке _________________ и убывает на промежутке __________________.
возрастает на промежутке _________________ и убывает на промежутке __________________.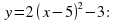 __________________________________________________________________________________.
__________________________________________________________________________________.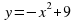 __________________________________________________.
__________________________________________________.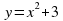 : _________________________________________________________________________________.
: _________________________________________________________________________________.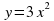 убывает на промежутке _________________ и возрастает на промежутке __________________.
убывает на промежутке _________________ и возрастает на промежутке __________________.















