Муниципальное бюджетное общеобразовательное учреждение
"Многопрофильный лицей" городского поселения "Рабочий поселок Чегдомын" Верхнебуреинского муниципального
района Хабаровского края.
Реферативно-исследовательская работа по математике:
Тема: "Положительные и отрицательные числа"
Выполнил: Сергеев Александр
ученик 6"А" класса
Руководитель: Терентьева О. А.
учитель математики
пгт Чегдомын
2019г.
Содержание:
Введение 3
1.Основная часть 4
1.1.История возникновения положительных и отрицательных чисел 4-6
1.2.Положительные и отрицательные числа в нашей жизни 6-7
1.3. Развитие идеи отрицательного количества в Европе. 7
1.4.Число как основное понятие математики. 7
1.5.Происхождение символов «плюс» и «минус» 8-9
2.Вывод 10
3.Список литературы 10
Введение:
В начале 6 класса мы приступили к изучению положительных и
отрицательных чисел, еще тогда меня очень заинтересовала эта тема,
но только для изучения.
Мне эти задания, по этой теме, давались очень легко, и меня
заинтересовали возможности данного метода при решении более
сложных заданий.
Вместе с преподавателем мы решили более подробно и тщательно
Изучить данный метод и его возможности, при работе над проектом
по этой теме.
Цель моей работы:
Познакомиться с положительными и отрицательными числами,
Систематизировать знания по данной теме.
Задачи работы:
1. Понять - как работают положительные и отрицательные числа
2.Посмотреть - как нужны в жизни положительные и отрицательные числа
3. Освоение разных методов и методик работы.
4.Обобщение и систематизация знаний по данной теме.
1. Основная часть
1.1 Из истории возникновения положительных и отрицательных чисел:
Люди долго не могли привыкнуть к отрицательным числам.
Отрицательные числа казались им непонятными, ими не
пользовались, просто не видели в них особого смысла. Эти числа
появились значительно позже натуральных чисел и обыкновенных
дробей.
Первые сведения об отрицательных числах встречаются у китайских
математиков во II в. до н. э. и то, были известны лишь правила
сложения и вычитания положительных и отрицательных чисел;
правила умножения и деления не применялись.
Положительные количества в китайской математике называли «чен»,
отрицательные – «фу»; их изображали разными цветами: «чен» -
красным, «фу» - черным. Это можно заметить в книге «Арифметика в
девяти главах» (Автор Чжан Цань). Такой способ изображения
использовался в Китае до середины XII столетия, пока Ли Е не
предложил более удобное обозначение отрицательных чисел – цифры,
которые изображали отрицательные числа, перечеркивали черточкой
наискось справа налево.
Лишь в VII в. индийские математики начали широко
использовать отрицательные числа, но относились к ним с некоторым
недоверием. Бхасхара прямо писал: "Люди не одобряют отвлеченных
отрицательных чисел...". Вот как индийский математик Брахмагупта
излагал правила сложения и вычитания: «имущество и имущество есть
имущество, сумма двух долгов есть долг; сумма имущества и нуля
есть имущество; сумма двух нулей есть нуль… Долг, который
отнимают от нуля, становится имуществом, а имущество – долгом. Если
нужно отнять имущество от долга, а долг от имущества, то берут их
сумму». «Сумма двух имуществ есть имущество».
(+х) + (+у) = +(х + у) (-х) + (-у) = - (х + у)
(-х) + (+у) = - (х - у) (-х) + (+у) = +(у - х)
0 – (-х) = +х 0 – (+х) = -х
Индийцы называли положительные числа «дхана» или «сва»
(имущество), а отрицательные – «рина» или «кшайя» (долг). Индийские
ученые, стараясь найти и в жизни образцы такого вычитания, пришли к
толкованию его с точки зрения торговых расчетов. Если купец имеет
5000 р. и закупает товара на 3000 р., у него остается 5000 - 3000 = 2000, р.
Если же он имеет 3000 р., а закупает на 5000 р., то он остается в долгу
на 2000 р. В соответствии с этим считали, что здесь совершается
вычитание 3000 - 5000, результатом же является число 2000 с точкой
наверху, означающее «две тысячи долга». Толкование это носило
искусственный характер, купец никогда не находил сумму долга
вычитанием 3000 - 5000, а всегда выполнял вычитание 5000 - 3000.
Чуть позже в Древней Индии и Китае догадались вместо слов "долг в 10
юаней" писать просто "10 юаней", но рисовать эти иероглифы черной
тушью. А знаков "+" и "–" в древности не было ни для чисел, ни для
действий.
Греки тоже поначалу знаков не использовали. Древнегреческий ученый
Диофант вообще не признавал отрицательные числа, и если при решении
уравнения получался отрицательные корень, то он отбрасывал его как
"недоступный". И Диофант старался так сформулировать задачи и
составлять уравнения, чтобы избежать отрицательных корней, но вскоре
Диофант Александрийский стал обозначать вычитание знаком.
Правила действий с положительными и отрицательными числами были
предложены уже в III веке в Египте. Введение отрицательных величин
впервые произошло у Диофанта. Он даже использовал специальный символ
для них. В то же время Диофант употребляет такие обороты речи, как
«Прибавим к обеим сторонам отрицательное», и даже формулирует
правило знаков: «Отрицательное, умноженное на отрицательное, дает
положительное, тогда как отрицательное, умноженное на положительное,
дает отрицательное».
В Европе отрицательными числами начали пользоваться с XII–XIII вв., но
до XVI в. большинство ученых считали их «ложными», «мнимыми» или
«абсурдными», в отличие от положительных чисел – “истинных”.
Положительные числа так же толковались как «имущество», а
отрицательные – как «долг», «недостача». Даже знаменитый математик
Блез Паскаль утверждал, что 0 − 4 = 0, так как ничто не может быть
меньше, чем ничто. В Европе к идее отрицательного количества достаточно
близко подошел в начале XIII столетия Леонардо Фибоначчи Пизанский.
На состязании в решении задач с придворными математиками
Фридриха II Леонардо Пизанскому было предложено решить задачу:
требовалось найти капитал нескольких лиц. Фибоначчи получил
отрицательное значение.
"Этот случай, - сказал Фибоначчи, - невозможен, разве только принять,
что один имел не капитал, а долг". Однако в явном виде отрицательные
числа применил впервые в конце XV столетия французский математик
Шюке.
Автор рукописного трактата по арифметике и алгебре «Наука о числах
в трёх частях». Символика Шюке приближается к современной.
Признанию отрицательных чисел способствовали работы французского
математика, физика и философа Рене Декарта. Он предложил
геометрическое истолкование положительных и отрицательных чисел –
ввел координатную прямую. (1637 г.).
Положительные числа изображаются на числовой оси точками, лежащими
вправо от начала 0, отрицательные – влево. Геометрическое истолкование
положительных и отрицательных чисел способствовало к их признанию.
В 1544 году немецкий математик Михаил Штифель впервые
рассматривает отрицательные числа как числа, меньшие нуля
(т. е. « меньшие, чем ничто»). С этого момента отрицательные числа
рассматриваются уже не как долг, а совсем по-новому. Сам Штифель
писал: «Нуль находится между истинными и абсурдными числами…»
Почти одновременно со Штифелем защищал идею отрицательных чисел
Бомбелли Раффаэле (около 1530—1572), итальянский математик и
инженер, переоткрывший сочинение Диофанта.
Так же и Жирар считал отрицательные числа вполне допустимыми и
полезными, в частности, для обозначения недостачи чего-либо.
Всякий физик постоянно имеет дело с числами: он всегда что-то измеряет,
вычисляет, рассчитывает. Везде в его бумагах - числа, числа и числа. Если
приглядеться к записям физика, то обнаружится, что при записи чисел он
часто использует знаки "+" и "-". Например: термометр, шкала глубин и
высот).
Только в начале XIX в. теория отрицательных чисел закончила свое
развитие, и "абсурдные числа" получили всеобщее признание.
1.2 Отрицательные числа в нашей жизни.
Если вы посмотрите на градусник, который измеряет температуру воздуха
на улице,
то увидите, что на его шкале есть отметка «0»,а ниже этой отметки
располагаются
числа со знаком «-» (минус). Вот об этих числах со знаком «минус» мы и
поговорим.
Эти числа называются отрицательными числами.
Необходимость в таких числах возникла давно. В древности индийские
ученые использовали отрицательные числа в торговых расчетах. Если
вы имеете 3000 рублей и покупаете товар на 1000 рублей, то у вас
остается 3000 – 1000 = 2000 рублей. Но если вы имеете 3000 рублей и
покупаете товар на 5000 рублей, то у вас
образуется долг 2000 рублей. Поэтому, в этом случае считали, что
совершается вычитание 3000 – 5000, результатом является число 2000,
означающее «две тысячи долга». Таким образом, – 2000 это
отрицательное число и в данном случае оно
указывает на то, что у вас образовался долг 2000 рублей.
Более современный пример можно привести, используя действия с
телефонным балансом. Если на вашем счету было 200 рублей, а вы
«наговорили» на 300 рублей, то на вашем счету образуется
Отрицательный баланс - 100 рублей (минус 100 рублей).
Это значит, что теперь телефонной компании вы должны 100 рублей.
Первый контакт и изучение отрицательных чисел в системе
образования изучаются в школе, и поэтому мной в школе было
проведено анкетирование «Отношение и понимание отрицательных
чисел» в 5, 9,11 классах и членами математического кружка 3 А
класса. Я получил следующий результат:
Полученные результаты говорят о том, что и в настоящее время к
отрицательным числам проблематичное отношение. Но по мере изучения
отрицательных чисел меняется отношение к ним и уже нет страха перед
операциями с отрицательными числами.
1.3 Развитие идеи отрицательного количества в Европе:
В Европе в XII веке нашей эры появились отрицательные числа, их
называли “ложными” в отличие от положительных чисел – «истинных».
Широко использовать отрицательные числа, выполнять действия с
ними,строить координатную прямую стали благодаря работам
французского математика Декарта. Хотя многие европейские математики
эпохи возрождения так или иначе пользовались отрицательными
числами, их считали «ложными. Но, тем не менее,идея отрицательных
чисел постепенно завоевывала умы и, главное, оказалась весьма полезной.
Выражение «ниже, чем ничего» показывает, что математики мысленно
Воображали положительные и отрицательные числа точками на
вертикальной шкале (вроде шкалы термометра).
Отрицательные числа с большим трудом завоевывали себе место в
математике.
1.4 Число как основное понятие математики.
Число является одним из основных понятий математики. Понятие числа
развивалось в тесной связи с изучением величин; эта связь сохраняется
и теперь. Во всех разделах современной математики приходится
рассматривать разные величины и пользоваться числами. Существует
большое количество определений понятия «число».
Первое научное определение числа дал Эвклид в своих «Началах»:
«Единица есть то, в соответствии с чем каждая из существующих вещей
называется одной. Число есть множество, сложенное из единиц».
Аристотель дал такое определение: «Число есть множество, которое
измеряется с помощью единиц».
Пифагор учил, что «число есть система единиц».
Английский физик и математик Ньютон пишет: «Целое число есть то,
что измеряется единицей»
1.5 Происхождение символов «плюс» и «минус»
Цифры, знаки обозначения арифметических действий и другие
математические символы разрабатывались человечеством постепенно на
протяжении нескольких веков в тесной связи с развитием самой
арифметики. Большинство их образовалось из рисунков, чертежей, букв и
сокращенных слов. До XV в. не было постоянных общепринятых
арифметических знаков.
Символы для арифметических операций сложения «+» и вычитания «-»
встречаются настолько часто, что нынешнее поколение почти не
задумывается об их происхождении. Удивительно, но они появились
вовсе не в глубокой древности. Многое из того, что известно,
происходит из всеобъемлющего и впечатляющего исследования
историка математики Ф.Каджори (автора книги «История
математических обозначений»), которое до сих пор остается
непревзойденным.
Происхождение знаков «+» и «-» точно не известно. Некоторые ученые
считают, что они происходят из торговой средневековой практики от
условных знаков, которые делались на ящиках с товарами, чтобы
отметить избыток или недостаток первоначального веса.
В Древней Греции сложение обозначалось записью рядом, но иногда ее
заменяли символом косой черты «/», а при вычитании - полуэллиптической
кривой. Древние египтяне для обозначения суммирования изображали
пару ног, идущих вперед; обратное же их направление (уход)
символизировало о вычитании.
Термины искомых символов произошли от слов plus – «более», minus –
«менее». Для удобства их использования они были сокращены до первых
букв p и m. В конце XV в. европейские математики Ф.Шике и Л.Пачоли
применяли «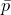
» или «
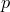», обозначая «плюс» для сложения, и «
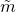» или «
»,
обозначая «минус» для вычитания.
Существует версия, что знак «+» происходит от одной из форм слова «et»
(латин.), означающее «и». Автор книги «Книги неба и мира» астроном
Н.д’Орем в середине XIV в. впервые использовал эту аббревиатуру. Символ
«+» (потомок одной из форм «et») также содержится в рукописи 1417 г.,
однако палочка, направленная сверху вниз, не совсем вертикальна.
Происхождение знака «-» гораздо менее ясно, и высказываются гипотезы
его появления от иероглифического письма или александрийской
грамматики, до черты, которую использовали торговцы, чтобы отделить
тару от общей массы товаров. В Италии ростовщики, давая деньги в долг,
ставили перед именем должника сумму долга и черточку, вроде нашего
минуса, а когда должник возвращал деньги, зачеркивали ее, получалось
что-то вроде нашего плюса.
Первое упоминание современного алгебраического знака «-» относится к
Немецкой рукописи 1481 г., найденная в библиотеке Дрездена.
В латинской рукописи того же времени есть оба символа: «+» и «-».
Изучив эти манускрипты, немецкий математик И.Видман в 1489 г. издал
первую печатную книгу «Коммерческая арифметика», послужившую
руководством по счету для купцов. В этой книге автор использовал оба
знака «+» и «-», что указывает на возможность их происхождения из
торговли. В Италии исследуемые символы были приняты астрономом
К.Клавиусом, математиками Глориози и Б.Кавальери в начале XVII в. .
Чуть позднее, в 1544 г. немецкий ученый М.Штифель выпустил «Полную
Арифметику», где встречаются такие записи для чисел: 0-2; 0-5; 0+2; 0+7.
Числа первого вида названы им «меньше, чем ничего», второго вида –
«больше, чем ничего». Первое употребление «+» и «-» на английском языке
обнаружено в книге по алгебре 1551 г. математика из Оксфорда Р.Рекорда:
«Часто используются другие два знака, первый из которых пишется «+» и
обозначает больше, а второй «-» и обозначает меньше».
Однако даже после принятия знака «+» не все использовали этот символ.
И.Видман ввел его как греческий крест «+» (современный знак),
горизонтальная черта которого немного длиннее вертикальной. Такие
математики, Р.Рекорд, Харриот и Р.Декарт, охотно использовали такой же
знак. Другие (например, Юм, Гюйгенс, и Ферма) употребляли латинский
крест «†», иногда расположенный горизонтально, с перекладиной на одном
конце или на другом. Наконец, Галлей использовал более декоративный
вид «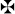
». Обозначения вычитания были менее затейливыми, однако
немного запутанными: вместо привычного нам и простого знака «-» в
немецких, швейцарских и голландских книгах применяли символ «÷»,
которым ныне обозначается деление. Возможно, это было сделано для
того, чтобы не смешать знак «минус» со знаком препинания («тире»). Этот
знак встречается и в «Арифметике» Л.Ф. Магнитского. В некоторых
книгах XVII в. (например, у Р.Декарта и Мерсенна) для изображения
вычитания использованы две точки «∙∙» или три точки «∙∙∙».
Изобретение математических знаков облегчило изучение математики и
способствовало дальнейшему ее развитию. Впечатляюще, что символы,
появившиеся впервые в печати лишь около 500 лет назад, стали
наиболее универсальным «языком»
2. Вывод:
В ходе работы я узнал, что отрицательные и положительные числа
играют важную роль в жизни людей, они помогают смотреть на то, что ты
должен, что тебе должны, они важны как и в жизни, так и в задачах, и
примерах.
Работая с различными источниками и исследуя различные явления, и
процессы, мы выяснили, что отрицательные и положительные числа
используются в медицине, физике, географии, истории, в современных
средствах связи, при изучении качеств человека и других сферах
деятельности. Данная тема является актуальной и находит широкое
применение, и активно используются человеком.
Польза отрицательных чисел в науке и жизни человека разнообразна
и велика. Понять суть отрицательных чисел без истории их возникновения
немыслимо. Работая с литературными источниками, установлено, что
положительные и отрицательные числа служат для описания изменений
величин.
3. Список литературы:
1.Учебник Математика 6 класс С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин (2012 год)
2.Источники из интернета.
3. Ф.Каджори (автора книги «История математических обозначений»)
20
