Рабочая тетрадь для студентов "Производная"

Тема: Производная

Составитель:

Мусихина В.Г., преподаватель математики БПОУ УР «Увинский профессиональный колледж»

Пояснительная записка.

Рабочая тетрадь по математике для студентов 1 курса БПОУ УР «УПК» составлена в соответствии с действующими рабочими программами и может быть использована для самостоятельной работы учащимися, а также для выполнения домашних работ. Тетрадь содержит задачи репродуктивного, поискового характера, а так же имеется ряд задач повышенной сложности, решение которых требует определенных умений и навыков, которые могут служить базой для дальнейшего изучения курса математики.

Содержание

1. Определение производной

2. Основные правила дифференцирования

3. Упражнения на закрепление изученных понятий

4. Производные тригонометрических функций

5. Проверочная работа

6. Геометрический смысл производной

7. Физический смысл производной

8. Производная сложной функции

9. Письменная работа

Производной функции у=f(х) в точке х₀ называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю у^'= lim f(х₀+Δx)-f(х₀).

Δx

Нахождение производной данной функции у=f(х) называется дифференцированием.

Основные правила дифференцирования

1. a′=0

2. x′=1

3. (ax)′=a

4. (xⁿ)′=nxⁿˉ¹

5. (u+v)′=u′+v′

6. (uv)′=u′v+uv′

7. (u/v)′=(u′v-v′u)/v²

1. a′=0. Производная от числа равна нулю.

7′=0; (1⁄3)′=0; (-2,5)′=0; (√11)′=0

4′ =_____; (-15)′ =______; (7,81)′ = ______;

(√2)′=_______ (5/7)′ =______.

2. x′=1. Производная от любой переменной равна

единице.

у′ =________________; в′=_____________

3. (ax)′=a. Постоянный множитель можно выносить

за знак производной.

(13х)′=13; (¶х)′= ¶; (-¼х) ′ = -¼; (√2х)′ = √2

(101х)′ = __________

(-56х)′ = __________

(⅞х) ′ = __________

(√8х) ′ = _________

4. (xⁿ)′=n·xⁿˉ¹

(х⁶)′=6х⁵; (3х⁴)′ = 3·4х³ = 12х³;

(-¼х⁴)′ =-¼·4 х³=- х³

(Х²¹)' = _______________

(10х⁴)' = _______________

(-⅓х³)' = _______________

(Х^1/2)' = _______________

5. (u+v)′=u′+v′

(3х+5)'=(3х)'+5'=3+0=3

(5х²+8х-10)'=(5х²)'+(8х)'-10'=5·2х+8-0=10х+8

(х⁴-х⁹)'= (х⁴)' – (х⁹)'= 4х³ – 9х⁸

(3х² – 6х)' = _______________________________________________________

(х³+ 4х¹⁰⁰-1)' = _____________________________________________________

(3х⁴-7х³+2х²+¶)'=___________________________________________________

6. (u·v)′=u′·v+u·v′

1. (х(х+3))' = х'·(х+3) + х· (х+3)'= 1·( х+3) + х · 1=х+3+х=2х+3

2. ((х²-х)(5х-8))'= (х²-х)'·(5х-8) + (х²-х)·(5х-8)'=(2х-1)(5х-8)+

+(х²-х)5= 10х²-21х+8+5х²-5х= 15х²-26х+8

((х+5)(х+7))'=___________________________________________________________

_______________________________________________________________________

((х²-2)(х⁷+4))'=__________________________________________________________

_______________________________________________________________________

7. (u/v)′=(u′·v-v′·u)/v²

(х²/(х+3))'= ((х²)'·(х+3) - х²·(х+3)')/(х+3)²=

=(2х(х+3)-х²)/(х+3)²=(2х²+6х-х²) /(х+3)²=(х²+6х) /(х+3)²

((3х)/(2х-1))'=__________________________________________________________

______________________________________________________________________

((6х-9)/(-11х+7))'= ______________________________________________________

_______________________________________________________________________

Проверь себя

«3»	«4»	«5»
(4х2 – Зх)'=____________ _____________________ (2х3-3х2+5х+15)'=_______ ______________________ ______________________ (2х(х2+6))'=____________ ______________________ ______________________ ((3х+5)/(8х4))'=_________ ______________________ ______________________ ______________________	(12х3 -бх2)'=____________ ______________________ (5х4+3х3-4х2+х8)'=_______ _______________________ _______________________ ((7х+3)(8х4))'=__________ ______________________ ______________________ ((3х3-8)/(2х+4))'= ______________________ ______________________ ______________________ _______________________	(¼х4√3х2+х)'=___________ ______________________ (⅞x8+⅓x3-⅟2x2+x8)'= ______________________ ______________________ _______________________ ((3х2-5х+1)(2х+9))'= ______________________ ______________________ ______________________ ((7х2-3х+4)/(5х+3))'= ______________________ ______________________ _______________________ _______________________

Производные тригонометрических

функций

• (sinx)′=cosx

• (cosx)′=-sinx

• (tgx)′=1/cos²x

• (ctgx)′=-1/sin²x

(2sinx)′=2cosx; (x+2cosx)′=1-2sinx;

(1/2tgx)′=1/2cos²x; (сosx-tgx)′=-sinx-1/cos²x

(2tgx-sinx)′=2/cos²x-cosx

(tgx+11) '= _____________________________________________________________

(cosx- sinx) '=___________________________________________________________

(5sinx+2х) '= ___________________________________________________________

(Ctgx+2х³) '= ___________________________________________________________

(2sinx+ cosx-3)'= ________________________________________________________

(tgx +3 cosx)'= __________________________________________________________

(-sinx+х³) '= ____________________________________________________________

(2cosx-5х⁴+2х+1) '= ______________________________________________________

Установи соответствие

(2sinx+3)'

(4 cosx+х²)'

(tgx+7)'

(ctgx+3х²+8)'

(7 sinx-1/7)'

(tgx+ 2sinx)'

((tgx)/3)'

(√3 cosx-х⁵+0,3х)'

(3 cosx+15х)'

(sinx/ cosx)'

-√3 sinx-5х⁴+0,3

1⁄3 cos ²x

-3 sinx+15

-1⁄sin ²x +6х

1⁄ 2sinx ²x +6

-4 sinx+2х

1⁄cos ²x

3cosx

2⁄ cos ²x +6

7 cosx

1 ⁄ cos ²x+2 cosx

15+ cosx

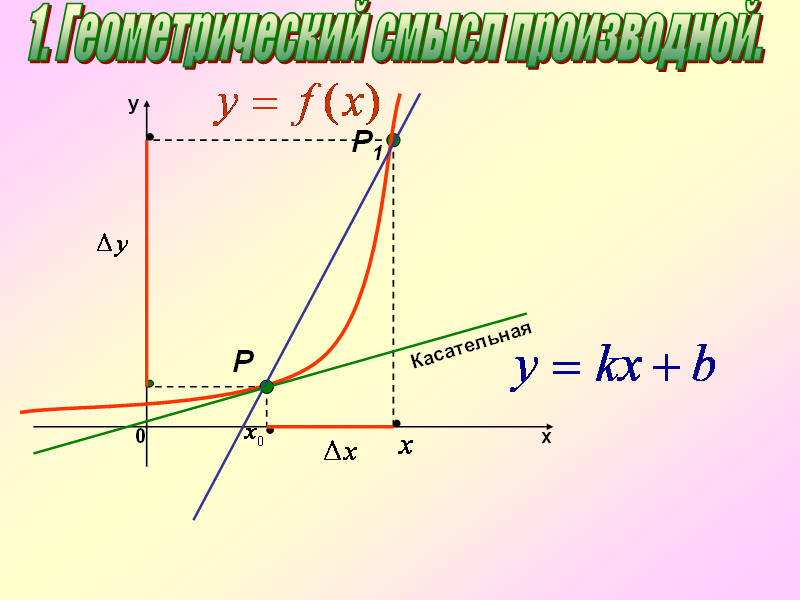
Производная в точке х₀ равна угловому коэффициенту касательной к графику функций у=f(х) в этой точке.

К = угловой коэффициент, равный тангенсу угла прямой с осью ОХ

К= f '(х₀)= tgα.

у=у(х₀)+у'(х₀)(х-х₀) - уравнение касательной

1.Найдем угловой коэффициент касательной к графику функции у=f(х) в точке с абсциссой (х₀):

Решение: f(х) =х², х₀=-4

К= f '(х₀); f '(х)=2х; f '(х₀)= f '(-4)=2·(-4)=-8, т.е. к=-8

1. f(х)=1⁄х, в х₀=- 1⁄3 ______________________________________________

________________________________________________________________

1. f(х)= sinx, в х₀ = ¶⁄3_____________________________________________

______________________________________________________________

1. f(х)= 3х³ – 2х +1, в х₀₌1__________________________________________

________________________________________________________________

2. Найдем тангенс угла касательной к кривой у=1⁄2 х² с осью Ох, в точке х₀=1.

Решение: tgα=у'(х₀); у'(х)=( 1⁄2 х²)'=х; у'(х₀)= у'(1)=1, т.е. tgα=1; α=¶⁄4

1. у= х² при х₀=√3⁄2________________________________________________

_______________________________________________________________________

2. f(х)=1⁄3 х³, х₀=1 ________________________________________________

_______________________________________________________________________

3. Найдем уравнение касательной к графику функции у=1⁄3 х²-2в точке с абсциссой х₀₌3.

Решение: Находим уравнение касательной у=у(х₀)+у'(х₀)(х-х₀)

у(х₀)=у(3)= 1⁄3 ·3²-2=1; у'(х)= (1⁄3 х²-2)'=2⁄3 х; у'(х₀)= у'(3)= 2⁄3 ·3= 2

у=1+2(х-3)=1+2х-6=2х-5; т.е. у=2х-5 – уравнение касательной

1. f(х)=3х²-5х+4, в х₀=1____________________________________________

______________________________________________________________________

______________________________________________________________________

1. у=1⁄2 х²+1, в х₀=2_______________________________________________

______________________________________________________________________

______________________________________________________________________

Если точка движется вдоль оси Ох и ее координата изменяется по закону х(t), то мгновенная скорость точки V(t)=х'(t)

V=S' (t), а ускорение а (t)= V' (t)=х'' (t)= S'' (t)

Тело движется по закону S (t)=3t²-5t+8. Найдем скорость и ускорение движения тела и вычислить их значения при t=1.

Решение: V (t)= S' (t)= 6 t-5; V (1)=6·1-5=1

а= V'(t)=( 6 t-5)'=6

Ответ: V=1, а=6

1. Определить скорость и ускорение тела, движущегося по закону S(t)= t²+2 в момент времени t=5: _____________________________

______________________________________________________________

______________________________________________________________

_______________________________________________________________________

1. Определить скорость и ускорение тела, движущегося по закону S(t)= 0,5t³+2t²-7t+11 в момент времени t=2:

______________________________________________________________

_______________________________________________________________________

_______________________________________________________________________

Если функция f имеет производную в точке х, а функция g имеет производную в точке у=f(х), то сложная функция h(x)=g(f(x)) также имеет производную в точке х:

h′(x)=g′(f(x))·f′(x)

Найдем производную сложной функции:

1.((2х+3)¹°°)′=2·100(2х+3)⁹⁹=200(2х+3)⁹⁹

2.(√3х²+1)′=(1/2·(3х²+1))·(3х²+1)′=6х/(2·√3х²+1)=3х/√3х²+1

1. у =(4х-9)⁷ _________________________________________________________

_______________________________________________________________________

1. у = (х⁄3 +2)¹²_______________________________________________________

_______________________________________________________________________

1. у = (7-24х)¹⁰ _______________________________________________________

_______________________________________________________________________

1. у = cosx(5х-9)_______________________________________________

_______________________________________________________________________

1. у= sinx(7-2х) ______________________________________________

_______________________________________________________________________

1.Производная функции у=f(х) в точке х₀ называется предел _________________

__________________, когда приращение аргумента стремится к нулю.

2.Функцию, имеющую производную в точке х₀ называют____________________

_________________ в этой точке.

3.Найти производные функций:

3.1 у=х³+√2____________________________________________________________

3.2 у=3х⁴-7х³-х+¶_______________________________________________________

3.3 у=7х³-5х___________________________________________________________

3.4 у=х-х³+7___________________________________________________________

3.5 у=(5х-2)·(4х-1)______________________________________________________

______________________________________________________________________

3.6 у=(5х+2)⁄(4х-1)_____________________________________________________

______________________________________________________________________

3.7 у=(7х+5)·(8х-4)_____________________________________________________

______________________________________________________________________

3.8 у=(3х²-8)/(2х-4)_____________________________________________________

______________________________________________________________________

3.9 у=3cosх____________________________________________________________

3.10 у=sin2х___________________________________________________________

3.11 у=1/2 sinх-х⁵_______________________________________________________

3.12 у=5tgх____________________________________________________________

3.13 у= tg3х____________________________________________________________

3.14 у=3cosх+2_________________________________________________________

______________________________________________________________________

3.15 у=2х⁵-3cosх________________________________________________________

_______________________________________________________________________

4. Найти угловой коэффициент касательной в точке с абсциссой х₀:

4.1 у=7х³-21х²+18, при х₀=1______________________________________________

_______________________________________________________________________

4.2 у=х³-2х²+3х-6, при х₀=-1______________________________________________

_______________________________________________________________________

4.3 у=sinx+cosx, при х₀=¶⁄2________________________________________________

_______________________________________________________________________

4.4 у=х²⁄2+х, при х₀=1____________________________________________________

_________________________________________

5.Пусть S, пройденный телом за время t, выражается формулой. Определить скорость тела V. Вычислить значение скорости при определенном значении t.

5.1 S(t)=2х³-5х²+11х-3, при t=2___________________________________________

_______________________________________________________________________

_______________________________________________________________________

5.2 S(t)=5,5t²-8t+11, при t=2_______________________________________________

_______________________________________________________________________

5.3 S(t)=t²+2, при t=10___________________________________________________

_______________________________________________________________________

6. Найти угол, образованный касательной к графику функции в точке х₀:

6.1 у=х⁶-4х, при х₀=1_____________________________________________________

_______________________________________________________________________

6.2 f(х)= -х⁵-2х²+2, при х₀=-1______________________________________________

_______________________________________________________________________

6.3 f(х)=10-cosх, при х₀=3¶⁄2_______________________________________________

6.4 f(х)=2tgх, при х₀=¶⁄4___________________________________________________

_______________________________________________________________________

7.Найти уравнение касательной к графику функции в точке с абсциссой х₀:

7.1 у=-1⁄3 х²+4, при х₀=3_________________________________________________

_______________________________________________________________________

7.2 у=1⁄6 х²+х-3, при х₀=3_________________________________________________

_______________________________________________________________________

7.3 у=х³-6х²+5, при х₀=1_________________________________________________

_______________________________________________________________________

7.4 у=х-х²+3, при х₀=2___________________________________________________

_______________________________________________________________________

Критерий оценки: «3» - выполнить 16заданий

«4» - выполнить 24 задания

«5» - выполнить более 24 заданий

МАТЕМАТИКА - во всем, нам твердят

Многие не верят, спорить норовят

Математика от нас далеко,

Жить на свете без нее так легко.

Но однажды вечером пойдет дождь,

Подойдешь к окну и поймешь:

Все на свете что нам дано

Математикой предопределено.

Прямоугольники, квадраты и круги

Пространства времени

Неслышные шаги.

Все движется, все уплывает вдаль,

А кто не видит этого,

Того мне просто жаль.

21