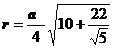Департамент образования мэрии города Новосибирска
Дворец творчества детей и учащейся молодежи «Юниор»
XXXIX городская открытая научно-практическая
конференция НОУ «Сибирь»
Секция: математические модели
Тема: Звёздчатые формы додекаэдров
Автор: Гольцова Мария
МБОУ ЭКЛ, 9 класс
Центральный округ г. Новосибирска
Научный руководитель: Кривченкова
Татьяна Владимировна,
учитель математики в.к.к.
МБОУ ЭКЛ
Контактный телефон: 89139568347
Новосибирск, 2019
Оглавление
Введение…………………………………………………………………………3
Основная часть
Определение додекаэдра и его свойства………………………………...4
История появления додекаэдра…………………………………………..5
Звёздчатые формы додекаэдров………………………………………….6
Звездчатые многогранники ………………………………………………7
Практическая часть…………………………………………………………….9
Заключение……………………………………………………………………..11
Список литературы……………………………………………………………12
Приложение…………………………………………………………………….13
Вдохновение нужно в геометрии не
меньше, чем в поэзии. (А.С. Пушкин)
Введение
В кабинете математики в шкафу я увидела замысловатую объёмную фигуру, которую раньше нигде не встречала. Поинтересовавшись у учителя, я узнала, что это многогранник, а точнее правильный, который называется додекаэдром. Мне захотелось подробнее узнать об этой фигуре. Так я впервые столкнулось с темой «Правильные многогранники».
Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. Человек проявляет интерес к правильным многогранникам на протяжении всей своей сознательной деятельности. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие – в виде вирусов, которые можно рассмотреть с помощью электронного микроскопа.
Чем привлекательны многогранники? Они обладают богатой историей, которая связана с такими знаменитыми учеными древности, как Платон, Евклид, Архимед, Кеплер. Все они использовали в своих философских теориях правильные многогранники. Прошли века, но роль геометрии не изменилась.
Поэтому мне захотелось больше узнать о многогранниках и самой научиться изготавливать модели различных многогранников. Данная тема актуальна, так как немногие люди знают правильные многогранники, но знание этих геометрических тел поможет в создании различных шедевров (как в архитектуре, так и в живописи и во многом другом, потому что многогранники имеют обширную область применения).
Из информации в интернете я узнала, что существует много разных додекаэдров с множеством интересных свойств. Особенно мне понравился додекаэдр, который имел звёздчатые формы, мне захотелось изготовить модели этих фигур.
Цель проекта:
Задачи проекта:
Собрать информацию по данной теме.
Познакомиться с понятием “додекаэдр”.
Узнать о его звёздчатых формах.
Изготовить модели додекаэдра и звёздчатых додекаэдров.
Методы исследования: сбор информации, обработка данных, сравнение, анализ, обобщение.
Определение додекаэдра и его свойства
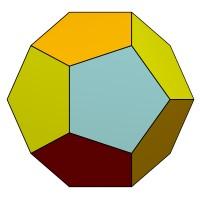
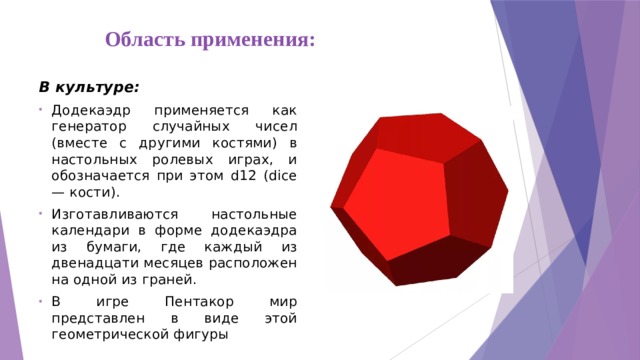
Додекаэдр (от греческого dodeka –двенадцать и hedra – грань) это правильный многогранник, составленный из двенадцати равносторонних пятиугольников. Додекаэдр имеет 20 вершин и 30 ребер.
Вершина додекаэдра является вершиной трех пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°. Если принять длину ребра за а, то получим следующие формулы:
| Сумма ребер | 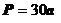
|
| Площадь поверхности | 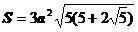
|
| Объем | 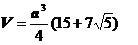
|
| Радиус описанной сферы | 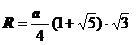
|
| Радиус вписанной сферы | 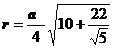
|
|
|
|
|
|
|
Свойства додекаэдра:
Двугранный угол между любыми двумя смежными гранями додекаэдра равен ≈116°,565.
Сумма плоских углов при каждой из 20 вершин равна 324°.
В додекаэдр можно вписать куб так, что стороны куба будут диагоналями додекаэдра.
Додекаэдр имеет три звёздчатые формы.
В додекаэдр можно вписать пять кубов. Если заменить пятиугольные грани додекаэдра плоскими пятиугольными звездами так, что исчезнут все ребра додекаэдра, то получим пространство пяти пересекающихся кубов. Додекаэдр как таковой исчезнет. Вместо замкнутого многогранника появится открытая геометрическая система пяти ортогональностей. Или симметричное пересечение пяти трехмерных пространств.
Ближайшая параллельная к произвольно выбранной грани плоскость, в которой лежат пять вершин, не принадлежащих выбранной грани, отстоит от этой грани на расстояние радиуса описанной вокруг данной грани окружности. А радиус описанной вокруг этих пяти вершин окружности равен диаметру вписанной в любую из граней окружности.
Область применения:
В культуре:
Додекаэдр применяется как генератор случайных чисел (вместе с другими костями) в настольных ролевых играх, и обозначается при этом d12 (dice — кости).
Изготавливаются настольные календари в форме додекаэдра из бумаги, где каждый из двенадцати месяцев расположен на одной из граней.
В игре Пентакор мир представлен в виде этой геометрической фигуры.
История появления додекаэдра
Считается что, самый древний предмет в форме додекаэдра был найден в северной Италии, около Падуи, в конце XIX века, он датируется 500 г. до н. э. и предположительно использовался этрусками в качестве игральной кости.
 Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различные классические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Евклид в предложении 17 книги XIIIв. «Начал» строит додекаэдр на рёбрах куба. Папп Александрийский в «Математическом собрании» занимается построением додекаэдра, вписанного в данную сферу, попутно доказывая, что вершины додекаэдра лежат в параллельных плоскостях.
Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различные классические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца». Евклид в предложении 17 книги XIIIв. «Начал» строит додекаэдр на рёбрах куба. Папп Александрийский в «Математическом собрании» занимается построением додекаэдра, вписанного в данную сферу, попутно доказывая, что вершины додекаэдра лежат в параллельных плоскостях.
На территории нескольких европейских стран найдено множество предметов, называемых римскими додекаэдрами, относящихся ко II—III вв. н. э., назначение которых не совсем понятно.
Римский додекаэдр — это небольшой объект, сделанный из бронзы или реже из камня или железа, чаще имеющий форму додекаэдра с двенадцатью плоскими пятиугольными гранями. Римский додекаэдр датируется II—III веком н. э.
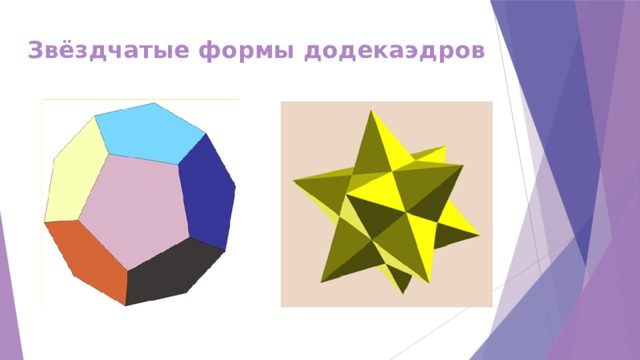
Звёздчатые формы додекаэдра:
Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Они называются также телами Кеплера- Пуансо.
Додекаэдр имеет 3 звёздчатые формы:
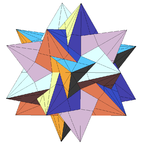
 малый звёздчатый додекаэдр - он считается первой звёздчатой формой додекаэдра. Это тело Кеплера — Пуансо. Многограннику дал имя Артур Кэли. Малый звёздчатый додекаэдр является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 граней в виде пентаграмм с пятью пентаграммами, сходящимися в каждой вершине.
малый звёздчатый додекаэдр - он считается первой звёздчатой формой додекаэдра. Это тело Кеплера — Пуансо. Многограннику дал имя Артур Кэли. Малый звёздчатый додекаэдр является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 граней в виде пентаграмм с пятью пентаграммами, сходящимися в каждой вершине.
Он имеет то же самое расположение вершин, что и выпуклый правильный икосаэдр. Кроме того, у него то же самое расположение рёбер, что и у большого икосаэдра.
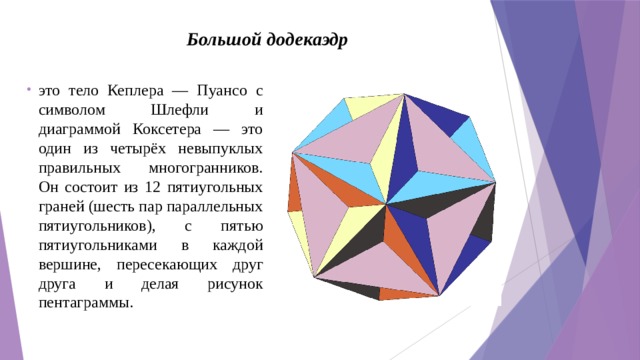
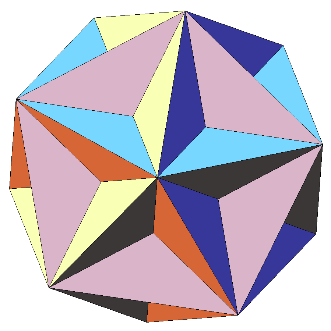 большой додекаэдр - это тело Кеплера — Пуансо с символом Шлефли {5,5/2} и диаграммой Коксетера — это один из четырёх невыпуклых правильных многогранников. Он состоит из 12 пятиугольных граней (шесть пар параллельных пятиугольников), с пятью пятиугольниками в каждой вершине, пересекающих друг друга и делая рисунок пентаграммы.
большой додекаэдр - это тело Кеплера — Пуансо с символом Шлефли {5,5/2} и диаграммой Коксетера — это один из четырёх невыпуклых правильных многогранников. Он состоит из 12 пятиугольных граней (шесть пар параллельных пятиугольников), с пятью пятиугольниками в каждой вершине, пересекающих друг друга и делая рисунок пентаграммы.
 большой звёздчатый додекаэдр - является одним из четырех правильных звёздчатых многогранников тел Кеплера-Пуансо. Гранью многогранника является правильный звёздчатый многоугольник, который состоит из правильных треугольников.
большой звёздчатый додекаэдр - является одним из четырех правильных звёздчатых многогранников тел Кеплера-Пуансо. Гранью многогранника является правильный звёздчатый многоугольник, который состоит из правильных треугольников.
В отличие от октаэдра, любая из звёздчатых форм додекаэдра не является соединением Платоновых тел, а образует новый многогранник. У большого додекаэдра гранями являются пятиугольники, которые сходятся по пять в каждой из вершин. У малого звёздчатого и большого звёздчатого додекаэдров грани — пятиконечные звёзды (пентаграммы), которые в первом случае сходятся по 5, а во втором по 3 грани в одной вершине. Вершины большого звёздчатого додекаэдра совпадают с вершинами описанного додекаэдра.
Звездчатые многогранники:
Ещё существуют такие звездчатые многогранники:
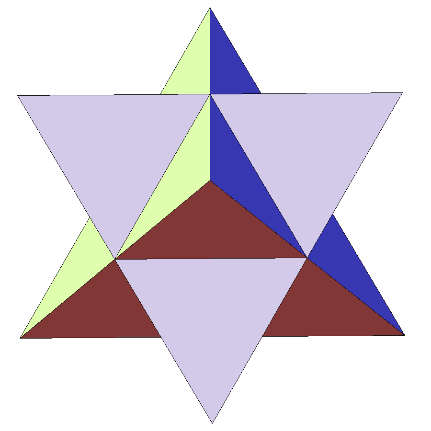 Звёздчатый октаэдр
Звёздчатый октаэдр
Существует только одна звёздчатая форма октаэдра. Звёздчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт И. Кеплером и назван им Stella octangula — звезда восьмиугольная. Отсюда эта форма имеет и второе название: «stella octangula Кеплера»; по сути она является соединением двух тетраэдров.
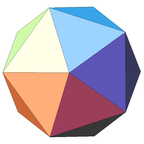 Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 — неполной икосаэдральной симметрией, что было доказано Коксетером совместно с Дювалем, Флэзером и Петри c применением правил ограничения, установленных Дж. Миллером. Одна из этих звёздчатых форм, называемая большим икосаэдром, является одним из четырёх правильных звёздчатых многогранников Кеплера — Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.
Икосаэдр имеет 59 звёздчатых форм, из которых 32 обладают полной, а 27 — неполной икосаэдральной симметрией, что было доказано Коксетером совместно с Дювалем, Флэзером и Петри c применением правил ограничения, установленных Дж. Миллером. Одна из этих звёздчатых форм, называемая большим икосаэдром, является одним из четырёх правильных звёздчатых многогранников Кеплера — Пуансо. Его гранями являются правильные треугольники, которые сходятся в каждой вершине по пять; это свойство является у большого икосаэдра общим с икосаэдром.
Среди звёздчатых форм также имеются: соединение пяти октаэдров, соединение пяти тетраэдров, соединение десяти тетраэдров. Первая звёздчатая форма — малый триамбический икосаэдр.
Если каждую из граней продолжить неограниченно, то тело будет окружено большим многообразием отсеков — частей пространства, ограниченных плоскостями граней. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства 20 + 30 + 60 + 20 + 60 + 120 + 12 + 30 + 60 + 60 = 472 отсека десяти различных форм и размеров. Большой икосаэдр состоит из всех этих кусков, за исключением последних шестидесяти. Следующая звёздчатая форма — завершающая.
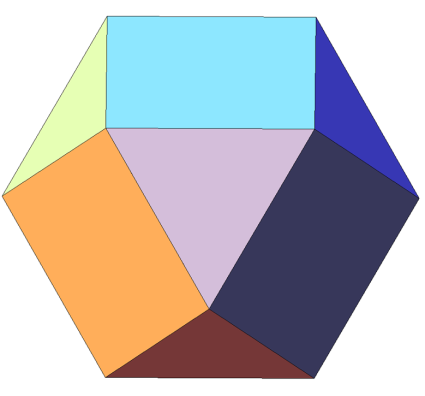 Звёздчатые формы кубооктаэдра- полуправильный многогранник, состоящий из 14 граней (8 правильных треугольников и 6 квадратов). В кубооктаэдре 12 одинаковых вершин, в которых сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат. Икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 — правильными треугольниками.
Звёздчатые формы кубооктаэдра- полуправильный многогранник, состоящий из 14 граней (8 правильных треугольников и 6 квадратов). В кубооктаэдре 12 одинаковых вершин, в которых сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат. Икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 — правильными треугольниками.
 Икосододекаэдр имеет множество звёздчатых форм, первая из которых есть соединение икосаэдра и додекаэдра.
Икосододекаэдр имеет множество звёздчатых форм, первая из которых есть соединение икосаэдра и додекаэдра.
Звёздчатые формы икосододекаэдра- икосододекаэдр имеет 32 грани, из которых 12 являются правильными пятиугольными гранями, а остальные 20 — правильными треугольниками.
Икосододекаэдр имеет множество звёздчатых форм, первая из которых есть соединение икосаэдра и додекаэдра.
Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр. Звездчатый октаэдр был открыт Леонардо да Винчи, затем спустя почти 100 лет переоткрыт Иоганном Кеплером, и назван им Stella octangula звезда восьмиугольная. Отсюда октаэдр имеет и второе название «stella octangula Кеплера».
Практическая часть

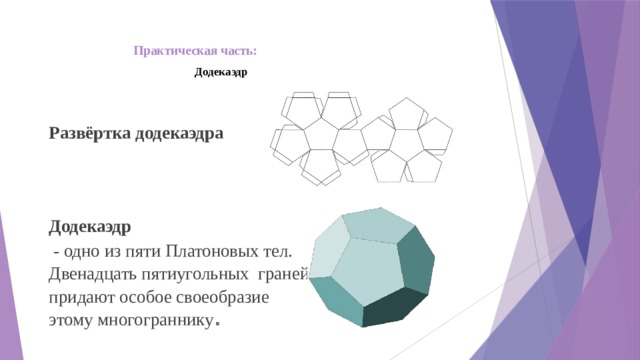
Додекаэдр
Развёртка додекаэдра
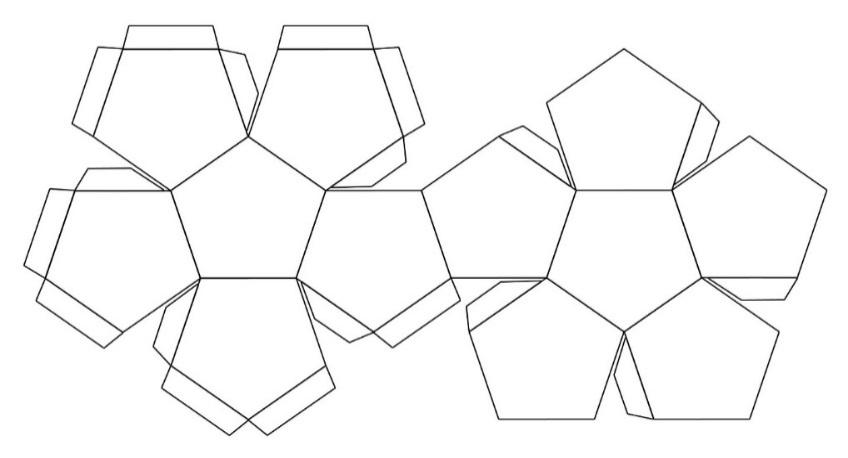
Додекаэдр - одно из пяти Платоновых тел. Двенадцать пятиугольных граней придают особое своеобразие этому многограннику. Я изготовила календарь в форме додекаэдра. (Приложение)
Звёздчатый додекаэдр (малый)
Чтобы изготовить модель звёздчатого додекаэдра, надо привести его к этой форме. Под приведением к звёздчатой форме понимается процесс построения многогранника из другого многогранника путём расширения его граней. Для этого через грани исходного многогранника проводятся плоскости и рассматриваются всевозможные рёбра, полученные в результате пересечения этих плоскостей и выбираются подходящие.

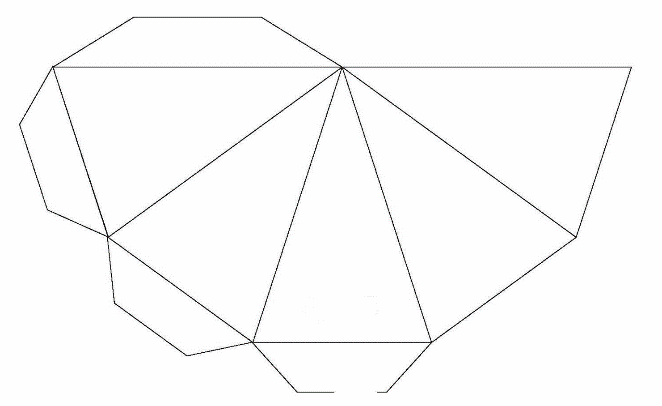
Развёртка пирамиды, таких нужно сделать 12 штук. Двенадцать пирамид, надстроенных над каждой из граней исходного додекаэдра, создают пространственную 3D-звезду - первую звездчатую форму додекаэдра. Другое название - малый звездчатый додекаэдр. (Приложение)
 Звёздчатый додекаэдр (большой)
Звёздчатый додекаэдр (большой)
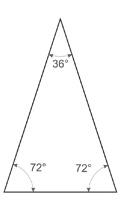
Гранью многогранника является правильный звёздчатый многоугольник, который состоит из правильных треугольников. Форма грани имеет следующий вид:
Многогранник состоит из 60-ти треугольных граней.
Для того, чтобы создать большой звёздчатый додекаэдр нужно сделать развёртку икосаэдра, он будет основой, затем делаем 20 тетраэдров, рассчитывая размер длины его граней так: длину ребра икосаэдра делим на 2, и делим на косинус 72х градусов(~0.309).
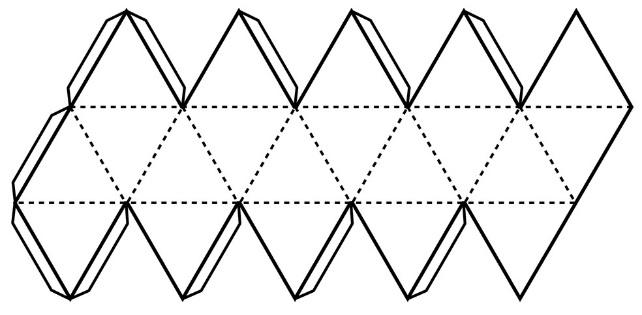
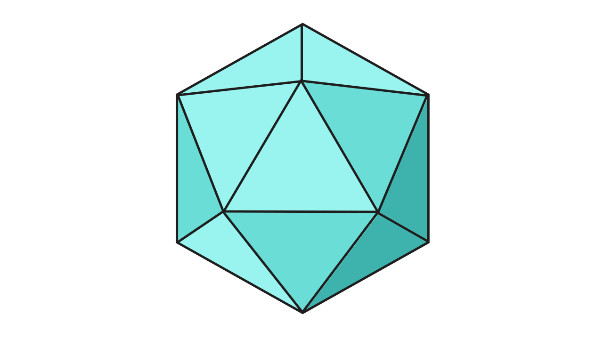 Развёртка икосаэдра
Развёртка икосаэдра
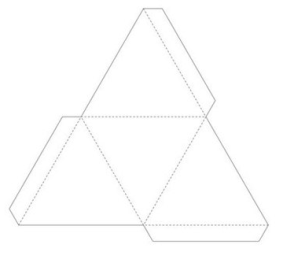
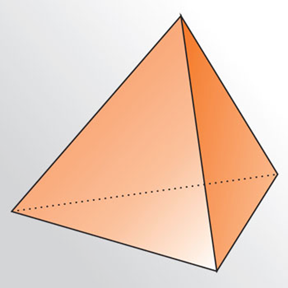 Развертка тетраэдра
Развертка тетраэдра

Звёздчатый додекаэдр (большой)
Заключение
В ходе работы я изучила информацию, представленную в интернете. Я узнала, что существует большое множество различных звёздчатых многогранников. Собрала информацию по данной теме, познакомилась с понятием додекаэдр, узнавла о его звёздчатых формах и изготовила модели додекаэдра и малого звёздчатого додекаэдра. Исходя из всего выше изложенного, я считаю, что достигла поставленой цели, а также выполнила все задачи. Считаю свою работу интересной, полезной и содержательной. При работе над проектом, я получила бесценный опыт: узнать что-то новое, ранее незнакомое. Я получила огромное удовольствие от проделанной мною работы. Моя работа может быть использованы на уроках геометрии, на различных конкурсах и как иллюстративный материал, может помочь расширить знания ребят по теме «Многогранники». Этим проектом хотелось бы расширить представления о мире многогранников и доказать, что многогранники - слагаемые прекрасного.
Также рекомендую ознакомиться со своей работой тем сверстникам, которые хотят знать о математике больше, чем рядовой школьник.
Литература и интернет-ресурсы
М. Веннинджер Модели многогранников. — М.: Мир, 1974.
Гончар В. В. Модели многогранников. — М.: Аким, 1997.
https://ru.wikipedia.org/wiki/Звёздчатый_многогранник
https://ru.wikipedia.org/wiki/Большой_звёздчатый_додекаэдр
https://ru.wikipedia.org/wiki/Кубооктаэдр
https://mnogogranniki.ru/bolshoj-zvjozdchatyj-dodekaedr.html?lang=ru-RU
https://ru.wikipedia.org/wiki/Большой_додекаэдр
https://ru.wikipedia.org/wiki/Малый_звёздчатый_додекаэдр
http://www.myshared.ru/slide/276140/
http://bushmelev.ru/poly/item/135-dodecahedr3forms.html
https://pikabu.ru/story/malyiy_zvyozdchatyiy_dodekayedr_iz_kartona_6480611
Приложение