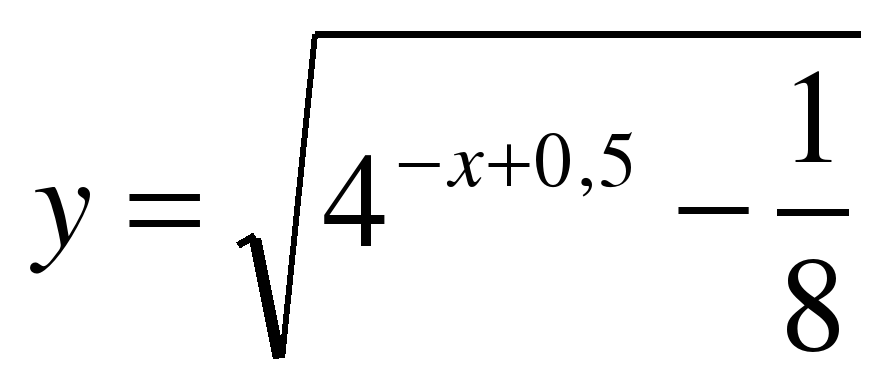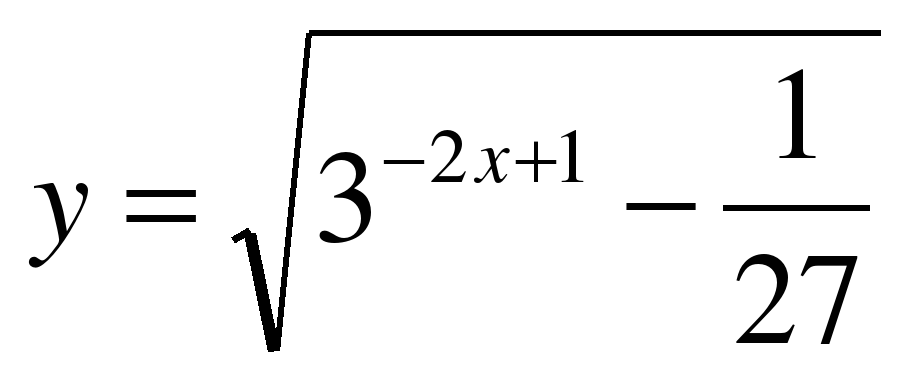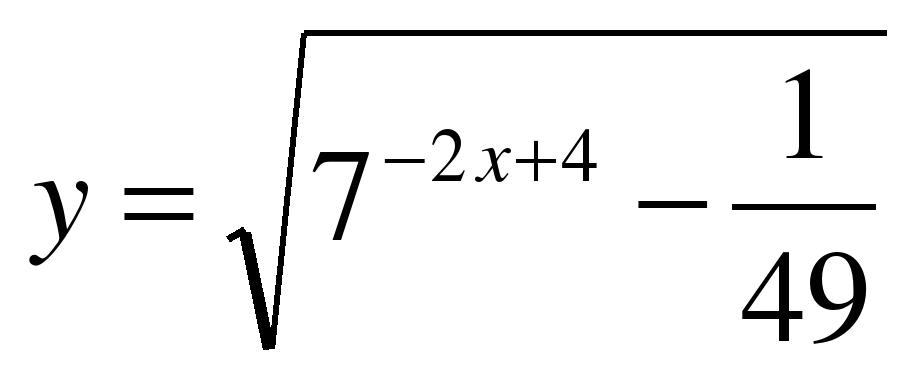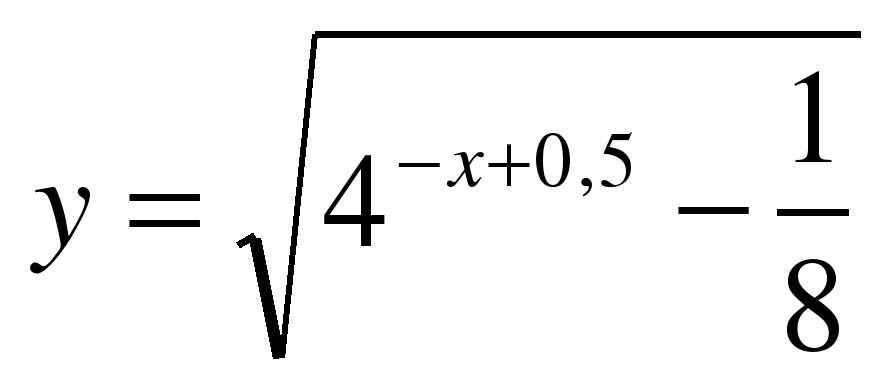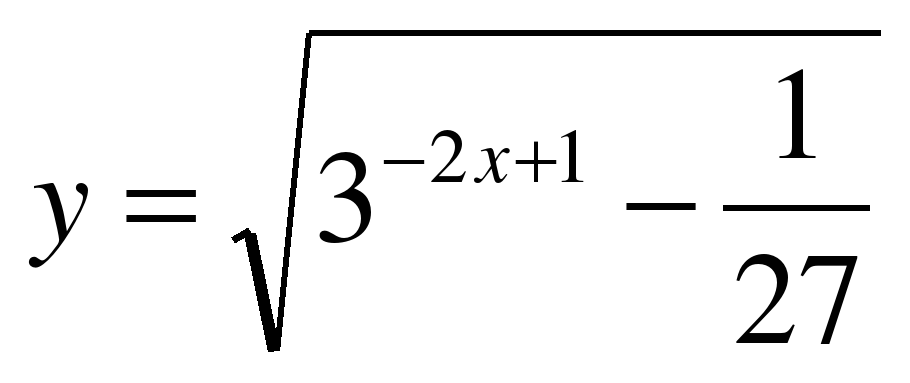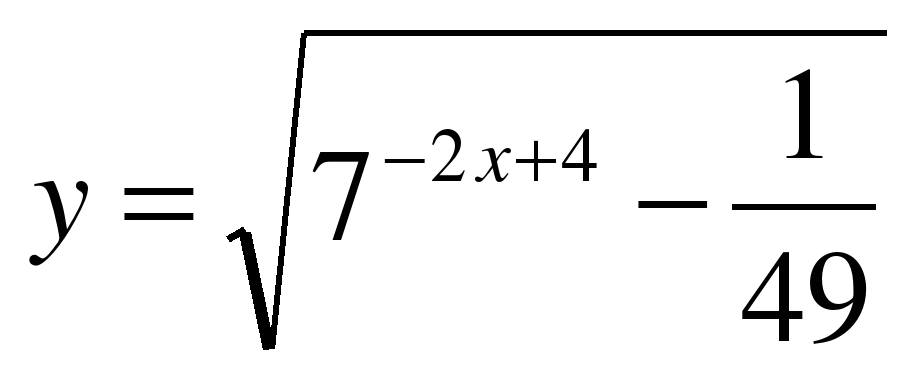Комплект содержит 10 различных вариантов для подготовки к ЕГЭ по математике. Также в набор входят ответы к первой части
Просмотр содержимого документа
«Математика_10вариант»
ЕГЭ по МАТЕМАТИКЕ
Вариант № 10
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается
4 часа (240 мин). Работа состоит из трех частей и содержит 26 заданий.
Часть 1 содержит 13 заданий (А1 – А10 и В1 – В3) обязательного уровня по материалу курса «Алгебра и начала анализа» 10-11 классов.
К каждому заданию А1 – А10 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ.
Часть 2 содержит 10 более сложных заданий (В4 – В11, С1, С2) по материалу курса «Алгебра и начала анализа» 10-11 классов, а также различных разделов курсов алгебры и геометрии основной и средней школы. К заданиям В4 – В11 надо дать краткий ответ, к заданиям С1 и С2 – записать решение.
Часть 3 содержит 3 самых сложных задания, два – алгебраических
(С3, С5) и одно – геометрическое (С4). При их выполнении надо записать обоснованное решение.
.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха!
ЧАСТЬ 1
| При выполнении заданий А1 – А10 в бланке ответов № 1 под номером выполняемого задания поставьте знак "´" в клеточке, номер которой соответствует номеру выбранного вами ответа. |
| A1
| Найдите значение выражения ��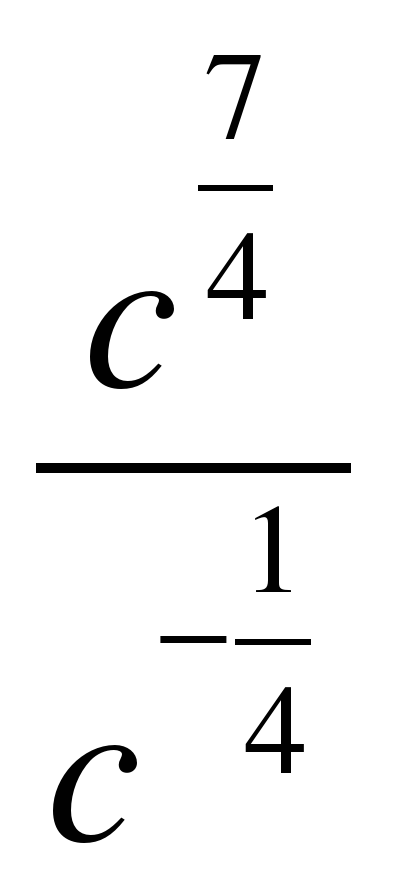 при с = 3 при с = 3 1) 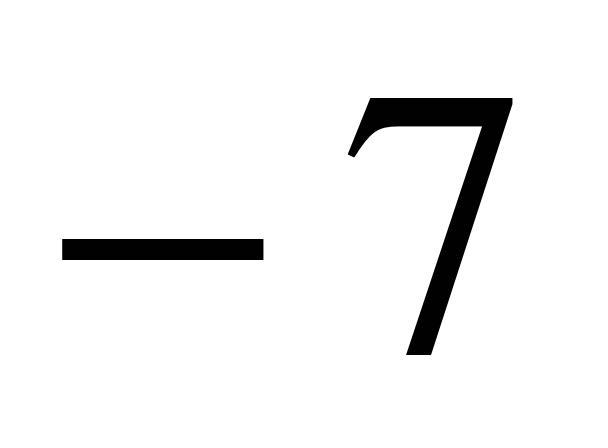 2) 9�� 3) �� 2) 9�� 3) ��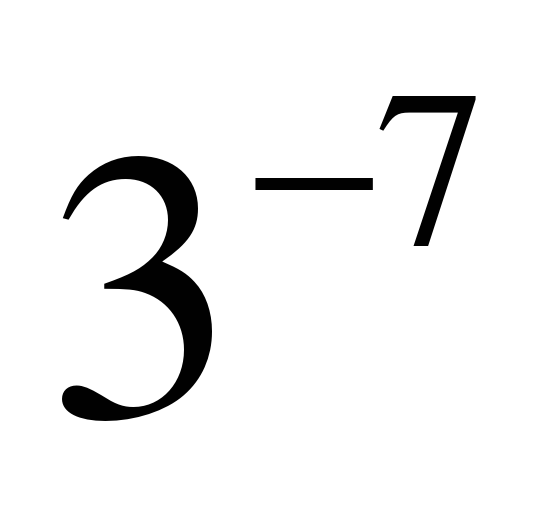 4)�� 4)�� 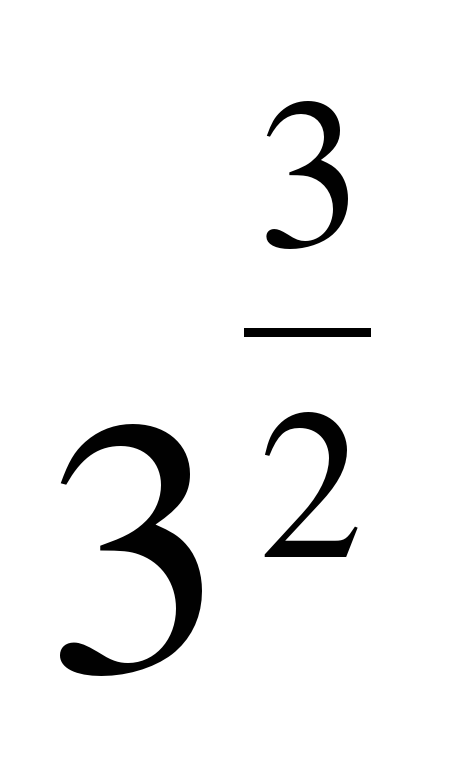 . .
|
|
|
|
| A2
| Вычислите: ��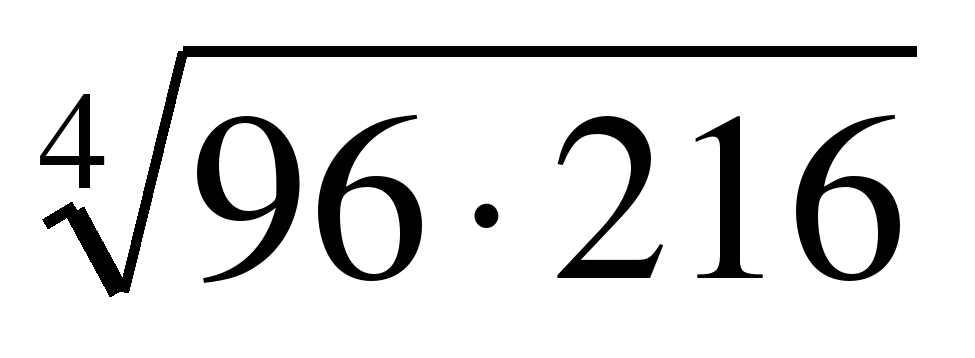 1) 12 2) 144 3) 72 4) 24 |
|
|
|
| A3
| Вычислите: �� 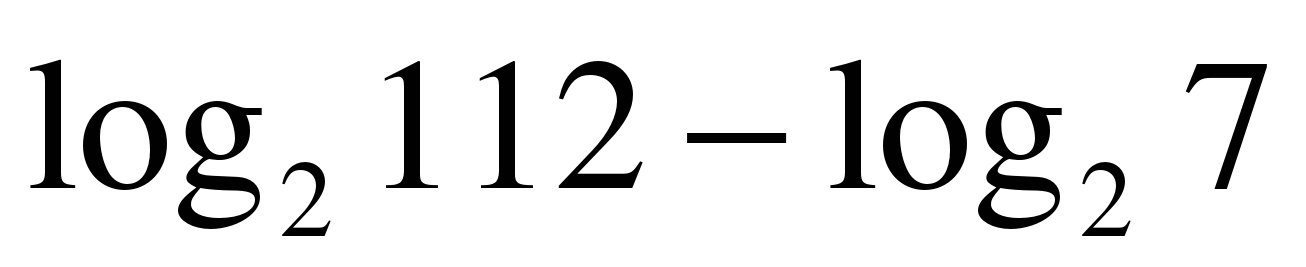 1) 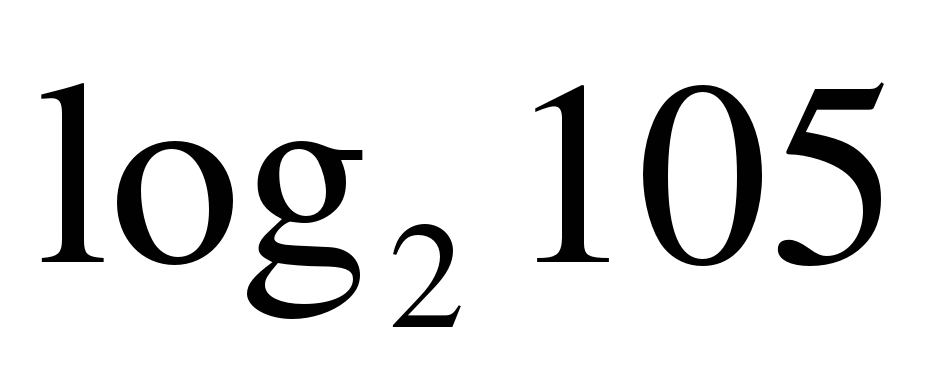 2) 16 3) 8 4) 4�� 2) 16 3) 8 4) 4�� |
|
|
|
| A4
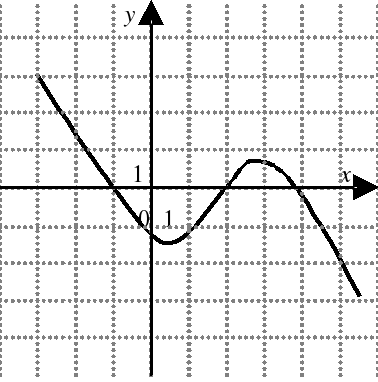
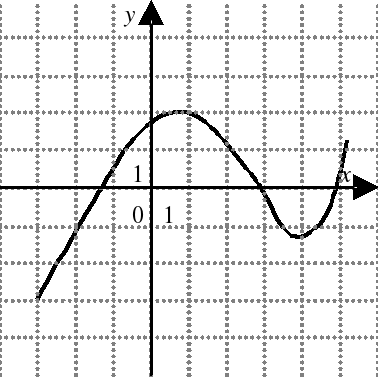
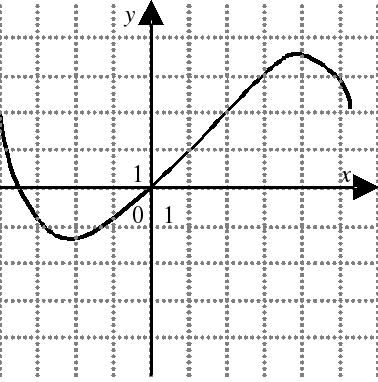
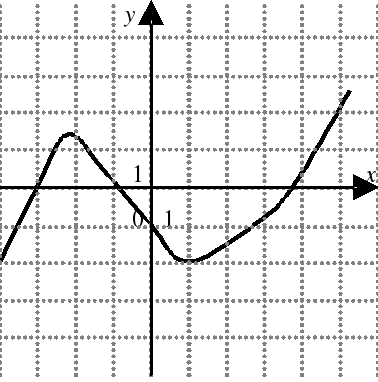
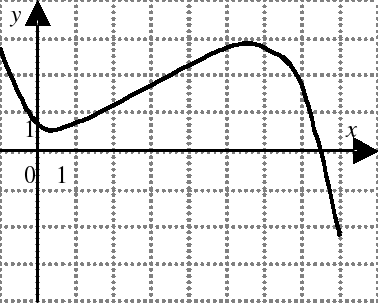
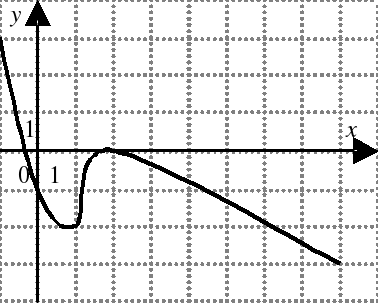
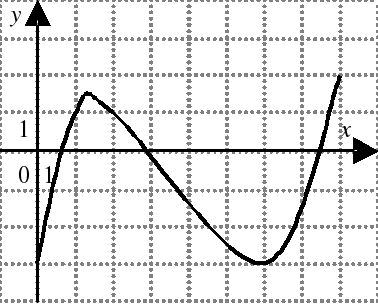
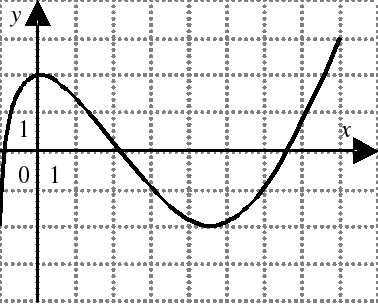
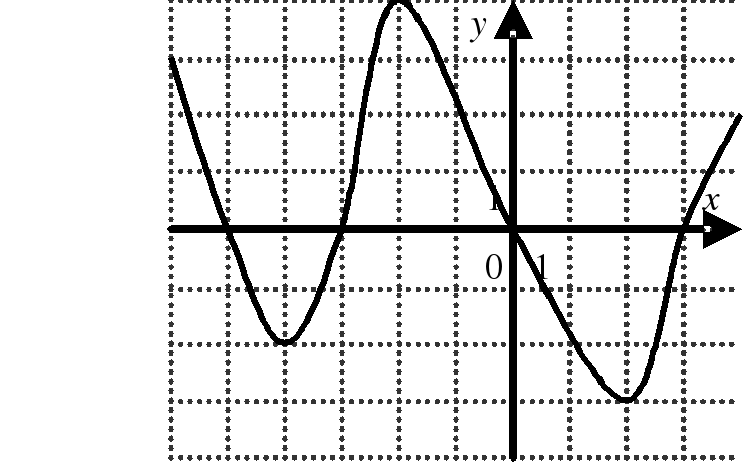
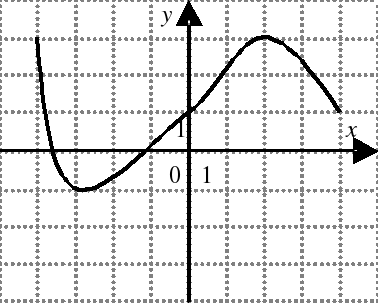
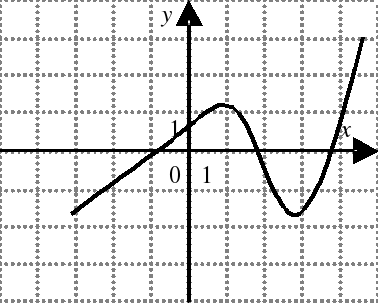
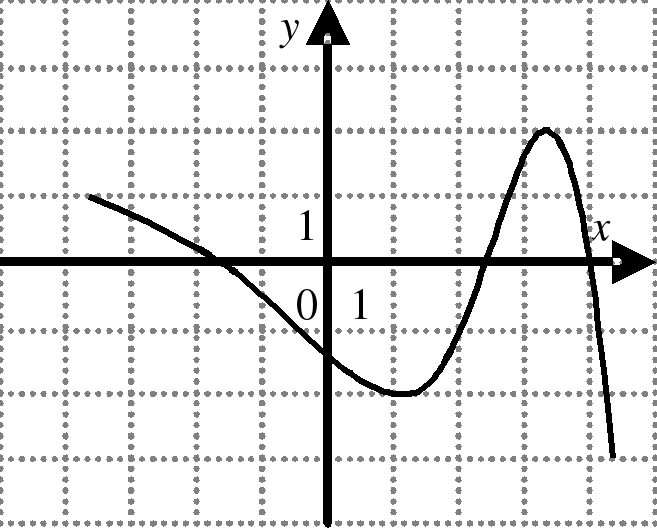
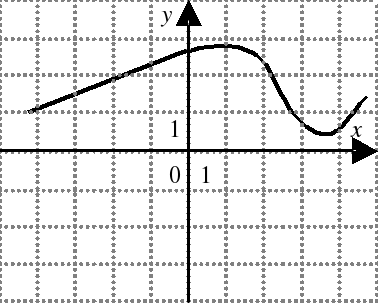
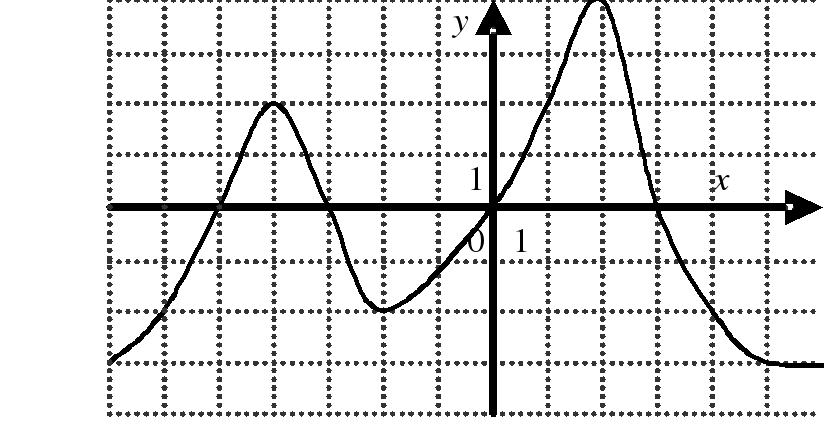
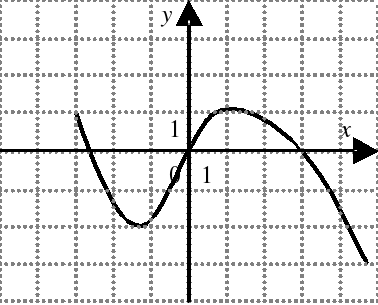
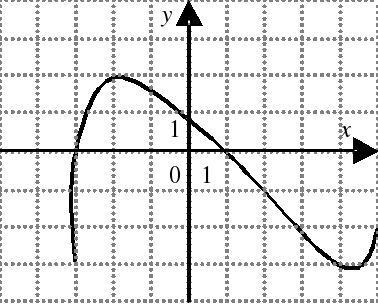
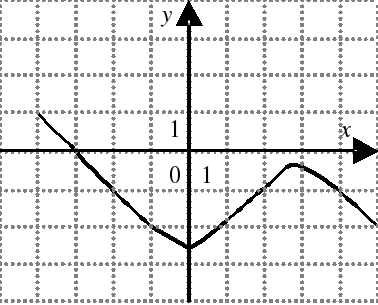
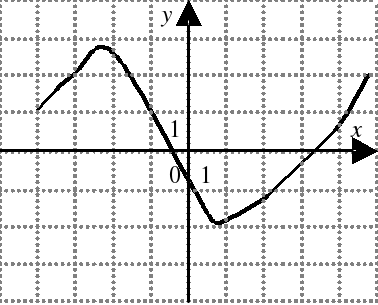
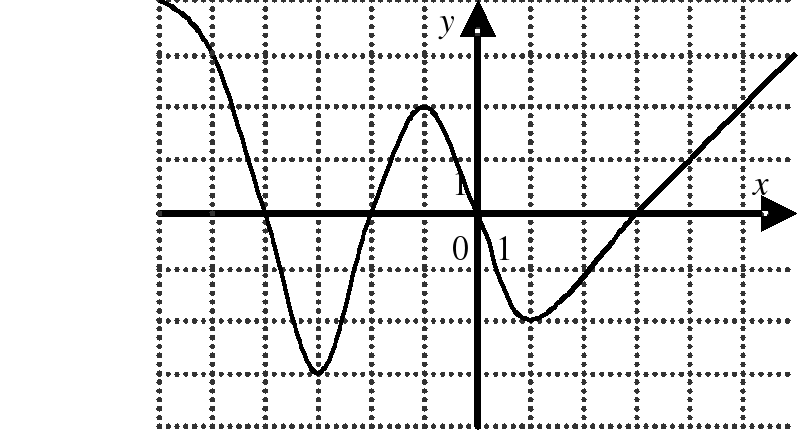
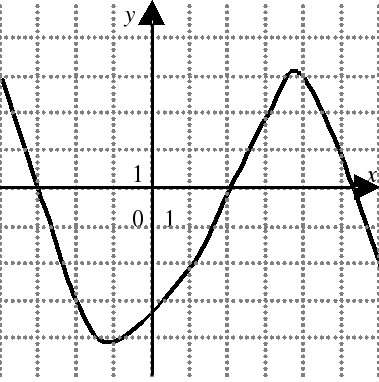
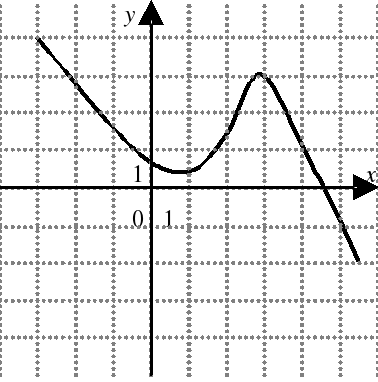
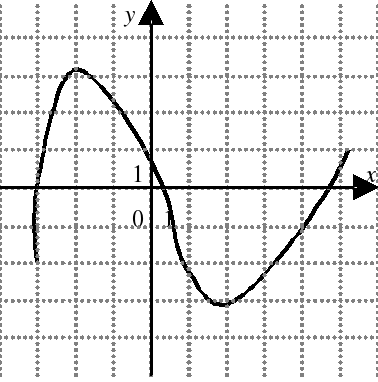
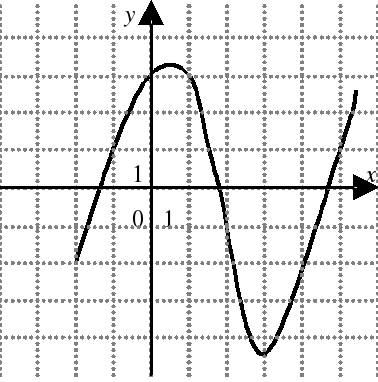
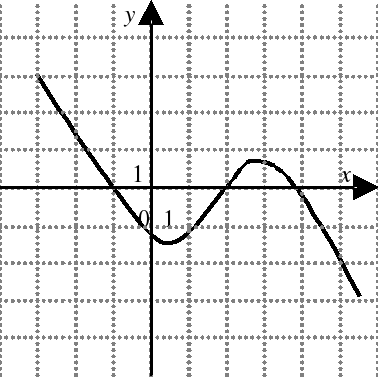
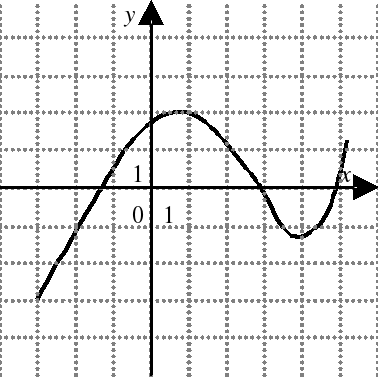
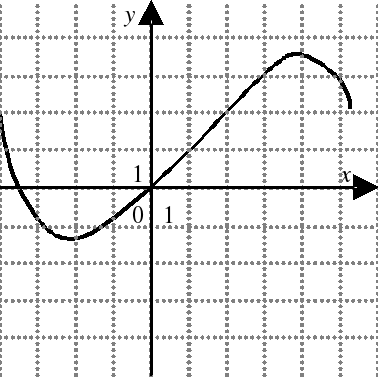
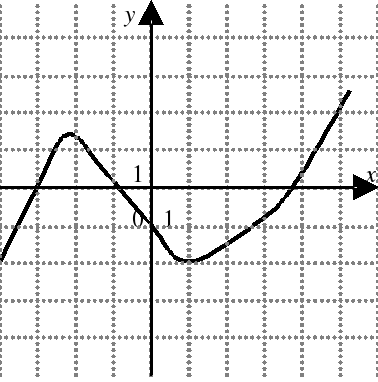
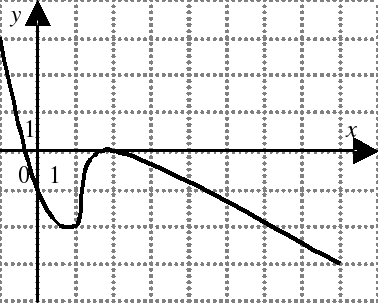
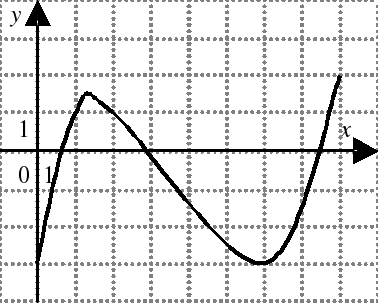
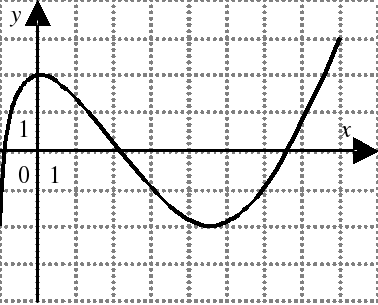
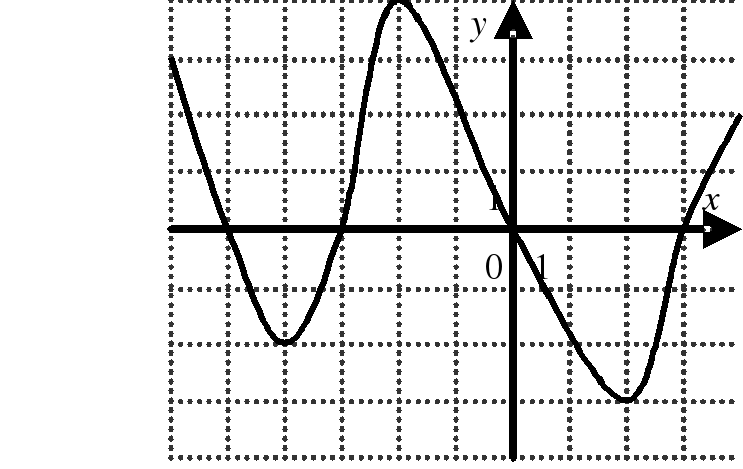
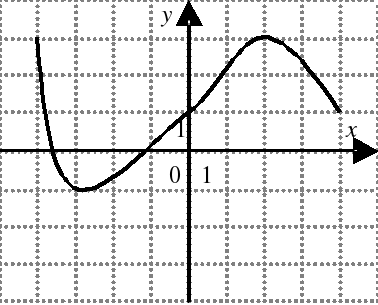
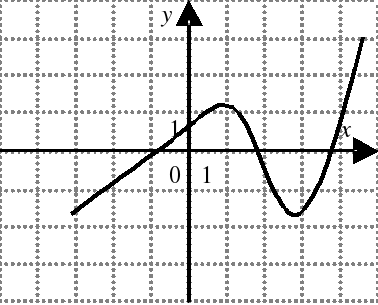
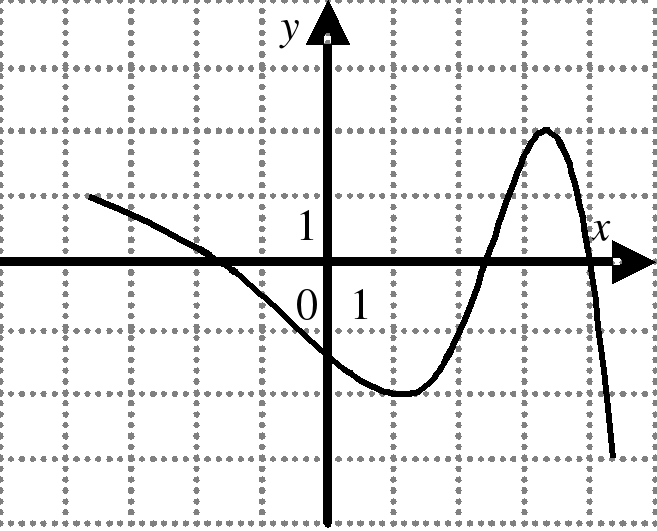
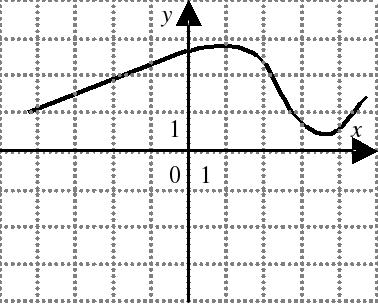
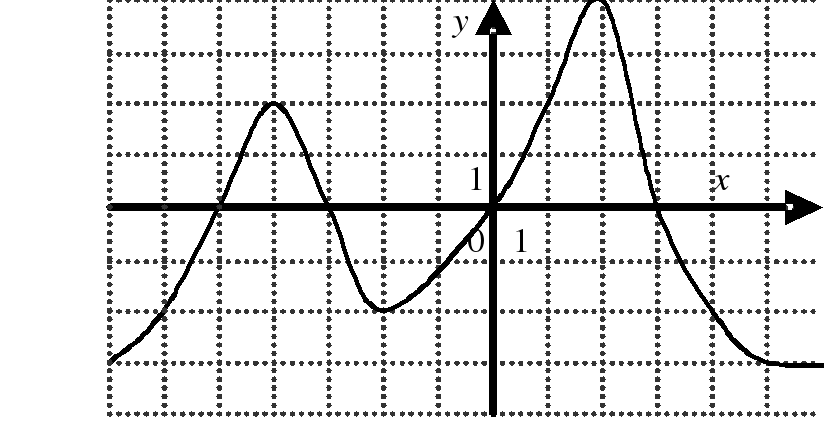
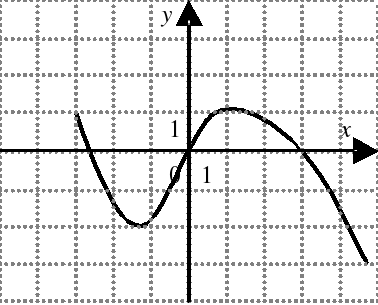
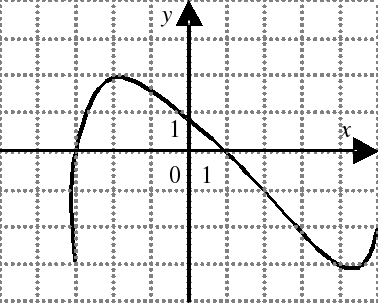
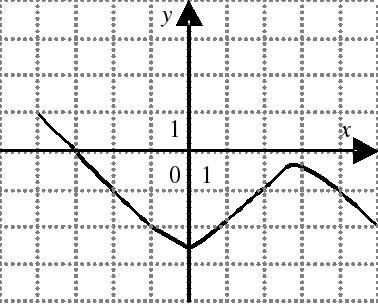
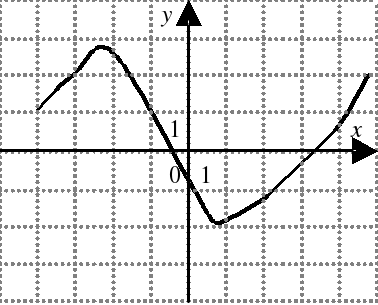
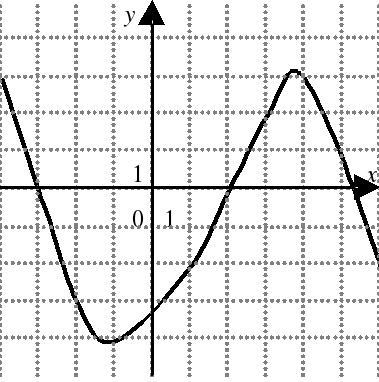
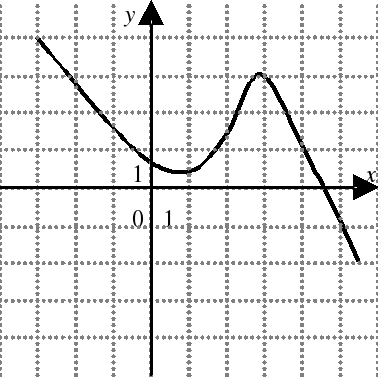
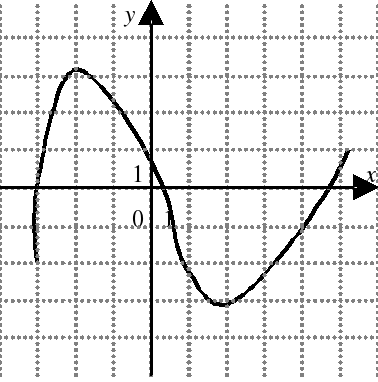
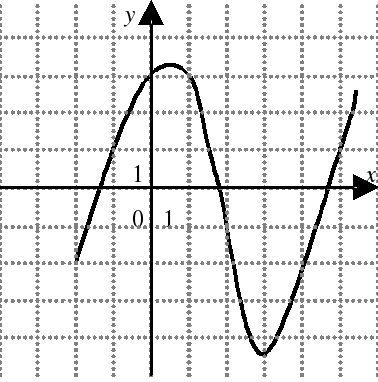
| На каком из следующих рисунков функция, заданная графиком, возрастает на промежутке [0;3] ?
|
|
| Найдите производную функции �� 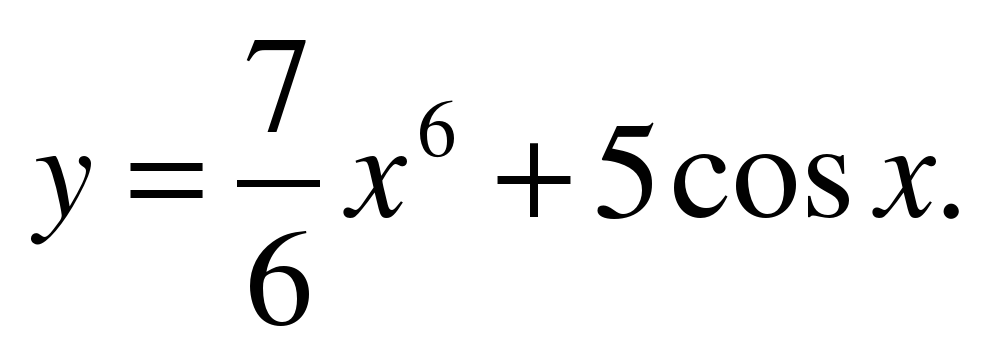 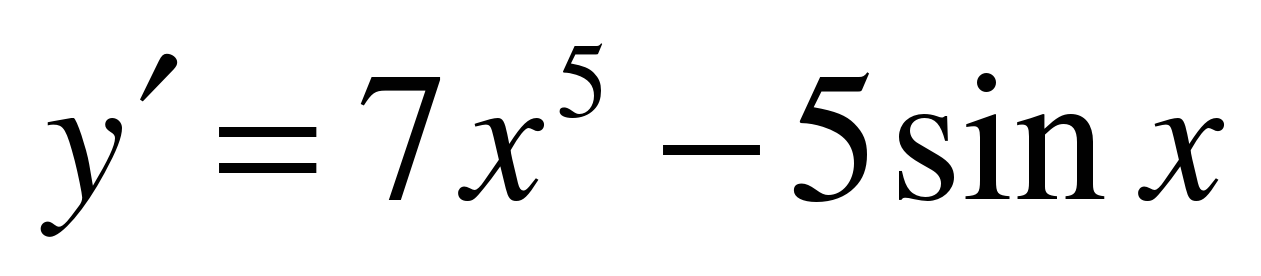 �� 3) �� 3) 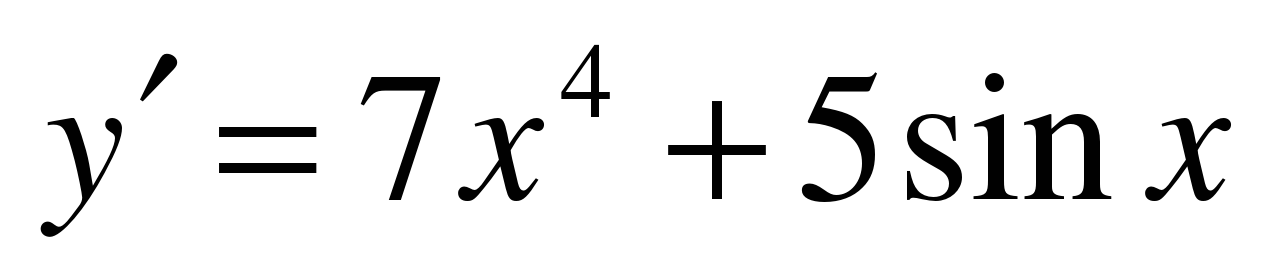 �� �� 2) ��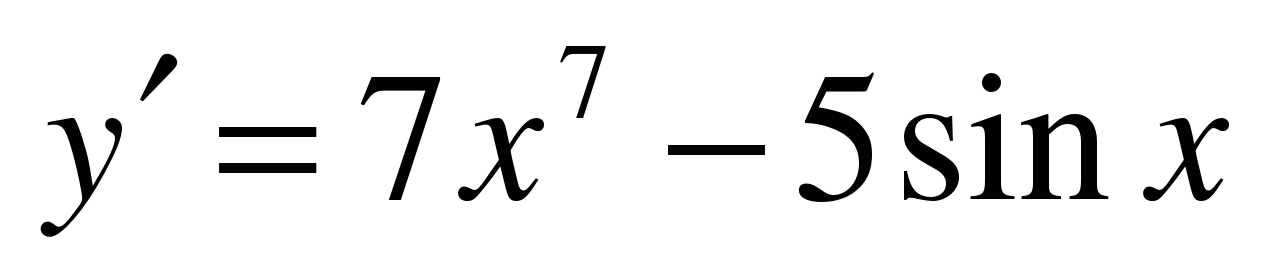 4) �� 4) ��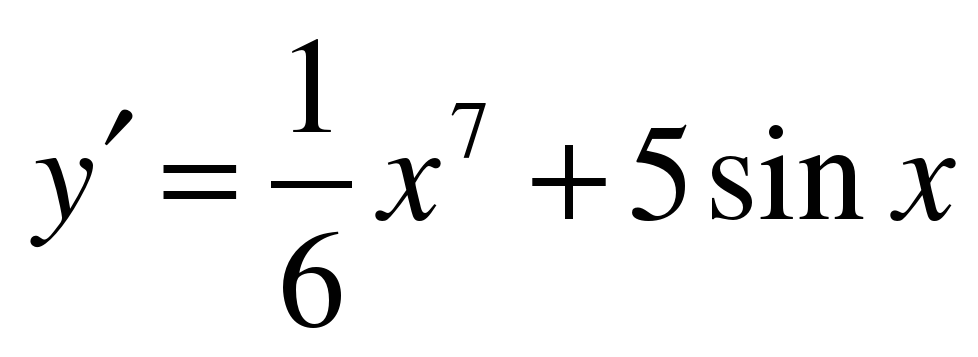
|
|
|
|
| A6 A7 A5
| Найдите множество значений функции �� 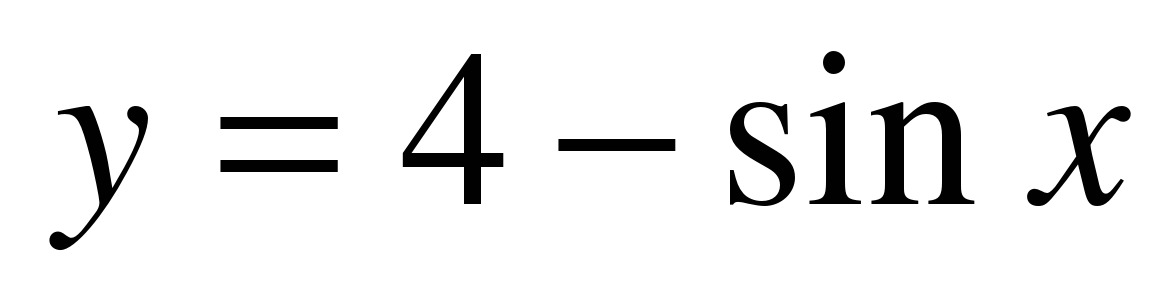 . . 1) 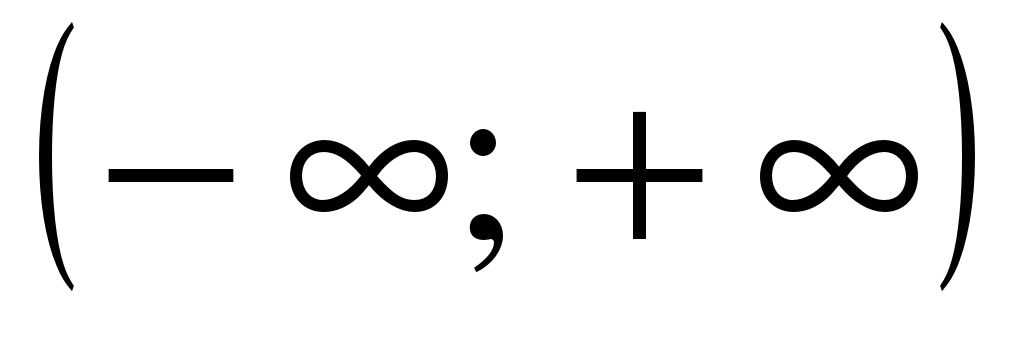 2) [–1; 1] 3) [3; 5]�� 4) [3; 4]. 2) [–1; 1] 3) [3; 5]�� 4) [3; 4].
|
|
|
|
|
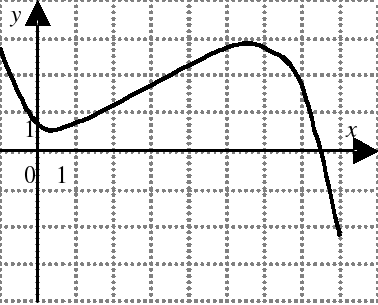
| | Решите неравенство 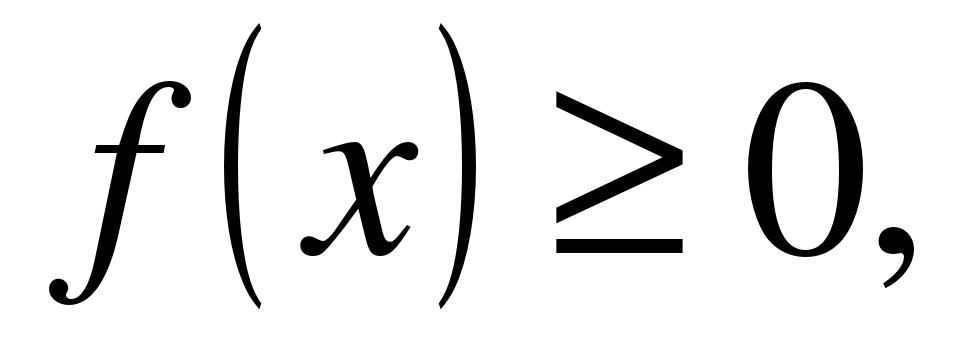 если на рисунке изображен график функции если на рисунке изображен график функции 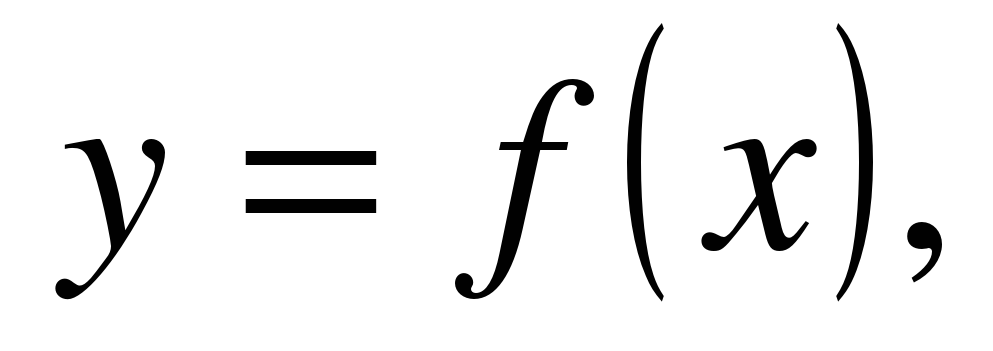 заданной на промежутке заданной на промежутке 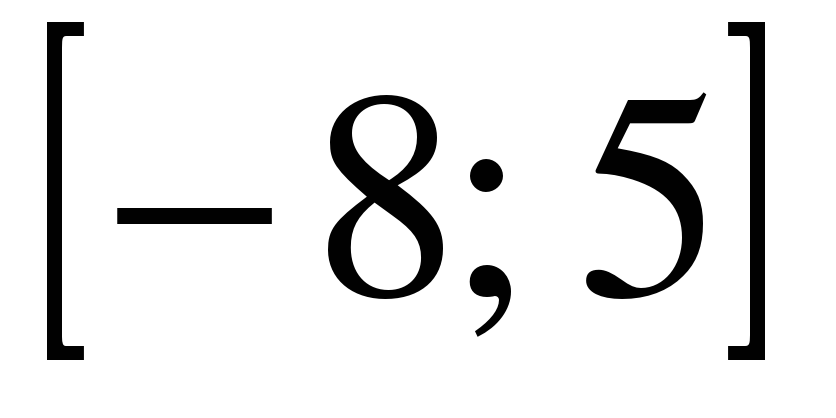 1) 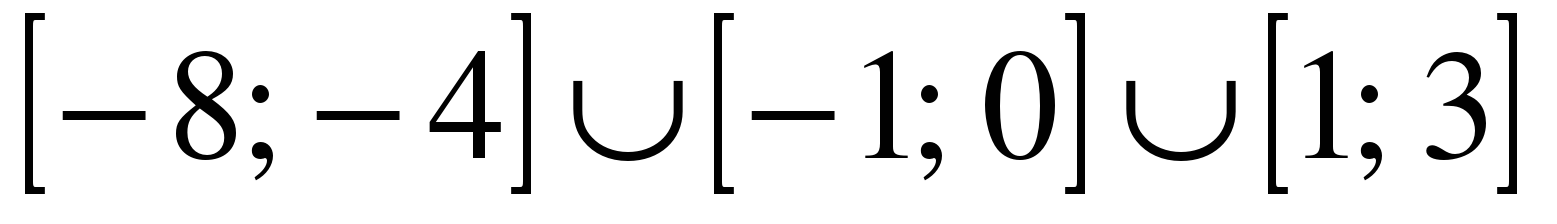 �� �� 2) 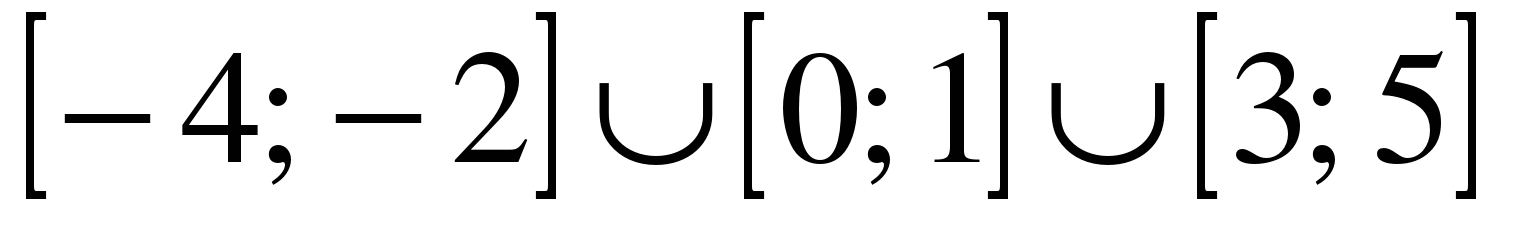 �� �� 3) 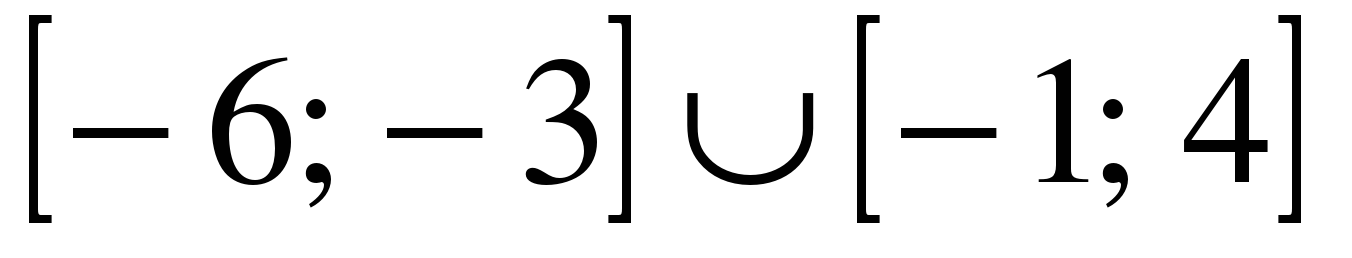 4) 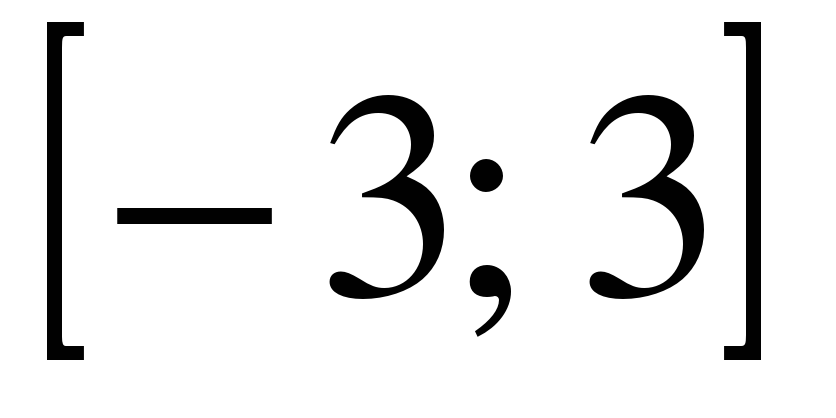 �� ��
| 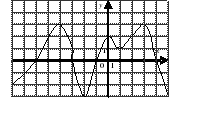 |
|
|
|
|
| A8
| Решите уравнение ��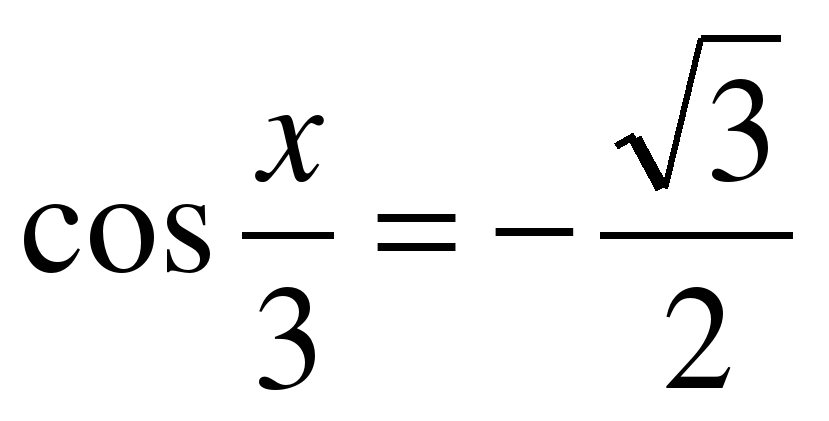 1) 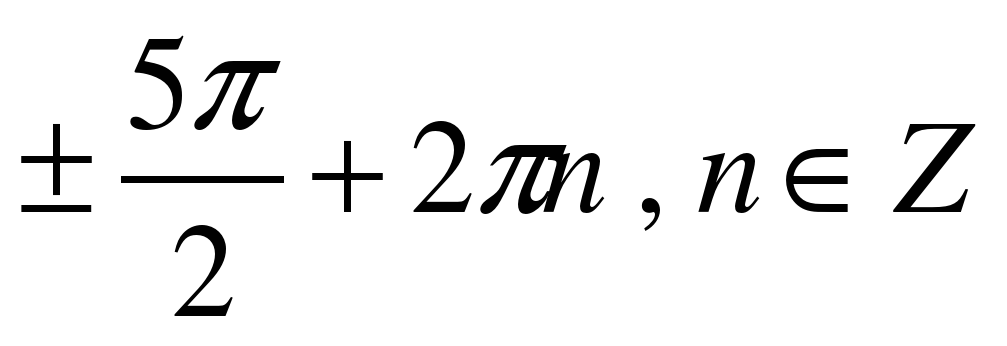 �� �� 2) 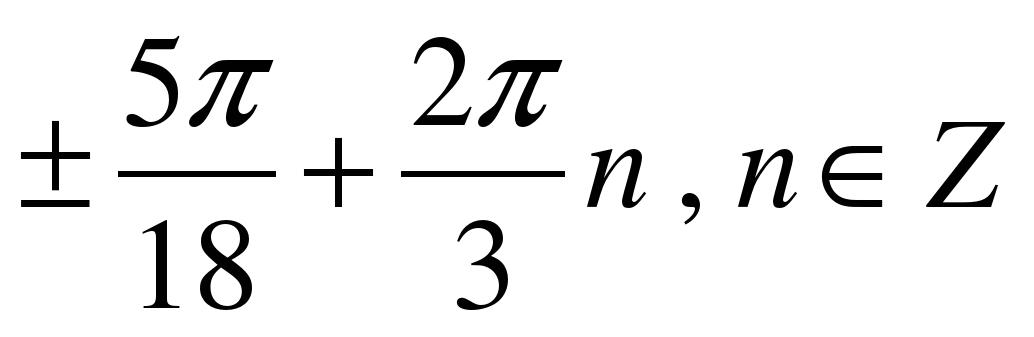 �� �� 3) ��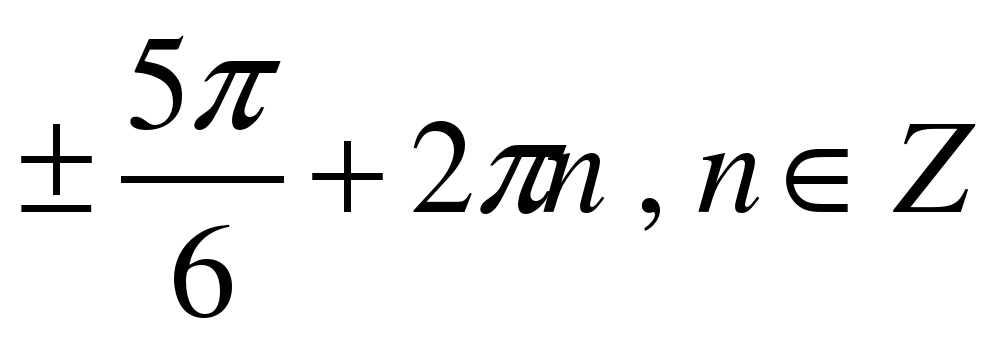 4) 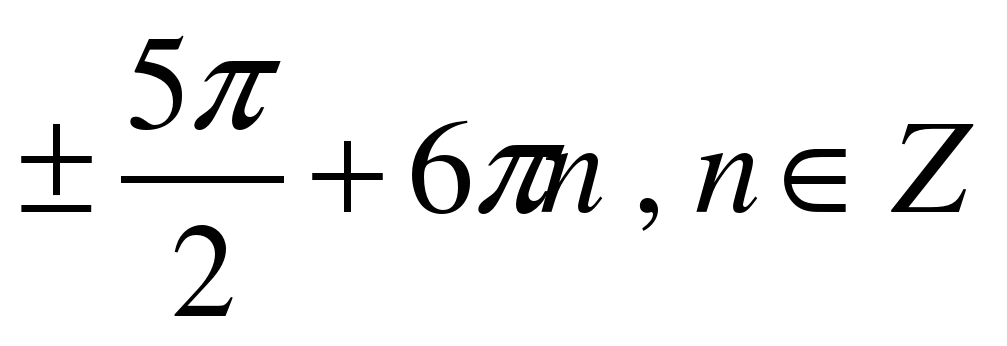 �� ��
|
| A9
| Найдите область определения функции �� 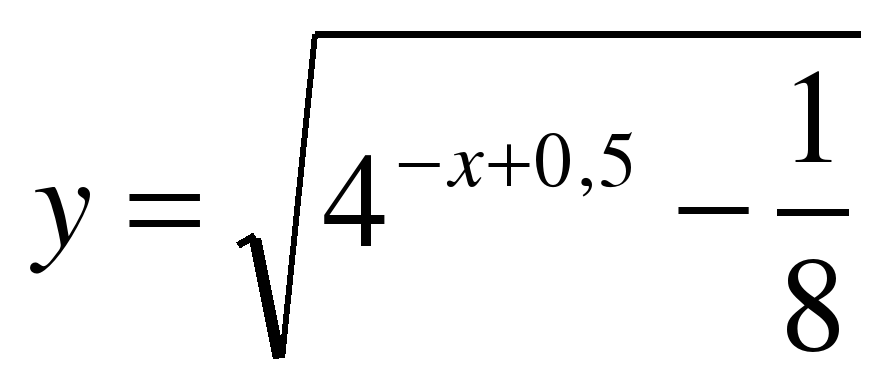 1) 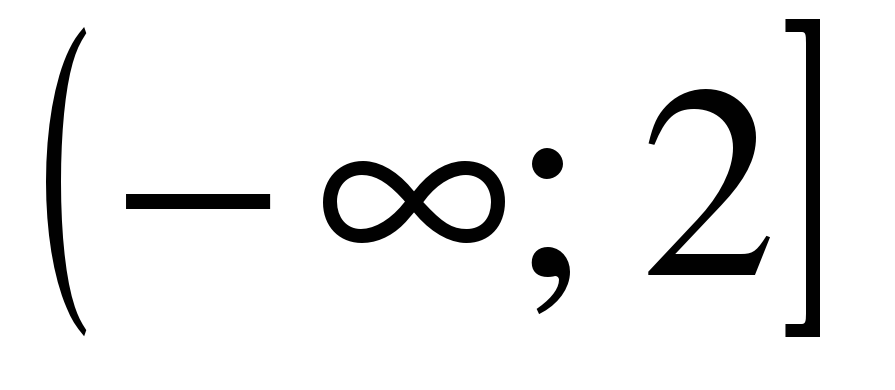 �� 2) �� �� 2) ��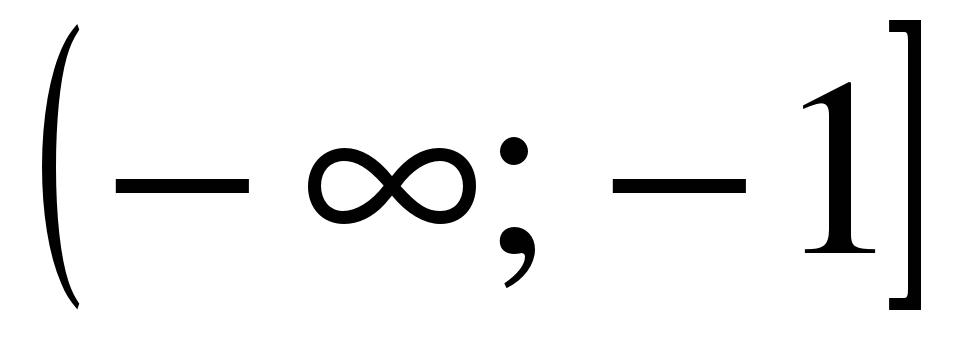 3) 3) 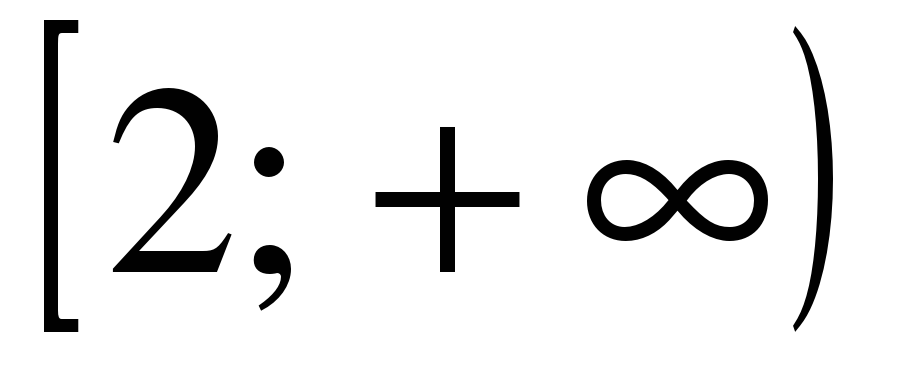 �� 4) �� �� 4) ��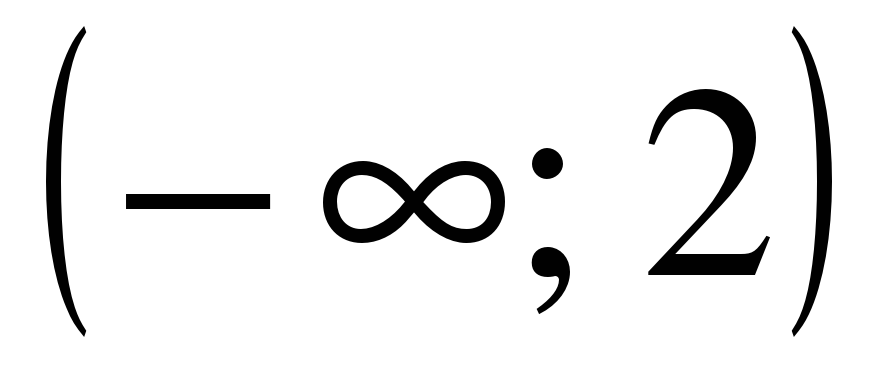
|
|
|
|
|
| Решите неравенство ��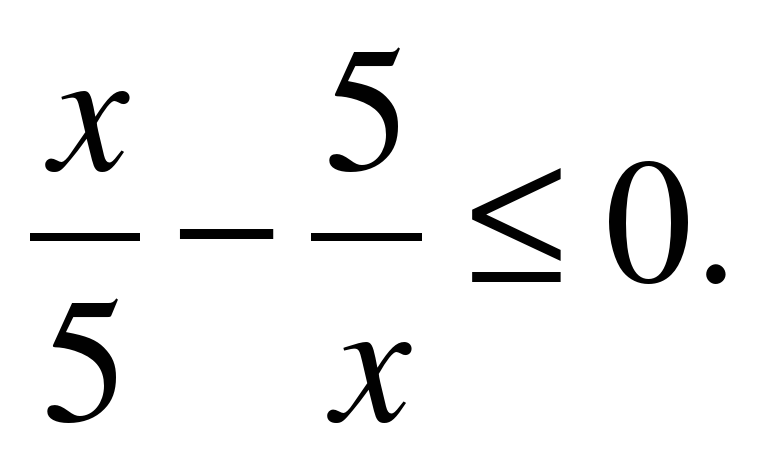 1) 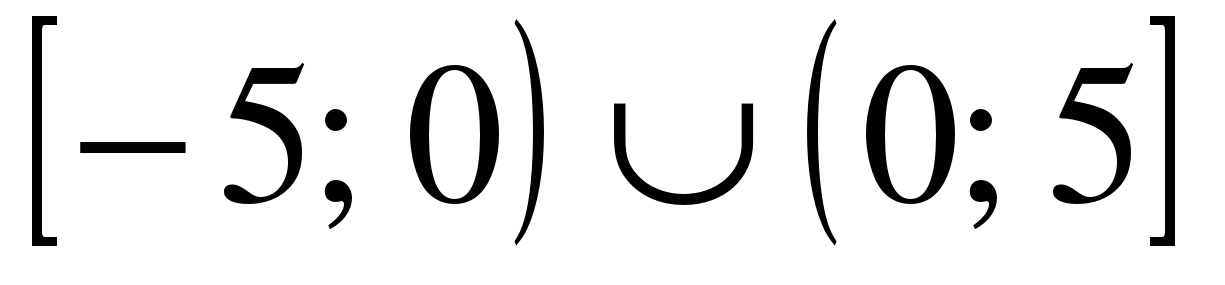 2) 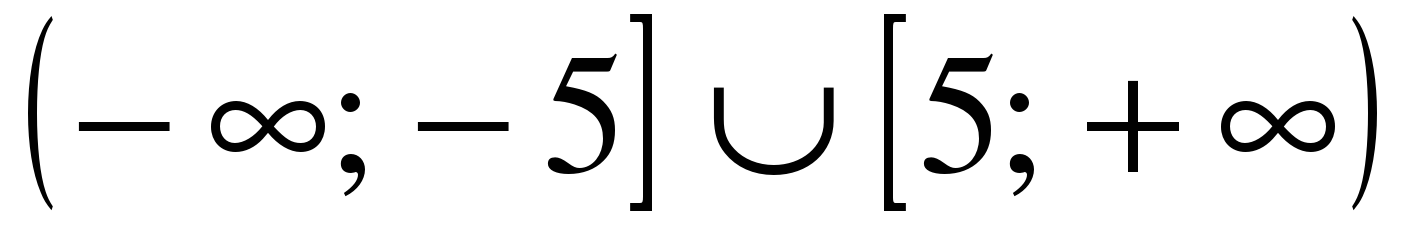 3) 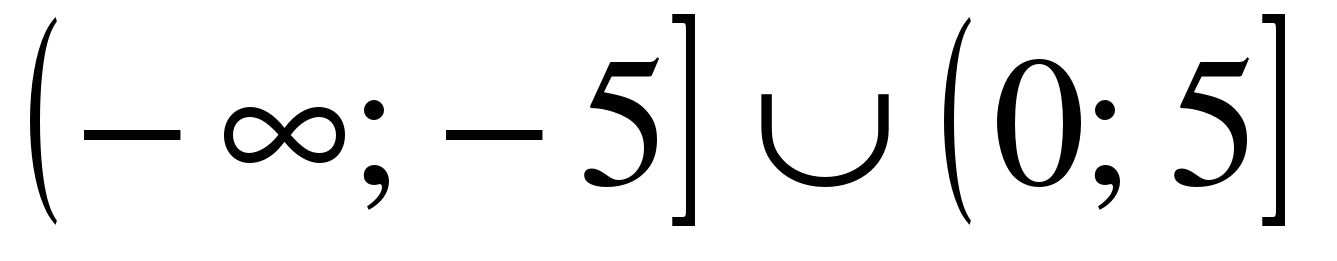 4) ��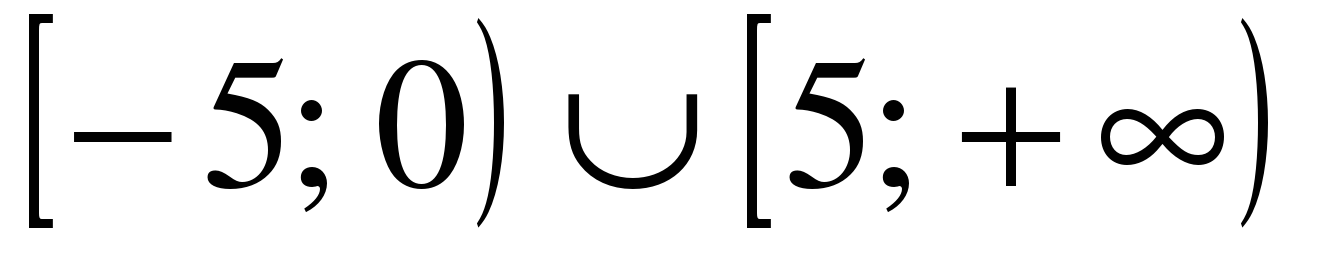
|
A10
| Ответом на задания В1 – В11 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать
в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа
и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно. |
|
| Найдите значение выражения 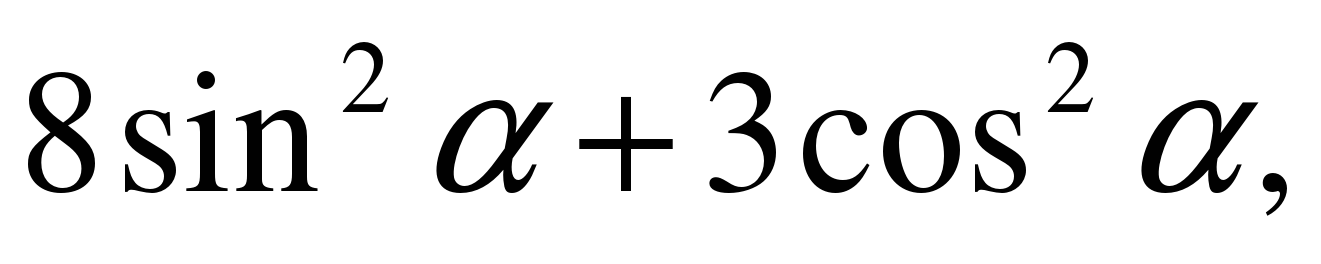 если если 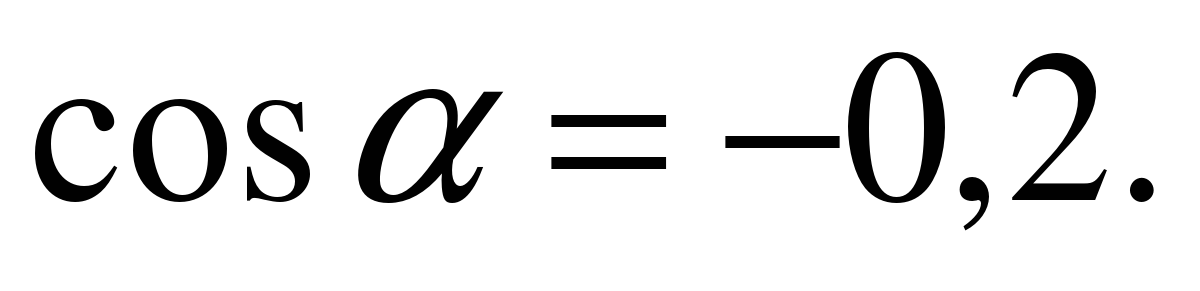
|
|
|
|
|
| Решите уравнение 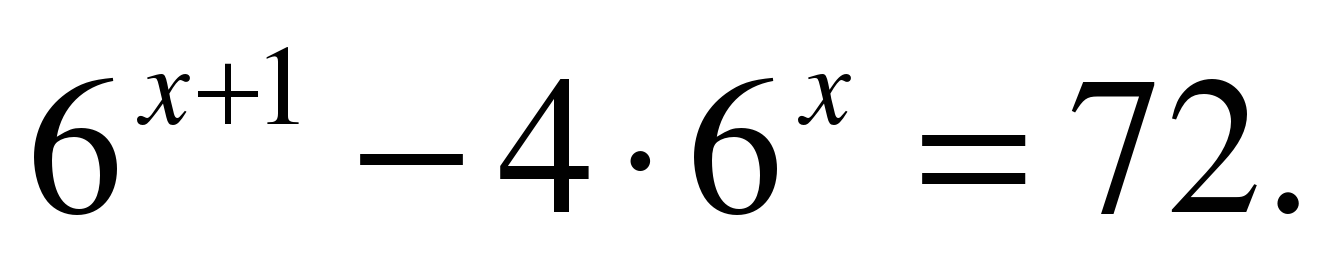 |
|
|
|
|
| Решите уравнение 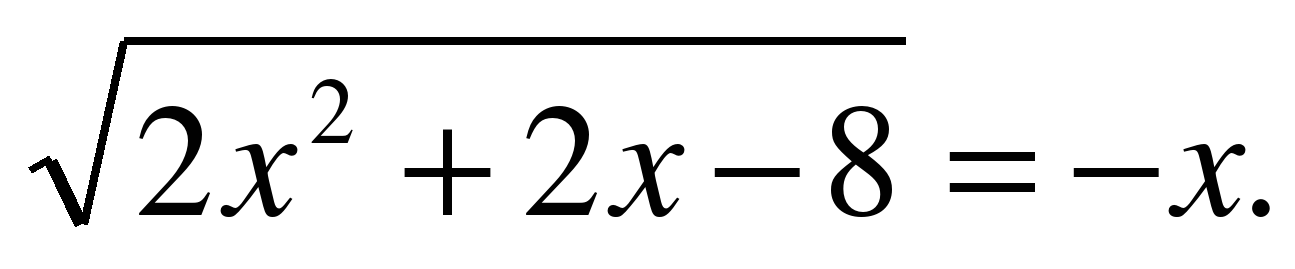 |
|
|
|
|
|
|
B1
B3
B5
B2
ЧАСТЬ 2
B4
|
| Вычислите значение выражения 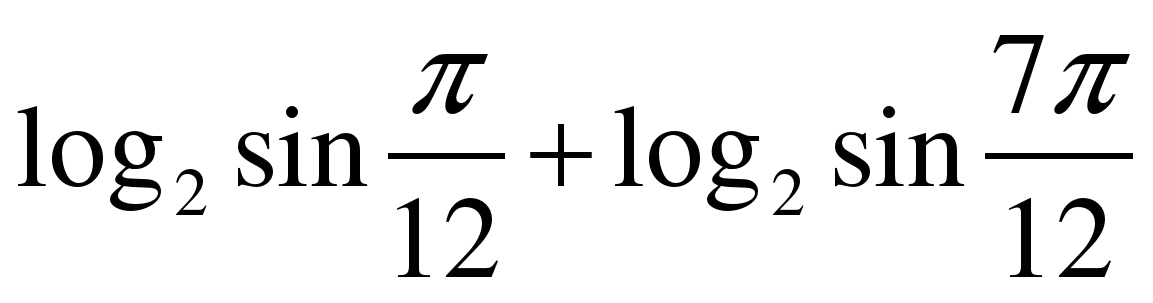 |
|
|
|
|
| Прямая, проходящая через начало координат, касается графика функции 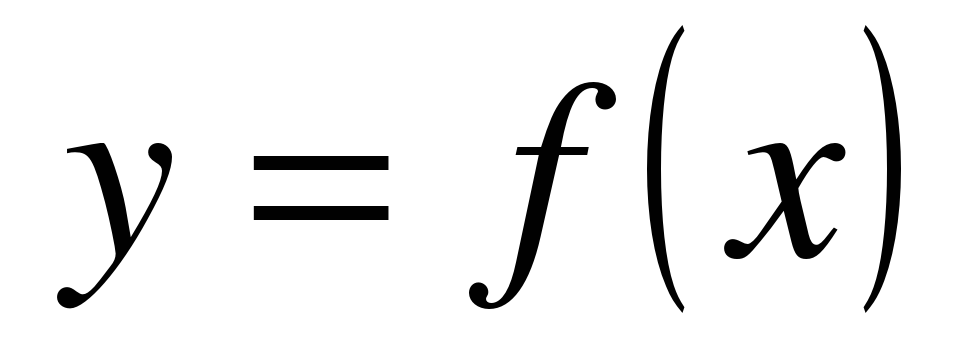 в точке в точке 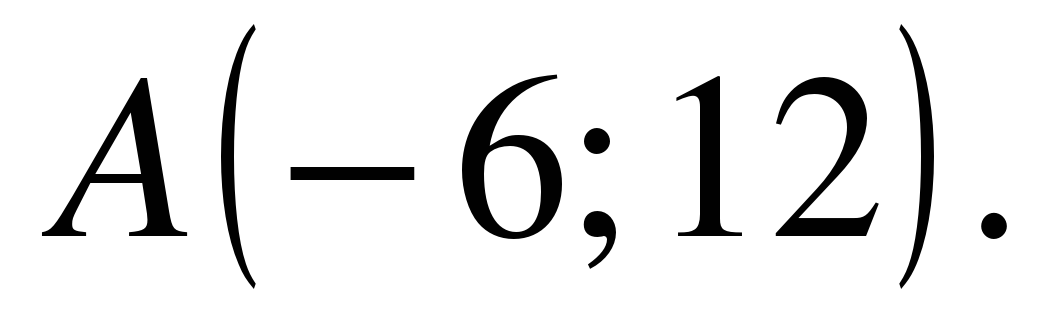 Найдите Найдите 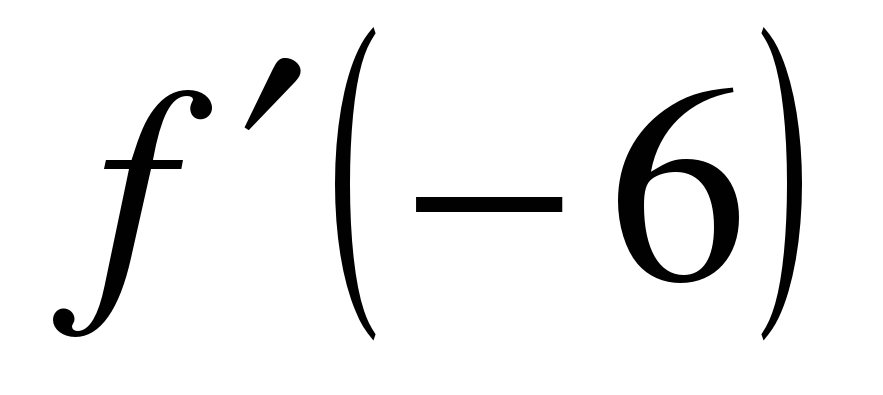 . . |
|
|
|
|
| Найдите количество целочисленных решений неравенства удовлетворяющих неравенству
|
|
|
|
|
| Решите уравнение
|
|
|
|
|
| Функция 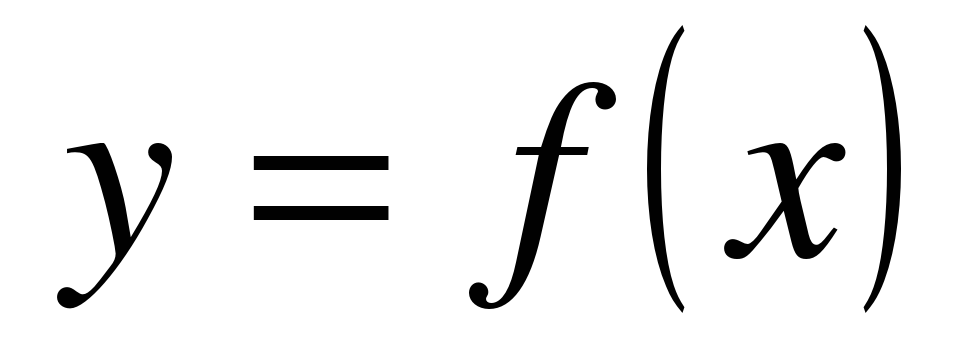 определена на всей числовой прямой и является периодической с периодом 4. Известно, что и Найдите значение выражения определена на всей числовой прямой и является периодической с периодом 4. Известно, что и Найдите значение выражения
|
|
|
|
*B9
|
| В бидон налили 4 литра молока трехпроцентной жирности и 6 литров молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?
|
|
|
|
*B10
Боковое ребро прямой призмы ABCA1B1C1 равно 16. Основание призмы – треугольник АВС, площадь которого равна 4, ВС = 3. Найдите тангенс угла между плоскостями А1ВС и АВС.
B6
B7
B8
*B11
В параллелограмме ABCD биссектриса угла В пересекает сторону CD в точке Т и прямую AD в точке М. Найдите периметр треугольника СВТ, если АВ = 21, ВМ = 35, MD = 9.
| Для записи ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем решение. |
|
|
| Найдите точки максимума функции
|
|
|
|
|
| Найдите абсциссы всех точек пересечения графиков функций и
|
|
| ЧАСТЬ 3
|
|
| | Для записи ответов на задания (С3 – С5) используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем обоснованное решение. |
|
|
|
|
C3
|
| Найдите все значения а, для каждого из которых найдется х из промежутка [0; 2) такое, что значение выражения равно значению выражения
|
|
|
|
*C4
|
| Дана сфера диаметром 26. Сечением сферы плоскостью, удаленной от центра сферы на расстояние 5, является окружность с диаметром АВ. Точка D выбрана на сфере, а точка С – на окружности сечения так, что объем пирамиды DABC наибольший. Найдите площадь треугольника DMN, где M и N – середины ребер АС и ВС соответственно.
|
|
|
|
|
| Решите уравнение , если известно, что и |
C2
C5
C1
8
Просмотр содержимого документа
«Математика_11вариант»
Просмотр содержимого документа
«Математика_12вариант»
Просмотр содержимого документа
«Математика_13вариант»
Просмотр содержимого документа
«Математика_14вариант»
ЕГЭ по МАТЕМАТИКЕ
Вариант № 14
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается
4 часа (240 мин). Работа состоит из трех частей и содержит 26 заданий.
Часть 1 содержит 13 заданий (А1 – А10 и В1 – В3) обязательного уровня по материалу курса «Алгебра и начала анализа» 10-11 классов.
К каждому заданию А1 – А10 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ.
Часть 2 содержит 10 более сложных заданий (В4 – В11, С1, С2) по материалу курса «Алгебра и начала анализа» 10-11 классов, а также различных разделов курсов алгебры и геометрии основной и средней школы. К заданиям В4 – В11 надо дать краткий ответ, к заданиям С1 и С2 – записать решение.
Часть 3 содержит 3 самых сложных задания, два – алгебраических
(С3, С5) и одно – геометрическое (С4). При их выполнении надо записать обоснованное решение.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха!
ЧАСТЬ 1
| При выполнении заданий А1 – А10 в бланке ответов № 1 под номером выполняемого задания поставьте знак "´" в клеточке, номер которой соответствует номеру выбранного вами ответа. |
| A1
| Найдите значение выражения ��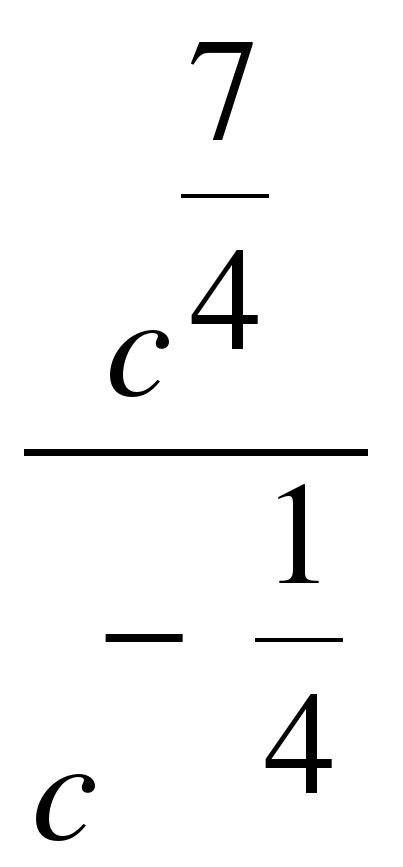 при с = 3 при с = 3 1) 9 2) ��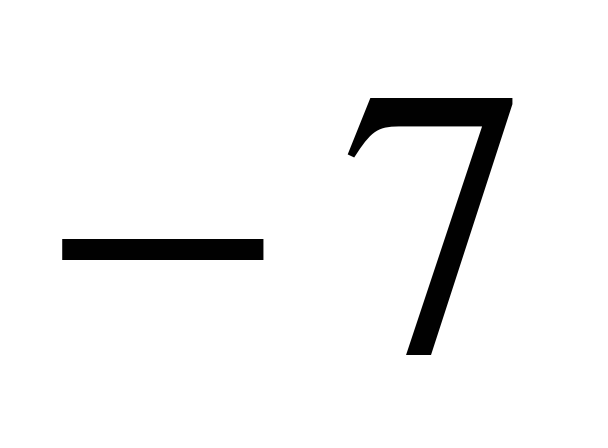 3) �� 3) ��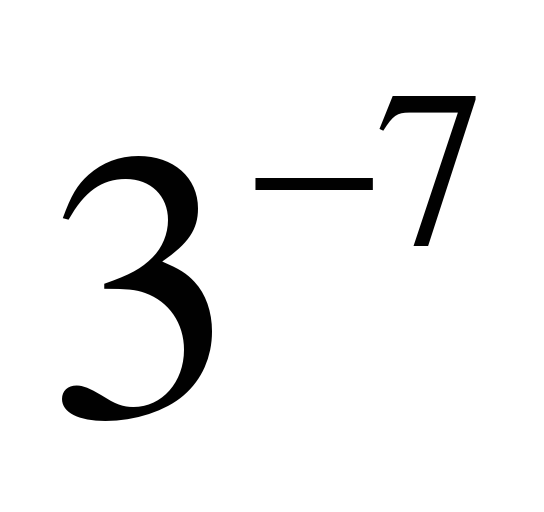 4)�� 4)�� 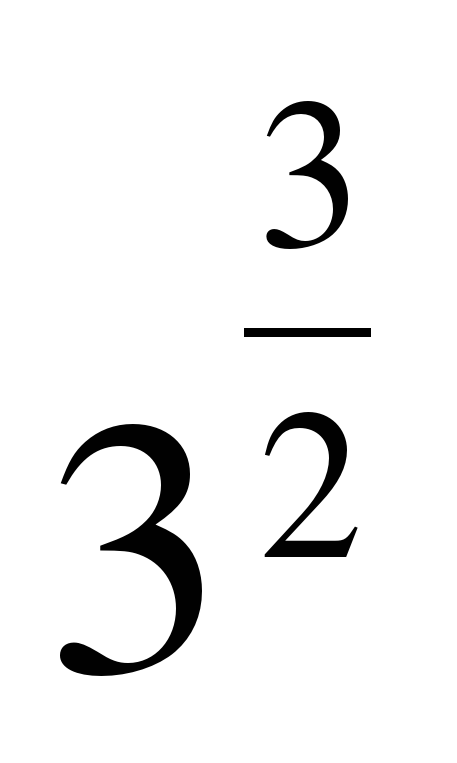 . .
|
|
|
|
| A2
| Вычислите: ��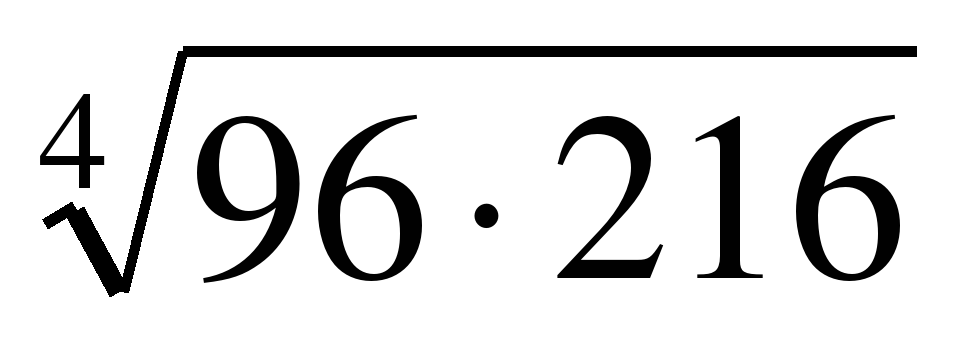 1) 144 2) 12 3) 72 4) 24
|
|
|
|
| A3
| Вычислите: �� 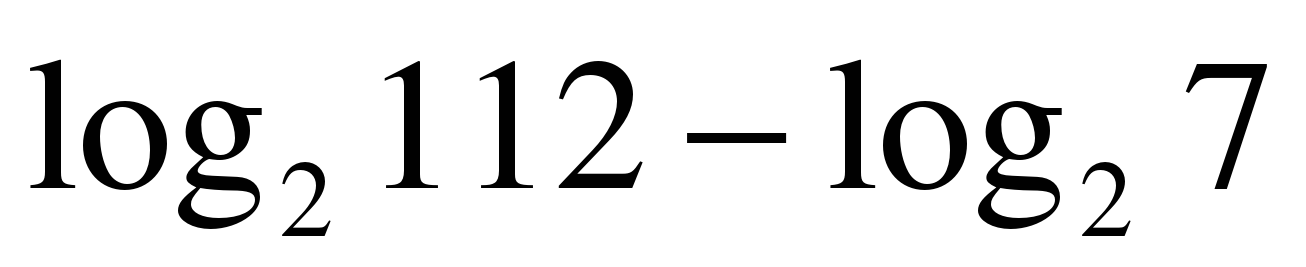 1) 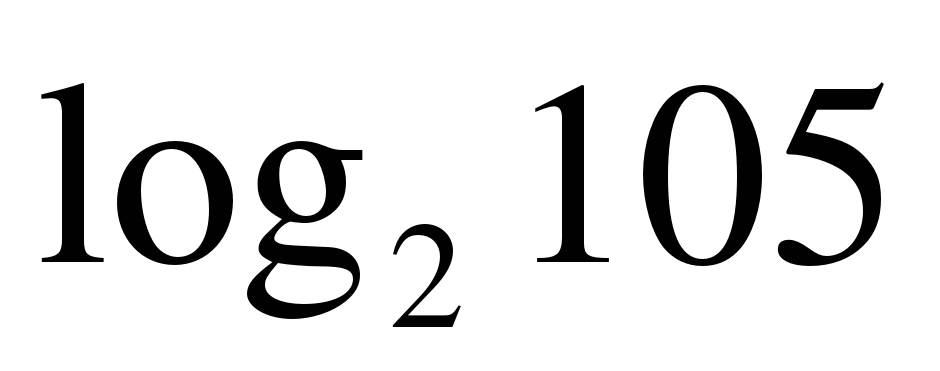 2) 16 3) 8 4) 4�� 2) 16 3) 8 4) 4�� |
|
|
|
| A4
| На каком из следующих рисунков функция, заданная графиком, возрастает на промежутке [0;2] ?
|
| A5
| Найдите производную функции �� 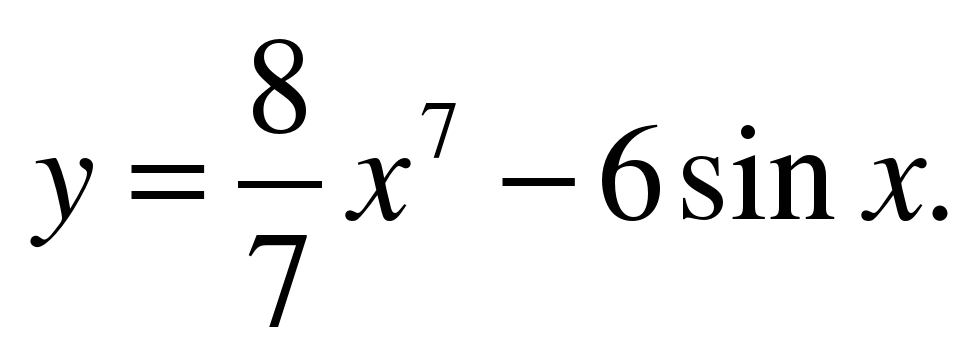 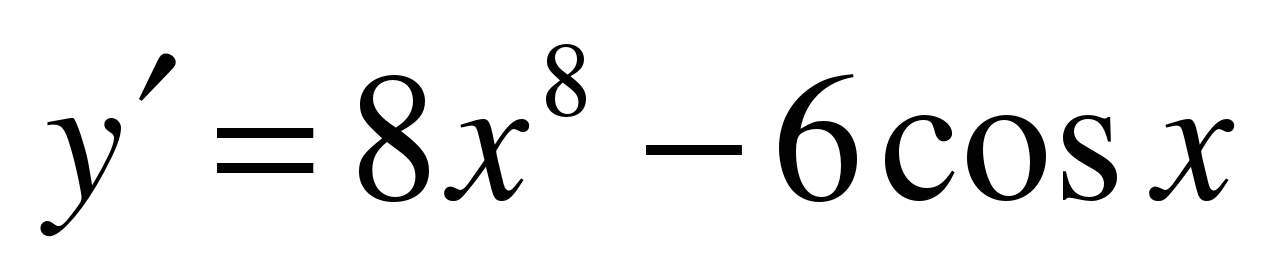 �� 3) �� �� 3) ��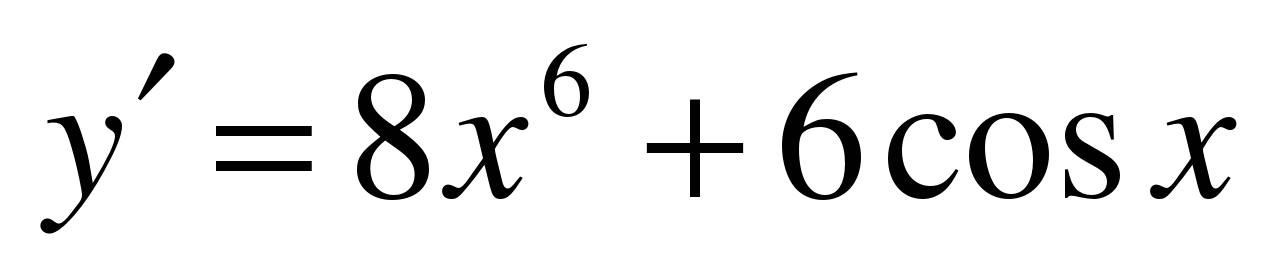  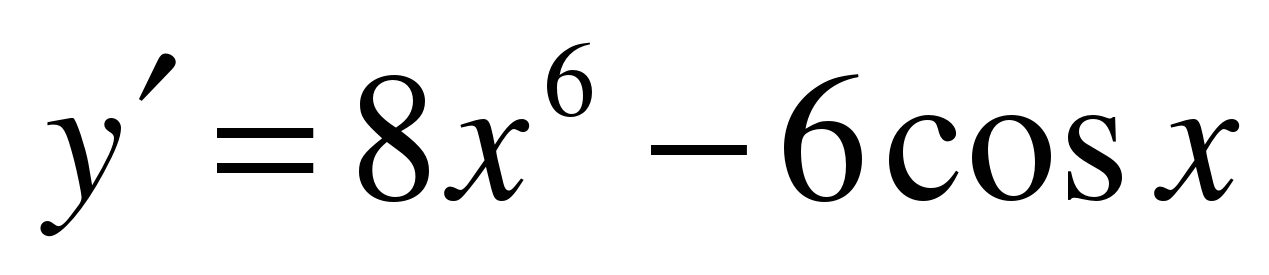 �� 4) �� �� 4) ��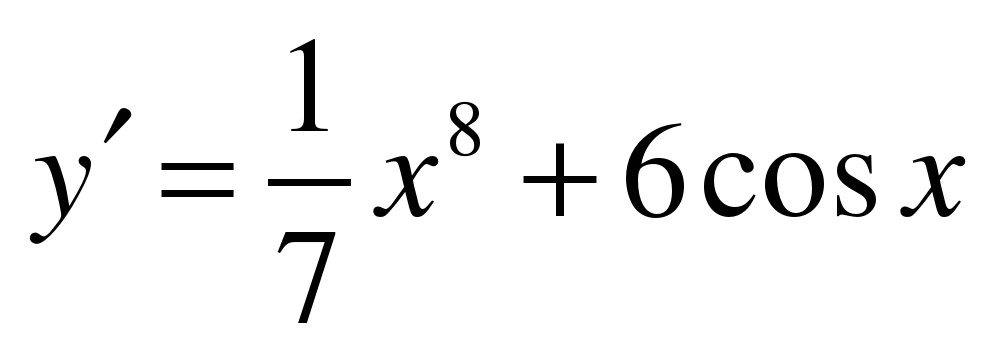
|
|
|
|
| A6
| Найдите множество значений функции �� 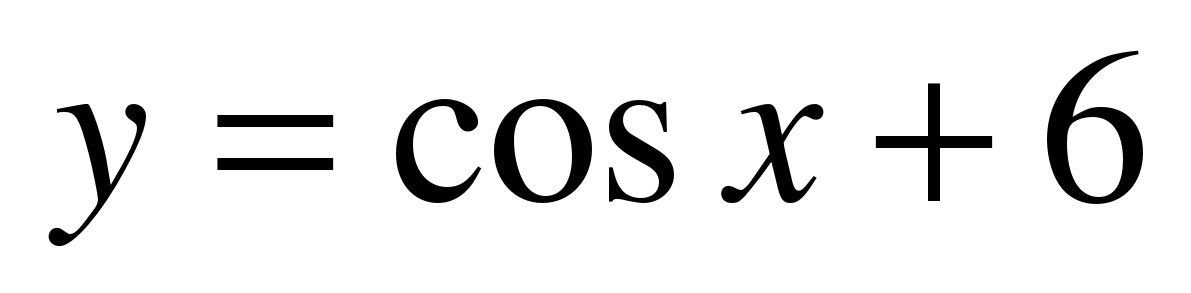 . . 1) 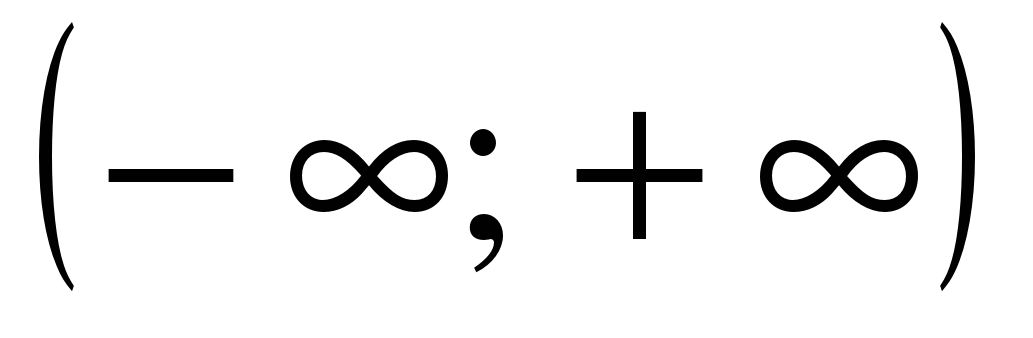 2) [–1; 1] 3) [5; 7]�� 4) [6; 7]. 2) [–1; 1] 3) [5; 7]�� 4) [6; 7].
|
|
|
|
| A7
| | Решите неравенство 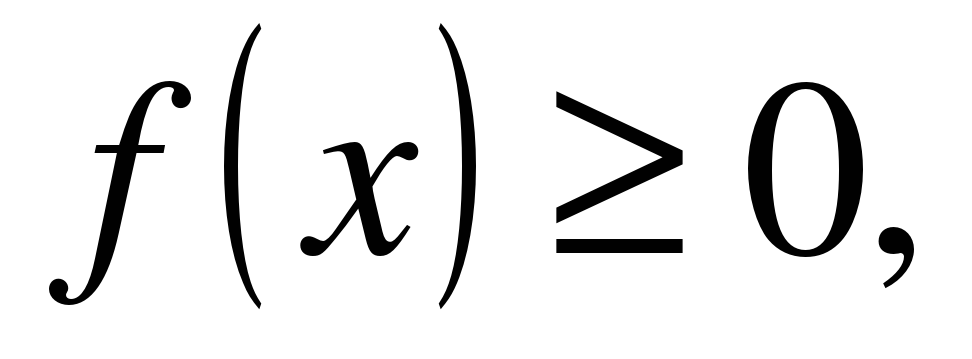 если на рисунке изображен график функции если на рисунке изображен график функции 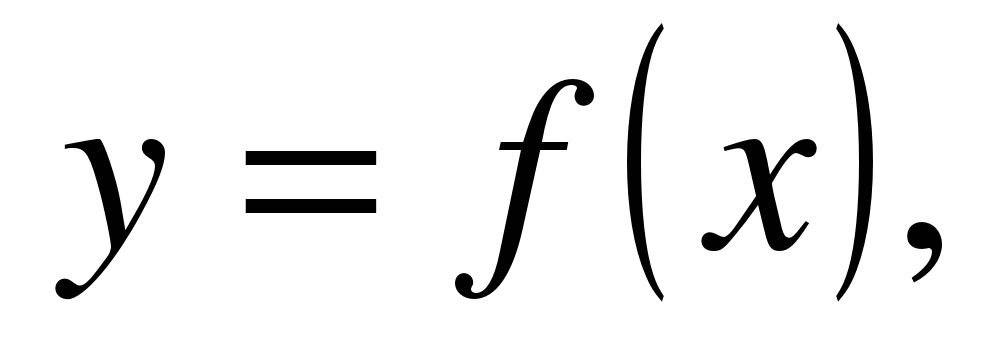 заданной на промежутке заданной на промежутке 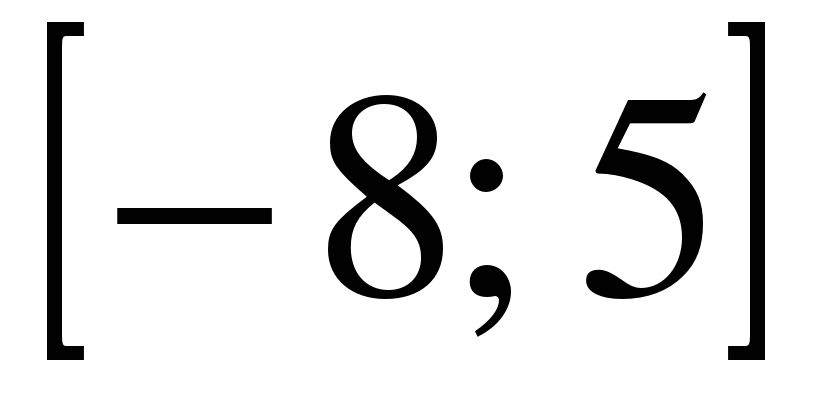 1) 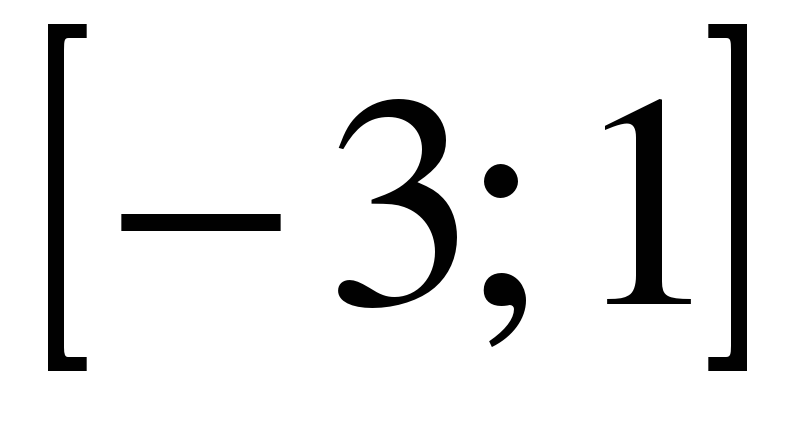 �� �� 2) 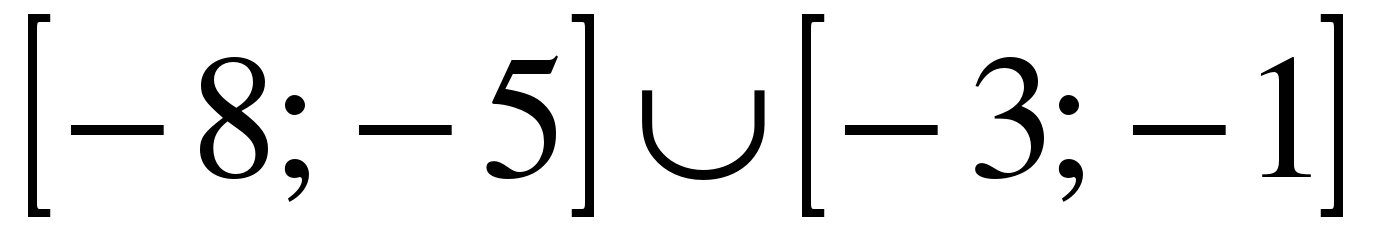 �� �� 3)  4) 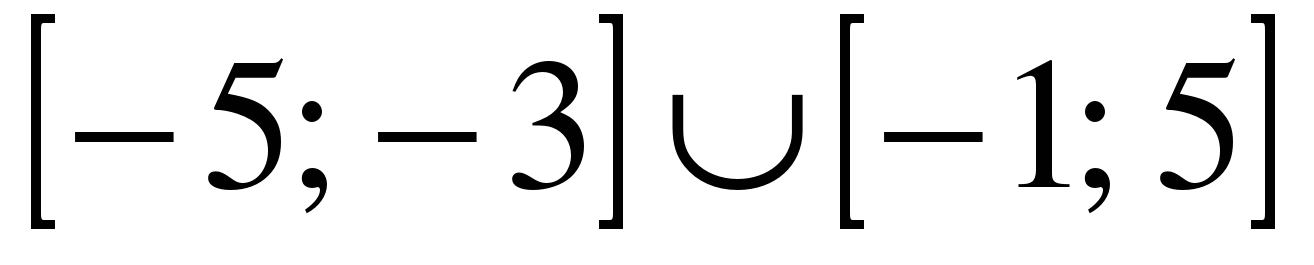 �� ��
| 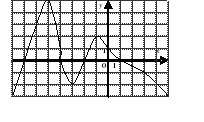 |
|
|
|
|
| A8
| Решите уравнение ��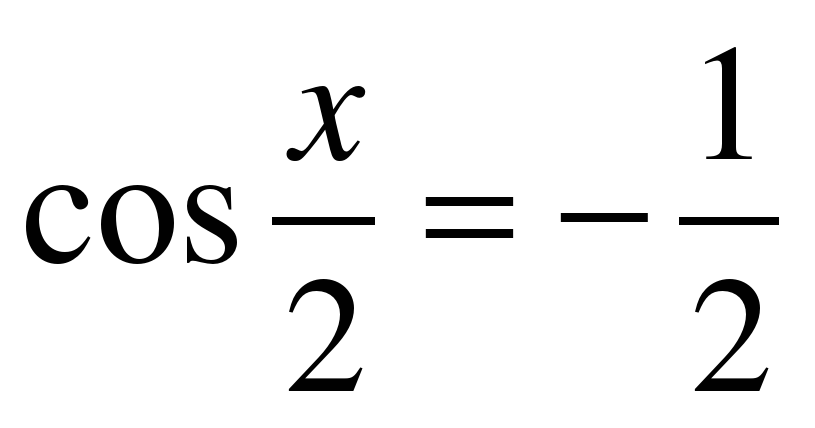 . . 1) 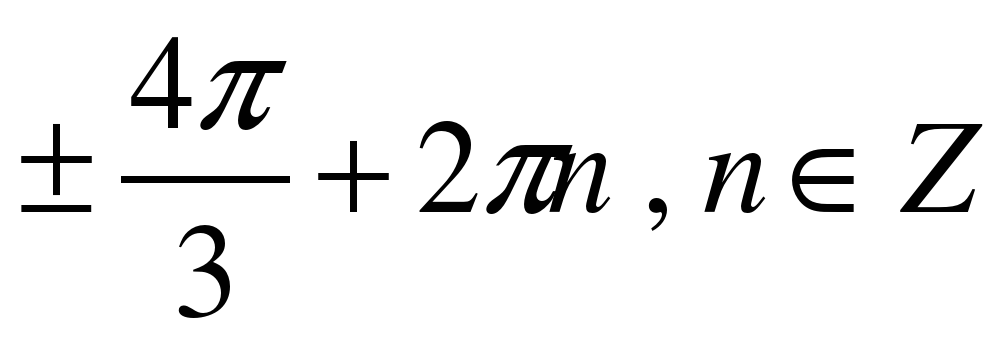 �� �� 2) 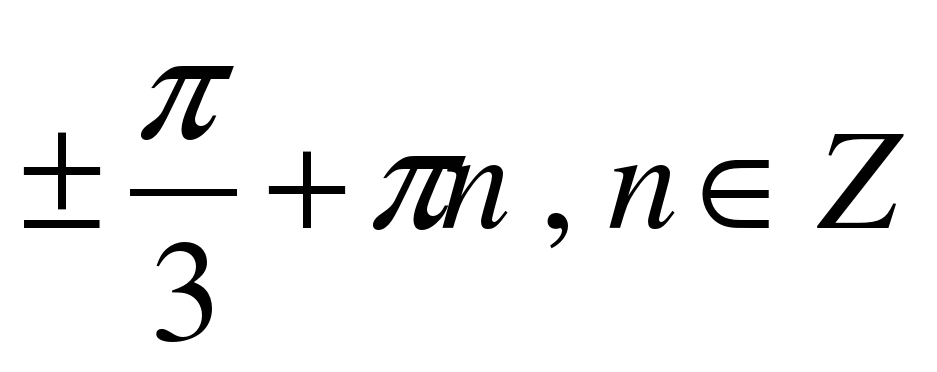 �� �� 3) ��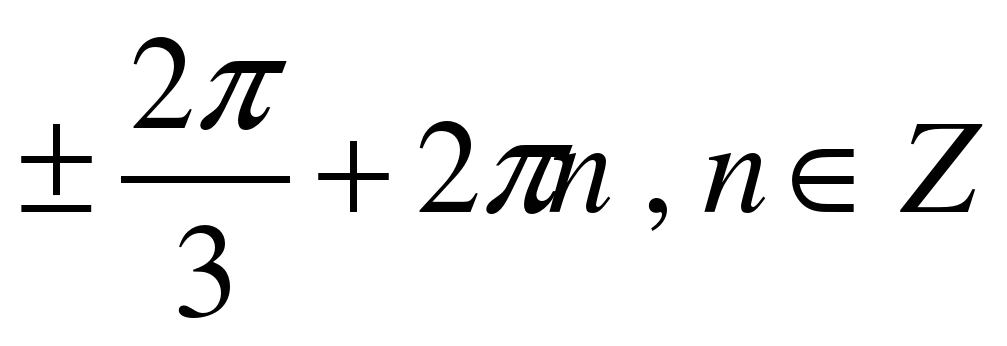 4) 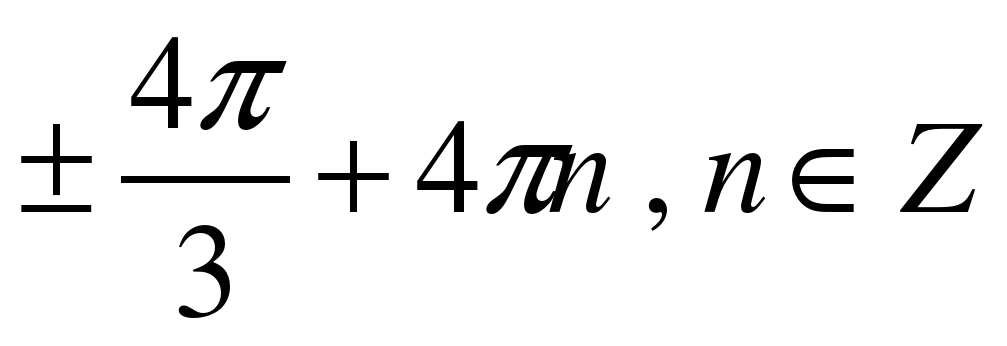
�� |
| A9
| Найдите область определения функции �� 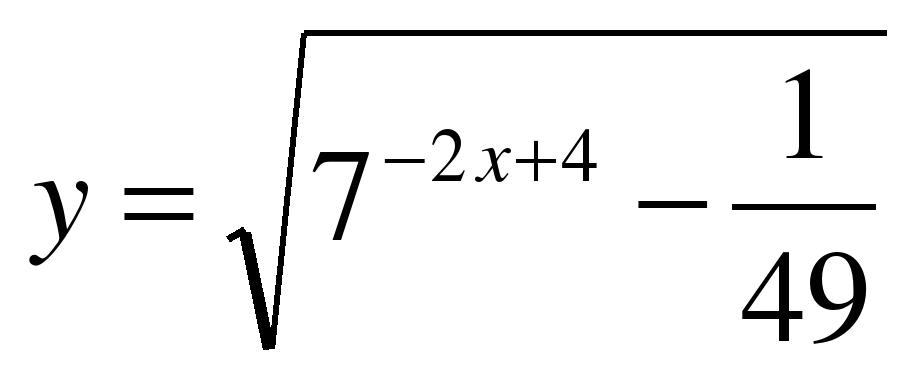 1) 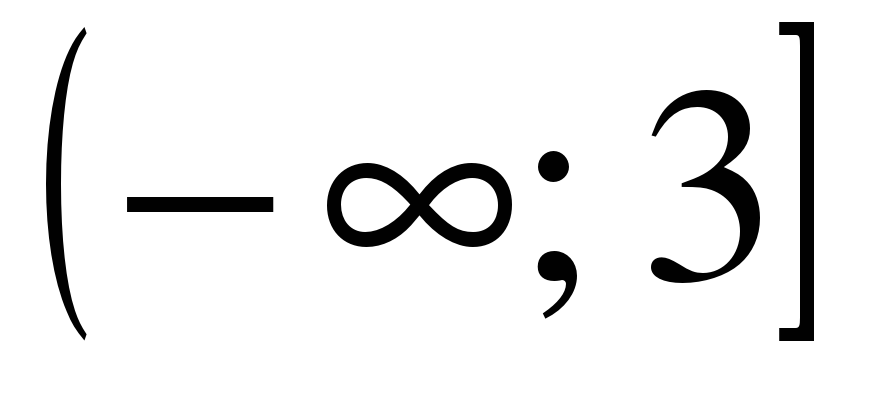 �� 2) �� �� 2) ��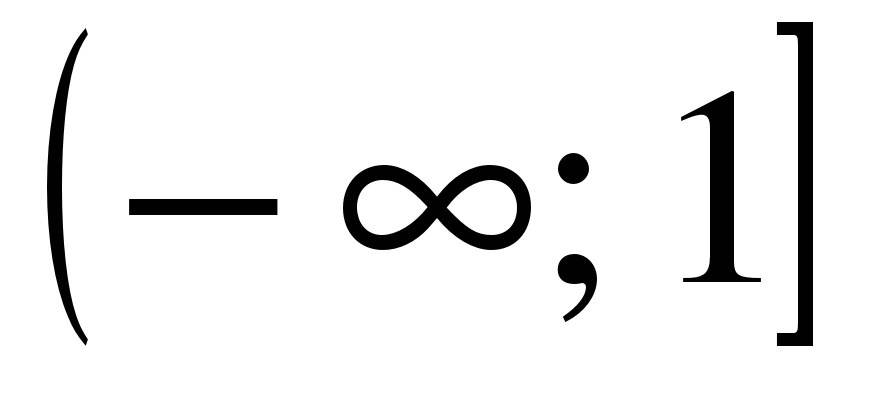 3) 3) 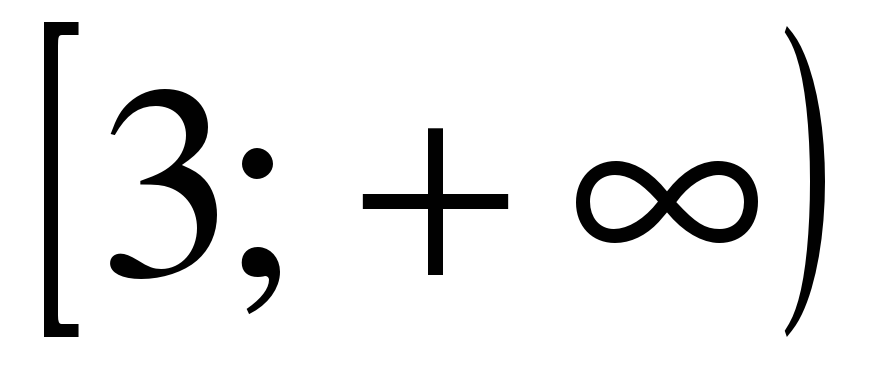 �� 4) �� �� 4) ��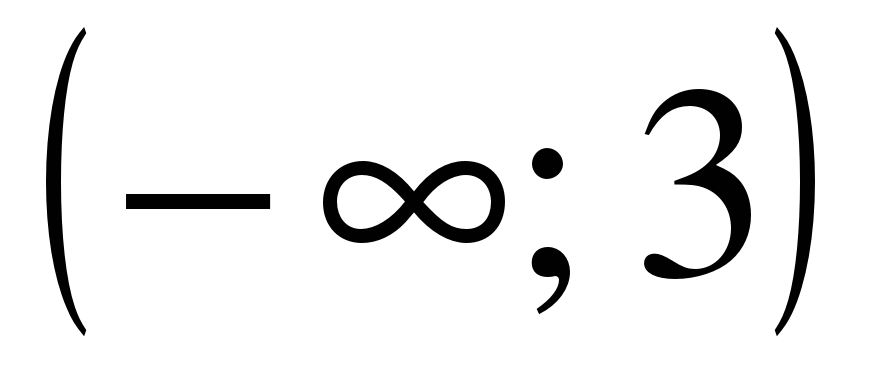
|
|
|
|
|
| Решите неравенство ��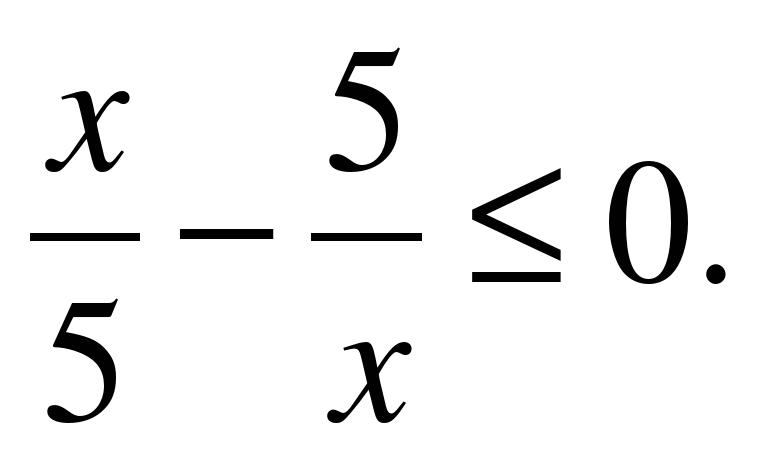 1) 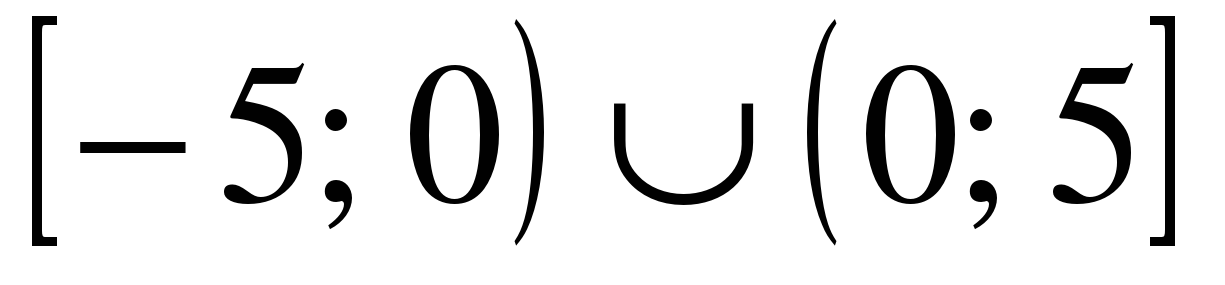 2) 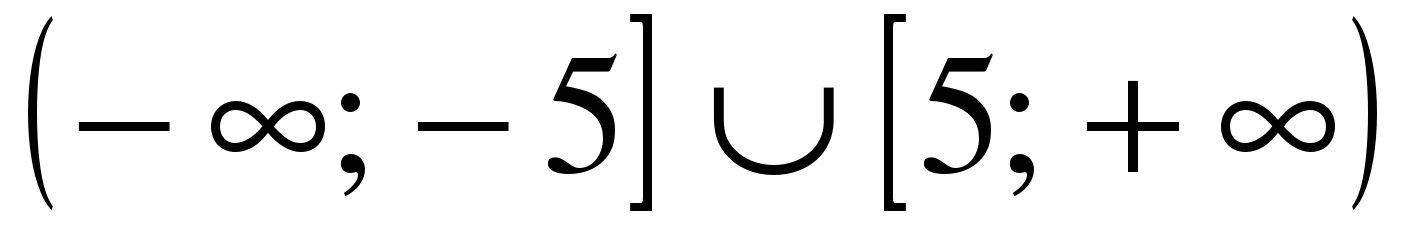 3) 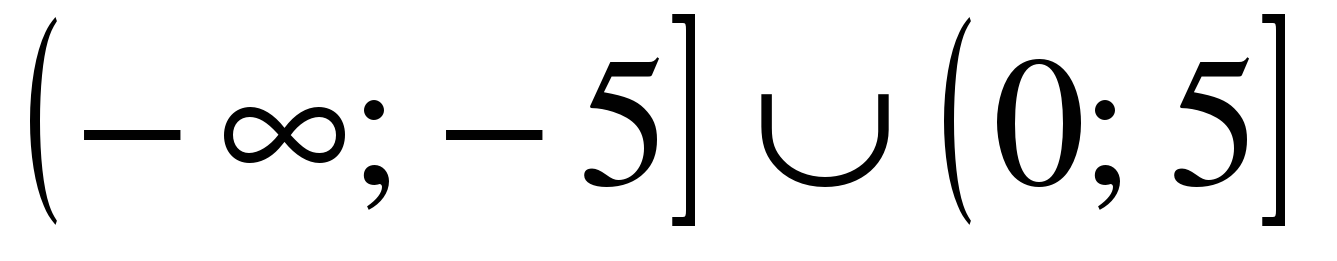 4) ��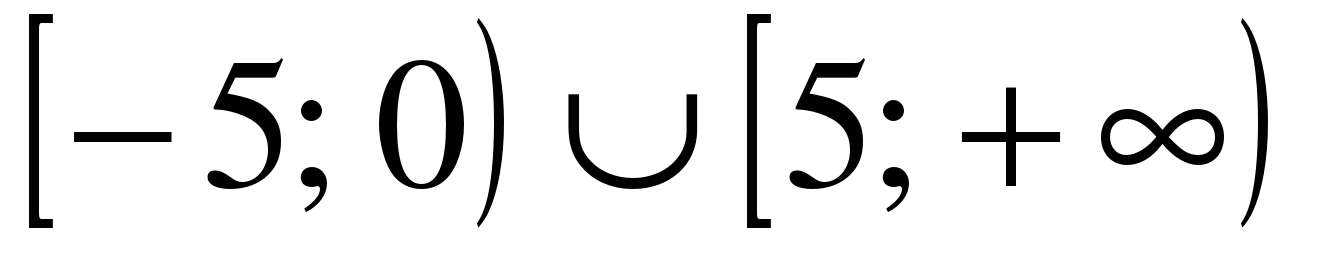
|
A10
| Ответом на задания В1 – В11 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать
в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа
и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно. |
|
| Найдите значение выражения 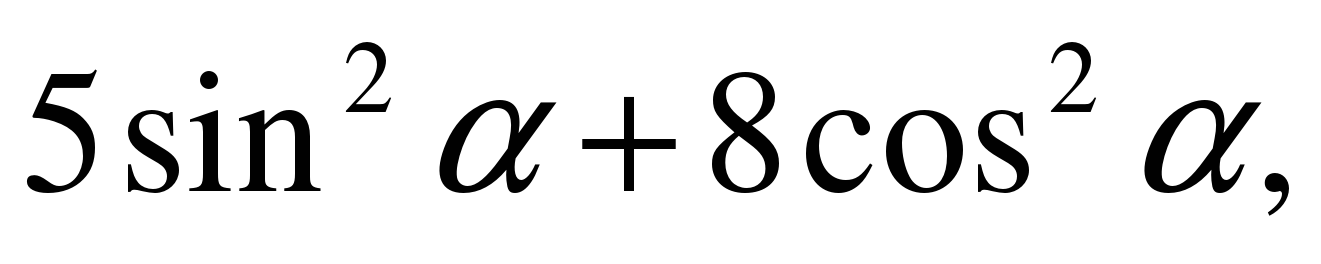 если если 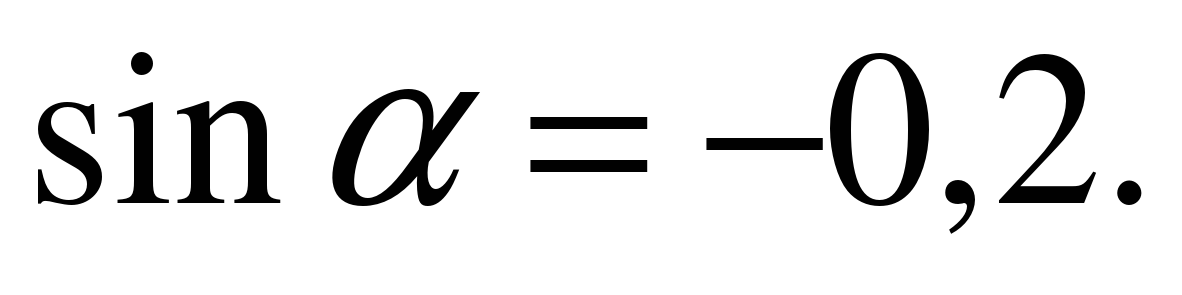
|
|
|
|
|
| Решите уравнение 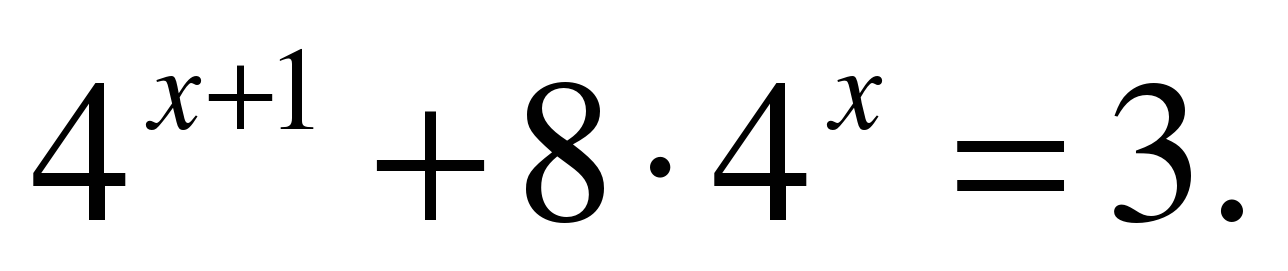
|
|
|
|
|
| Решите уравнение 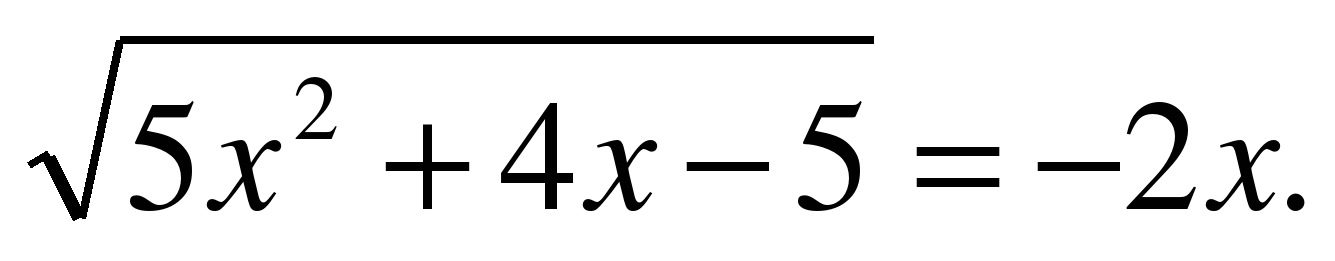 |
|
|
|
|
|
|
B1
B3
B2
ЧАСТЬ 2
B4
|
| Вычислите значение выражения 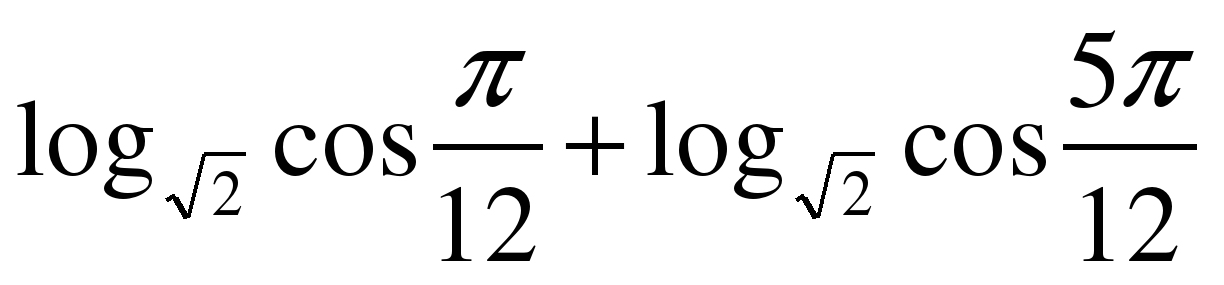 |
|
|
|
| В5 | Прямая, проходящая через начало координат, касается графика функции 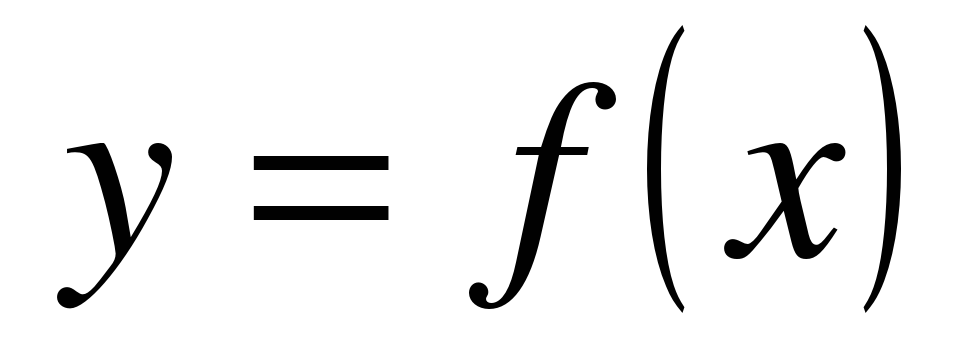 в точке в точке 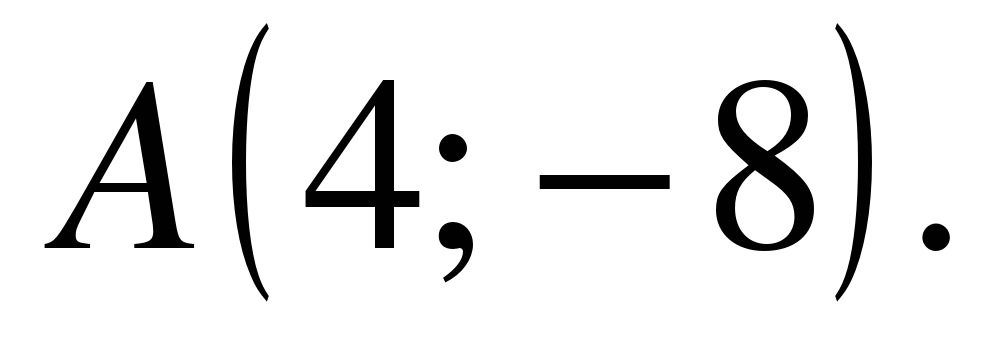 Найдите Найдите 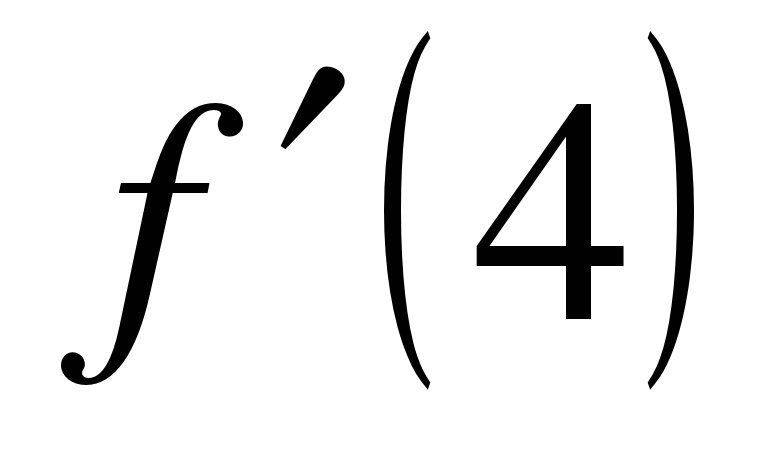 . .
|
|
|
|
|
|
|
| Найдите количество целочисленных решений неравенства удовлетворяющих неравенству
|
|
|
|
|
| Решите уравнение
|
|
|
|
|
| Функция 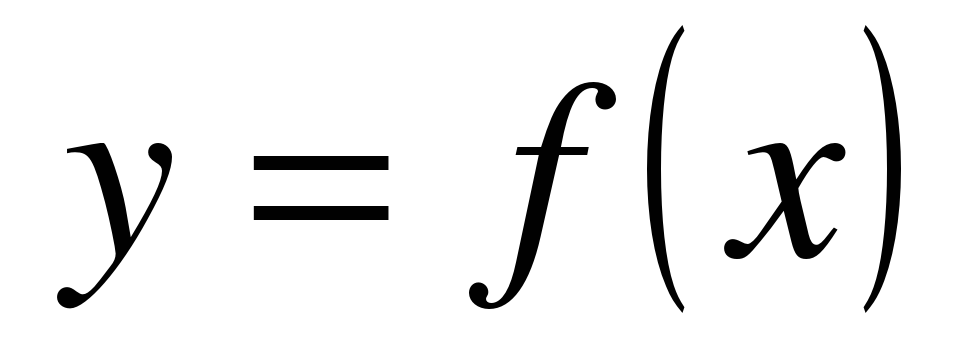 определена на всей числовой прямой и является периодической с периодом 4. Известно, что и Найдите значение выражения определена на всей числовой прямой и является периодической с периодом 4. Известно, что и Найдите значение выражения
|
*B9
|
|
|
|
| За январь, февраль, март зарплата составила в сумме 15900 рублей, а за апрель, май, июнь – 18600 рублей, при этом в течение календарного года она ежемесячно увеличивалась на одну и ту же величину. Определите зарплату за сентябрь.
|
*B10
Основание прямой призмы ABCDA1B1C1D1 – ромб ABCD с углом 150 и стороной, равной 2. Тангенс угла между плоскостью основания призмы и плоскостью ABC1 равен 4,2. Найдите высоту призмы.
B6
B7
B8
*B11
Найдите радиус окружности, вписанной в равнобедренную трапецию, если средняя линия трапеции равна , а косинус угла при основании трапеции равен
| Для записи ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем решение. |
|
|
| Найдите наименьшее значение функции
|
|
|
|
|
| Решите уравнение
|
|
| ЧАСТЬ 3
|
|
| | Для записи ответов на задания (С3 – С5) используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем обоснованное решение. |
|
|
|
|
|
| Найдите все значения а, для каждого из которых найдется х из промежутка [4; 9) такое, что значение выражения равно значению выражения
|
|
|
|
*C4
|
| Дана сфера диаметром 26. Сечением сферы плоскостью, удаленной от центра сферы на расстояние 5, является окружность с диаметром АВ. Точка D выбрана на сфере, а точка С – на окружности сечения так, что объем пирамиды DABC наибольший. Найдите площадь треугольника DMN, где M и N – середины ребер АС и ВС соответственно.
|
|
|
|
|
| Решите уравнение , если известно, что и |
C2
C3
C5
C1
8
Просмотр содержимого документа
«Математика_15вариант»
ЕГЭ по МАТЕМАТИКЕ
Вариант № 15
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается
4 часа (240 мин). Работа состоит из трех частей и содержит 26 заданий.
Часть 1 содержит 13 заданий (А1 – А10 и В1 – В3) обязательного уровня по материалу курса «Алгебра и начала анализа» 10-11 классов.
К каждому заданию А1 – А10 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ.
Часть 2 содержит 10 более сложных заданий (В4 – В11, С1, С2) по материалу курса «Алгебра и начала анализа» 10-11 классов, а также различных разделов курсов алгебры и геометрии основной и средней школы. К заданиям В4 – В11 надо дать краткий от вет, к заданиям С1 и С2 – записать решение.
Часть 3 содержит 3 самых сложных задания, два – алгебраических
(С3, С5) и одно – геометрическое (С4). При их выполнении надо записать обоснованное решение.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха!
ЧАСТЬ 1
| При выполнении заданий А1 – А10 в бланке ответов № 1 под номером выполняемого задания поставьте знак "´" в клеточке, номер которой соответствует номеру выбранного вами ответа. |
| A1
| Найдите значение выражения ��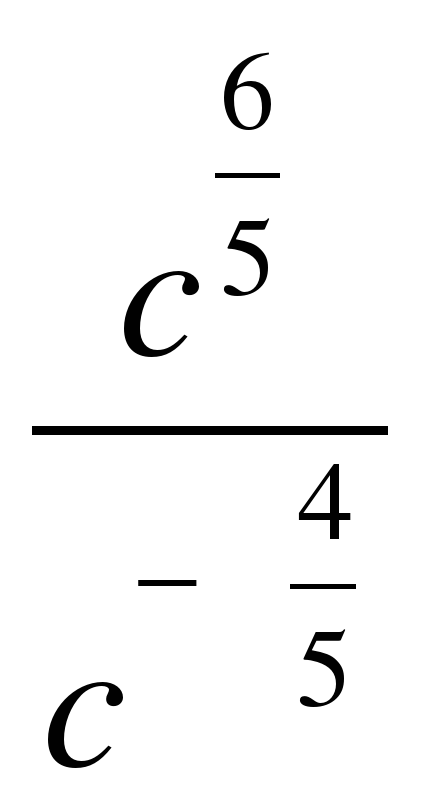 при с = 2 при с = 2 1) 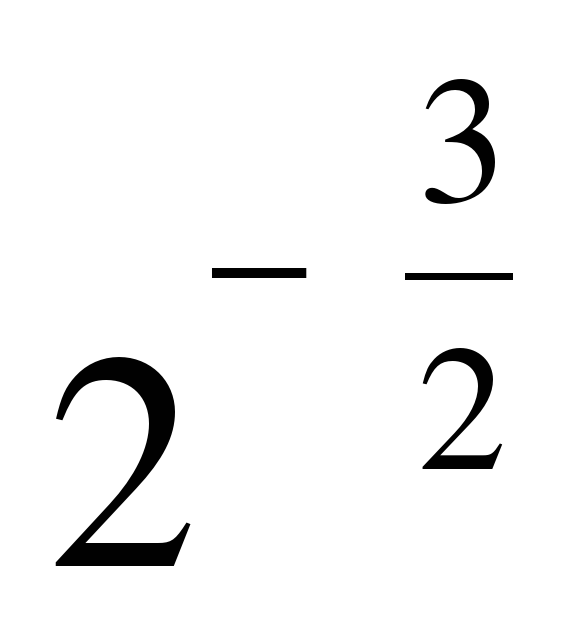 2) 2) 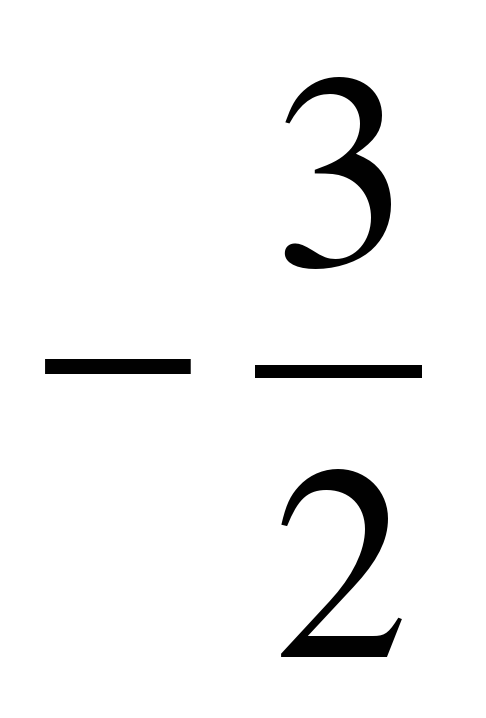 �� 3) 4�� 4)�� �� 3) 4�� 4)�� 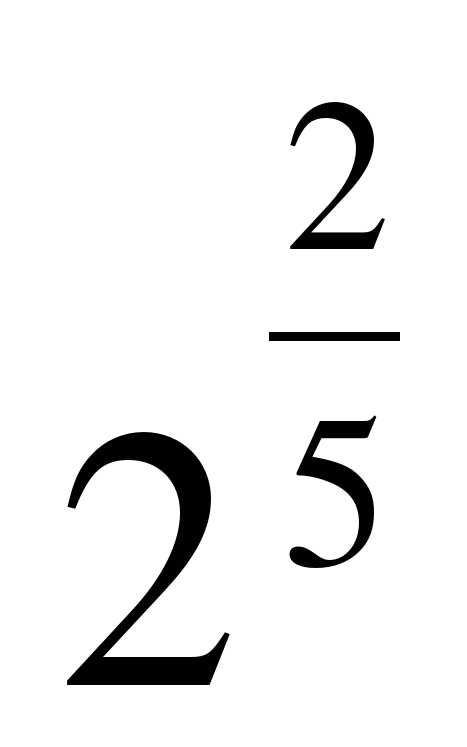 . . |
|
|
|
| A2
| Вычислите: ��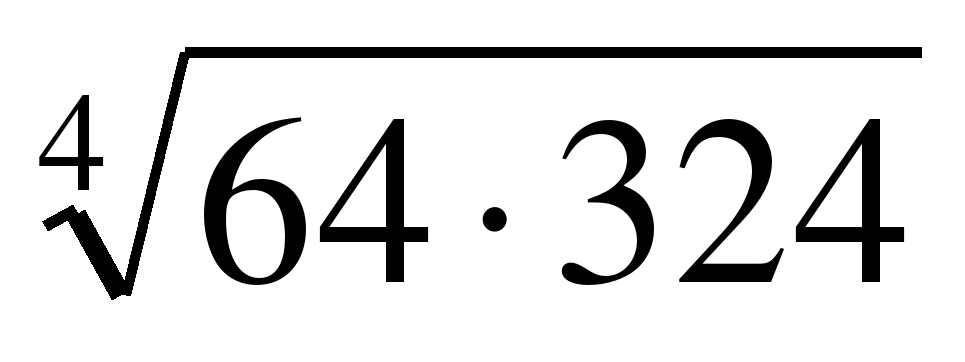 1) 12 2) 144 3) 72 4) 24 |
|
|
|
| A3
| Вычислите: ��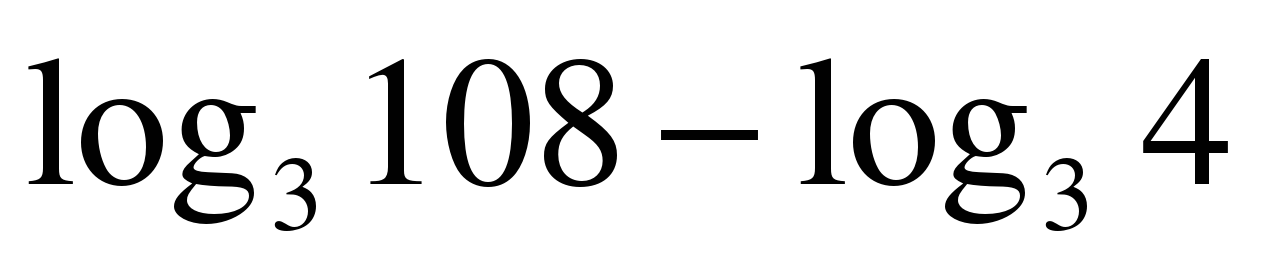 1) 27 2) 3 3) 9 4) ��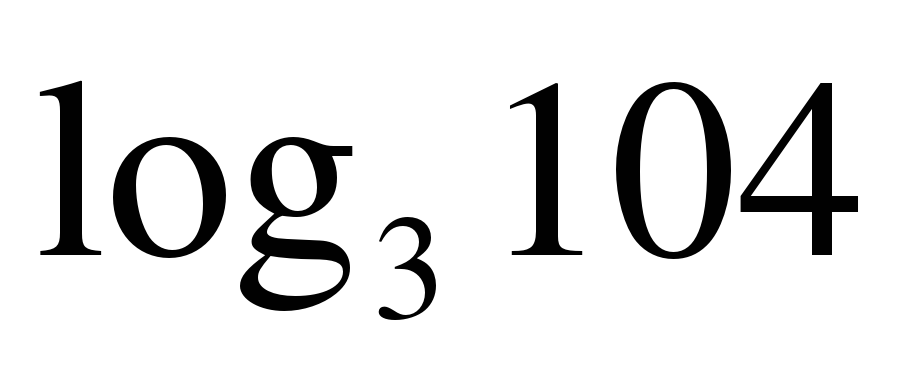 |
|
|
|
| A4
| На каком из следующих рисунков функция, заданная графиком, возрастает на промежутке [0;3] ?
|
|
| Найдите производную функции �� 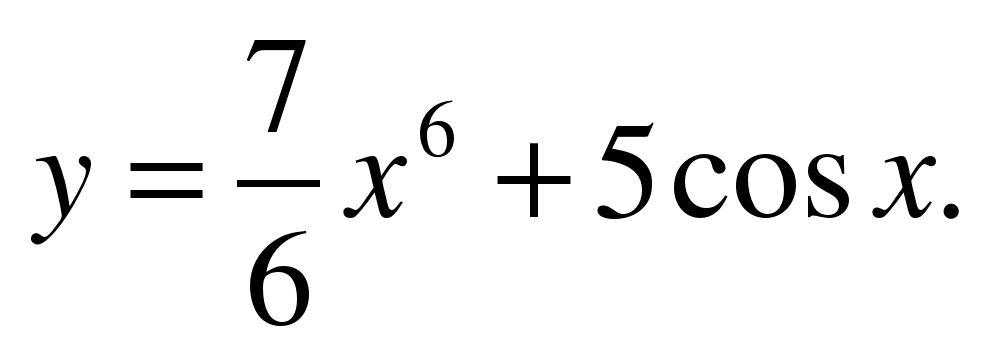 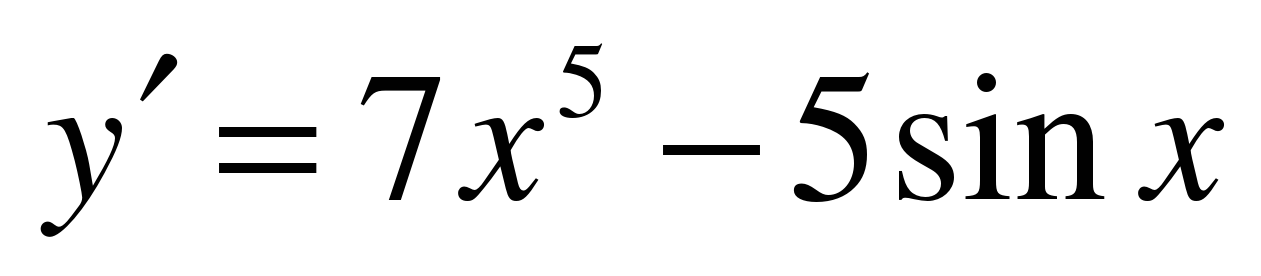 �� 3) �� 3) 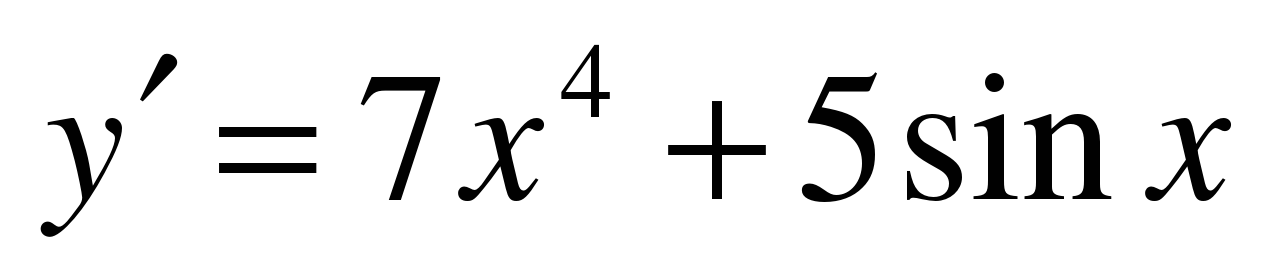 �� �� 2) ��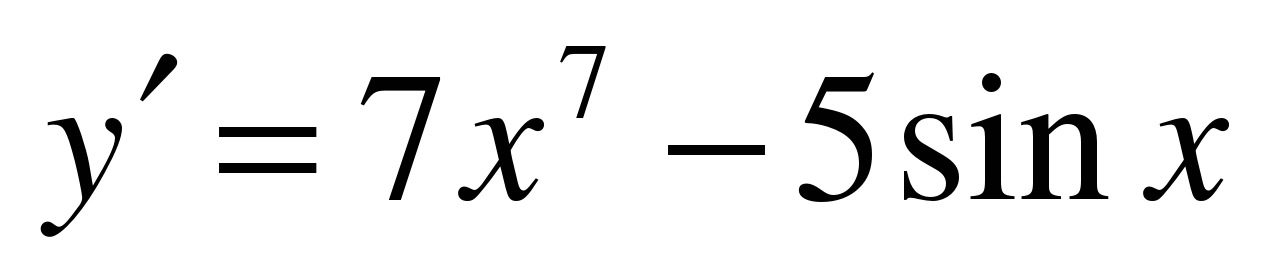 4) �� 4) ��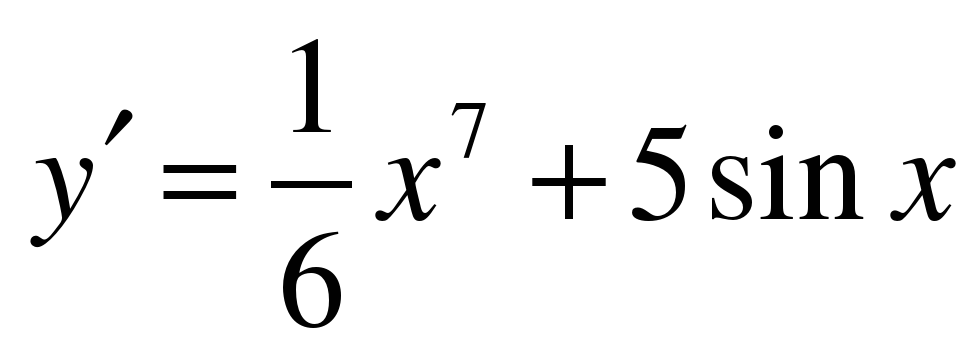
|
|
|
|
| A6 A5
| Найдите множество значений функции �� 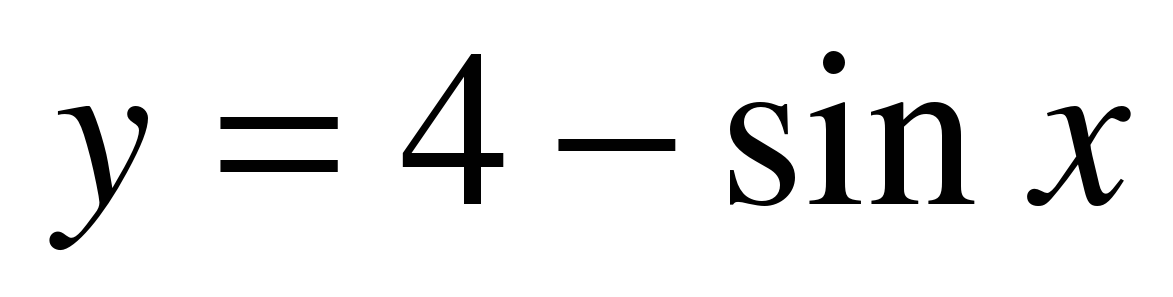 . . 1) [–1; 1] 2) [3; 5] 3) ��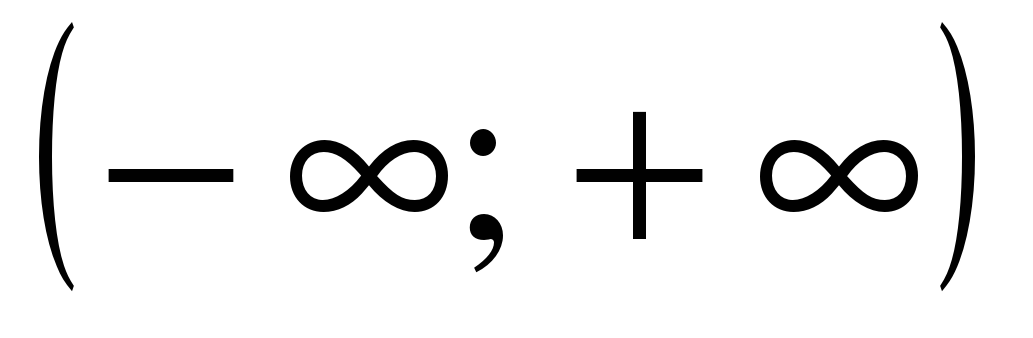 4) [3; 4]. 4) [3; 4].
|
|
|
|
| A7
| | Решите неравенство 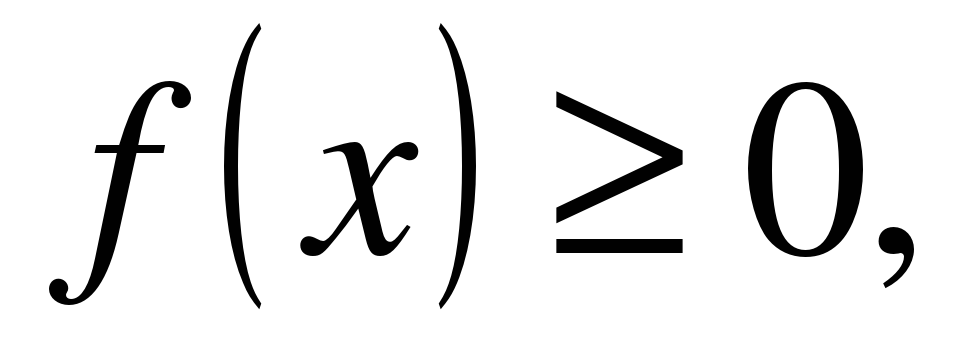 если на рисунке изображен график функции если на рисунке изображен график функции 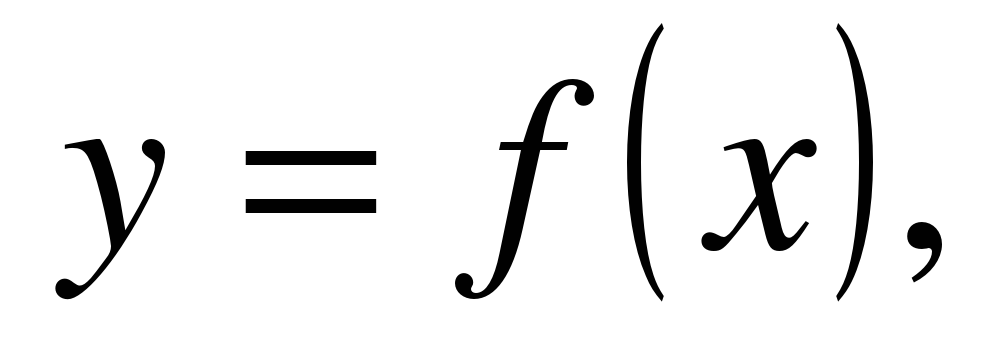 заданной на промежутке заданной на промежутке 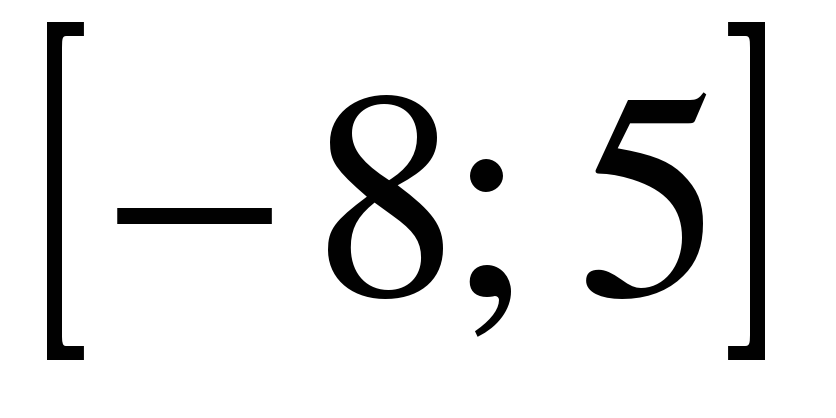 1) 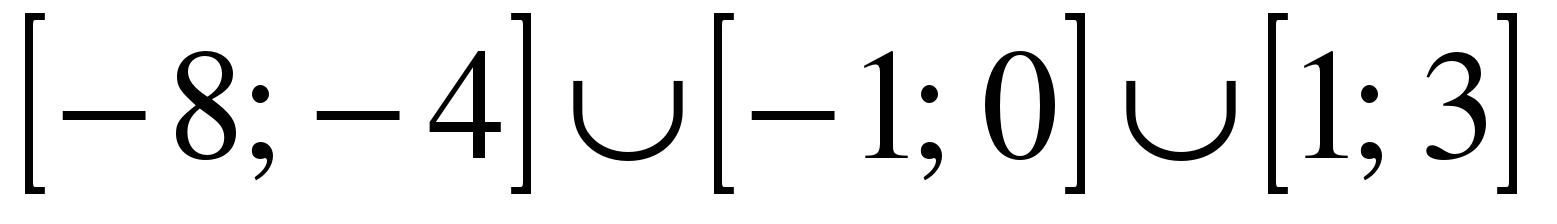 �� �� 2) 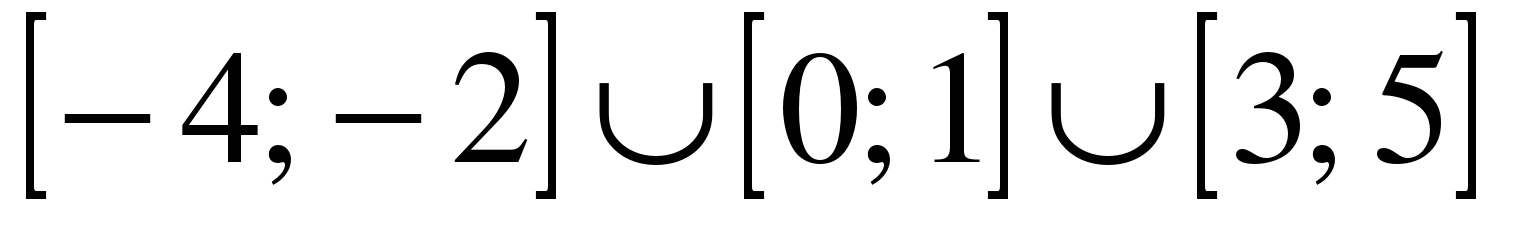 �� �� 3) 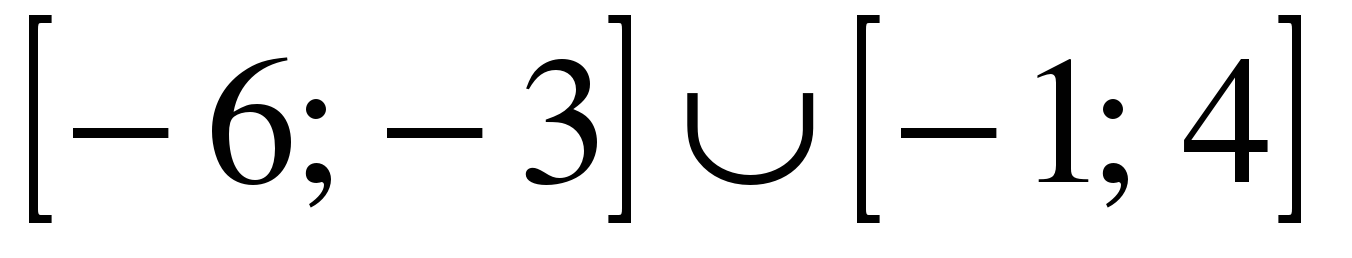 4) 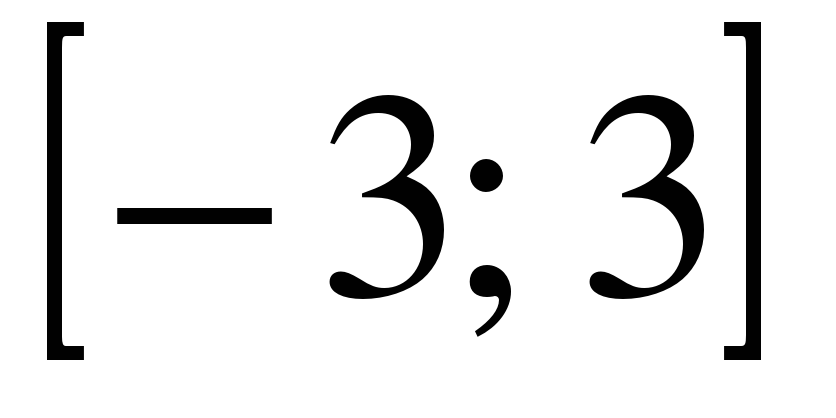 �� ��
| 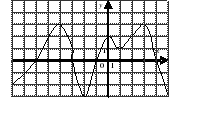 |
|
|
|
|
| A8
| Решите уравнение ��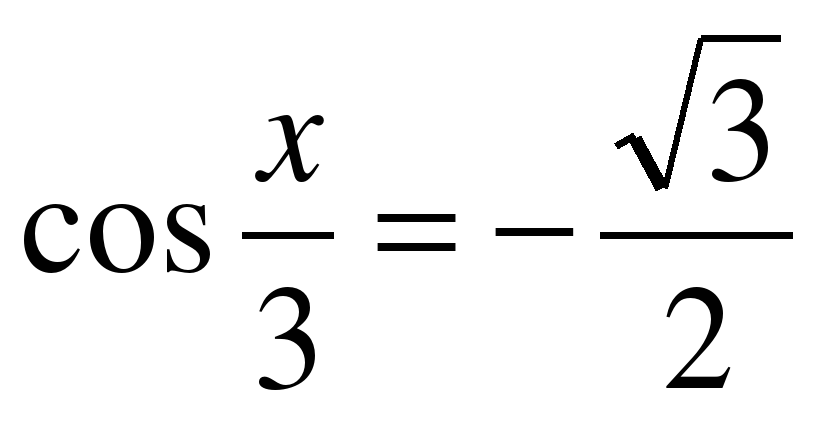 1) ��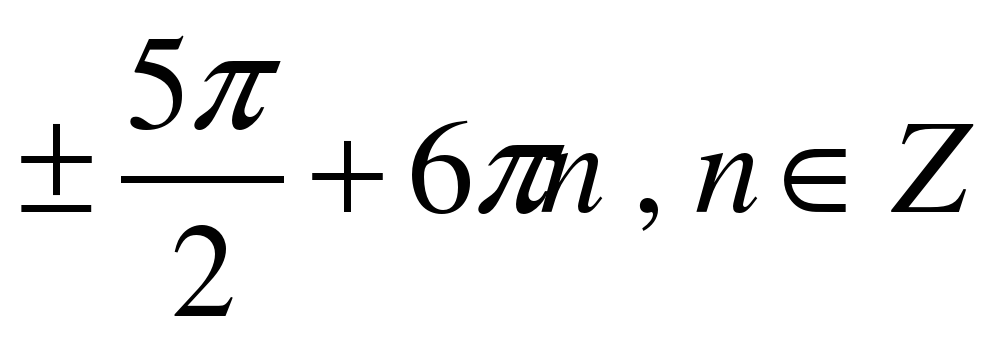 2) 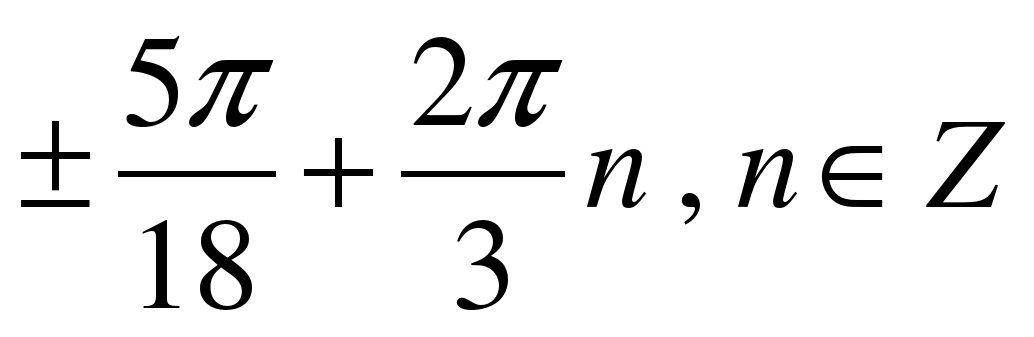 �� �� 3) ��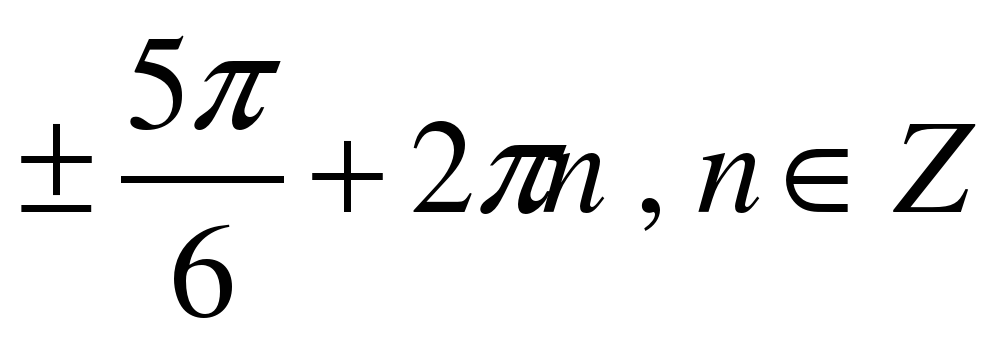 4) ��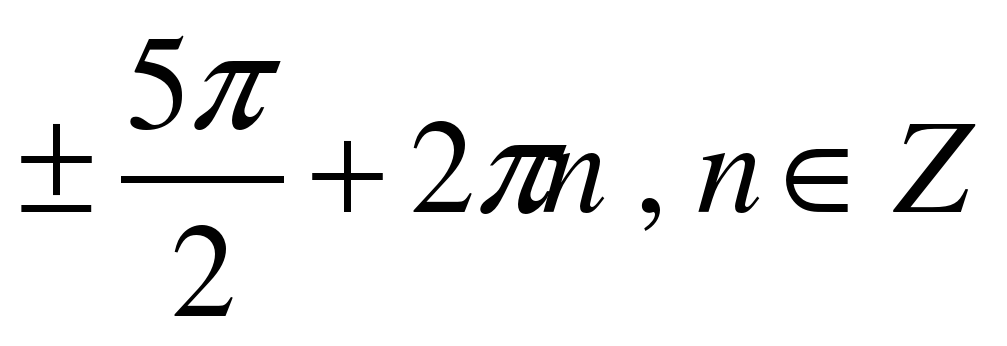
|
| A9
| Найдите область определения функции �� 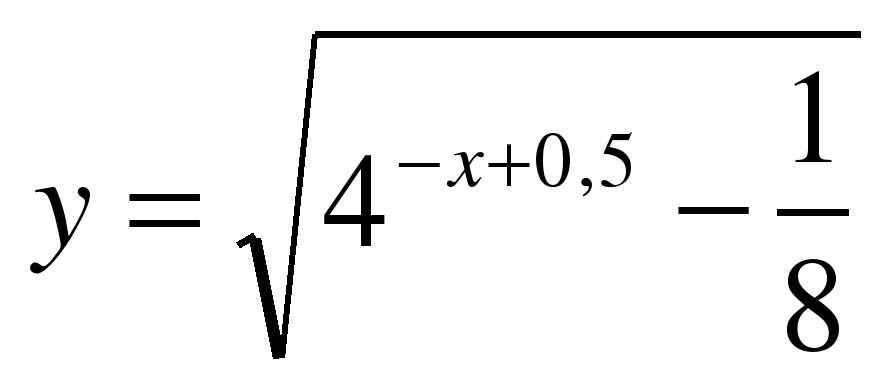 1) 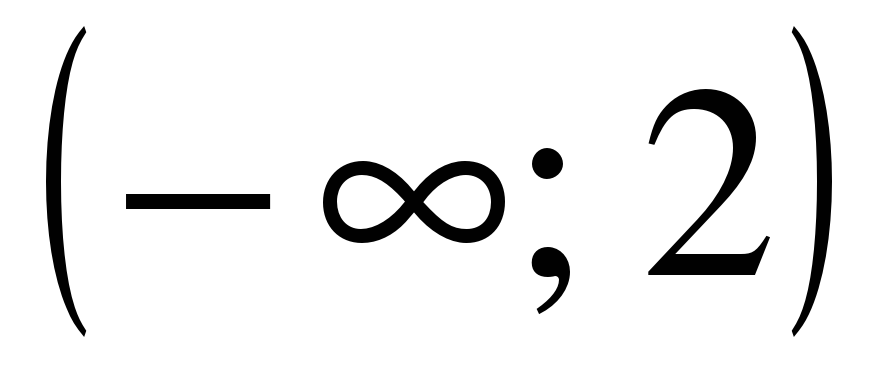 �� 2) �� �� 2) ��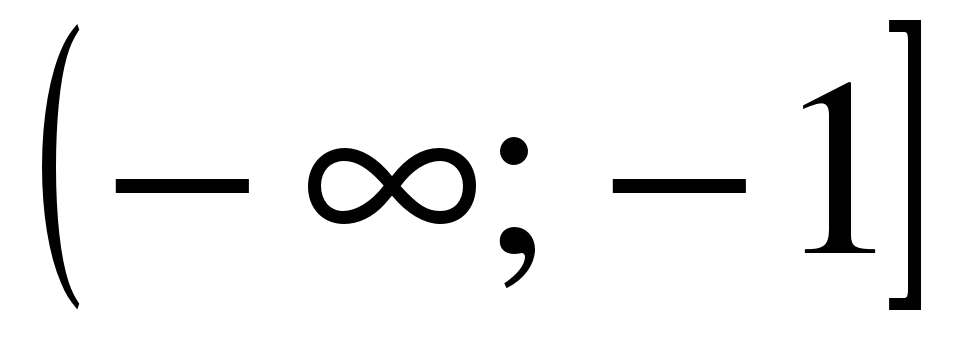 3) 3) 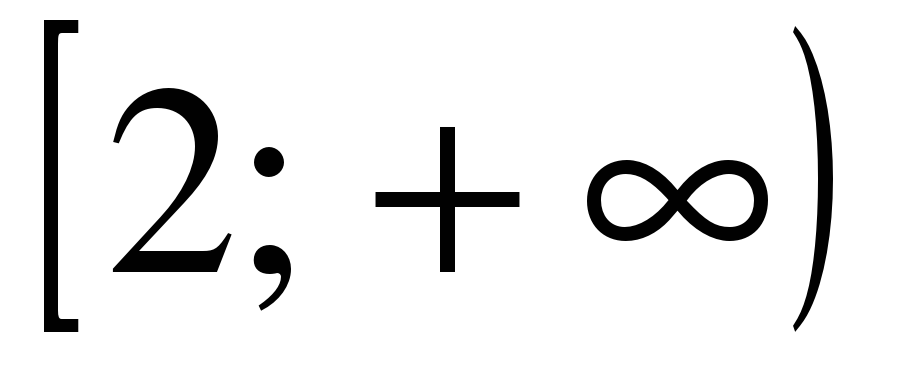 �� 4) �� 4) 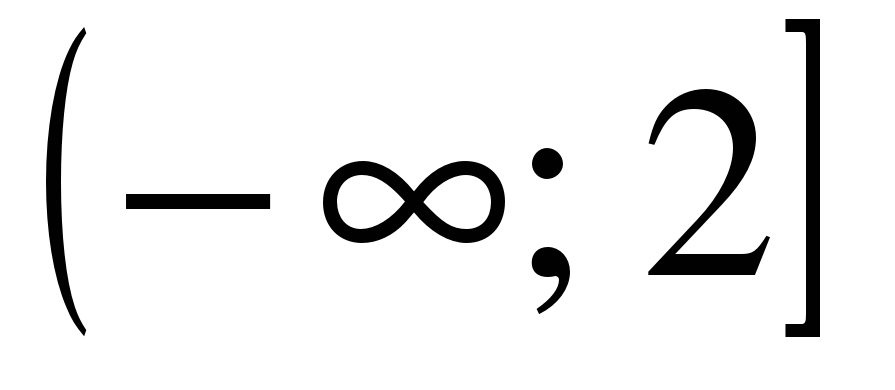 �� ��
|
|
|
|
|
| Решите неравенство ��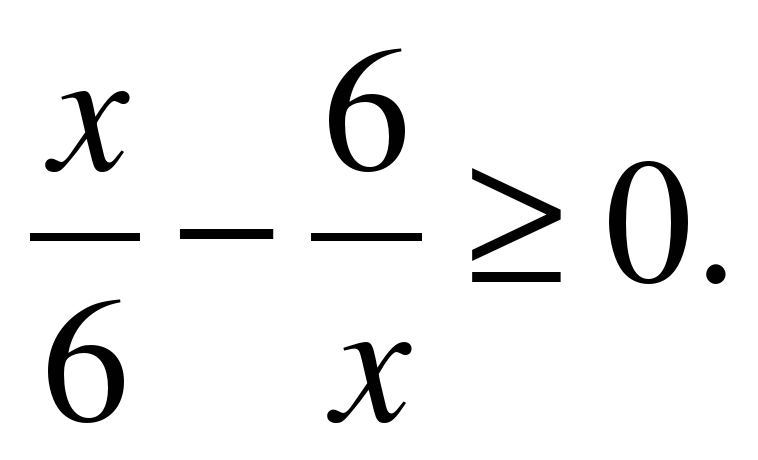 1) 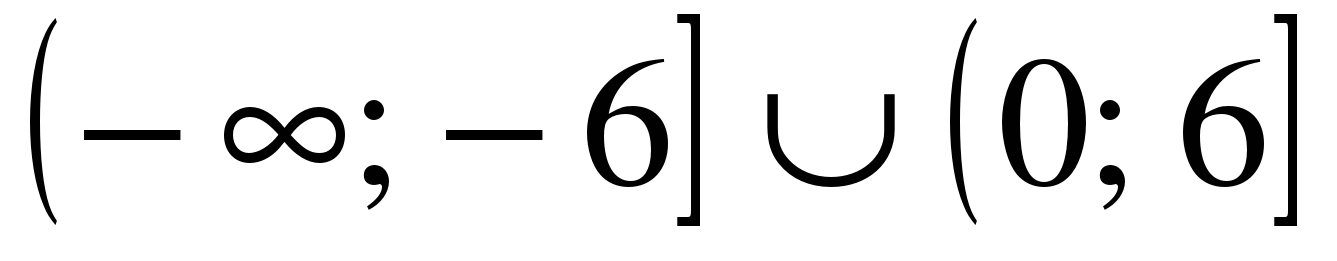 �� �� 2) ��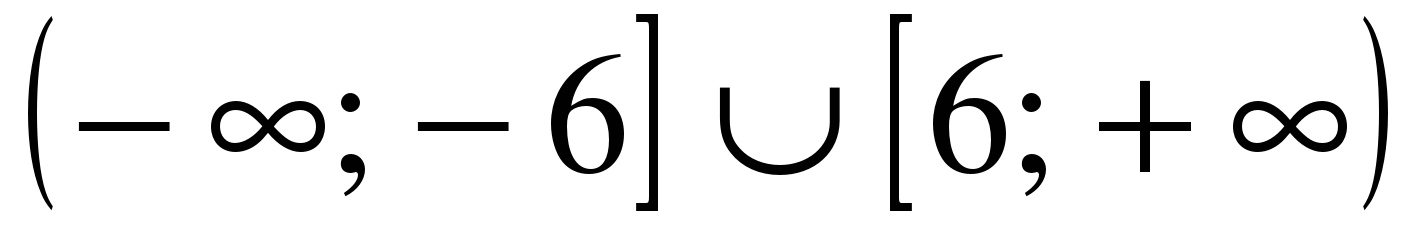 3) 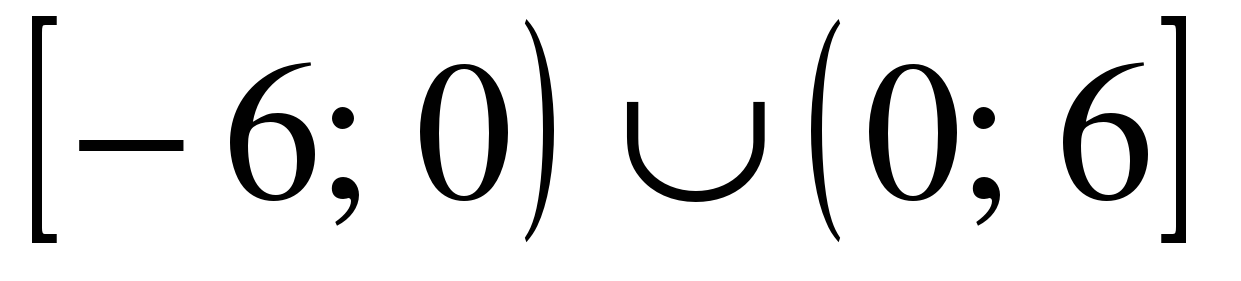 4) 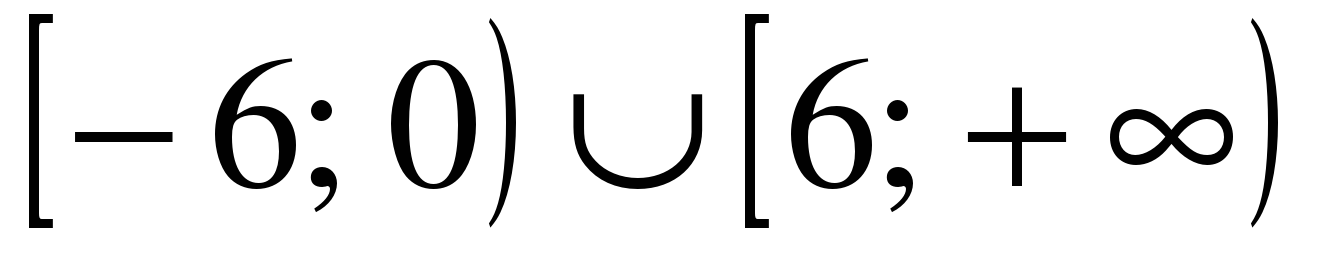 �� ��
|
A10
| Ответом на задания В1 – В11 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать
в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа
и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно. |
|
| Найдите значение выражения 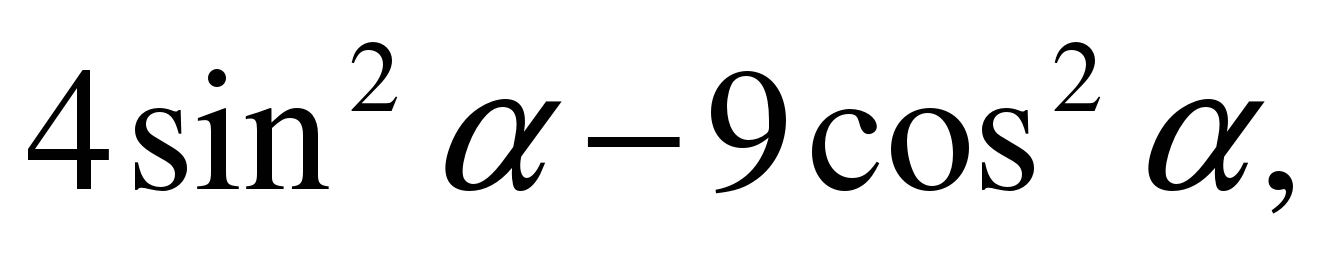 если если 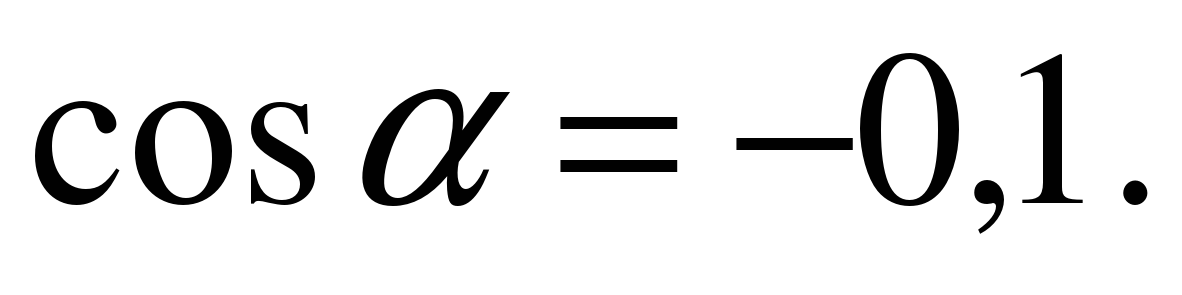
|
|
|
|
|
| Решите уравнение 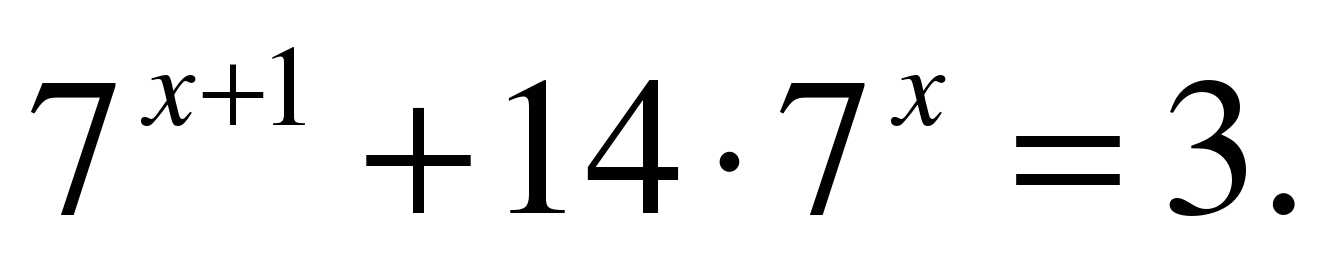 |
|
|
|
|
| Решите уравнение 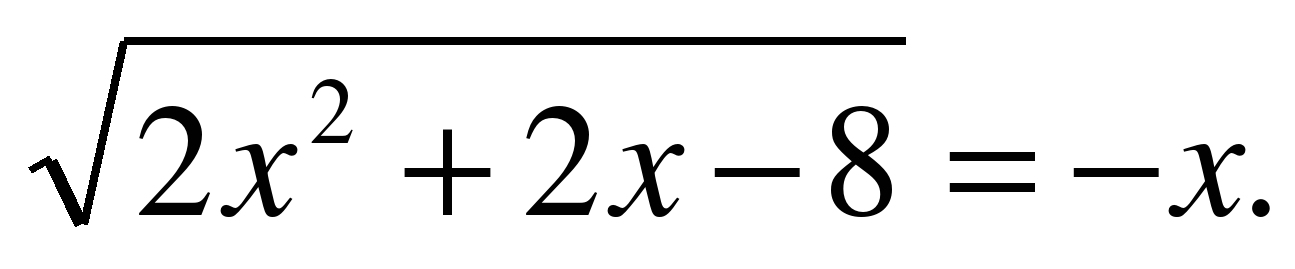 |
|
|
|
|
|
|
B1
B3
B5
B2
ЧАСТЬ 2
B4
|
| Вычислите значение выражения 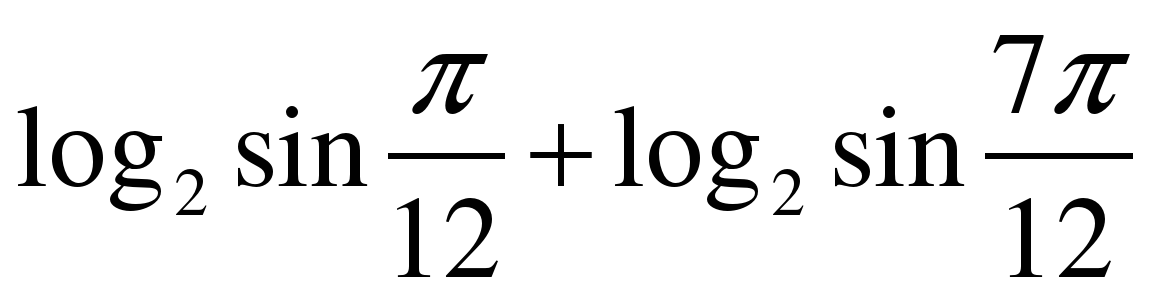 |
|
|
|
|
| Прямая, проходящая через начало координат, касается графика функции 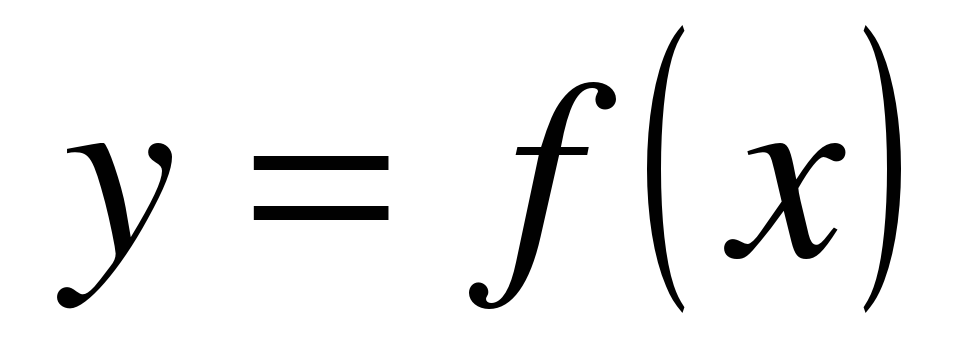 в точке в точке 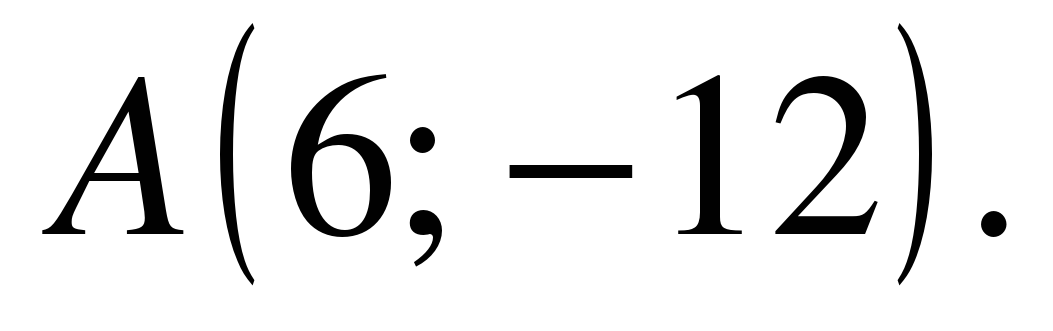 Найдите Найдите 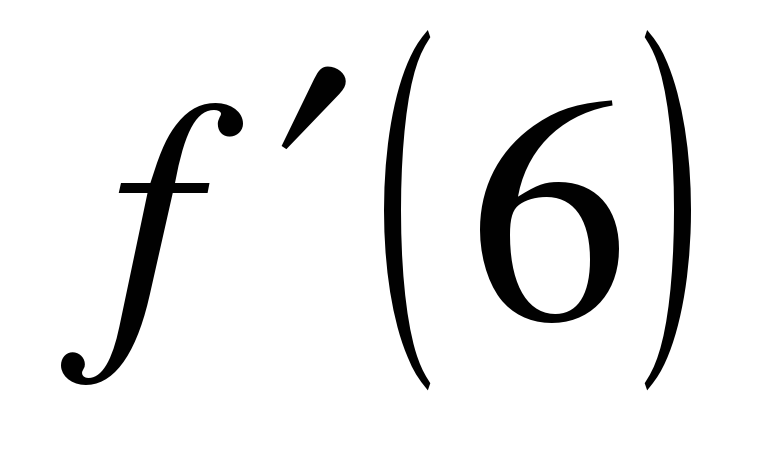 . .
|
|
|
|
|
| Найдите количество целочисленных решений неравенства удовлетворяющих неравенству
|
|
|
|
|
| Решите уравнение
|
|
|
|
|
| Функция 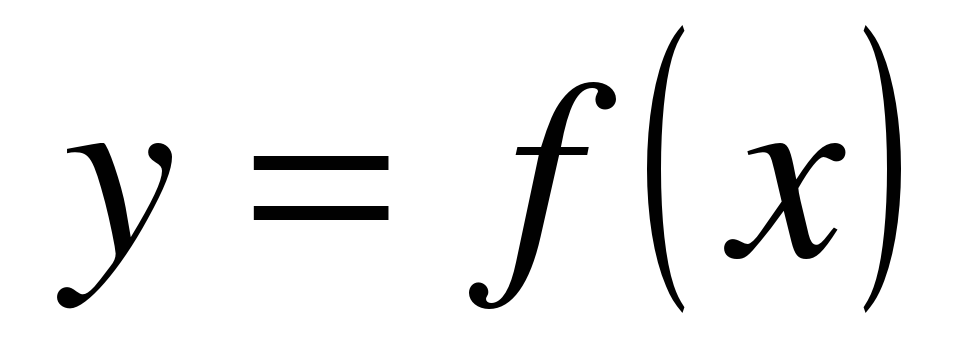 определена на всей числовой прямой и является четной периодической функцией с периодом, равным 6. На отрезке функция задана формулой Определите количество нулей этой функции на отрезке . определена на всей числовой прямой и является четной периодической функцией с периодом, равным 6. На отрезке функция задана формулой Определите количество нулей этой функции на отрезке .
|
*B9
|
|
|
|
| Цену товара повысили на 25%. На сколько процентов требуется уменьшить полученную цену товара, чтобы она стала равной первоначальной цене?
|
*B10
Боковое ребро прямой призмы ABCA1B1C1 равно 16. Основание призмы – треугольник АВС, площадь которого равна 4, ВС = 3. Найдите тангенс угла между плоскостями А1ВС и АВС.
B6
B7
B8
*B11
В параллелограмме ABCD биссектриса угла В пересекает сторону CD в точке Т и прямую AD в точке М. Найдите периметр треугольника СВТ, если АВ = 21, ВМ = 35, MD = 9.
| Для записи ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем решение. |
C1
|
| Найдите точки максимума функции
|
|
| Решите уравнение |
|
|
ЧАСТЬ 3
|
|
| | Для записи ответов на задания (С3 – С5) используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем обоснованное решение. |
|
|
|
|
C3
|
| Найдите все значения а, для каждого из которых найдется х из промежутка [0; 2) такое, что значение выражения равно значению выражения
|
|
|
|
*C4
|
| Дана сфера диаметром 26. Сечением сферы плоскостью, удаленной от центра сферы на расстояние 5, является окружность с диаметром АВ. Точка D выбрана на сфере, а точка С – на окружности сечения так, что объем пирамиды DABC наибольший. Найдите площадь треугольника DMN, где M и N – середины ребер АС и ВС соответственно.
|
|
|
|
|
| Решите уравнение , если известно, что и |
C2
C5
8
Просмотр содержимого документа
«Математика_16вариант»
Просмотр содержимого документа
«Математика_17вариант»
Просмотр содержимого документа
«Математика_18вариант»
Репетиционный ЕГЭ по МАТЕМАТИКЕ 2008 г.
Вариант № 18
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается
4 часа (240 мин). Работа состоит из трех частей и содержит 26 заданий.
Часть 1 содержит 13 заданий (А1 – А10 и В1 – В3) обязательного уровня по материалу курса «Алгебра и начала анализа» 10-11 классов.
К каждому заданию А1 – А10 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ.
Часть 2 содержит 10 более сложных заданий (В4 – В11, С1, С2) по материалу курса «Алгебра и начала анализа» 10-11 классов, а также различных разделов курсов алгебры и геометрии основной и средней школы. К заданиям В4 – В11 надо дать краткий ответ, к заданиям С1 и С2 – записать решение.
Часть 3 содержит 3 самых сложных задания, два – алгебраических
(С3, С5) и одно – геометрическое (С4). При их выполнении надо записать обоснованное решение.
За выполнение работы выставляются две оценки: аттестационная отметка и тестовый балл. Аттестационная отметка за усвоение курса алгебры и начал анализа 10-11 классов выставляется по пятибалльной шкале. При ее выставлении не учитывается выполнение четырех заданий (В9, В10, В11, С4). В тексте работы номера этих заданий отмечены звездочкой.
Тестовый балл выставляется по 100-балльной шкале на основе первичных баллов, полученных за выполнение всех заданий работы.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха!
ЧАСТЬ 1
| При выполнении заданий А1 – А10 в бланке ответов № 1 под номером выполняемого задания поставьте знак "´" в клеточке, номер которой соответствует номеру выбранного вами ответа. |
| A1
| Найдите значение выражения �� 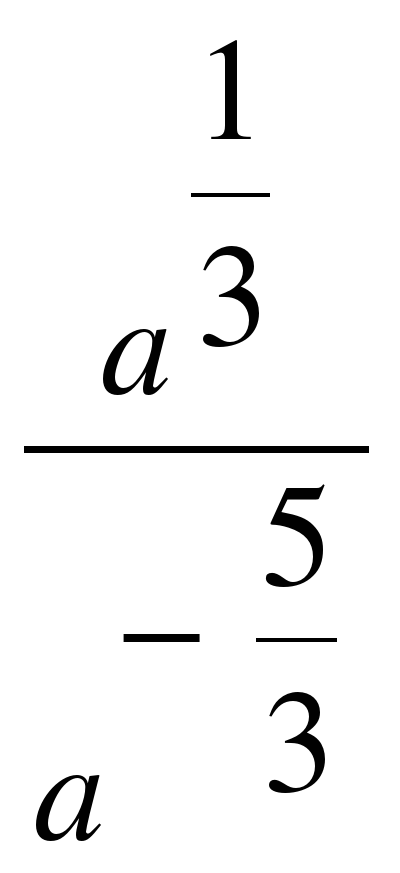 при a = 3 при a = 3 1) 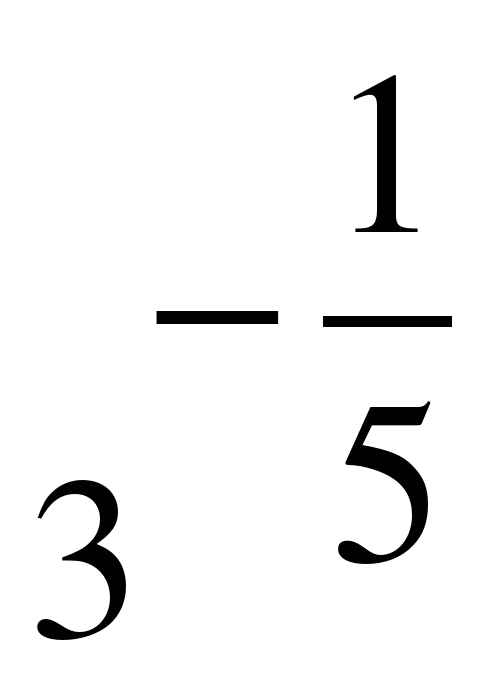 2) 2) 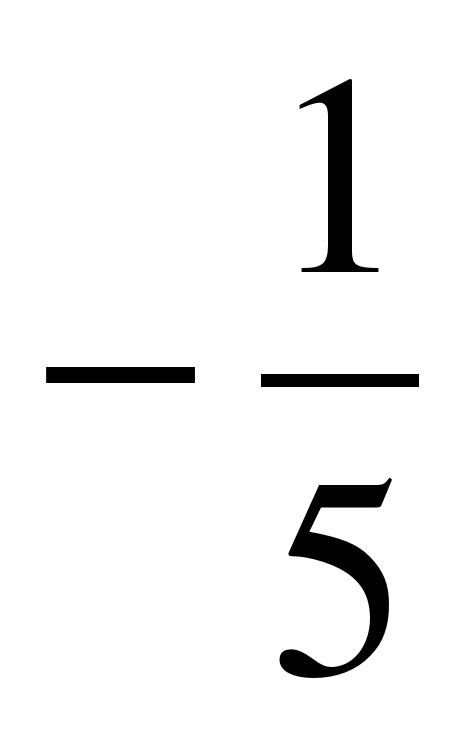 3) 9�� 4)�� 3) 9�� 4)�� 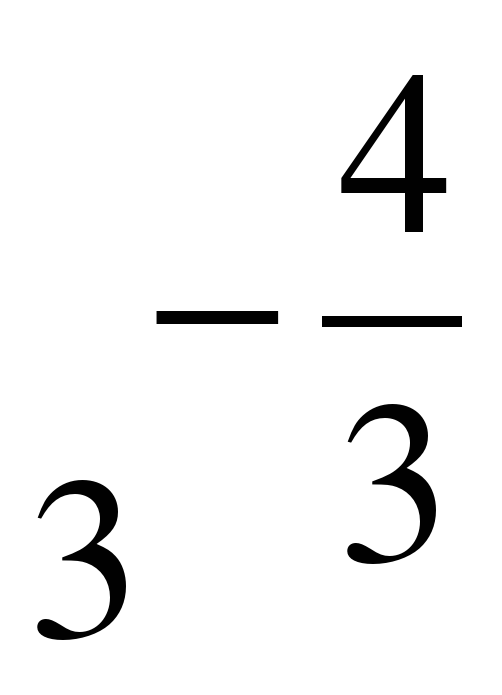
|
|
|
|
| A2
| Вычислите: ��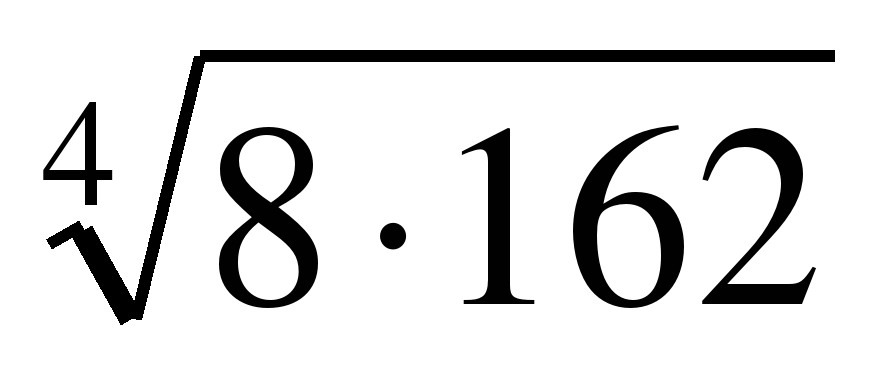 1) 12 2) 36 3) 18 4) 6 |
|
|
|
| A3
| Вычислите: ��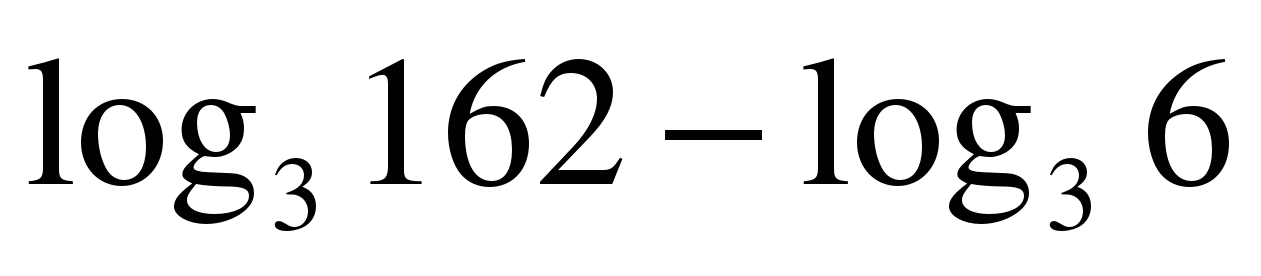 1) 9 2) 27 3) 3 4) ��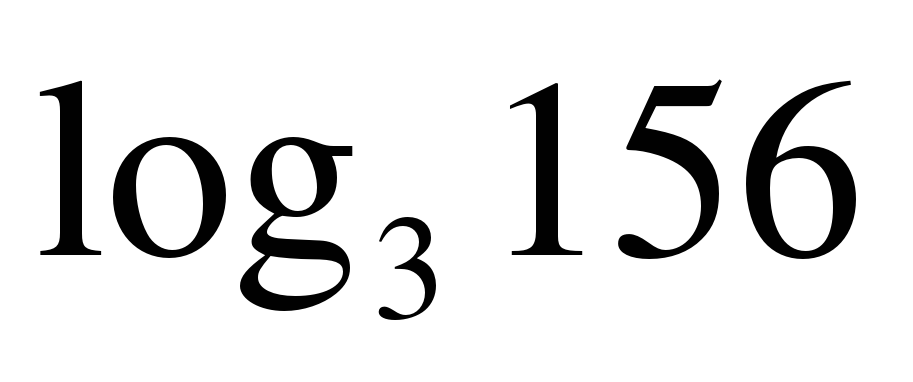
|
|
|
|
| A4
| На каком из следующих рисунков функция, заданная графиком, убывает на промежутке [0;3] ?
|
| A5
| Найдите производную функции �� 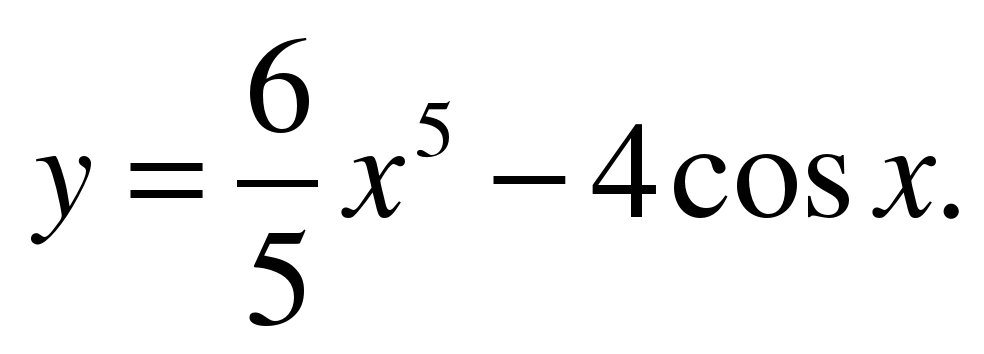 ��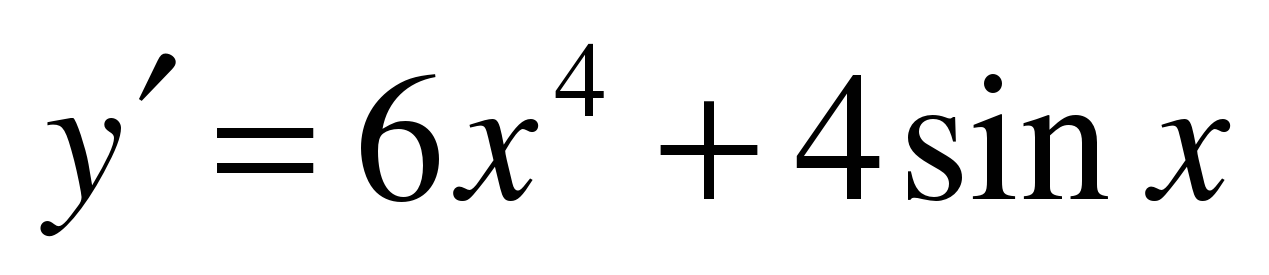 3) �� 3) ��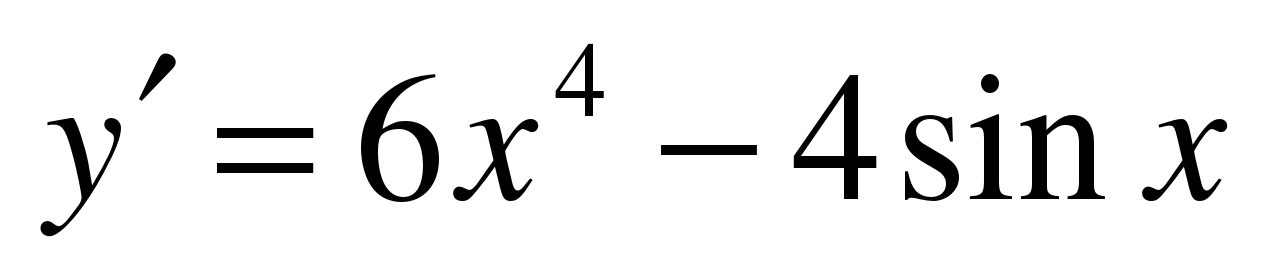  ��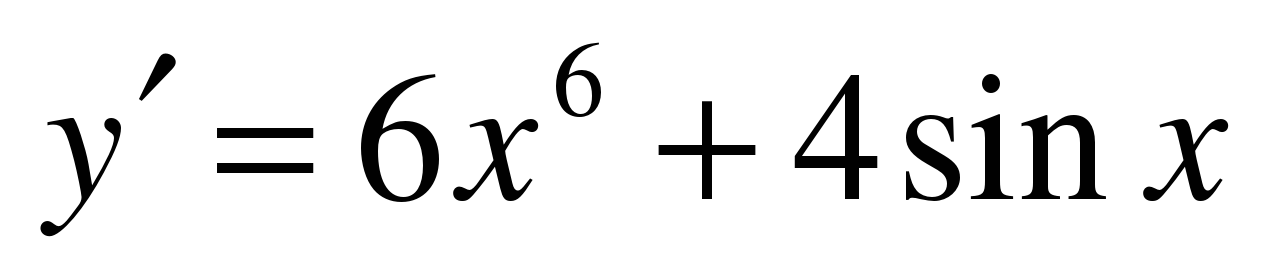 4) �� 4) ��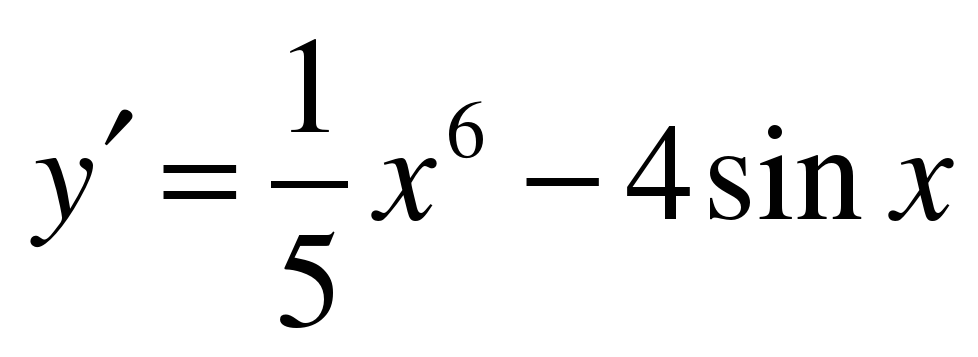
|
|
|
|
| A6
| Найдите множество значений функции �� 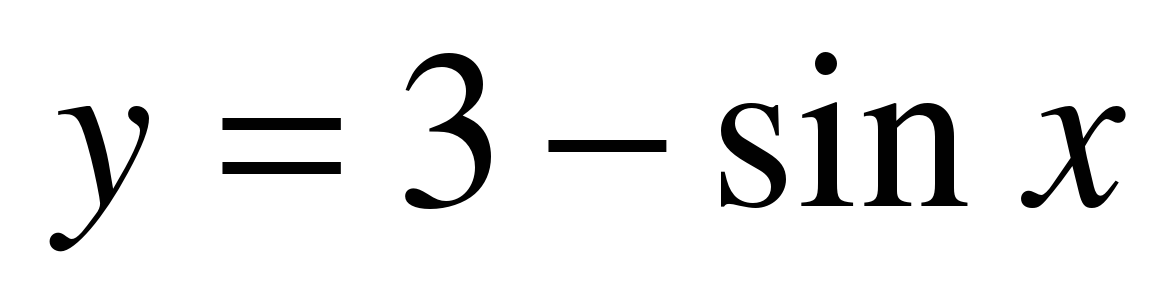 . . 1) [2; 3]. 2) [–1; 1] 3) ��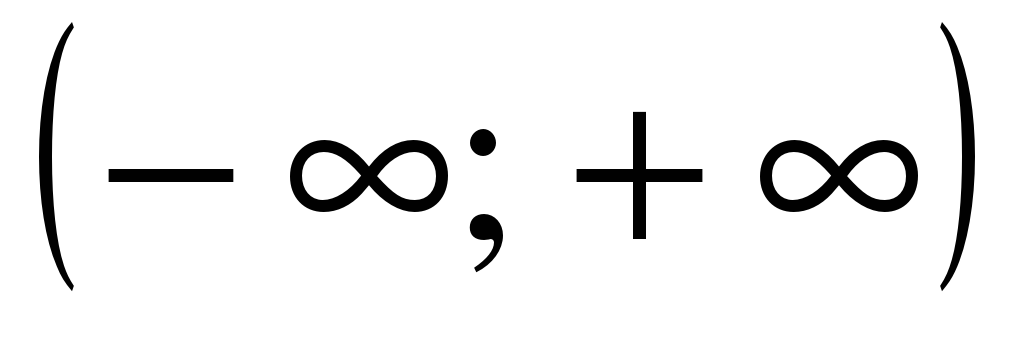 4) [2; 4] 4) [2; 4]
|
|
|
|
| A7
| | Решите неравенство 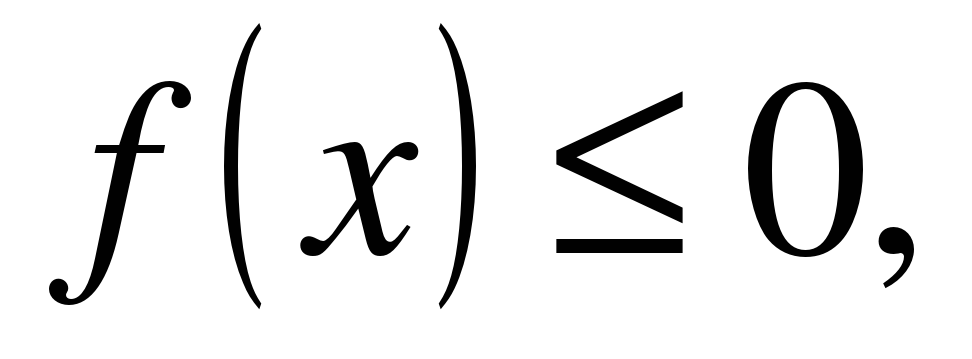 если на рисунке изображен график функции если на рисунке изображен график функции 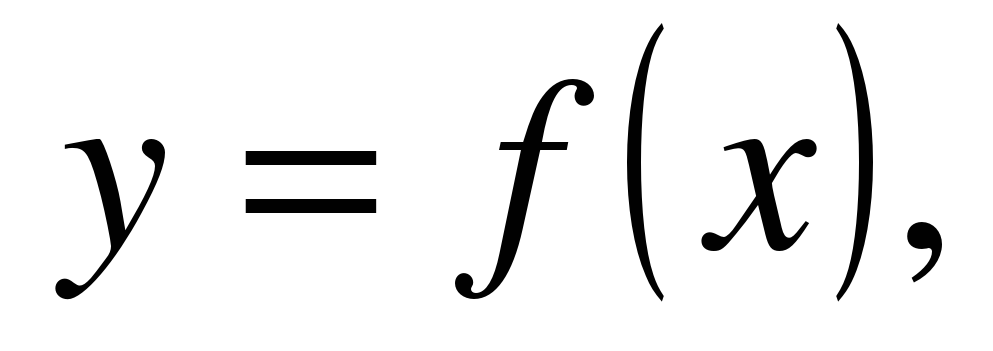 заданной на промежутке заданной на промежутке 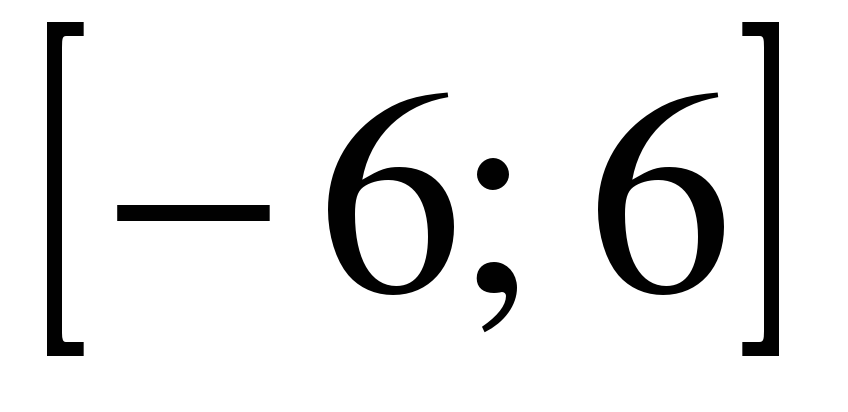 1) 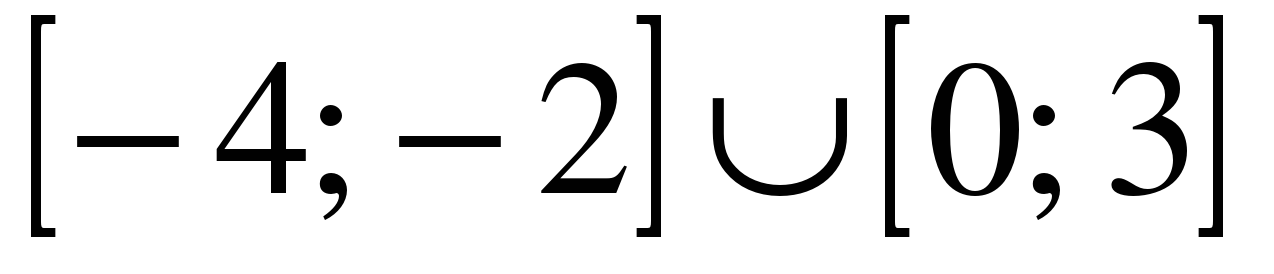 �� �� 2) 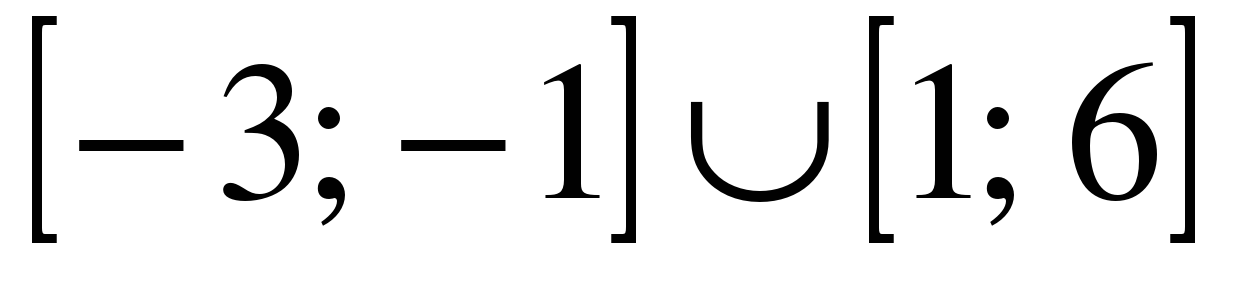 �� �� 3) 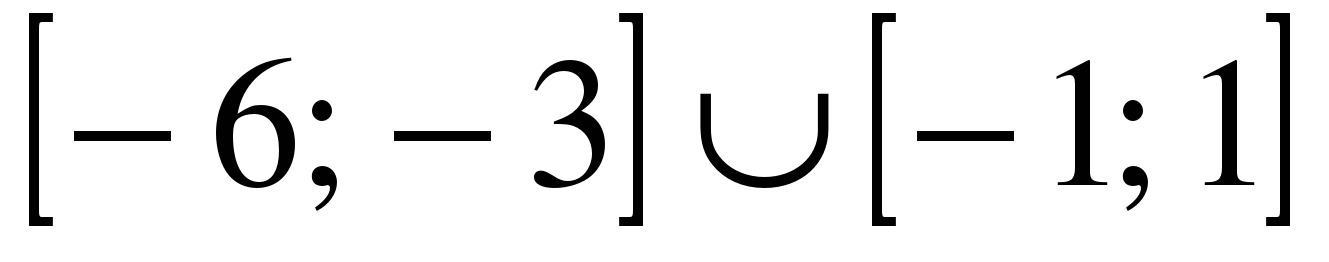 4) 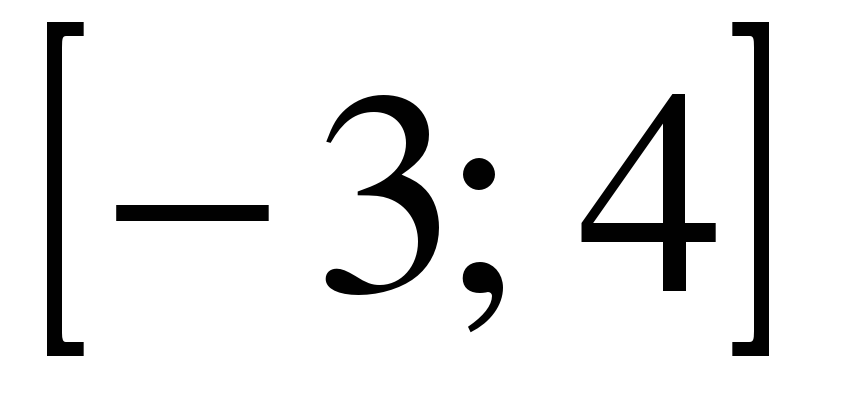 �� �� | 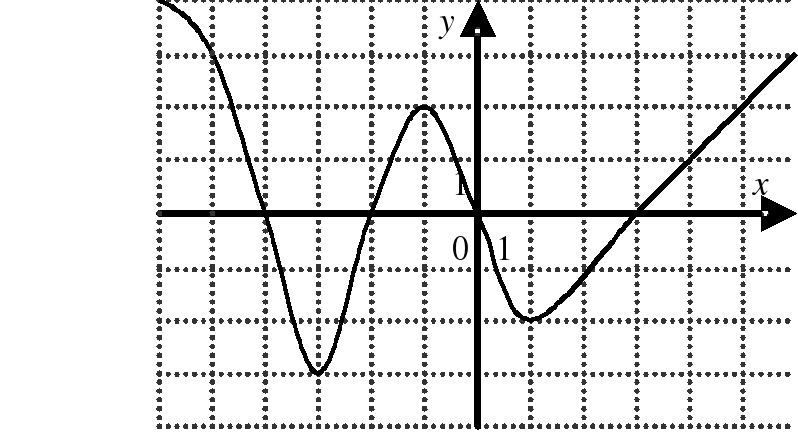 |
|
|
|
|
| A8
| Решите уравнение ��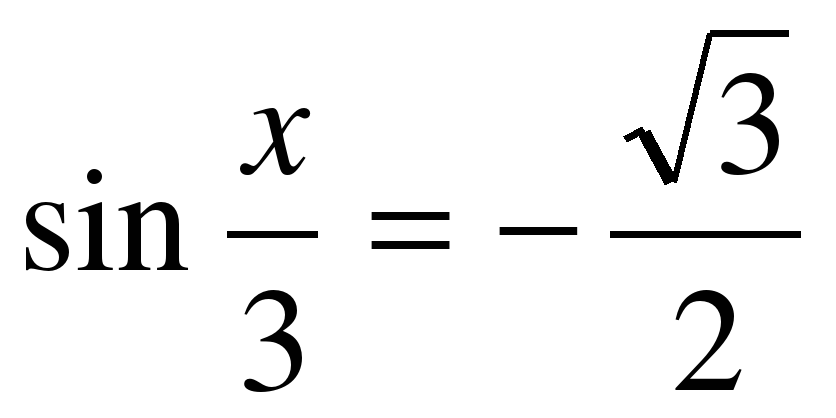 1) ��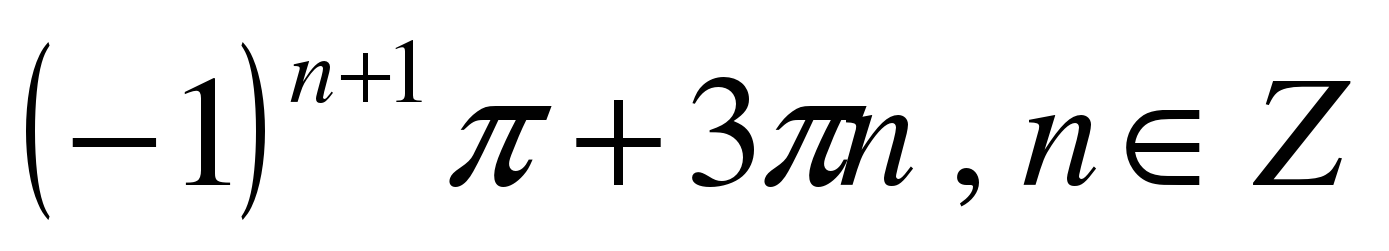 2) ��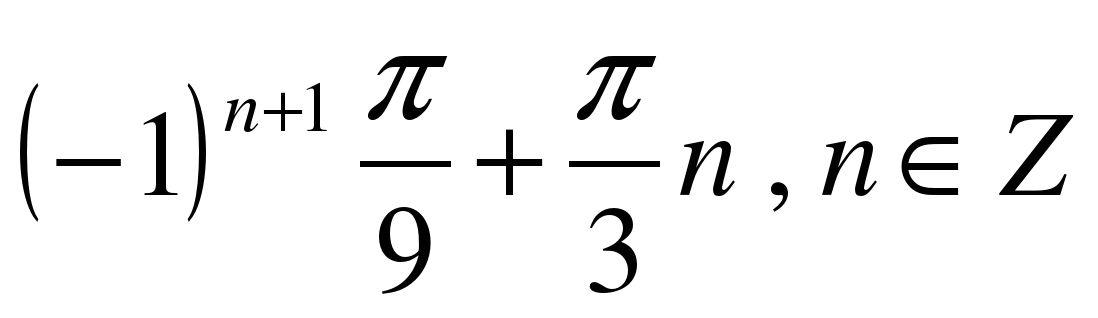 3) ��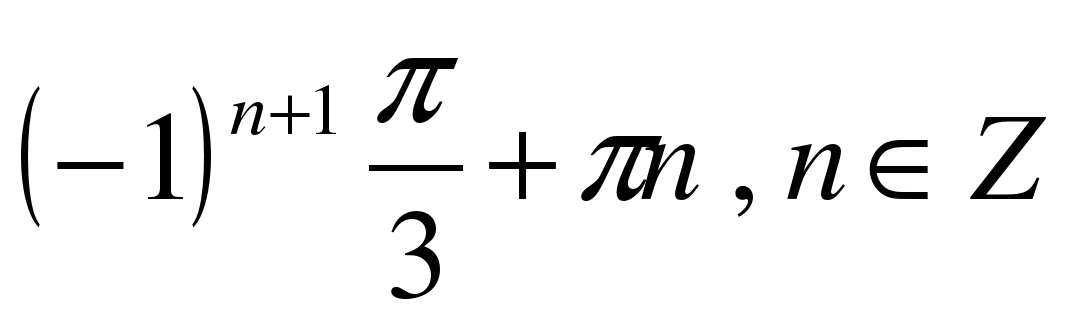 4) ��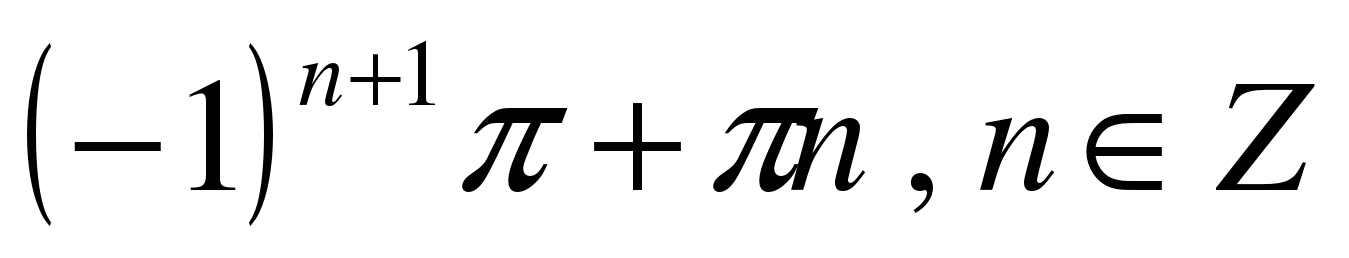
|
| A9
| Найдите область определения функции �� 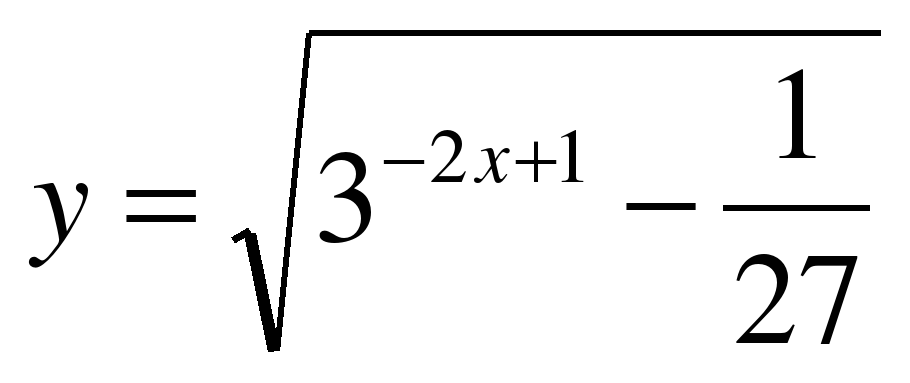 1) 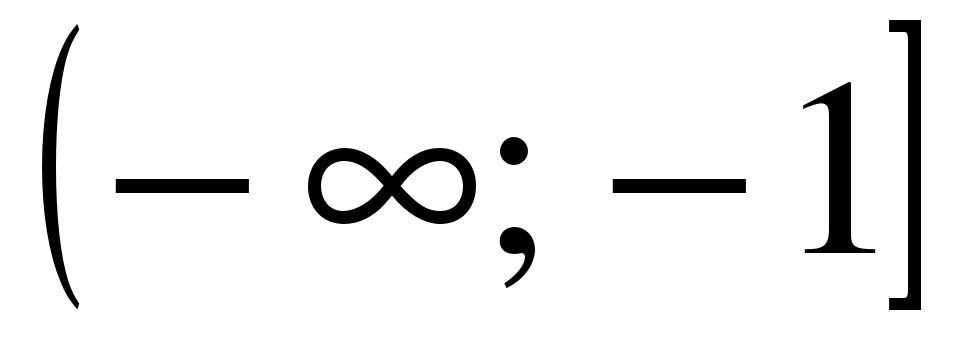 �� 2) �� 2) 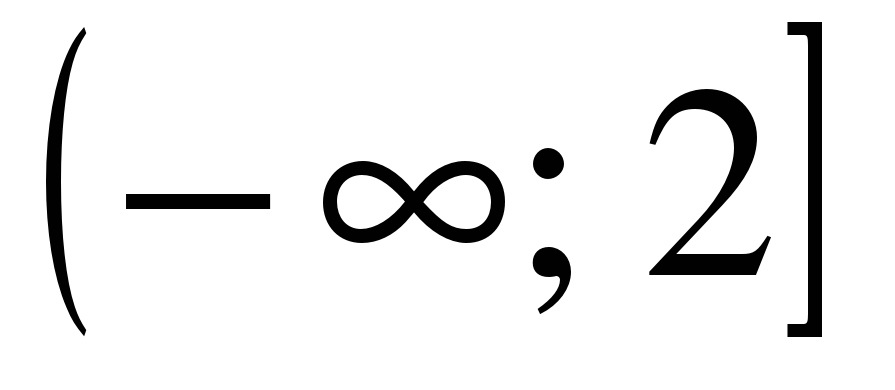 �� 3) �� 3) 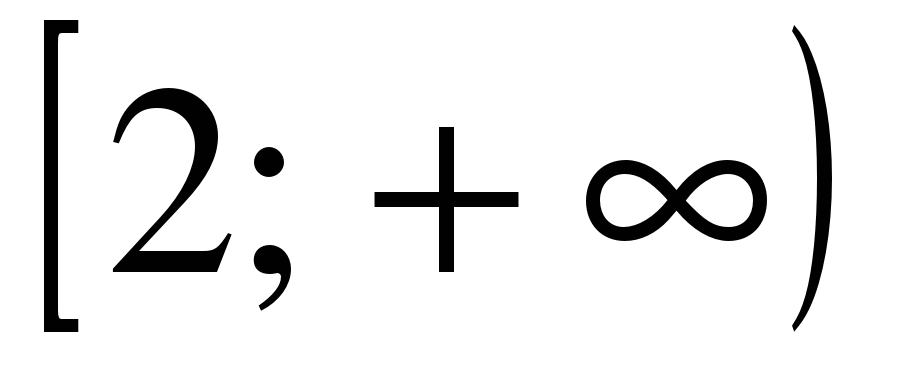 �� 4) �� �� 4) ��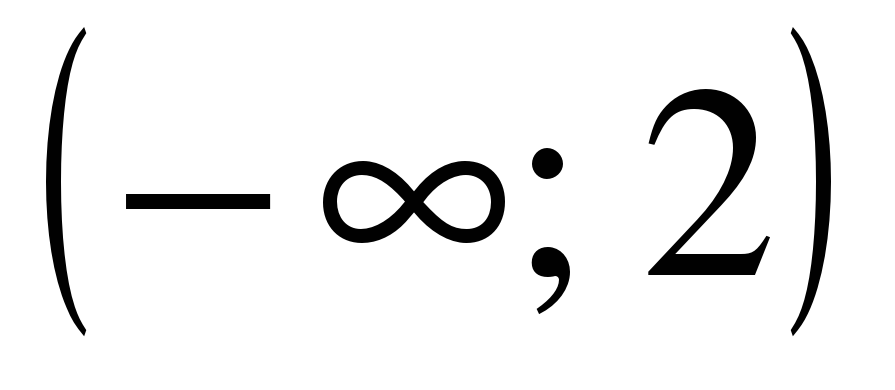
|
|
|
|
|
| Решите неравенство ��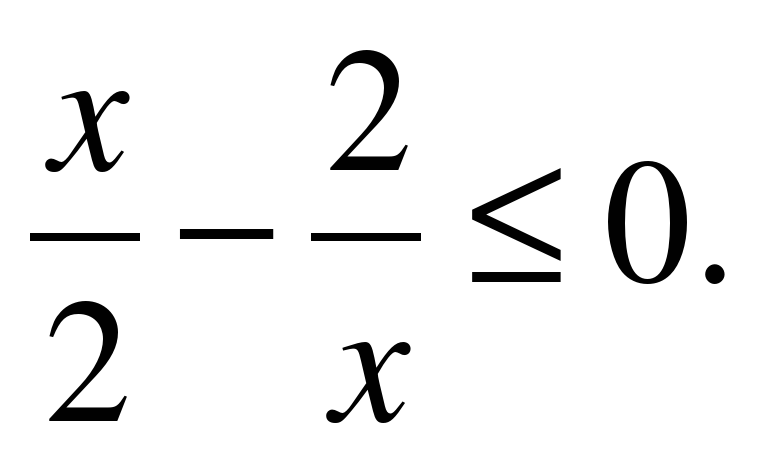 1) 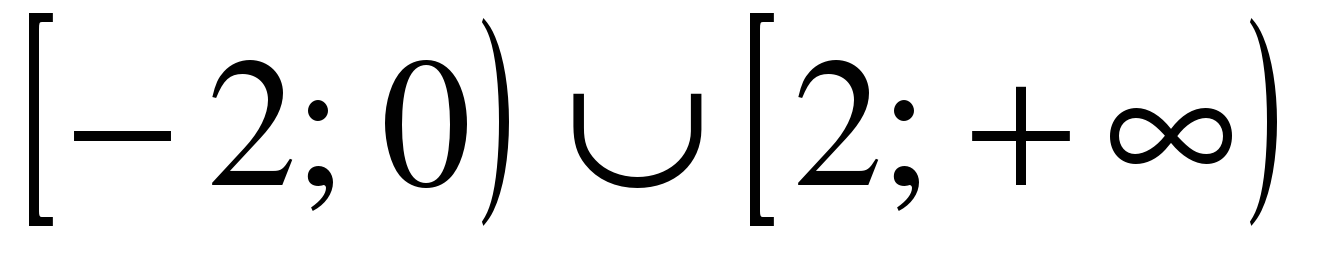 �� �� 2) ��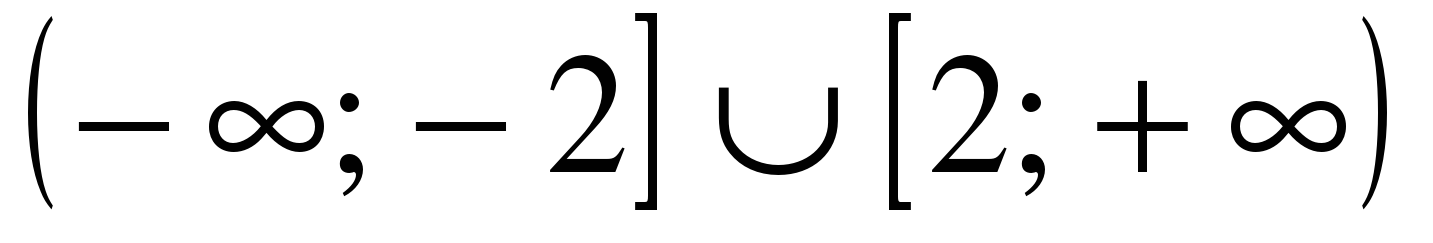 3) 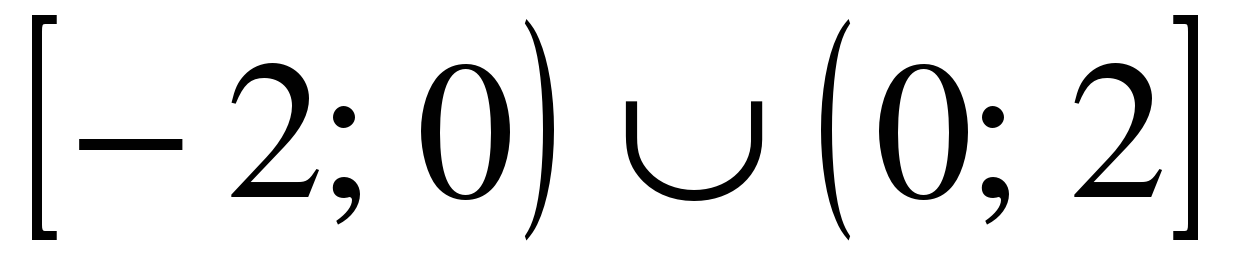 4) 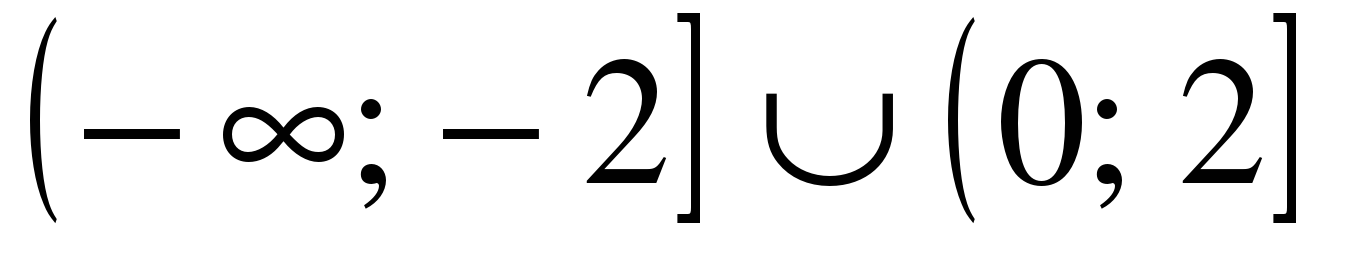 �� �� |
A10
| Ответом на задания В1 – В11 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать
в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа
и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно. |
|
| Найдите значение выражения 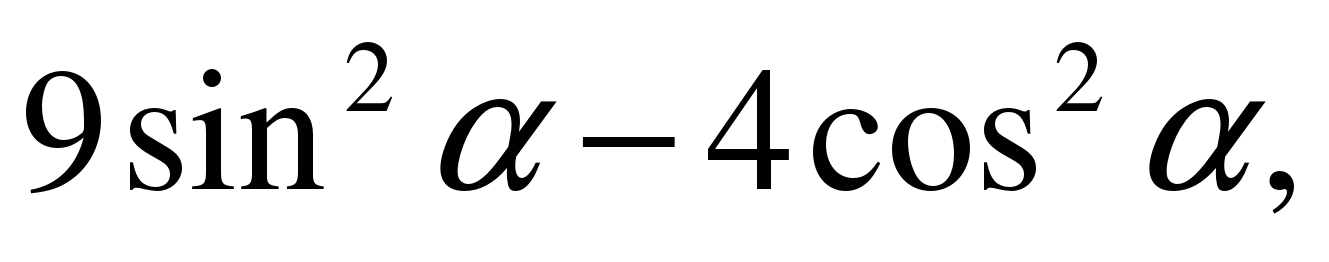 если если 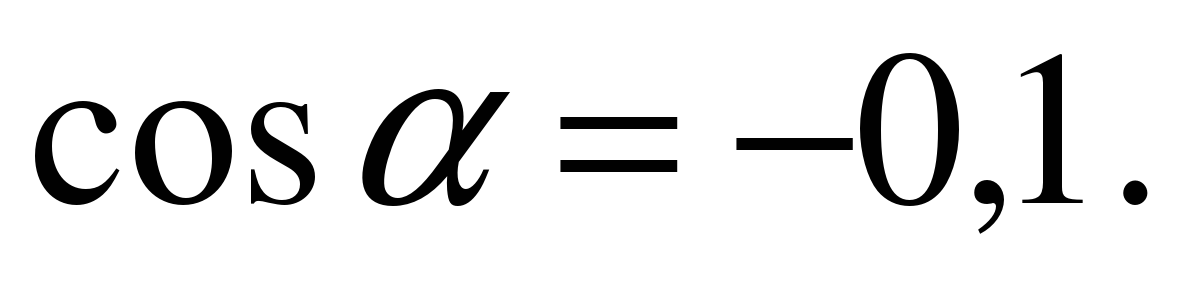
|
|
|
|
|
| Решите уравнение 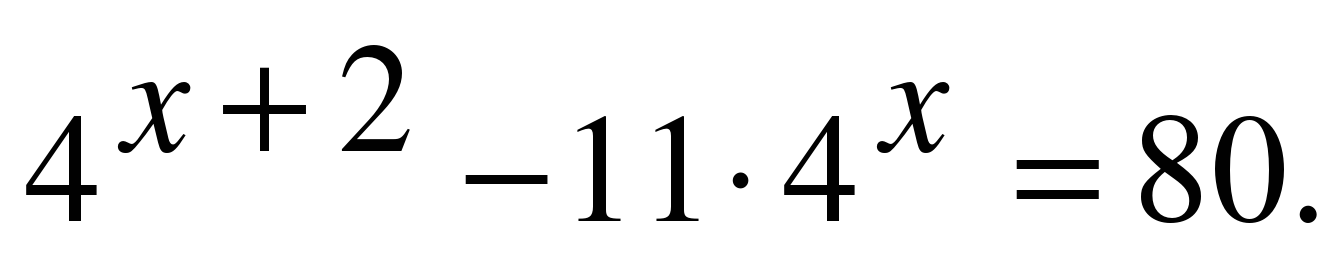
|
|
|
|
|
| Решите уравнение 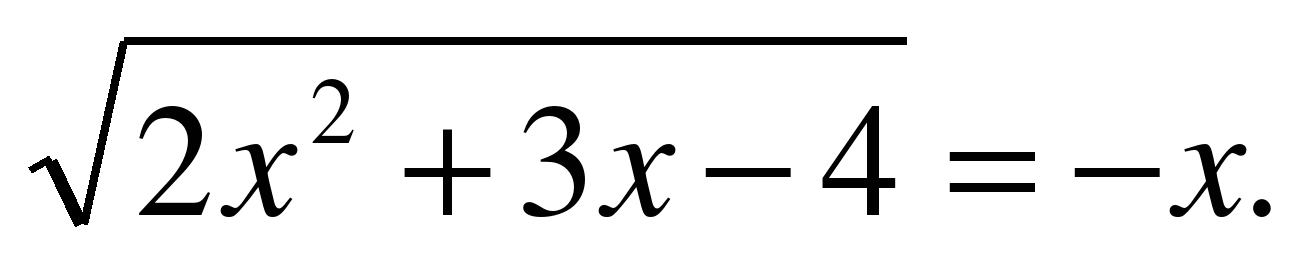
|
|
|
|
|
|
|
B1
B3
B5
B2
ЧАСТЬ 2
B4
|
| Вычислите значение выражения 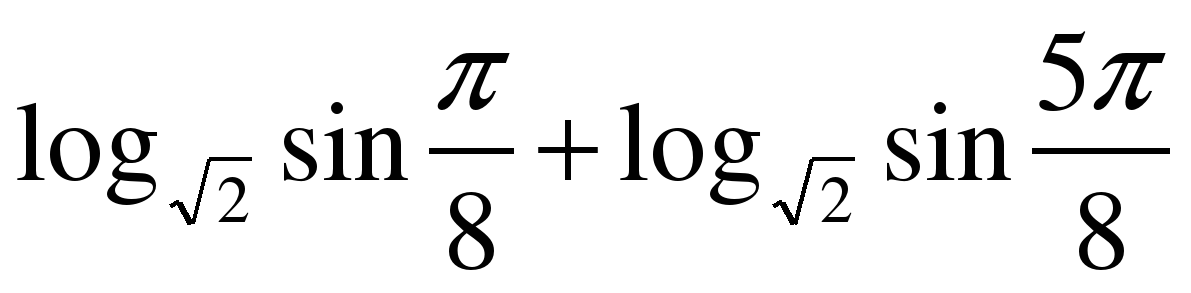 |
|
|
|
|
| Прямая, проходящая через начало координат, касается графика функции 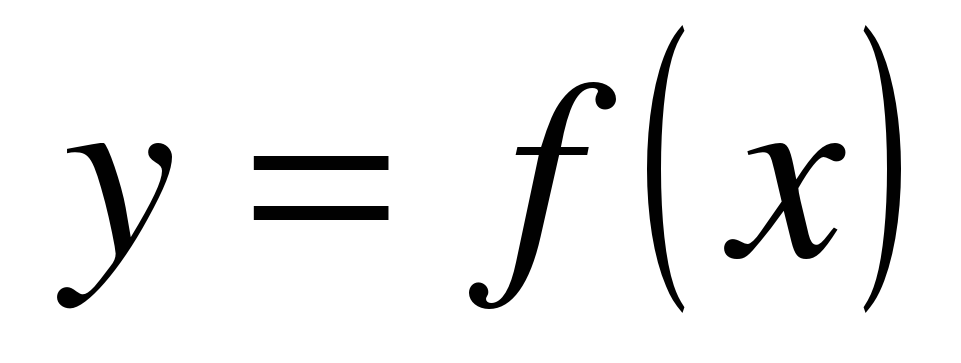 в точке в точке 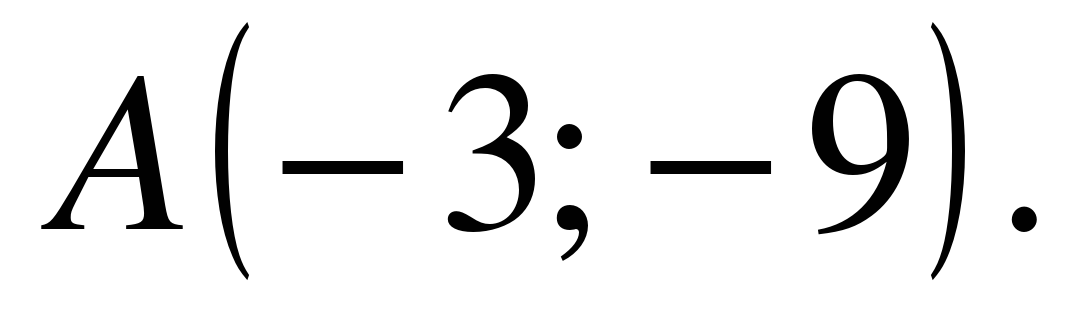 Найдите Найдите 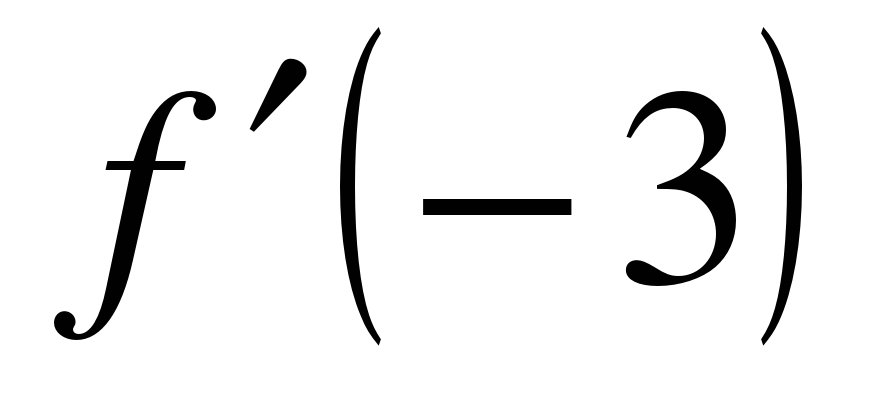 . .
|
|
|
|
|
| Найдите количество целочисленных решений неравенства удовлетворяющих неравенству
|
|
|
|
|
| Решите уравнение
|
|
|
|
|
| Функция 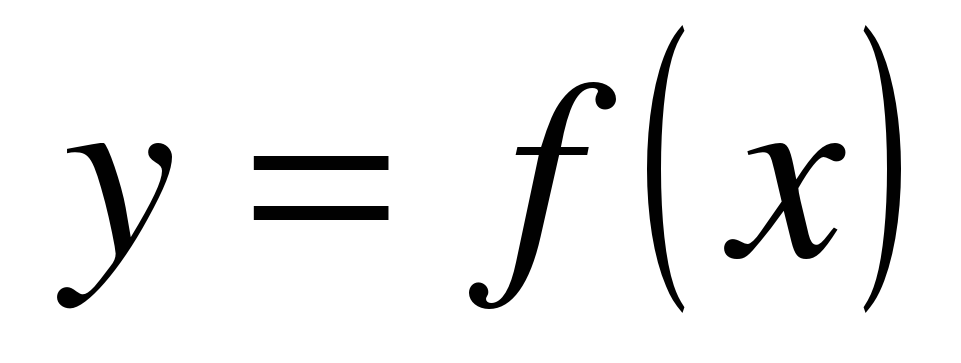 определена на всей числовой прямой и является периодической с периодом 4. На промежутке уравнение имеет ровно 6 различных корней, а на промежутке оно имеет ровно 3 различных корня. Сколько корней имеет уравнение на промежутке ? определена на всей числовой прямой и является периодической с периодом 4. На промежутке уравнение имеет ровно 6 различных корней, а на промежутке оно имеет ровно 3 различных корня. Сколько корней имеет уравнение на промежутке ?
|
|
|
|
*B9
|
| Две картины общей стоимостью 30000 рублей продали на аукционе с прибылью в 40%, причем от продажи одной картины было получено 25% прибыли, а от другой – 50%. Найдите стоимость более дорогой картины.
|
*B10
|
|
|
|
| Высота прямой призмы ABCA1B1C1 равна 18. Основание призмы – треугольник АВС, площадь которого равна 12, АВ = 5. Найдите тангенс угла между плоскостью АВС1 и плоскостью основания призмы. |
B6
B7
B8
*B11
Найдите среднюю линию равнобедренной трапеции, описанной около окружности радиуса 2, если тангенс угла при основании трапеции равен
| Для записи ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем решение. |
|
|
| Найдите точки минимума функции |
|
|
|
|
| Решите уравнение
|
|
| ЧАСТЬ 3
|
|
| | Для записи ответов на задания (С3 – С5) используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем обоснованное решение. |
|
|
|
|
|
| Найдите все значения а, для каждого из которых найдется х из промежутка такое, что значение выражения равно значению выражения |
|
|
|
*C4
|
| Дана сфера диаметром 26. Сечением сферы плоскостью, удаленной от центра сферы на расстояние 5, является окружность с диаметром АВ. Точка D выбрана на сфере, а точка С – на окружности сечения так, что объем пирамиды DABC наибольший. Найдите площадь треугольника DMN, где M и N – середины ребер АС и ВС соответственно.
|
|
|
|
|
| Решите уравнение , если известно, что и
|
C2
C3
C5
C1
8
Просмотр содержимого документа
«Математика_19вариант»
ЕГЭ по МАТЕМАТИКЕ
Вариант № 19
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается
4 часа (240 мин). Работа состоит из трех частей и содержит 26 заданий.
Часть 1 содержит 13 заданий (А1 – А10 и В1 – В3) обязательного уровня по материалу курса «Алгебра и начала анализа» 10-11 классов.
К каждому заданию А1 – А10 приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий надо указать номер верного ответа. К заданиям В1 – В3 надо дать краткий ответ.
Часть 2 содержит 10 более сложных заданий (В4 – В11, С1, С2) по материалу курса «Алгебра и начала анализа» 10-11 классов, а также различных разделов курсов алгебры и геометрии основной и средней школы. К заданиям В4 – В11 надо дать краткий ответ, к заданиям С1 и С2 – записать решение.
Часть 3 содержит 3 самых сложных задания, два – алгебраических
(С3, С5) и одно – геометрическое (С4). При их выполнении надо записать обоснованное решение.
Советуем для экономии времени пропускать задание, которое не удается выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха!
ЧАСТЬ 1
| При выполнении заданий А1 – А10 в бланке ответов № 1 под номером выполняемого задания поставьте знак "´" в клеточке, номер которой соответствует номеру выбранного вами ответа. |
| A1
| . Найдите значение выражения ��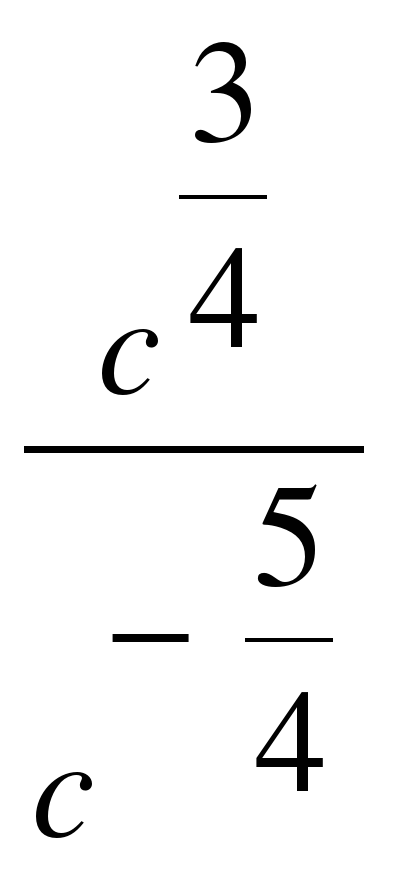 при с = 2 при с = 2 1) 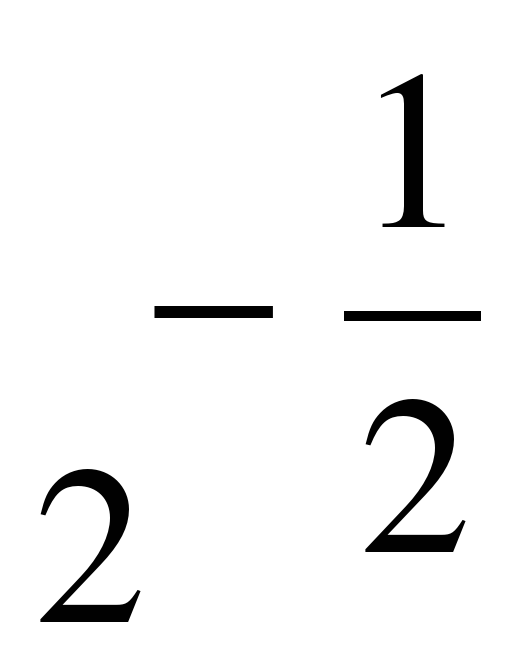 2) 2) 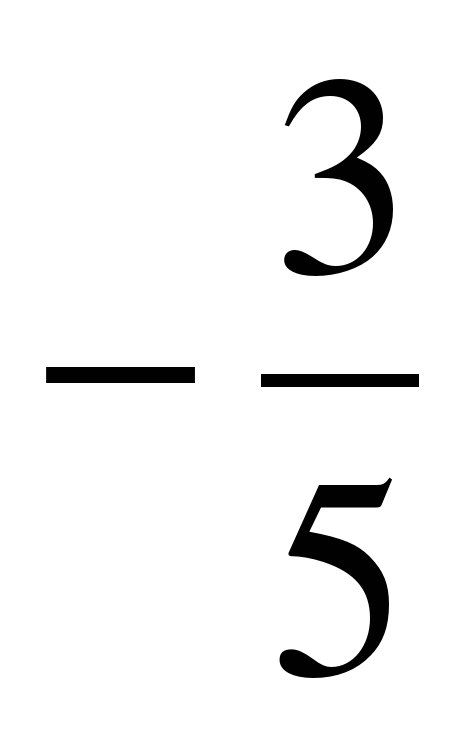 3) �� 3) ��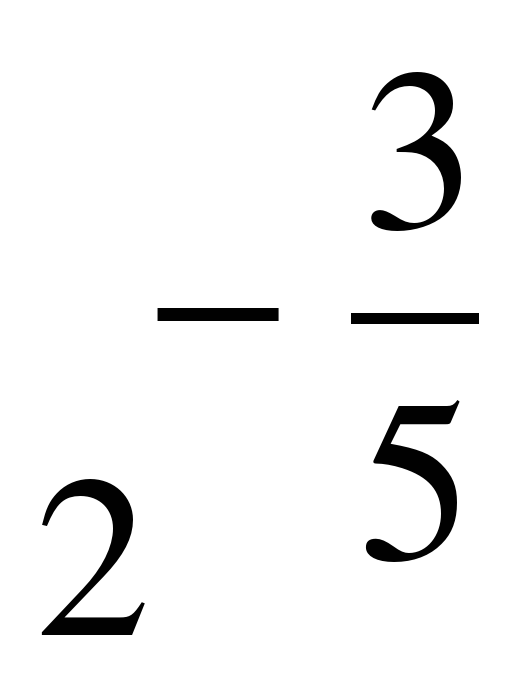 4)�� 4 4)�� 4
|
|
|
|
| A2
| Вычислите: ��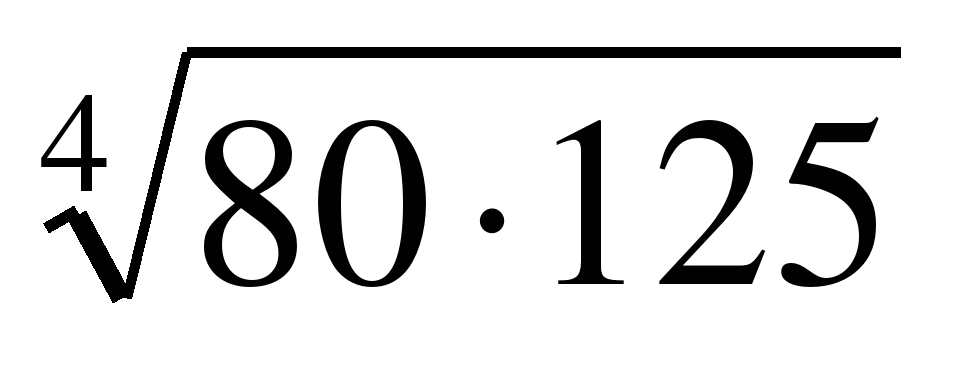 1) 100 2) 10 3) 50 4) 20
|
| A3
| Вычислите: �� 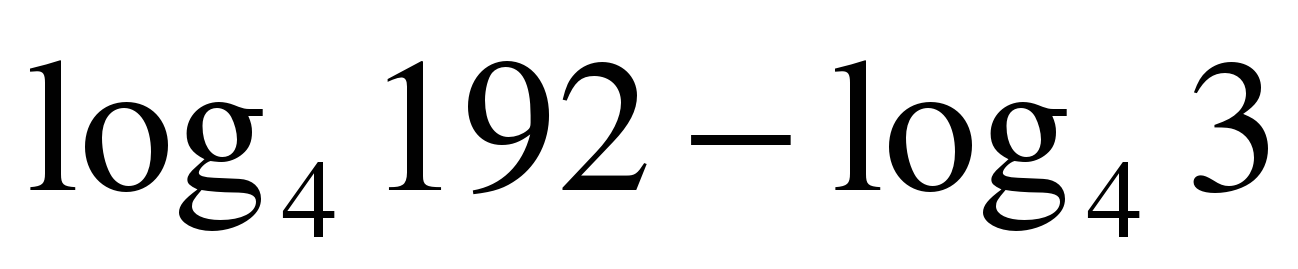 1) 3 2) 64 3) 16 4) ��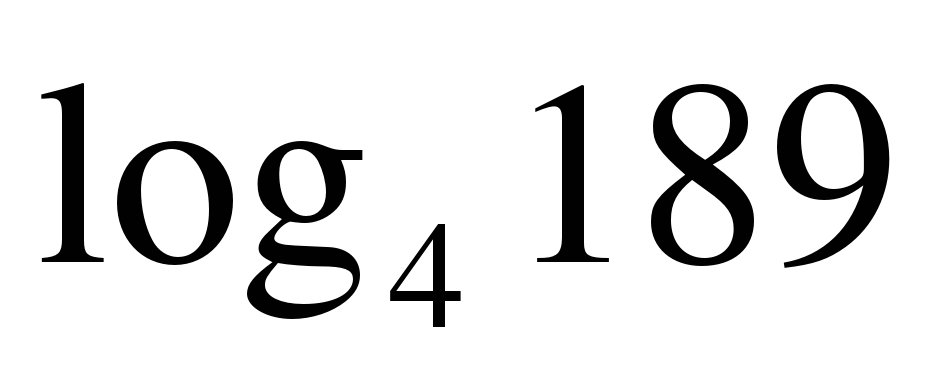
|
| A4
| На каком из следующих рисунков функция, заданная графиком, возрастает на промежутке [0;2] ?
|
| A5
| Найдите производную функции �� 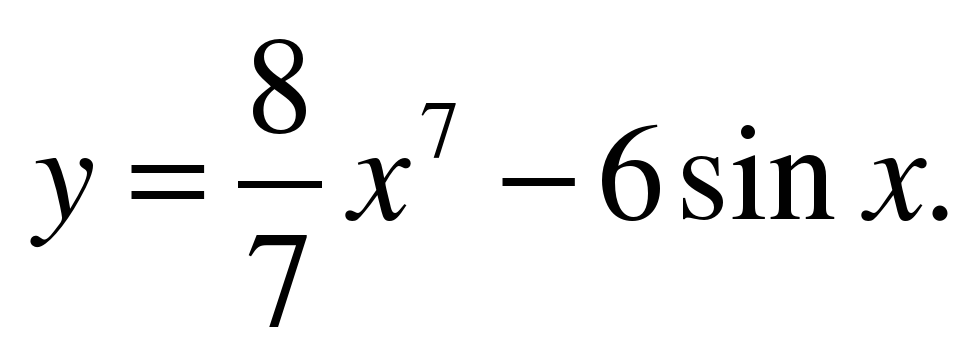 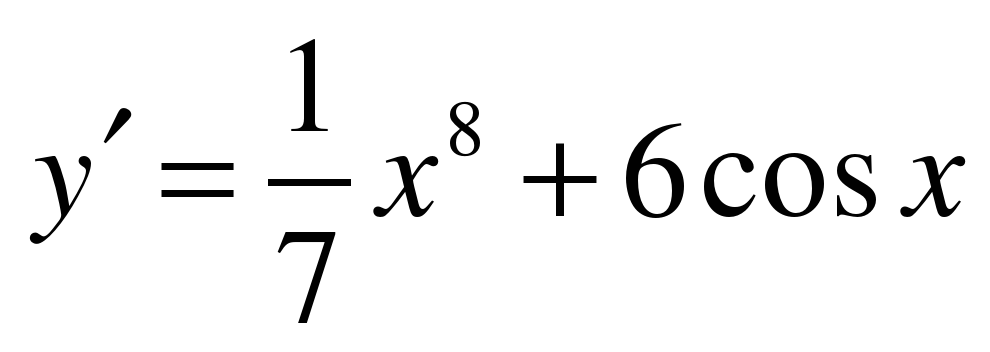 �� 3) �� �� 3) ��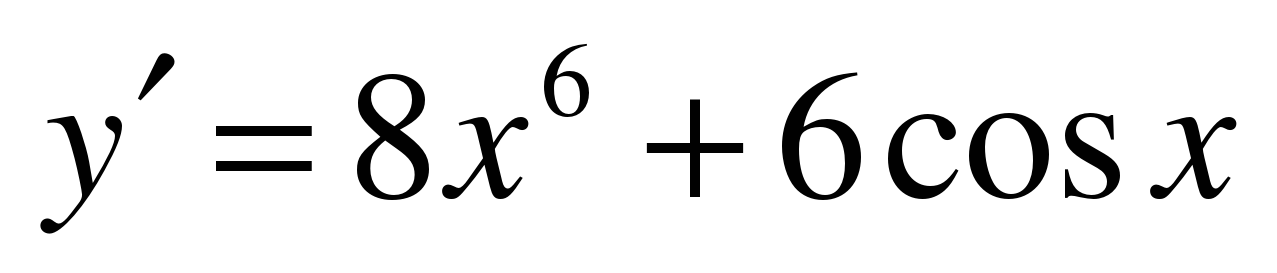  ��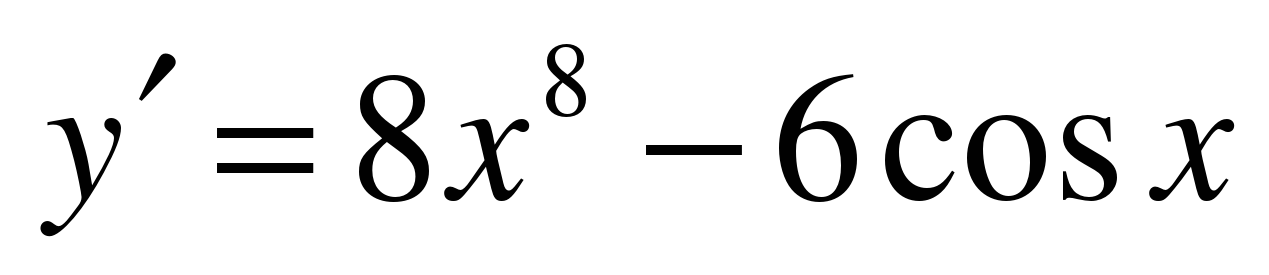 4) 4) 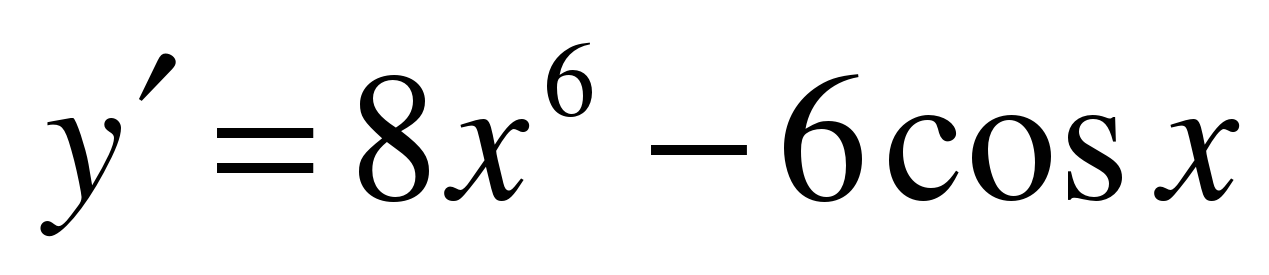 �� ��
|
|
|
|
| A6
| Найдите множество значений функции �� 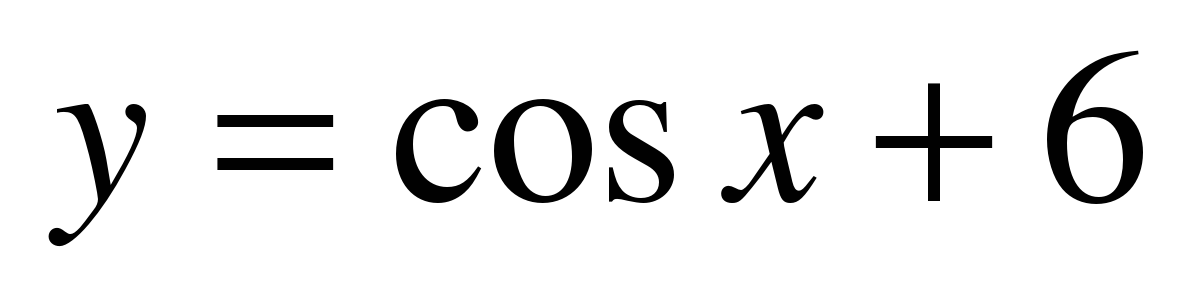 . . 1) 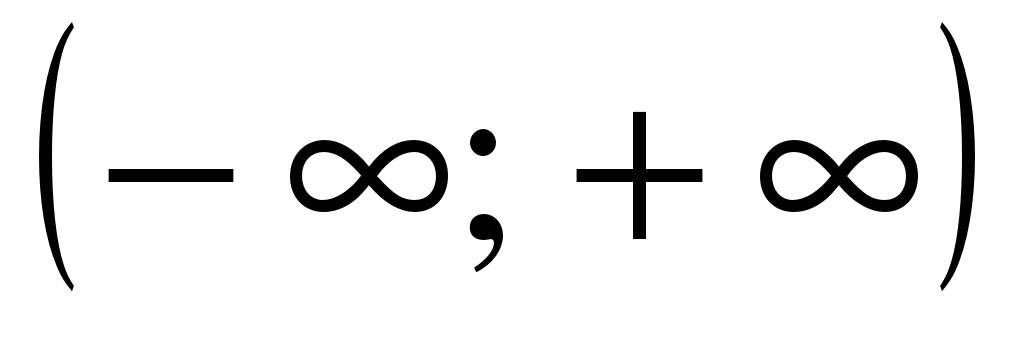 2) [–1; 1] 3) [5; 7]�� 4) [6; 7]. 2) [–1; 1] 3) [5; 7]�� 4) [6; 7].
|
|
|
|
| A7
| | Решите неравенство 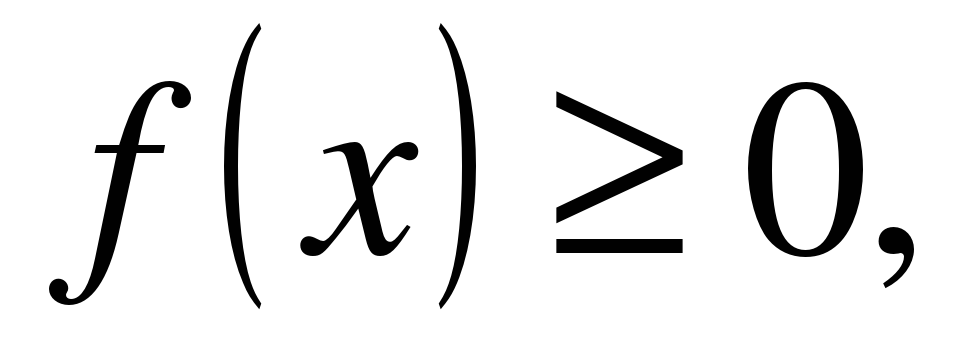 если на рисунке изображен график функции если на рисунке изображен график функции 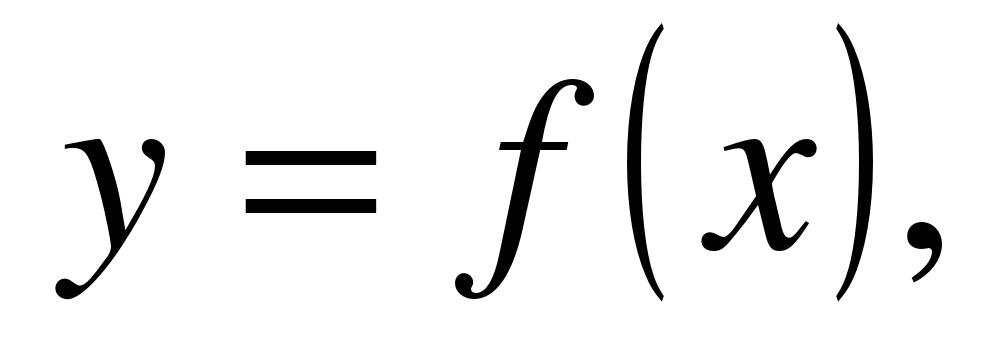 заданной на промежутке заданной на промежутке 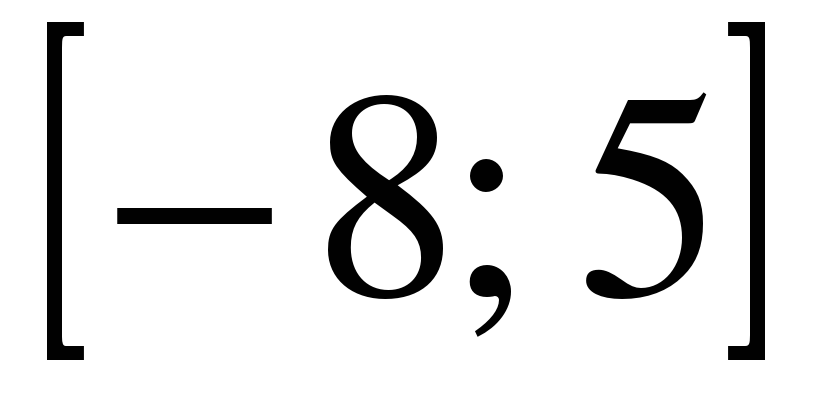 1) 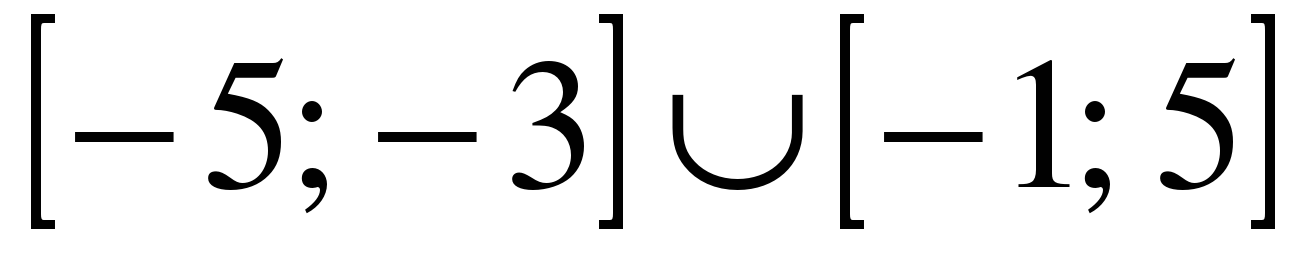 �� �� 2) 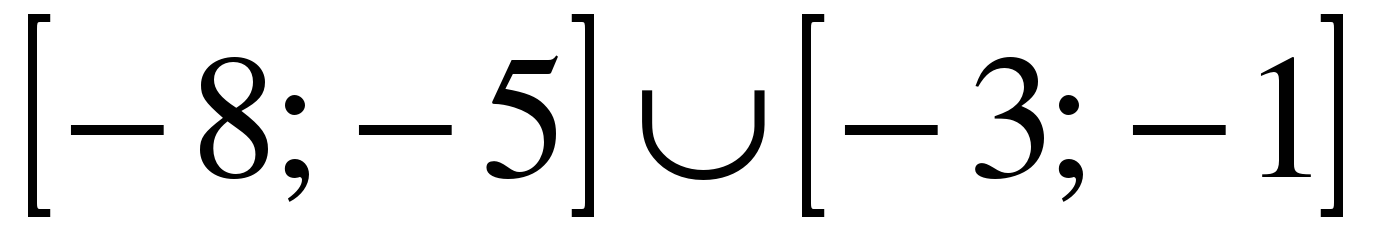 �� �� 3)  4) 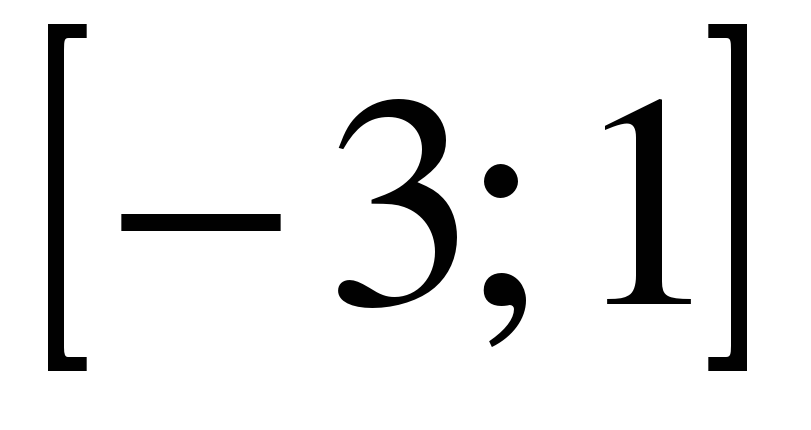 �� ��
| 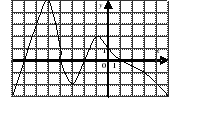 |
|
|
|
|
| A8
| Решите уравнение ��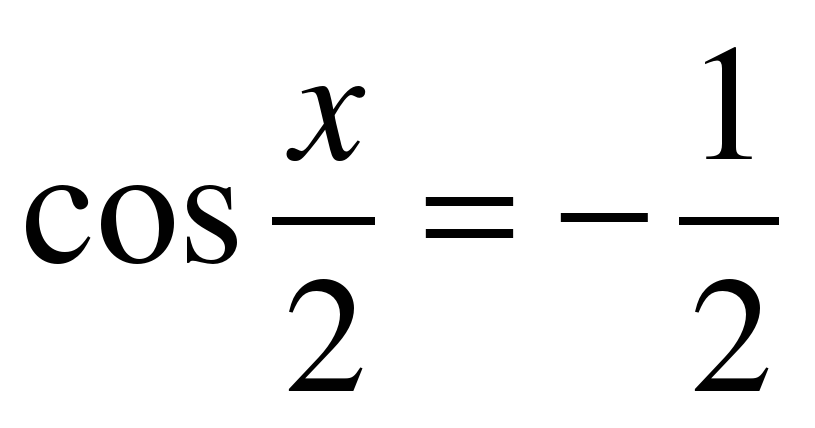 . . 1) 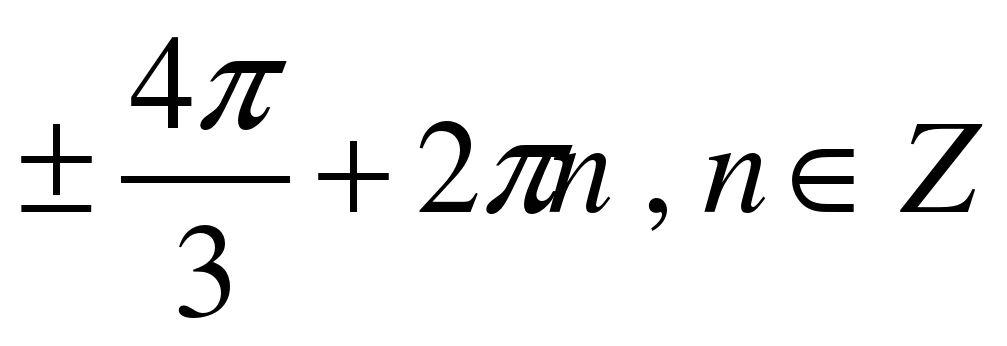 �� �� 2) 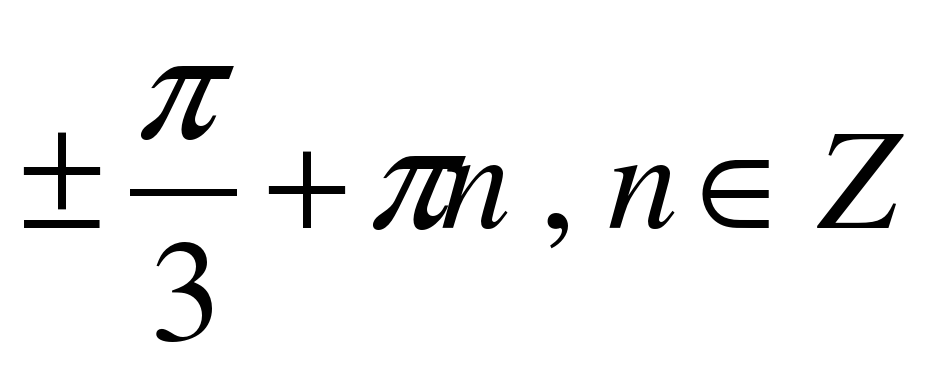 �� �� 3) ��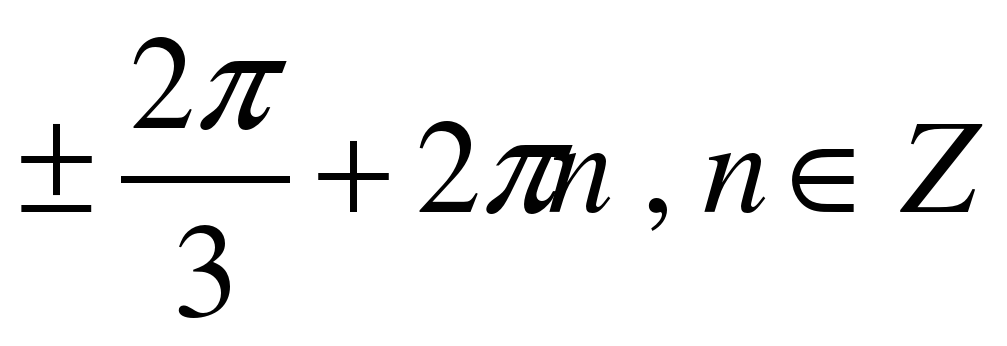 4) 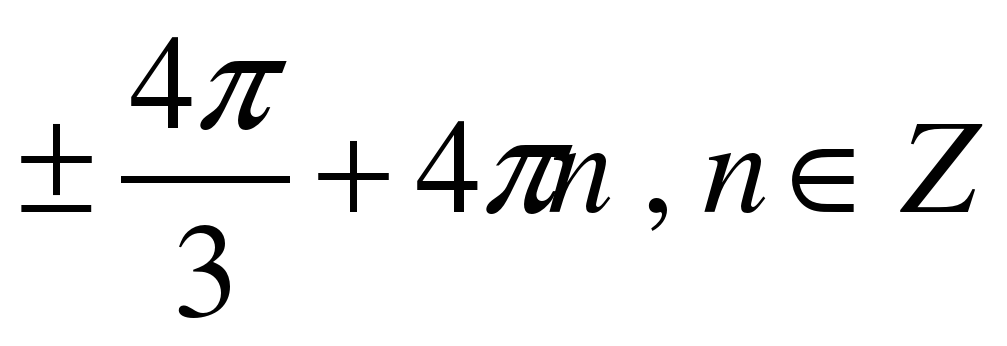 �� �� |
| A9
| Найдите область определения функции �� 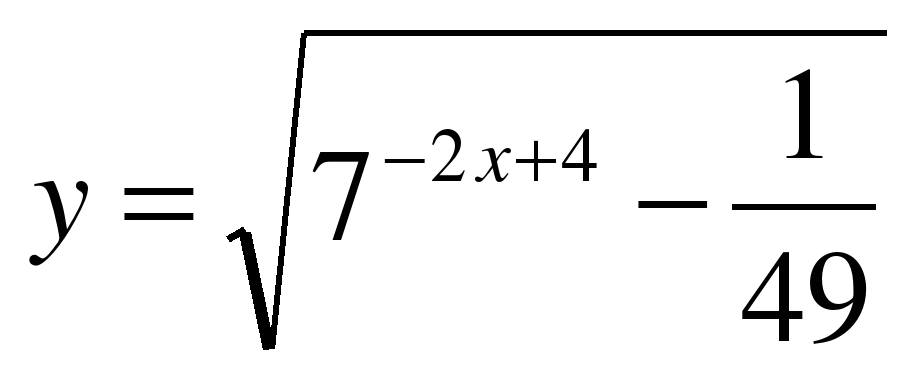 1) 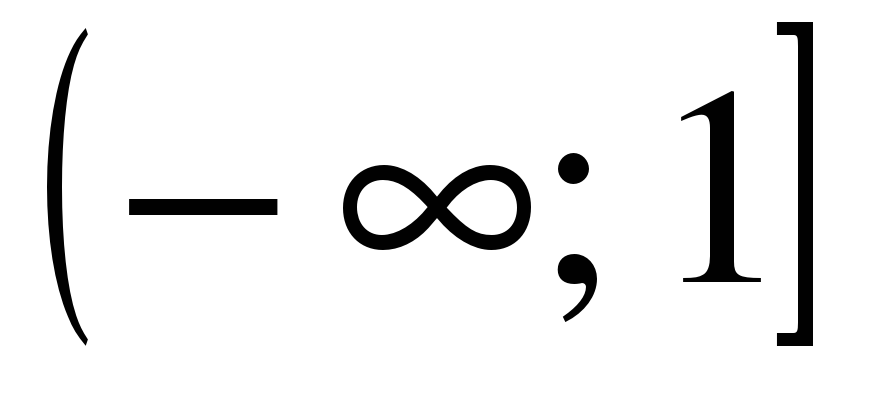 �� 2) �� 2) 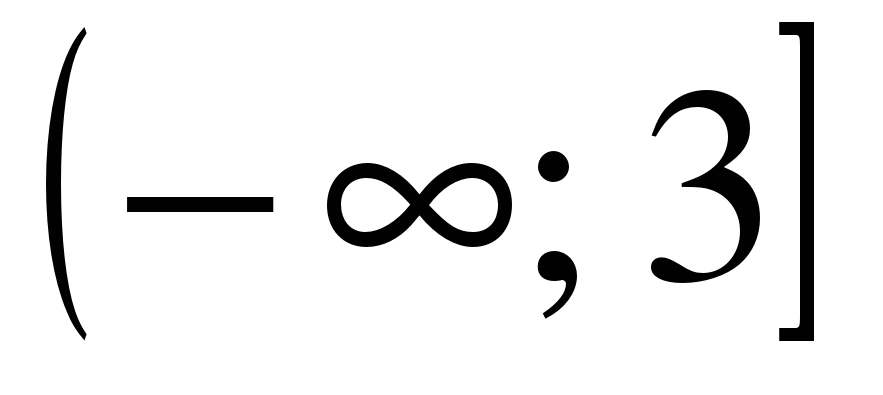 �� 3) �� 3) 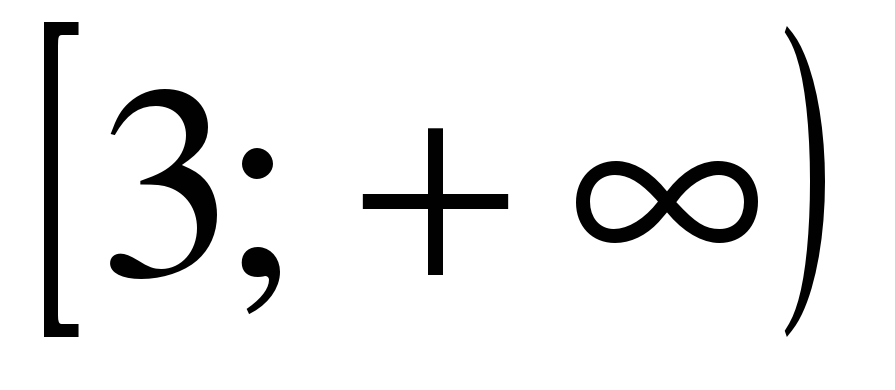 �� 4) �� �� 4) ��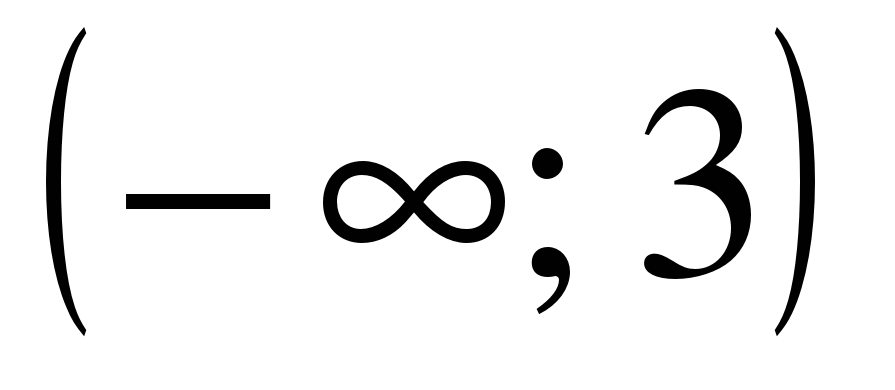
|
|
|
|
|
| Решите неравенство ��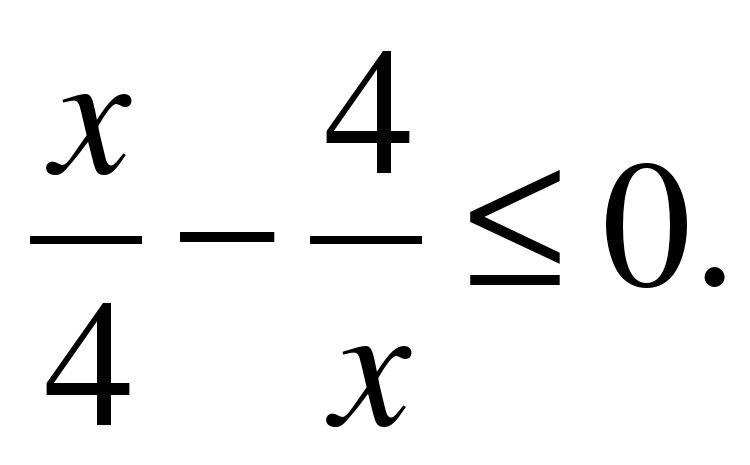 1) ��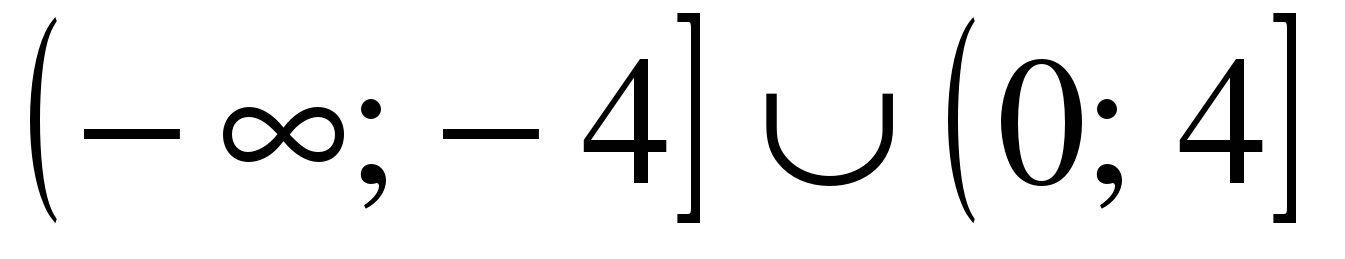 2) 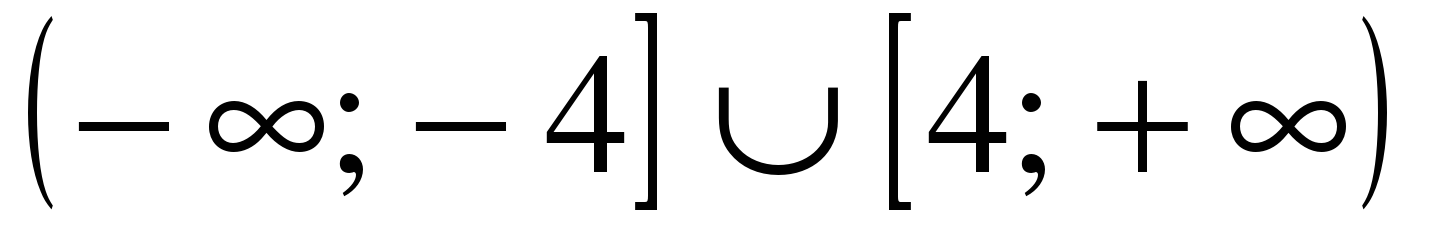 3) 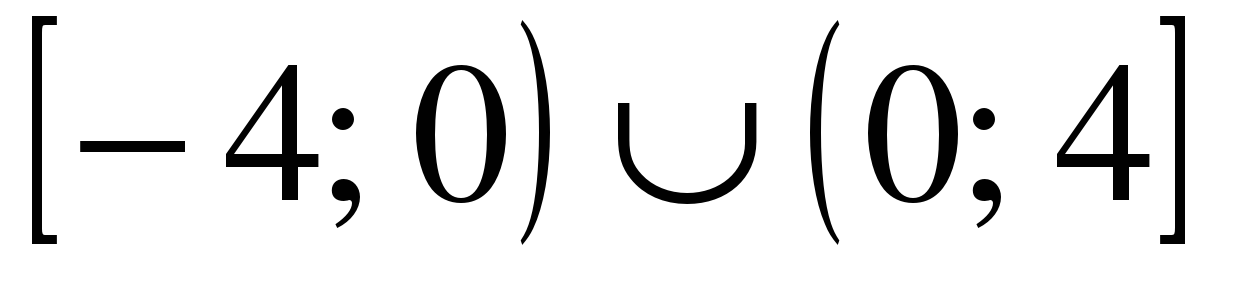 4) ��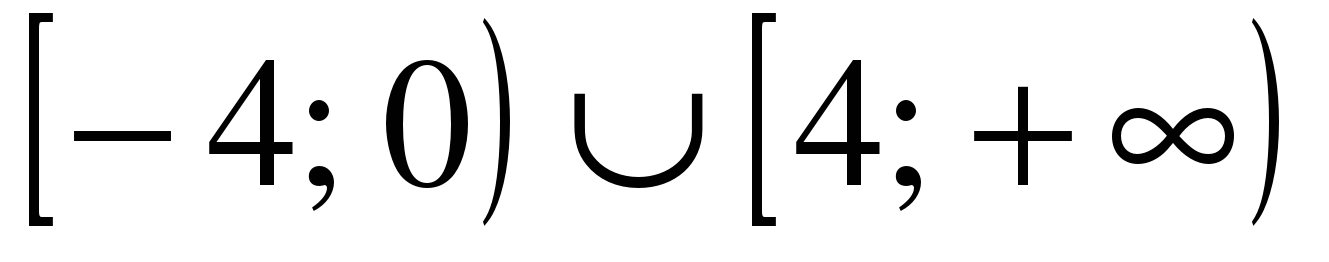 . . |
A10
| Ответом на задания В1 – В11 должно быть некоторое целое число или число, записанное в виде десятичной дроби. Это число надо записать
в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус отрицательного числа
и запятую в записи десятичной дроби пишите в отдельной клеточке в соответствии с приведенными в бланке образцами. Единицы измерений писать не нужно. |
|
| Найдите значение выражения 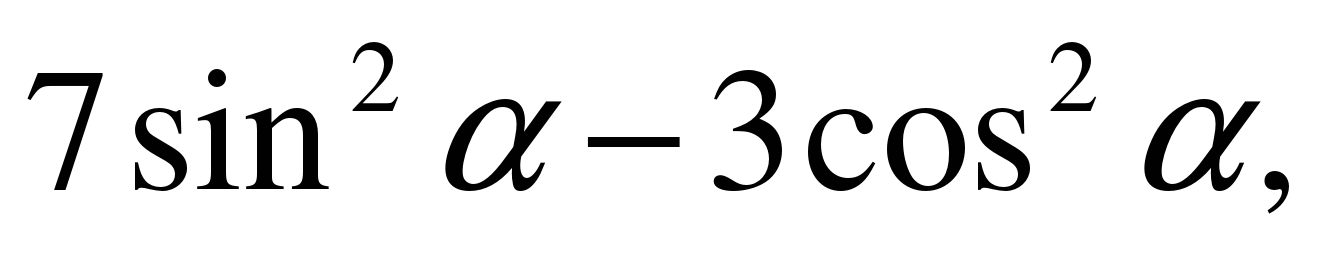 если если 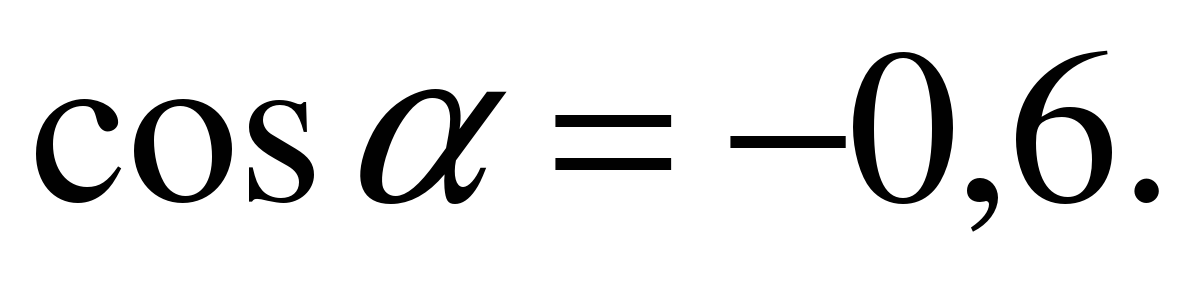
|
|
|
|
|
| Решите уравнение 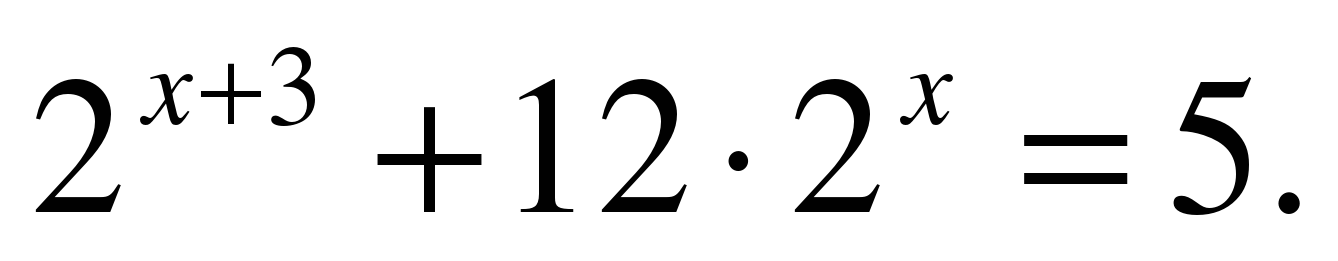
|
|
|
|
|
| Решите уравнение 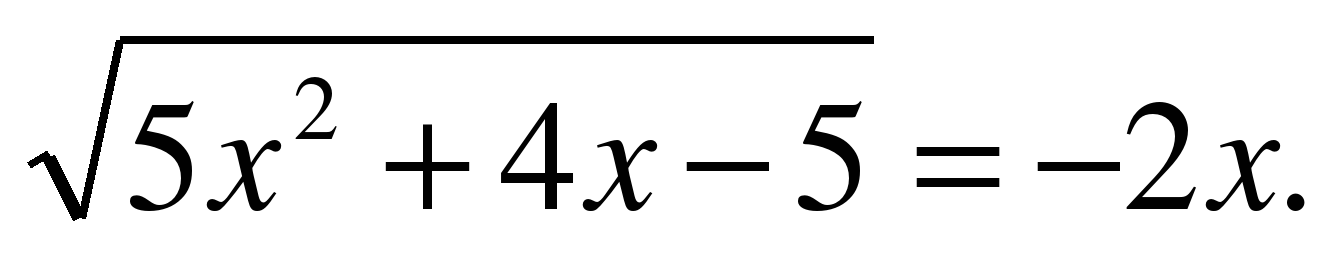 |
|
|
|
|
|
|
B1
B3
B5
B2
ЧАСТЬ 2
B4
|
| Вычислите значение выражения 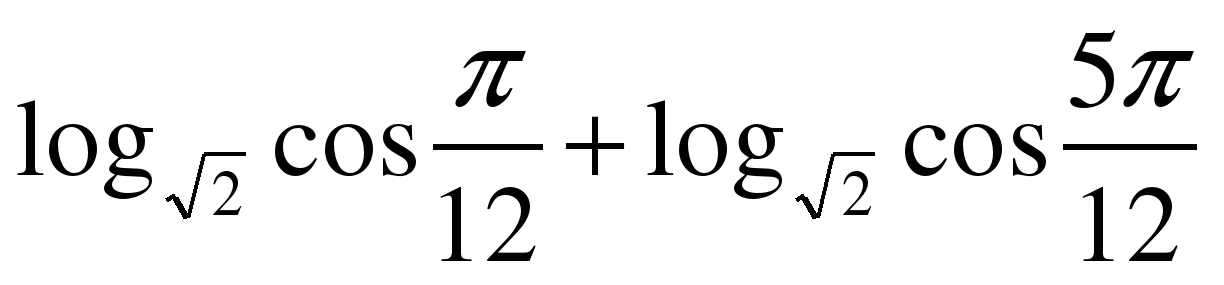 |
|
|
|
|
| Прямая, проходящая через начало координат, касается графика функции 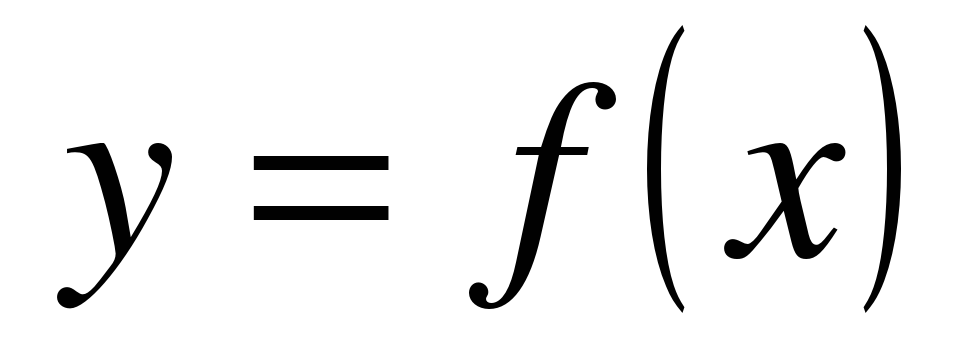 в точке в точке 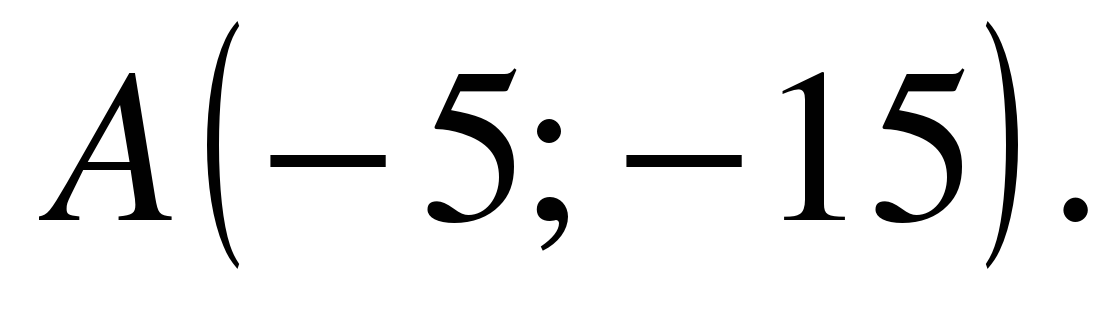 Найдите Найдите 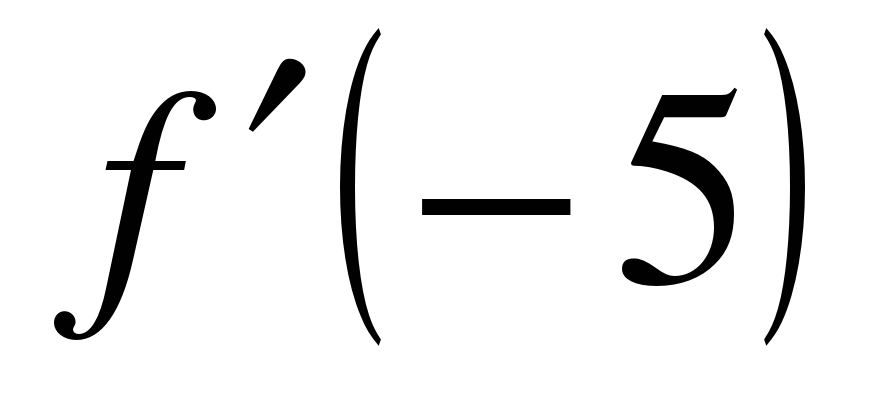 . .
|
|
|
|
|
| Найдите количество целочисленных решений неравенства удовлетворяющих неравенству
|
|
|
|
|
| Решите уравнение
|
|
|
|
|
| Функция 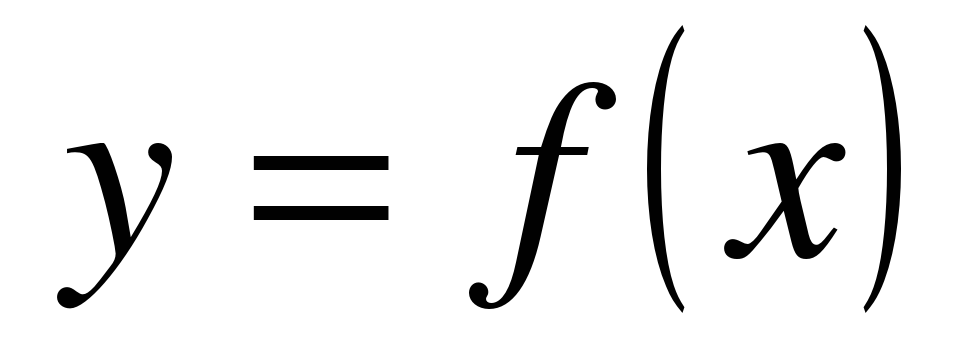 определена на всей числовой прямой и является периодической с периодом 3. Известно, что и Найдите значение выражения определена на всей числовой прямой и является периодической с периодом 3. Известно, что и Найдите значение выражения
|
*B9
|
|
|
|
| На рынке костюм, состоящий из пиджака и брюк, стоит на 20% дешевле, чем такой же костюм в магазине, причем брюки стоят на 35% дешевле, чем в магазине, а пиджак – на 10%. Сколько процентов стоимости этого костюма в магазине составляет стоимость пиджака? |
*B10
Основание прямой призмы ABCDA1B1C1D1 – ромб ABCD с углом 150 и стороной, равной 2. Тангенс угла между плоскостью основания призмы и плоскостью ABC1 равен 4,2. Найдите высоту призмы.
B6
B7
B8
*B11
Найдите радиус окружности, вписанной в равнобедренную трапецию, если средняя линия трапеции равна , а косинус угла при основании трапеции равен
| Для записи ответов на задания С1 и С2 используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем решение. |
|
|
| Найдите точки максимума функции
|
|
|
|
|
| Решите уравнение |
|
| ЧАСТЬ 3
|
|
| | Для записи ответов на задания (С3 – С5) используйте бланк ответов №2. Запишите сначала номер выполняемого задания, а затем обоснованное решение. |
|
|
|
|
|
| Найдите все значения а , для каждого из которых найдется х из промежутка [4; 9) такое, что значение выражения равно значению выражения
|
|
|
|
*C4
|
| Дана сфера диаметром 26. Сечением сферы плоскостью, удаленной от центра сферы на расстояние 5, является окружность с диаметром АВ. Точка D выбрана на сфере, а точка С – на окружности сечения так, что объем пирамиды DABC наибольший. Найдите площадь треугольника DMN, где M и N – середины ребер АС и ВС соответственно.
|
|
|
|
|
| Решите уравнение , если известно, что и |
C2
C3
C5
C1
6