МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«НОВОЦУРУХАЙТУЙСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»
ПРИАРГУНСКОГО РАЙОНА
ЗАБАЙКАЛЬСКОГО КРАЯ
Исследовательская работа на тему:
«Лента Мёбиуса»
Выполнила: ученица 8 «А» класса
МОУ Новоцурухайтуйской СОШ
Симонова Анна Сергеевна
Руководитель: учитель математики
и информатики
Коктышева Юлия Георгиевна
Новоцурухайтуй, 2012 г.
Содержание
Введение ………………………………………………………………………
- История создания листа Мёбиуса…………………………………………
- Изучение свойств ленты Мёбиуса…………………………………………
- Применение ленты Мёбиуса в нашей жизни…………………………….
Заключение…………………………………………………………………….
Список Литературы………………………………………………………………..
Приложения………………………………………………………………………..
Введение
Актуальность исследования. В наше время актуально изучение различных свойств и нестандартных применений необычных фигур. Лист Мёбиуса востребован, его применение развивается, и свойства не до конца изучены. Его ценность состоит в том, что он дал толчок новым обширным математическим исследованиям. Именно поэтому его часто считают символом современной математики и изображают на различных эмблемах и значках, как, например, на значке механико-математического факультета Московского университета (см. Приложение 1). Актуальность данной тематики предопределило выбор темы научного исследования.
Цель исследования: исследование поверхности ленты Мебиуса.
Гипотеза: если мы исследуем поверхность ленты Мебиуса, то определим её практическое применение
Объект исследования: лента Мебиуса.
Предмет исследования: свойства ленты Мёбиуса.
Задачи:
- познакомиться с историей появления ленты Мебиуса;
- выявить и исследовать свойства ленты Мебиуса;
- установить области применения ленты Мебиуса.
Методы исследования: анализ литературы по данной теме; сравнение; обобщение; моделирование (метод моделирования позволил мне получить информацию о различных свойствах изучаемого объекта на основе опытов с его материальными моделями).
- История создания листа Мёбиуса
Таинственный и знаменитый лист Мебиуса (иногда говорят: "лента Мёбиуса") придумал Август Фердинанд Мёбиус (1790–1868), ученик "короля математиков" Гаусса, немецкий геометр Лейпцигского университета. Первоначально Мёбиус был астрономом. Он ввел аналитические методы исследования, установил понятие проективного преобразования и существование односторонних поверхностей. В возрасте 68 лет ему удалось сделать открытие поразительной красоты. Это открытие односторонних поверхностей, одна из которых – лист Мёбиуса.
В 26 лет Мёбиус стал профессором, руководителем астрономической лаборатории в Лейпцигском университете. Научные статьи, лекции, работа. Все как у обычного профессора университета. Рассеянного доброго чудака студенты боготворили.
Как –то раз в доме на пороге комнаты появилась любимая жена. Правда, она была не в хорошем расположении духа. Правильнее сказать, она была разгневана, что для мирного дома Мебиусов было почти так же невероятно, как три раза в год увидеть парад планет, и категорически требовала немедленно уволить служанку, которая настолько бездарна, что даже не способна правильно сшить ленту.
Хмуро разглядывая злосчастную ленту, профессор воскликнул: “Ай да, Марта! Девочка не так уж глупа. Ведь это же односторонняя кольцевая поверхность. У ленточки нет изнанки!” Идея пришла ему в голову, когда служанка неправильно сшила ленту.
Открытая поверхность получила математическое обоснование и имя в честь описавшего ее математика и астронома.
Лента вдохновила на подвиги ни одного добряка-профессора. Взял ее на вооружение и цех парижских портных. Отныне в качестве экзамена для новичка, претендовавшего на зачисление в цех, было пришивание к подолу юбки тесьмы в форме ленты Мебиуса.
Лист Мёбиуса – это топологический объект, простейшая односторонняя поверхность с краем. Сама топология началась именно с листа Мёбиуса.
Слово это придумал Иоганн Бенедикт Листинг, который почти в тоже время, что и его коллега, предложил в качестве первого примера односторонней поверхности уже знакомую нам перекрученную ленту.
Топология (от греч. το?πος — место) — часть геометрии, изучающая в самом общем виде явление непрерывности, а также свойства обобщенных геометрических объектов. Топология является одним из самых «молодых» разделов современной геометрии, в котором изучаются свойства таких фигур, которые не меняются, если их гнуть, растягивать, сжимать, но не склеивать и не рвать, т. е не изменяются при деформациях. Примером топологических объектов являются: буквы И и Н, тонкие длинные воздушные шарики.
- Изучение свойств ленты Мёбиуса
Изготовление ленты Мёбиуса. Для изготовления ленты Мёбиуса потребуются бумажные полосы длиной 30 см и шириной 3 см.
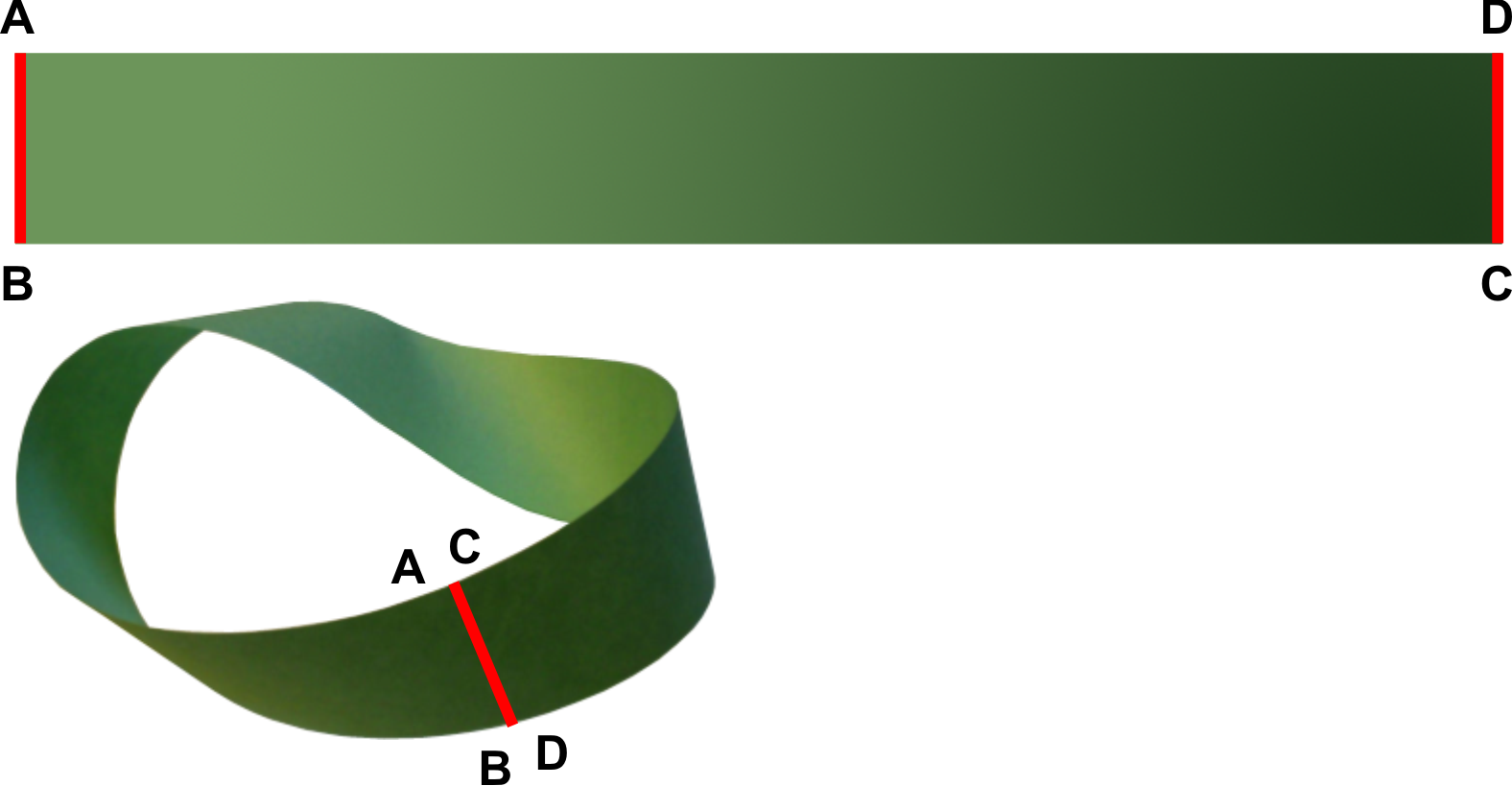
Возьмем бумажную ленту АВСD, разделенную по ширине пополам пунктирной линией. Прикладываем ее концы АВ и СD друг к другу и склеиваем так, чтобы точка А совпала с точкой C, а точка B с точкой D. Получилось знаменитое в математике бумажное кольцо, которое получило особое название - "Лента Мёбиуса".
Опыты с лентой Мёбиуса
1 опыт. Поставьте точку на одной стороне ленты и начертите линию вдоль неё.
Результат: линия проходит непрерывно по двум сторонам, заканчиваясь в начальной поставленной точке.
2 опыт. Попробуйте закрасить ленту Мёбиуса, а затем обычное кольцо.
Результат: лист Мёбиуса закрасился полностью, а вот у кольца одна сторона закрашена, а другая – нет.
3 опыт. Изготовим из бумаги паука и муху, и отправим их «гулять» сначала по обычному листу, а затем по листу Мёбиуса при этом не пересекая края кольца и ленты.
Результат: на обычном кольце паук и муха никогда не встретятся, не пересекая края. На листе Мёбиуса паук и муха встретятся не пересекая края в любом случае.
4 опыт: разрежем кольца пополам вдоль. (Чтобы проверить, какая поверхность получилась необходимо снова прочертить непрерывную линию.)
Результат: получилось два кольца, причем длина окружности каждого будет такой же, как длина окружности первоначально взятого. У листа Мёбиуса получилось одно большое кольцо перекрученное в два раза (в виде восьмерки).
5 опыт: разрежем кольцо вдоль, отступив от края 1/3. (Чтобы проверить, какая поверхность получилась необходимо снова прочертить непрерывную линию.). Точно также разрежем и лист Мёбиуса.
Результат: получилось 2 кольца одно уже, другое шире. В листе Мёбиуса получилось два сцепленных друг с другом кольца, одно маленькое – другое большое.
На основе проведенных опытов можно сделать вывод:
- Лента Мёбиуса имеет только один край.
- Имеет только одну поверхность.
- Объекты по поверхности ленты будут двигаться бесконечно
- Лист Мёбиуса - топологический объект. Как и любая топологическая фигура, лента Мёбиуса не меняет своих свойств, пока ее не разрезают, не разрывают.
- Применение ленты Мёбиуса в нашей жизни
Лента Мёбиуса получила своё применение во многих областях нашей жизни.
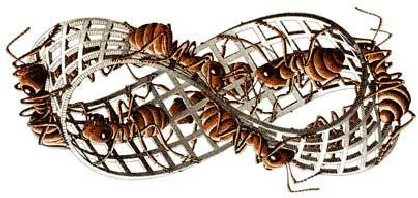
Лист Мёбиуса служил вдохновением для скульптур и для графического искусства. Одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту, был Морис Корнелис Эшер. Одна из известных – муравьи, ползающие по поверхности Ленты Мёбиуса. (см. Приложение 2)
Кроме того, Лист Мёбиуса встречается и в картинах других художников. (см. Приложение 3)
Встречается он и в архитектуре. (см. Приложение 4) Так, например проектирование национальной библиотеки в Астане по названием «Юрта Мёбиуса».
Их дизайн основан на сочетании четырех форм: кольца, ротонды, арки и юрты, при этом объединенных по принципу ленты Мёбиуса.
Так же есть парковая скамья, повторяющая очертания ленты Мебиуса, ротонда для любования пейзажем посреди поля и дом-гнездо на воде вошли в шорт-лист общероссийской премии в области деревянной архитектуры АРХИWOOD.
Поразил нас и Поп-арт, разработанный для вьетнамского города Хошимин. Со стороны, кажется, что этот многофункциональный комплекс похож на американские горки. Хотя основой для внешнего вида Everrich стали вовсе не американские горки, а лента Мебиуса.
Общая площадь этого многофункционального комплекса составит почти 632 тысячи квадратных метров, 37 этажей. На них расположатся 3 100 жилых квартир, офисные и гостиничные помещения, торговые залы и развлекательный центр.