СЦЕНАРИЙ
МАРУШКО.
«Красота привлекает, исследование увлекает»
ГОРСКАЯ.
Математика,
если на нее правильно посмотреть,
отражает не только истину,
но и несравненную красоту.
Бертран Рассел
ГОРСКАЯ. Когда-то большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, коническое сечение, многоугольник, сфера, квадратичная поверхность, а также их комбинациями. К примеру, что может быть красивее утверждения о том, что планеты в нашей солнечной системе движутся вокруг солнца по эллиптическим орбитам?
МАРУШКО. Однако многие природные системы настолько сложны и нерегулярны, что использование только знакомых объектов классической геометрии для их моделирования представляется безнадежным. Как, к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать то многообразие биологических конфигураций, которое мы наблюдаем в мире растений и животных? Представьте себе всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела. Представьте, как хитроумно устроены легкие и почки, напоминающие по структуре деревья с ветвистой кроной. Столь же сложной и нерегулярной может быть и динамика реальных природных систем. Как подступиться к моделированию каскадных водопадов или турбулентных процессов, определяющих погоду? Все эти сложные вопросы легко решить с помощью фракталов.
ГОРСКАЯ. Фракталы можно встретить везде. Это самые разные системы, начиная от кристаллов и просто кластеров (различного рода скоплений, таких как облака, реки, горы, материки, звёзды), заканчивая экосистемами и биологическими объектами (от листа папоротника до человеческого мозга). Нередко то, что мы наблюдаем в природе, интригует нас бесконечным повторением одного и того же узора, увеличенного или уменьшенного во сколько угодно раз. Вы смотрели в «замороженное» окно? Какие красивейшие узоры можно увидеть! Например, у дерева есть ветви. На этих ветвях есть ветки поменьше и т.д. Теоретически, элемент «разветвление» повторяется бесконечно много раз, становясь с каждым разом все меньше и меньше. То же самое можно заметить, разглядывая фотографию горного рельефа. Попробуйте немного приблизить изображение горной гряды - вы снова увидите горы. Так проявляется характерное для фракталов свойство самоподобия.
МАРУШКО Целью нашего проекта является исследование структуры фракталов и формулы фрактальной размерности, использование данной формулы при вычислении размерности других геометрических конфигураций, найти применение фрактальных фигур в национальном искусстве.
ГОРСКАЯ Гипотеза заключается в программировании новой фрактальной фигуры, которую можно использовать в национальном искусстве, вычислении ее фрактальной размерности.
МАРУШКО .
Перед нами сегодня стоят Задачи:
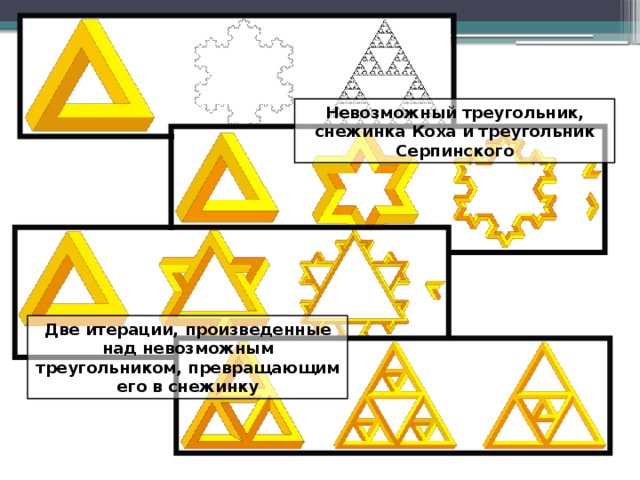
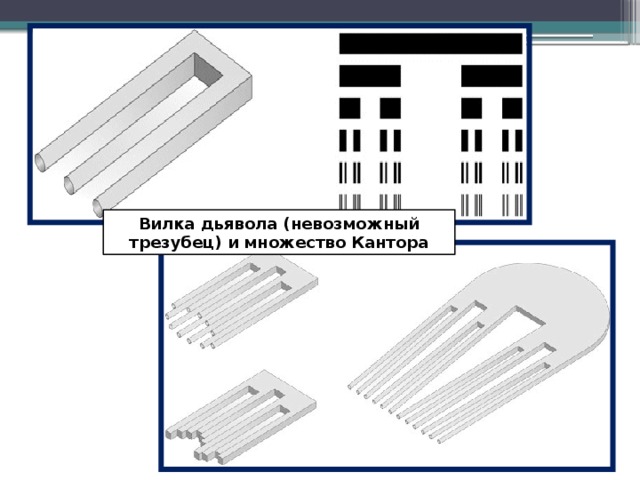
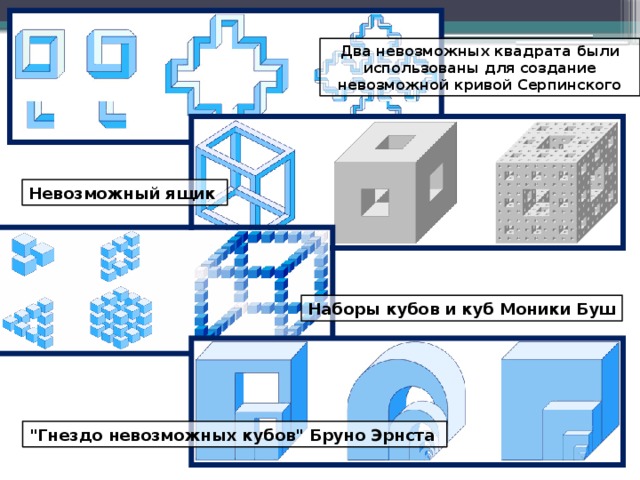
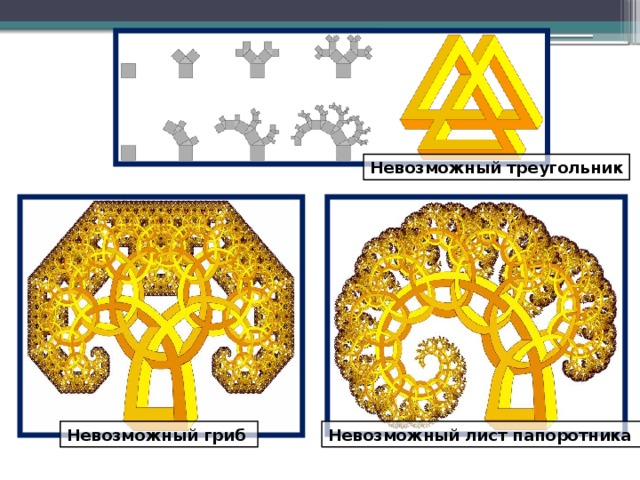
СЛАЙДЫ –МОТИВАЦИЯ «НЕВОЗМОЖНОЕ ВОЗМОЖНО?»
ГОРСКАЯ
СЛАЙД. Чем же актуальны фракталы?
ВЫСТУПЛЕНИЕ СТУДЕНТОВ «ФРАКТАЛЫ»
МАША.
Бенуа Мандельброт стал создателем новой геометрии. Первым из его великих озарений было открытие того факта, что необычные, почти патологические, структуры, которые долго игнорировались учёными, являются универсальны¬ми... Фракталы, которые он, таким образом, открыл и снабдил общей теорией, представлены почти повсеместно в природе. Он от¬крыл дотоле неизвестный мир – поэтому ему потребовалось понятие, объединяющее новый класс явлений. «Однажды зимним днём 1975 года Мандельброт работал над своей пер¬вой монографией... Он понял, что должен найти некий термин, который стал бы стержнем новой геометрии. Одолжив у сына латинский словарь, он стал перелистывать его и наткнулся на слово fractus, образованное от глагола fragere – “разбивать”. Слово было созвучно английским fracture (разрыв) и fraction (дробь). Так Мандельброт придумал термин fractal, который вошёл как существительное и прилагательное в современные английский и французский языки».
Официальное рождение фрактальной геометрии состоялось в 1982 году после выхо¬да в свет книги Бенуа Мандельброта «Фрактальная геометрия природы».
Что же такое фрактал? Исследователи до сих пор не могут при¬йти к единому определению этого феномена. Но человек, один раз увидевший фрактал, узнает его в любых формах, какие бы он не принимал. Можно сказать, что в самом понятии фрактала большая роль отведена интуитивному пониманию.
И, тем не менее ЧТО ЖЕ ТАКОЕ ФРАКТАЛЫ?
ЛИЛЯ.
1. Фракталы - множества точек в пространстве, обладающие свойством самоподобия: некоторые их части являются точными уменьшенными копиями целого. Это новое направление в математике, совершившее в научной парадигме переворот, сравнимый по значимости с теорией относительности и квантовой механикой. Объекты фрактальной геометрии по своему внешнему виду резко отличаются от привычных для нас 'правильных' геометрических фигур. Фактически, это прорыв в математическом описании систем, которые на протяжении долгого времени такому описанию не поддавались. Фрактальные множества обладают рядом необычных характеристик.
Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:
¬- обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.
- является самоподобной или приближённо самоподобной.
- обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
Многие объекты в природеобладают фрактальными свойствами, например, побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.
Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.
Для того чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации. Фракталы делятся на три большие группы: алгебраические фракталы, геометрические и стохастические фракталы. Но также каждая группа фракталов имеет свои собственные типы фракталов, которых очень много и которые все очень разные. Группы отличаются между собой по строению.
Для полного понимания каждой группы фракталов рассмотрим каждую группу отдельно с примером.
2.Для того чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации. Фракталы делятся на три большие группы: алгебраические фракталы, геометрические и стохастические фракталы. Но также каждая группа фракталов имеет свои собственные типы фракталов, которых очень много и которые все очень разные. Группы отличаются между собой по строению.
Для полного понимания каждой группы фракталов рассмотрим каждую группу отдельно с примером.
БРЫЛЕВА НАСТЯ.
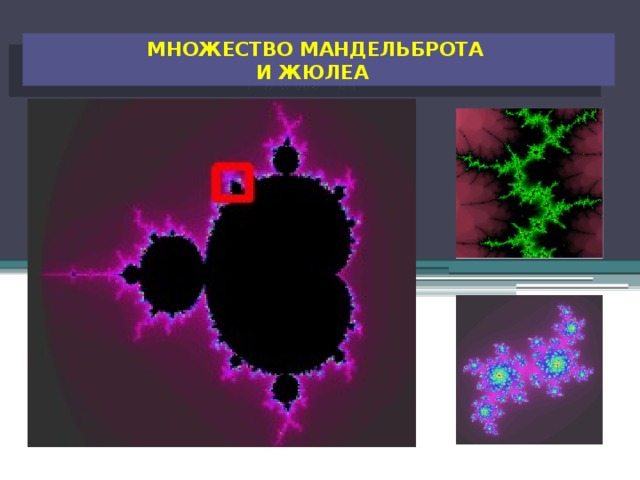
Множества Мандельброта и Жюлиа.
В 1918 г. 25-летний француз Гастон Жюлиа (1893-1978) залечивал свои раны в госпитале. Изнывая от безделья, молодой Жюлиа заинтересовался поведением точки последовательности на комплексной плоскости. Гастон пришёл к выводу, что последовательность точек может вести себя по-разному. Точка последовательности может уходить в бесконечность либо может стремиться к некоторой конечной точке комплексной плоскости, называемой аттрактором. То есть аттрактор это точка притяжения итерационного процесса или предел последовательности. Множество всех точек плоскости с конечными аттракторами называется множеством Жюлиа.
На СЛАЙДЕ изображено множество Жюлиа , КОТОРОЕ превращается в причудливую ломаную линию ИЛИ В сказочный ковёр .
При некоторых значениях множество Жюлиа теряет связность и рассыпается на множество мелких осколков. Такие множества Жюлиа называются пылью Фату.
Множеством Мандельброта называется множество всех точек , при которых множество Жюлиа связно.
В его основе лежит кардиоида с вершинами на вещественной Множество Мандельброта облеплено почками, наростами и причудливыми усами. Эти почки и наросты в свою очередь облеплены более мелкими почками и так далее.
При более сильном увеличении в окрестностях границ множества Мандельброта обнаруживаются уменьшенные копии самого множества Мандельброта.
Андриен Дуади и Дж. Хаббард доказали, что множество Мандельброта связно.
МАШИРОВА ДАРИНА.
Бассе́йны Нью́тона,— ЭТО разновидность алгебраических фракталов.
Этот вопрос заинтересовал Артура Кэли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.
Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
ГЛИНСКАЯ ВИКА.
ТРЕУГОЛЬНИК СЕРПИНСКОГО
В 1915 году польский математик Вацлав Серпинский придумал занимательный объект, известный как решето Серпинского. Этот треугольник один из самых ранних известных примеров фракталов. Существует несколько способов построения этого фрактала. Один из них представляет следующий процесс. Берётся сплошной равносторонний треугольник, на первом шаге из центра удаляется перевёрнутый треугольник. На втором шаге удаляется три перевёрнутых треугольника из трёх оставшихся треугольников. Продолжая этот процесс, на ЭННОМ шаге удаляем ТРИ перевёрнутых треугольникА из центров ТРЕХ оставшихся треугольников. Конца этому процессу не будет, и в треугольнике не останется живого места, но и на части он не распадётся - получится объект состоящий из одних только дырок. Это и есть треугольник Серпинского. Треугольник Серпинского также называют салфеткой Серпинского.
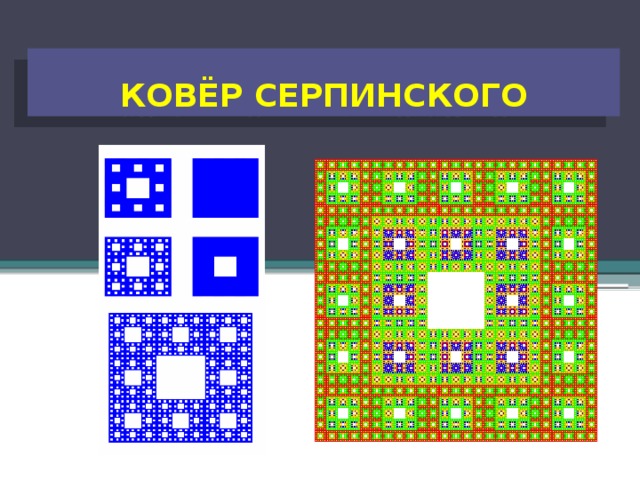
Ковёр Серпинского
Аналогично салфетке Серпинского можно строить ковер Серпинского , который является двуxмерным аналогом канторовского множества исключенных средних третей. Строится ковер Серпинского следующим образом. Вначале берётся квадрат со стороной равной единице, затем каждая сторона квадрата делится на три равные части, а весь квадрат, соответственно, на девять одинаковых квадратиков со стороной равной . Из полученной фигуры вырезается центральный квадрат. Затем такой же процедуре подвергается каждый из 8 оставшихся квадратиков и т. д.
Губка Менгера
Рецепт создания пространственного аналога квадратного ковра Сер-пинского, называемого губкой Менгера , состоит в следующем. Каждая грань куба, имеющая единичную длину, делится на 9 равных квадратиков так же, как и при построении квадратного ковра Серпинского. В результате исходный куб разбивается на 27 одинаковых кубиков с длиной ребра, равной 1/3. Затем, удаляя 7 кубиков (один центральный и 6 из центра каждой из граней), проти¬воположные грани исходного куба соединяются сквозным централь¬ным отверстием квадратной формы. В результате из 27 остается 20 маленьких кубиков.
Такая процедура с вырезанием сквозных отверстий и последующего превращения каждого оставшегося кубика в 20 еще более мелких кубиков с размером в три раза меньше исходного про¬должается до бесконечности. В результате этих операций образуется идеально самоподобный объект, называемый губкой Менгера. Каж¬дая грань исходного куба выглядит при этом так же, как квадратный ковер Серпинского.
МАРТА.
СНЕЖИНКА КОХА
Процедура её построения показана на СЛАЙДЕ.
в начале берётся отрезок, делится на три равные части и средняя часть заменяется на два отрезка, равных изъятому. Получается ломаная из четырёх равных отрезков. На втором шаге действия повторятся с каждым из четырёх отрезков и получается ломаная из 16 отрезков.
Эти построения повторяются бесконечное число раз и в конце концов у нас получается ломаная, состоящая из бесконечного числа отрезков. Сколько бы мы её не масштабировали, мы всё равно будем получать одно и тоже. Это и есть звезда Коха.
Давайте теперь воспользуемся нашим приёмом, чтобы определить её размерность.
Из построения и рисунка видно, что звезду можно разбить на четыре равные части, при этом размер (длина исходного отрезка) каждой части будет равен трети размера исходной фигуры.
Кривые, представленные на СЛАЙДЕ называются кривыми Пеано, поскольку первая из них была построена Пеано в 1890 г.Их также называют заполняющими плоскость С математической точки зрения, кривая Пеано — всего лишь несколько необычное представление области или участка плоскости, а все классические определения единодушны в том, что размерность такого участка равна 2. Иными словами, человеку благоразумному следует избегать употребления термина кривая, заполняющая плоскость.
«Все шатается и рассыпается! Очень трудно передать словами тот эффект, который произвели результаты Пеано на все математическое сообщество. Такое ощущение, что кругом одни развалины, что все математические концепции внезапно потеряли всякий смысл» «Движение Пеано]невозможно представить себе интуитивно; его можно понять лишь с помощью логического анализа» . «Некоторые математические объекты — такие, например, как кривая Пеано — совершенно противоречат здравому смыслу... просто нелепы».
Я утверждаю, что приведенные цитаты лишь доказывают тот факт, что ни один из тех математиков так и не удосужился тщательно рассмотреть аккуратно построенную кривую Пеано. Кто-нибудь менее добродушный мог бы сказать, что эти цитаты демонстрируют полное отсутствие геометрического воображения.
КРИВЫЕ ПЕАНО - ЭТО КРИВЫЕ без самопересечений, терагоны которых избегают самокасаний. поговорим о кривых с умеренным числом самокасаний.
Изучая всевозможные терагоны Пеано, я обратилА внимание на то, что каждый из них представляет собой некоторую комбинацию из двух деревьев (или двух скоплений деревьев). Особенно хорошо эти деревья видны на «прохождении снежинки» — кривой Пеано. Глядя на рисунок, мы легко можем представить себе, что там изображено, скажем, скопление кустарников, растущих из нижней трети снежинки Коха и взбирающихся по ее стенкам. Другому эта картинка может показаться похожей на нарисованную плохо очиненным карандашом карту бассейна какой-нибудь большой реки — многочисленные мелкие притоки сливаются в более крупные и в конце концов вливаются в главную реку, протекающую вдоль нижней трети снежинки. ОТСЮДА следует, что кривые, отделяющие реки друг от друга, составляют в совокупности древовидный водораздел. Разумеется, реки и водоразделы могут меняться местами.
Последствия этого незначительного изменения выглядят весьма впечатляюще:
На этой иллюстрации нельзя различить саму кривую, мы видим лишь ее границу, которая называется кривой дракона. Таким образом, эта кривая Пеано имеет полное право называться прохождением дракона. Как и любая другая кривая Коха, инициатором которой служит отрезок , дракон самоподобен. Кроме того, отчетливо видно, что дракон разделен на части, соединяющиеся между собой тонкими переходами. Эти части подобны друг другу, но не целому дракону.
Двойной дракон.
Во «Фракталах» 1977 года отмечалось, что при таких «драконовских» правилах построения данной кривой более естественным инициатором представляется последовательность отрезков . Фигуру, которую в итоге заполняет кривая, я назвал двойным драконом. Выглядит она вот так (один дракон — черный, другой — серый):
Река двойного дракона. ЕСЛИ СТЕРЕТЬ мелкие притоки, получим древовидную реку двойного дракона:
Двойного дракона можно разбить на его уменьшенные подобия
Шкура двойного дракона ТАКЖЕ представляет собой кривую Коха
ЗВЯГИНЦЕВА ЛЕНА.
Дерево Пифагора —ЭТО разновидность фрактала, основанная на фигуре, известной как «Пифагоровы штаны».
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман во время второй мировой войны, используя обычную чертёжную линейку.
Одним из свойств дерева Пифагора является то, что, если площадь первого квадрата равна единице, то на каждом уровне сумма площадей квадратов тоже будет равна единице.
Если в классическом дереве Пифагора угол равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют обдуваемое ветром дерево Пифагора, которое является примером стохастического фрактала.
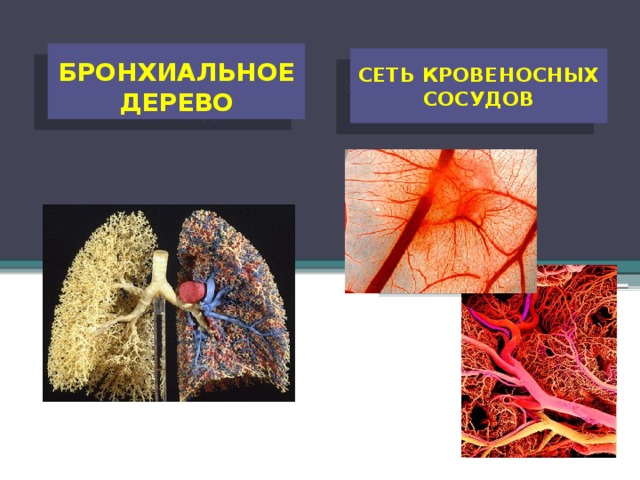
В природе фракталы ЕЩЕ мы можем наблюдать в тех случаях, когда посмотрим на:
Бронхиальное дерево
Сеть кровеносных сосудов
МолниЮ
Романеско – особый вид капусты броколли
ПАША.
Фрактальные антенны – относительно новый класс электрически малых антенн
Первой конструкцией фрактальной антенны с наиболее полно изученными электромагнитными и направленными свойствами стала антенна на основе префрактальной кривой Коха. Впервые применено использование фрактальной геометрии при проектировании антенных устройств было американским инженером Натаном Коэном. Он жил в то время в центре Бостона, где была запрещена установка на зданиях внешних антенн.
Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной.
В 1988 году, д-р Натан Коэн сделал первую в мире фрактальную антенну, после чего им в 1995 году была основана компания Fractal Antenna Systems, Inc. с целью коммерциализации своих дальнейших исследований в этой области. С тех пор признан одним из самых инновационных дизайнеров антенн, вследствие того, что фрактальной элемент антенны оказался гораздо более компактней, универсальней и мощней, чем традиционные конструкции антенн.
Фрактальная антенны с удивительно компактным дизайном обеспечивает превосходную широкополосную производительность в маленьком форм-факторе. Достаточно компактны для установки или встраивания в различных местах, фрактальные антенны используются для морских, воздушных транспортных средств, или персональных устройств.
Внутренняя антенна сотового телефона, выпускаемого в США, сделана на основе ковра Серпинского.
Текущие электронные системы наблюдения армии США используют фрактальные антенны, т.к. по сути своей, фрактальные антенны имеют низкий уровень шума и обеспечивают большую производительность, чем обычные антенны.
А в марте 2009 года, исследовательской группой раскрыто первая беспрецедентная возможность фрактальной геометрии в области маскировки (т.н. невидимость) для различных объектов военной промышленности. Компании, использующие и разрабатывающие маскировку для этих целей, стали использовать в слоях метаматериалов повторения, напоминающие фракталы. Используя слои меди, экспериментальный " контроль " продемонстрировал эффект рассеяния микроволн, используемых при обнаружении цели: было обнаружено, что рассеяние микроволн происходит не только при фронтальной направленности, но и по бокам и сзади объекта. Новейшие исследования подтверждают, что разброс микроволн происходит так, как будто препятствия не было совсем, что говорит о высокой эффективности использования фрактальных конструкции в сфере разведки и военной промышленности.
ФРАКТАЛЫ В ИНФОРМАТИКЕ
В компьютерной графике фракталы используются при создании изображений сложных, похожих на природные, объекты, например: деревьев, облаков, снега, береговых линий и др.
Алгебраические и стохастические — при построении ландшафтов, поверхности морей, карт раскраски, моделей биологических объектов и др.
ФРАКТАЛЫ В ЭКОНОМИКИ. ВИДЕО НА СЛАЙДЕ.
ГЕРЕЦ ВИКА.
Фракталы в народном творчестве
Мое внимание привлекла история всемирно известной игрушки «Матрешка». Присмотревшись внимательней, с уверенностью можно сказать, что эта игрушка-сувенир - типичный фрактал.
Принцип фрактальности очевиден, когда все фигурки деревянной игрушки выстроены в ряд, а не вложены друг в друга.
Мои небольшие исследования истории появления этого игрушечного фрактала на мировом рынке показали, что корни у этой красавицы – японские. Матрешка всегда считалась исконно русским сувениром. Но оказалось, что она прототип японской фигурки старика-мудреца Фукурума, привезенного когда-то в Москву из Японии.
Но именно российский игрушечный промысел принес этой японской фигурке мировую славу. Откуда возникла идея фрактальной вложенности игрушки, лично для меня, так и осталось загадкой. Скорей всего автор этой игрушки использовал принцип вложенности фигурок друг в друга. А самый простой способ вложения – это подобные фигурки разных размеров, а это уже - фрактал.
Не менее интересный объект исследования представляет собой роспись игрушки-фрактала. Это декоративная роспись – хохлома. Традиционные элементы хохломы – это травяные узоры из цветов, ягод и веток.
Снова все признаки фрактальности. Ведь один и тот же элемент можно повторять несколько раз в разных вариантах и пропорциях. В итоге получается народная фрактальная роспись.
И если новомодной росписью компьютерных мышек, крышек ноутбуков и телефонов никого уже не удивишь, то фрактальный тюнинг автомобиля в народном стиле – это что-то новое в автодизайне. Остается только удивляться проявлению мира фракталов в нашей жизни таким необычным образом в таких обычных для нас вещах.
ЛИДА.
Фракталы в дизайне мебели
Прагматичное использование принципа фрактальности продемонстрировал японский дизайнер Такеши Миякава.
Именно его фрактальная тумбочка стала первым примером использования фракталов в реальном мире, а не только в виртуальном.
Наверное, дизайнер Такеши Миякава (Takeshi Miyakawa) в детстве мечтал стать математиком. И его тоже занимала мысль о практическом использовании фракталов. Иначе как объяснить этот предмет мебели: тумбочка содержит 23 ящика самых разных размеров и пропорций, которые как-то ухитряются уживаться между собой внутри кубического корпуса, заполняя почти всё доступное им пространство.
Ни для кого не секрет, что японцы по жизни сильно ограничены в пространстве, в связи с чем, им приходится всячески изощряться в эффективном его использовании. Такеши Миякава показывает, как это можно делать одновременно эффективно и эстетично. Его фрактальный шкаф подтверждение тому, что использование фракталов в дизайне – это не только дань моде, но и гармоничное конструкторское решение в условиях ограниченного пространства.
Этот пример использования фракталов в реальной жизни, применительно к дизайну мебели показал мне, что фракталы реальны не только на бумаге в математических формулах и компьютерных программах. И, похоже, что принцип фрактальности природа использует повсеместно. Только нужно присмотреться к ней внимательней, и она проявит себя во всем своем великолепном изобилии и бесконечности бытия.
ШЕЙКО САША.
Августа Фердинанда Мебиуса
17 ноября 1790 года 215 лет назад в Германии родился мальчик – здоровый и крепкий малыш. Как и все дети, он сначала научился ползать, потом ходить, позже говорить. Все шло и развивалось своим чередом. Школа, университет. Мальчику повезло: астрономию ему преподавал сам Гаусс, математику – Пфафф. Как-то незаметно для окружающих в 26 лет он стал профессором, руководителем астрономической лаборатории в Лейпцигском университете. Научные статьи, лекции, работа. Все как у обычного профессора университета. Рассеянного доброго чудака студенты боготворили. Он любил ошарашивать их неожиданными задачками и назначал лекции, к примеру, на два часа ночи, чтобы показать ночное небо во всей его красе. Возможно, имя этого человека за 215 лет растворилось в истории, если бы ни одно ненастное утро…
На улице шел дождь. Была выкурена трубка, выпита чашка любимого кофе с молоком. Вид из окна навевал тоску. В кресле сидел мужчина. Мысли были разные, но как-то ничего особенного не приходило на ум. Только в воздухе витало ощущение, что именно этот день принесет славу и увековечит имя Августа Фердинанда Мебиуса.
На пороге комнаты появилась любимая жена. Правда, она была не в хорошем расположении духа. Правильнее сказать, она была разгневана, что для мирного дома Мебиусов было почти так же невероятно, как три раза в год увидеть парад планет, и категорически требовала немедленно уволить служанку, которая настолько бездарна, что даже не способна правильно сшить ленту.
Хмуро разглядывая злосчастную ленту, профессор воскликнул: “Ай да, Марта! Девочка не так уж глупа. Ведь это же односторонняя кольцевая поверхность. У ленточки нет изнанки!”
А в то же время…
Одновременно с Мёбиусом изобрел этот лист и другой ученик К. Ф. Гаусса —
Иоганн Бенедикт Листинг
(1808— 1882),
профессор Геттингенского университета.
Свою работу он опубликовал на три года раньше,
чем Мёбиус,— в 1862 году
А называется лента именем Мёбиуса
МАСТЕР-КЛАСС
ГОРСКАЯ
Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным.
Блез Паскаль
А Сейчас МЫ попробуЕМ доказать, что математика - очень увлекательная, интересная и полезная наука. Она может стать захватывающим занятием не только для СТУДЕНТОВ, но и для ПРЕПОДАВАТЕЛЕЙ и проведЕМ мастер –класс .
Основополагающий вопрос :
Можно ли подержать бесконечность в своих руках?
ЭКСПЕРИМЕНТ С БУМАГОЙ.
ЭКСПЕРИМЕНТ С ЖИЛЕТКОЙ.
Вывертывание жилета на изнанку, не снимая с человека.
Я попрошу одного из вас выйти ко мне. Одеваю на него жилет. Владельцу жилета необходимо сцепить пальцы рук за спиной. Пара движений, и жилет на нем одеваю изнаночной стороной.Кто –то хочет попробовать?
(Владельцу жилета необходимо сцепить пальцы рук за спиной. Окружающие должны вывернуть жилет наизнанку, не разнимая рук владельца. Для демонстрации этого опыта необходимо расстегнуть жилет и стянуть его по рукам за спину владельца. Жилет будет болтаться в воздухе, но, конечно, не снимется, потому что руки сцеплены. Теперь нужно взять левую полу жилета и, стараясь не измять жилет, просунуть ее как можно дальше в правую пройму. Затем взять правую пройму и просунуть ее в ту же пройму и в том же направлении. Осталось расправить жилет и натянуть его на владельца. Жилет окажется вывернутым на изнанку.)
ЭКСПЕРИМЕНТ С ШАРФОМ-ВЕРЕВКОЙ.
ВЫСТУПЛЕНИЕ СТУДЕНТОВ.
ПРИМЕНЕНИЕ ЛИСТА МЕБИУСА-СЛАЙДЫ
МАРУШКО.
СЛАЙД
"Где начало того конца, которым оканчивается начало?"
ГОРСКАЯ.
СЛАЙД.
Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.
А.Н. Крылов.
МАРУШКО .СЛАЙД.
ВЫВОД
Лист Мёбиуса – удивительный феномен.
Его можно исследовать до бесконечности, мы рассмотрели лишь некоторые его свойства. Надеемся, что мы вас заинтересовали и вы продолжите исследования этого непредсказуемого листа.
ГОРСКАЯ И МАРУШКО
СЛАЙД.
СВОЙСТВА ЛИСТА МЕБИУСА
Лист Мебиуса имеет один край, одну сторону
Лист Мёбиуса - топологический объект. Как и любая топологическая фигура, он не меняет своих свойств, пока его не разрезают, не разрывают или не склеивают его отдельные куски.
Один край и одна сторона листа Мебиуса не связаны с его положением в пространстве, не связаны с понятиями расстояния.
Лист Мёбиуса находит многочисленные применения в кулинарии, в технике, в физике, в живописи, в архитектуре, в оформлении ювелирных изделий и бижутерии.
Лента Мебиуса вдохновляет многих художников на создание известных скульптур и картин.
Чудесные свойства ленты порождают множество научных трудов, изобретений (весьма полезных и совершенно нереальных), а также множество фантастических рассказов.
СЛАЙД .ВЫВОД НА СЛАЙДЕ ЧЕРЕЗ ИНТЕРНЕТ ПРО ФРАКТАЛЫ
СЛАЙД. ВЫВОД ПО ЭМБЛЕМЕ МЕРОПРИЯТИЯ
СЛАЙД. СТИХ НА СЛАЙДЕ + ПЕСНЯ «АВЕ МАРИЯ»
ПОДВЕДЕНИЕ ИТОГОВ МЕРОПРИЯТИЯ
ГОРСКАЯ. «Мышление начинается с удивления»,- заметил 2500 лет назад Аристотель. Наш современник Сухомлинский считал», что чувство удивления – могучий источник желания знать: от удивления к знаниям – один шаг». А математика И ФИЗИКА замечательный предмет для удивления.
МАРУШКО. Именно это МЫ попыталИСЬ показать в ИССЛЕДОВАТЕЛЬСКОЙ работе, описывая ФРАКТАЛЫ, лист Мёбиуса и процесс его изготовления, раскрывая опытным путём свойства этого поразительного открытия. НАШЕ предположение подтвердилось: лента Мёбиуса обладает не только свойством односторонности, но и такими, действительно, неожиданными свойствами, как непрерывность и связность.
ГОРСКАЯ Знания о листе Мёбиуса имеют и практическое значение в жизни человека. МЫ постаралИСЬ показать ,что односторонность листа Мебиуса нашла отражение в технике, в природе, в науке, в искусстве. Представленная в работе односторонность листа Мебиуса уже увековечена в памяти людей : памятники листу Мебиуса в разных странах, картины Эшера поражающие воображение , технические изобретения , именем Мебиуса назван кратер на обратной стороне поверхности Луны.
Одним из примеров ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ явились работы, которые представлены на Всероссийский открытый заочный конкурс достижений талантливой молодежи "НАЦИОНАЛЬНОЕ ДОСТИЖЕНИЕ РОССИИ" 2011-2012г.г.. Научный руководитель - преподаватель математики Горская Наталия Владимировна
Победители заочного отборочного тура - лауреаты I сессии ЗАОЧНОГО ТУРА VI ЕЖЕГОДНОГО ВСЕРОССИЙСКОГО КОНКУРСА ДОСТИЖЕНИЙ ТАЛАНТЛИВОЙ МОЛОДЁЖИ "НАЦИОНАЛЬНОЕ ДОСТОЯНИЕ РОССИИ":
Баранов Владислав Олегович, студент группы 12 ТЕХ
Смородин Андрей Владимирович, студент группы 13 ТЕХ ТЕМА ФРАКТАЛЫ
Муха Софья Вячеславовна, студентка группы 13 ТЕХ
Касацкая Елена Вячеславовна, студентка группы 1 ЮТ ТЕМА ЛИСТ МЕБИУСА
и Федотова Ксения Александровна, студентка группы 1 ЮТ
МАРУШКО . Вот и подошла к концу наша экскурсия в мир фракталов И ЛИСТА МЕБИУСА. НадеЕМСЯ она Вам понравилась. МЫ только немного приоткрылИ Вам завесу в мир НЕВОЗМОЖНОГО.
ГОРСКАЯ
Невозможно – это всего лишь громкое слово, за которым прячутся маленькие люди.
МАРУШКО
Им проще жить в привычном мире, чем найти в себе силы что-то изменить.
ГОРСКАЯ
Невозможное – это не факт. Это только мнение.
МАРУШКО
Невозможное – это не приговор. Это вызов.
ГОРСКАЯ
Невозможное – это шанс проявить себя.
МАРУШКО
Невозможное – это не навсегда.
ВМЕСТЕ: Невозможное возможно!
САМОАНАЛИЗ
Рассмотрение данной темы ИССЛЕДОВАНИЯ позволяет решать след задачи:
1.Учить анализировать, рассуждать, делать выводы.
2.Учит видеть связь математикиИ ДРУГИХ ДИСЦИПЛИН с жизнью.
3.Учит видеть прекрасное..
4.Способствует повышению интереса СТУДЕНТОВ к математике. Ведь интерес в обучении окрыляет, помогает преодолевать трудности, пробуждает любовь к ДИСЦИПЛИНЕ,а достигается это
через занимательность и привлекательность задач,
через видение внутренней красоты математики, ее изящности и неповторимости,
через изучение страниц истории, связанных как с именами великих математиков и философов, так и с появлением новых терминов, положений, математических законов, теорем,
через доступность и понятность изучаемого материала.
ПРЕПОДОВАТЕЛЯМ нужно смотреть «за страницы математики» и открывать туда путь своим СТУДЕНТАМ ЧЕРЕЗ .
14
 АЛИНИНГРАДСКИЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ
АЛИНИНГРАДСКИЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ