Данная презентация рассчитана. для учащихся 9 кеклассных мероприятий. В презентации представлены слайды с различными видами уравнений, а также с разными видами работ на уроке. Её могут использовать учителя математики для повышения интереса к предмету во время устной работы, самостоятельной работы с последующей проверкой. Работа может быть использована как опытными учителями, так и молодыми специалистами, не имеющими пока большого количества своих наработок. Очень важно, чтобы учащиеся изучали математику не только потому, что это нужно для ОГЭ и ЕГЭ, но и потому, что им нравится математика, им интересно её изучать. Задания данной презентации помогут учителям развить интерес ребят к этому предмету.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
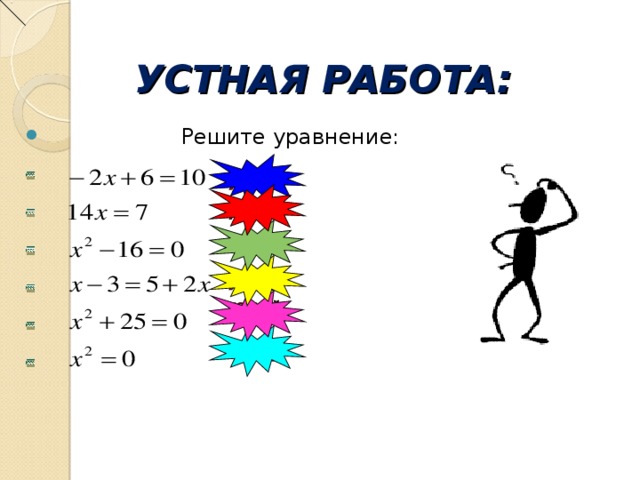
Презентация по теме " Решение уравнений для подготовки к ОГЭ"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Презентация по теме " Решение уравнений для подготовки к ОГЭ" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1790 руб.
2560 руб.
2000 руб.
2860 руб.
1900 руб.
2710 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства








 0 , значит, 2 корня. 2) D ,значит, нет корней. 3) D =0,значит, 1 корень." width="640"
0 , значит, 2 корня. 2) D ,значит, нет корней. 3) D =0,значит, 1 корень." width="640"


 0. t 2 -5 t+ 4 =0 D= 25-16 = 9 t 1 = 4 t 2 = 1 Значит, х 2 = 4 или х 2 = 1 x=± 2 x=± 1 Ответ: -2; 2; -1; 1. х 4 -5х 2 +4=0" width="640"
0. t 2 -5 t+ 4 =0 D= 25-16 = 9 t 1 = 4 t 2 = 1 Значит, х 2 = 4 или х 2 = 1 x=± 2 x=± 1 Ответ: -2; 2; -1; 1. х 4 -5х 2 +4=0" width="640"


















