Презентация к уроку геометрии в 9 классе на тему "Координаты вектора". Урок объяснения нового материала.
Цели:
- Образовательная:
- изучение и первичное осознание нового учебного материала,
- осмысление связей и отношений в объектах изучения.
- Развивающая: развивать пространственное воображение, умение анализировать.
- Воспитательные:
- воспитывать умение осмысленно слушать,
- привитие аккуратности в исполнении геометрического чертежа,
- воспитание честности.
Задачи:
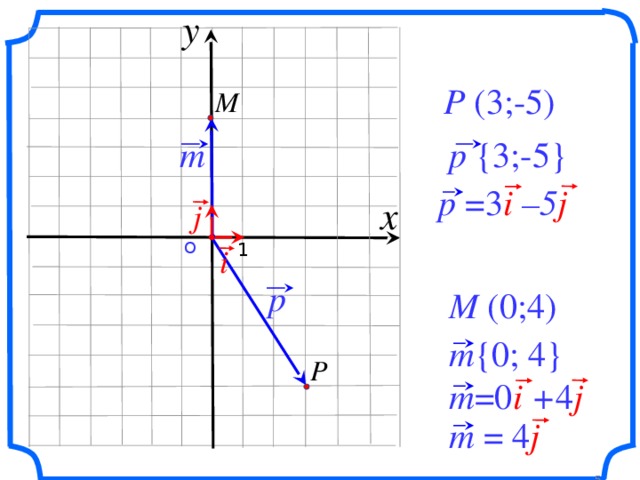
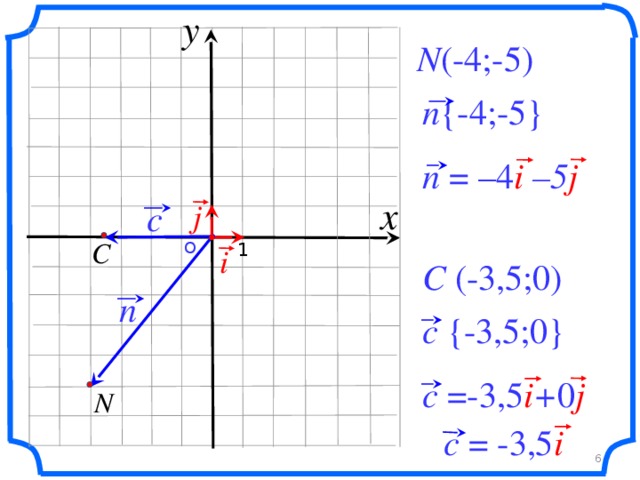
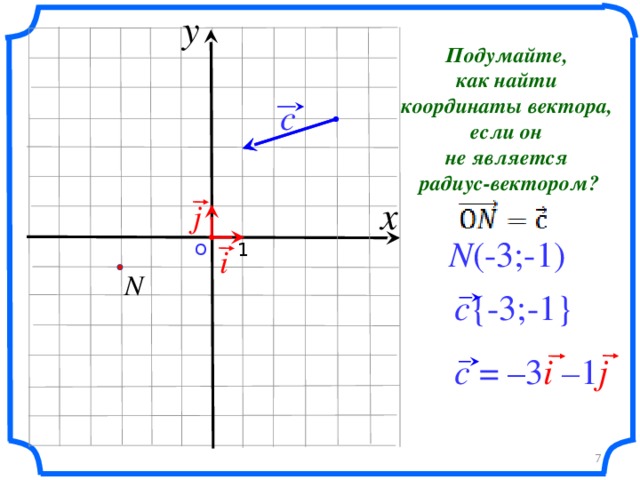
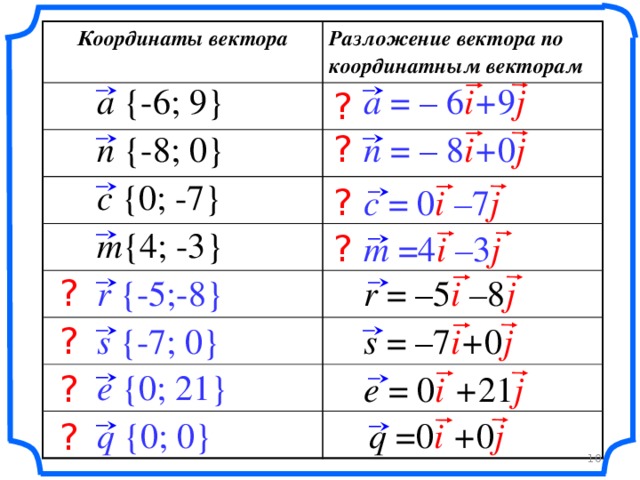
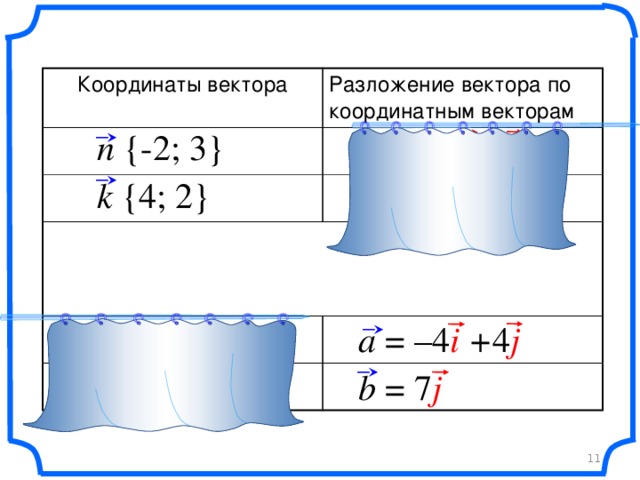
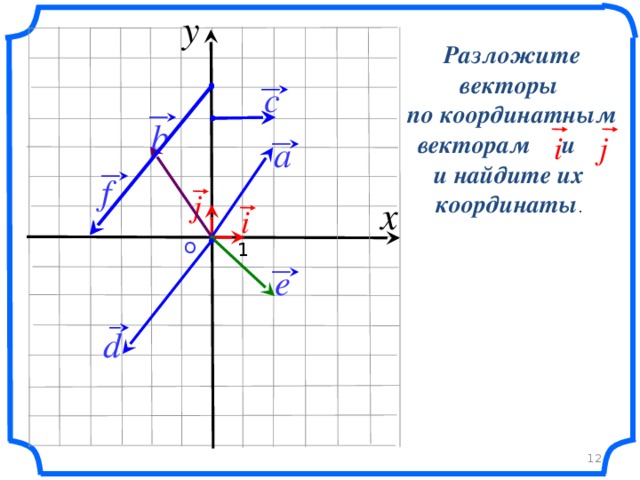
- Дать понятия: единичные координатные векторы, координаты вектора, разложение вектора по единичным векторам i и j;
- показать образцы оформления записей;
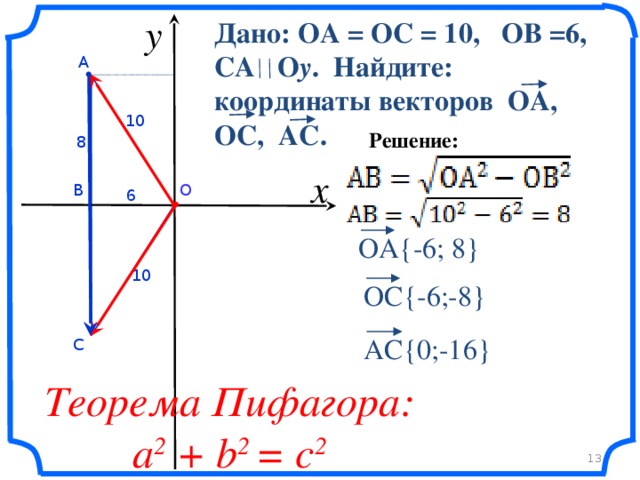
- отработать полученные знания на примерах;



 ОВ = -6i + 2j = c = 5i – 3j = 0 = o∙ i + o∙ j = В прямоугольной системе координат отложим от точки О единичные векторы i и j" width="640"
ОВ = -6i + 2j = c = 5i – 3j = 0 = o∙ i + o∙ j = В прямоугольной системе координат отложим от точки О единичные векторы i и j" width="640"