Адаптированная рабочая программа по математике для учащихся 8 класса с ЗПР
- Меню
- Главная
- Дошкольное образование
- Начальные классы
- Астрономия
- Биология
- География
- Информатика
- Математика
- Алгебра
- Геометрия
- Химия
- Физика
- Русский язык
- Английский язык
- Немецкий язык
- Французский язык
- История
- Естествознание
- Всемирная история
- Всеобщая история
- История России
- Право
- Окружающий мир
- Обществознание
- Экология
- Искусство
- Литература
- Музыка
- Технология (мальчики)
- Технология (девочки)
- Труд (технология)
- Физкультура
- ИЗО
- МХК
- ОБЗР (ОБЖ)
- Внеурочная работа
- ОРК
- Директору
- Завучу
- Классному руководителю
- Экономика
- Финансовая грамотность
- Психологу
- ОРКиСЭ
- Школьному библиотекарю
- Логопедия
- Коррекционная школа
- Всем учителям
- Прочее
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
- Главная
- Математика
- Планирование
- Адаптированная рабочая программа по математике для учащихся 8 класса с ЗПР
Адаптированная рабочая программа по математике для учащихся 8 класса с ЗПР
Просмотр содержимого документа
«Адаптированная рабочая программа по математике для учащихся 8 класса с ЗПР»

по математике для учащихся 8 класса с ЗПР
Составила Бурова Светлана Юрьевна учитель математики первой квалификационной категории
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по математике для 8 класса составлена на основе примерной программы основного общего образования по математике и Федерального компонента государственного стандарта основного общего образования. Программа составлена на 170 часов в соответствии с учебным планом школы. .Предмет математика представлен двумя дисциплинами: алгебра и геометрия. Базисный план на изучение математики в основной школе отводит 5 учебных часов: 3 часа на алгебру (102 часа), 2 часа на геометрию (68 часов).
В программу внесены следующие изменения:
при рассмотрении простейших геометрических фигур, все понятия вводятся на наглядной основе;
аксиомы даются через решение задач и приводятся в описательной форме;
теоремы даются без доказательств, так как они трудны для учащихся с задержкой психического развития.
Внесение данных изменений позволит охватить весь изучаемый материал по программе, повысить уровень обученности учащихся по предмету, а также более эффективно осуществить индивидуальный подход к обучающимся.
Все основные понятия вводятся на наглядной основе. Аксиомы даются в процессе практических упражнений через решение задач и приводятся в описательной форме. Все теоретические положения даются исключительно в ознакомительном плане и опираются на наглядные представления учащихся.
Программа построена с учетом специфики усвоения учебного материала детьми, испытывающими трудности в обучении, причиной которых являются различного характера задержки психического развития: недостаточность внимания, памяти, логического мышления, пространственной ориентировки, быстрая утомляемость отрицательно влияют на усвоение математических понятий, в связи с этим при рассмотрении курса математики 8 класса были внесены изменения в объем теоретических сведений для этих детей. Некоторый материал программы им дается без доказательств, только в виде формул и алгоритмов или ознакомительно для обзорного изучения, некоторые темы в связи со сложностью изложения и понимания для детей с ЗПР были исключены.Учитывая нарушение процессов запоминания и сохранения информатизации у детей с ЗПР, пришлось следующие темы (смотрите примечание к планированию) изучать ознакомительно с опорой на наглядность.Снизив объем запоминаемой информации, для учащихся с ЗПР целесообразно более широко ввести употребление опорных схем, памяток, алгоритмов.
Данная программа для детей с ЗПР откорректирована в направлении разгрузки курса по содержанию, т.е. предполагается изучение материала в несколько облегченном варианте, однако не опускается ниже государственного уровня обязательных требований.
Примечание к планированию математики
Темы изучаются как ознакомительные.
Глава «Рациональные дроби».
Темы: «Функция у=k/x и ее график», «Функция у = √х и ее график».
Глава «Формулы корней квадратного уравнения».
Тема: «Элементы статистики».
Глава «Действительные числа».
Темы: «Иррациональные числа», «Нахождение приближенных значений квадратного корня».
Глава «Степень с целым показателем и ее свойства».
Темы: «Стандартный вид числа», «Приближенные вычисления».
Глава «Квадратные уравнения».
Темы: «Решение квадратных уравнений, выделением квадрата двучлена», «Вывод формулы корней квадратного уравнения», «Преобразование выражений, содержащих квадратные корни в знаменателе дроби», «Теорема Виета».
Глава «Четырехугольники».
Тема: «Признаки параллелограмма», «Теорема Фалеса».
Глава «Площадь».
Тема: «Площадь квадрата».
Глава «Подобные треугольники».
Тема: «Практические приложения подобия треугольников».
Глава «Окружность».
Темы: «Градусная мера дуги окружности», «Теорема о вписанном угле».
Изучение математики для детей с ЗПР направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
развитиевысших психических функций, умение ориентироваться в задании, анализировать его, обдумывать и планировать предстоящую деятельность.
Темп изучения материала для детей с ЗПР должен быть небыстрый. Достаточно много времени отводится на отработку основных умений и навыков, отвечающих обязательным требованиям, на повторение, в том числе коррекцию знаний за курс математики предыдущих классов. Отработка основных умений и навыков осуществляется на большом числе посильных учащимся упражнений. Но задания должны быть разнообразны по форме и содержанию, включать в себя игровые моменты.
Формирование важнейших умений и навыков происходит на фоне развития продуктивной умственной деятельности: обучающиеся учатся анализировать, замечать существенное, подмечать общее, делать несложные выводы и обобщения, переносить несложные приемы в нестандартные ситуации, обучаются логическому мышлению, приемам организации мыслительной деятельности.
Важнейшее условие правильного построения учебного процесса - это доступность и эффективность обучения для каждого учащегося в классе, что достигается выделением в каждой теме главного, и дифференциацией материала, отработкой на практике полученных знаний.
Во время учебного процесса нужно иметь в виду, что учебная деятельность должна быть богатой по содержанию, требующей от школьника интеллектуального напряжения, но одновременно обязательные требования не должны быть перегруженными по обхвату материала и доступны ребенку. Только доступность и понимание помогут вызвать у таких учащихся интерес к учению. Немаловажным фактором в обучении таких детей является доброжелательная, спокойная атмосфера, атмосфера доброты и понимания.
Принцип работы в данном классе - это и речевое развитие, что ведет непосредственным образом к интеллектуальному развитию: учащиеся должны проговаривать ход своих рассуждений, пояснять свои действия при решении различных заданий.Выполнение письменных заданий предваряется анализом языкового материала с целью предупреждения ошибок.
Особенностью организации учебного процесса по данному курсу является выбор разнообразных видов деятельности с учетом психофизических особенностей обучающихся, использование занимательного материала, включение в урок игровых ситуаций, направленных на снятие напряжения, переключение внимания детей с одного задания на другое и т. п. Особое внимание уделяется индивидуализации обучения и дифференцированному подходу в проведении занятий.
Важнейшими коррекционными задачами курса геометрии являются развитие логического мышления и речи учащихся, формирование у них навыков умственного труда — планирование работы, поиск рациональ-ныхпутей ее выполнения, осуществление самоконтроля. Школьники должны научиться грамотно и аккуратно делать математические записи,уметь объяснить их. Дети с ЗПР из-за особенностей своего психического развития трудно усваивают программу по геометрии, так как затруднено логическое мышление, образное представление.
Усвоение материала будет более эффективным, если умственная деятельность будет сочетаться с практической. Как и на уроках других предметов, важным является развитие речи учащихся. Поэтому любой записываемый материал должен проговариваться. Учащиеся должны объяснять действия, вслух высказывать свои мысли, мнения, ссылаться на известные правила, факты, предлагать способы решения, задавать вопросы. Большое значение в процессе обучения и развития учащихся имеет решение задач. В большинстве задачи решаются на готовых чертежах. Пересказ условия задачи своими словами помогает удержать эти условия в памяти. Следует поощрять также решение разными способами. Таким образом, доступная, интересная деятельность, ощущение успеха, доброжелательные отношения являются непременным условием эффективной работы с детьми ЗПР.
Все основные понятия вводятся на наглядной основе. Аксиомы даются в процессе практических упражнений через решение задач и приводятся в описательной форме. Все теоретические положения даются исключительно в ознакомительном плане и опираются на наглядные представления учащихся,
Очень много устных задач по готовым чертежам, часто проводятся математические диктанты, графические диктанты, Работы плана «Дочерти», «Объясни», «Найди соответствие» и другие.
Форма организации образовательного процесса: классно-урочная.
Технологии, используемые в обучении: обучение в сотрудничестве, развивающего обучения, информационно - коммуникационные, здоровьесбережения.
СОДЕРЖАНИЕ УЧЕБНОГО КУРСА ПО АЛГЕБРЕ ДЛЯ УЧАЩИХСЯ С ЗПР
Основное свойство дроби. Сокращение дробей. Сложение и вычитание дробей с одинаковыми и разными знаменателями. Умножение и деление дробей, возведение дробей в степень. Свойства функции у = 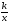 рассматривать на конкретных графиках (ознакомительно).
рассматривать на конкретных графиках (ознакомительно).
Понятие об иррациональном числе (ознакомительно). Общие сведения о действительных числах (ознакомительно). Понятие арифметического квадратного корня. Уравнение х2=а, свойства квадратных корней. Преобразование выражений, содержащих квадратные корни. Функция у =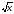 , ее график (ознакомительно).
, ее график (ознакомительно).
Определение квадратного уравнения. Решение квадратных уравнений по формуле. Решение несложных задач с помощью квадратных уравнений. Решение дробно-рациональных уравнений.
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке выражений х + у, ху. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной.
Степень с целым показателем и ее свойства. Стандартный вид числа.Элементы комбинаторики и статистики (ознакомительно).
Повторение.
СОДЕРЖАНИЕ УЧЕБНОГО КУРСА ПО ГЕОМЕТРИИ ДЛЯ УЧАЩИХСЯ С ЗПР
Многоугольники. Параллелограмм. Признаки параллелограмма(ознакомительно).Трапеция.Прямоугольник, квадрат, ромб. Теорема Фалеса (ознакомительно).
Понятие о площади плоских фигур.Площадь квадрата (ознакомительно).Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции. Теорема Пифагора.
Подобие треугольников, коэффициент подобия, признаки подобия треугольников.Средняя линия треугольника. Практические приложения подобия треугольников(ознакомительно).
Синус, косинус, тангенс острого угла прямоугольного треугольника.Решение прямоугольных треугольников.
Взаимное расположение прямой и окружности. Касательная и секущая к окружности, равенство касательных, проведенных из одной точки. Центральные и вписанные углы. Теорема о вписанном угле(ознакомительно).Метрические соотношения в окружности: свойства секущих, касательных, хорд.
Четыре замечательные точки треугольника: точки пересечения серединных перпендикуляров, биссектрис, медиан.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника.
Понятие вектора. Равенство векторов. Откладывание вектора от данной точки. Сложение и вычитание векторов. Произведение вектора на число.
Повторение.
ОСНОВНОЕ СОДЕРЖАНИЕ
С РАСПРЕДЕЛЕНИЕМ УЧЕБНЫХ ЧАСОВ ПО РАЗДЕЛАМ КУРСА
Алгебра
| № урока |
Тема урока | Кол-во часов | Элементы содержания образования |
Основные понятия |
Знания, умения | Дата | ||||
| Глава 1: РАЦИОНАЛЬНЫЕ ДРОБИ (23ч) |
| |||||||||
| 1/1 | Рациональные выражения |
2 | Вести понятие дробных выражений; выработать и закрепить алгоритм нахождения допустимых значений | Дробные выражения, допустимые значения переменной, рациональные дроби | Знать: определение дробных выражений, алгоритм нахождения допустимых значений Уметь: находить допустимые значения переменных |
| ||||
| 2/2 | Допустимые значения переменной |
|
| |||||||
| 3/3 | Основное свойство дроби |
3 | Доказать основное свойство дроби и научить применять его при сокращении дробей и приведения дробей к новому знаменателю | Основное свойство дроби, тождество | Знать: в чем заключается основное свойство дроби; что такое тождество. Уметь: выполнять приведение дроби к новому знаменателю и сокращать дроби |
| ||||
| 4/4 | Сокращение дробей |
| ||||||||
| 5/5 | Решение заданий на сокращение дробей |
|
| |||||||
| 6/6 | Сложение и вычитание дробей с одинаковыми знаменателями | 1 | Научить складывать и вычитать алгебраические дроби с одинаковыми знаменателями |
| Знать: правила сложения и вычитания дробей с одинаковыми знаменателями Уметь: складывать и вычитать дроби с одинаковыми знаменателями |
| ||||
| 7/7 | Правило сложения и вычитания дробей с разными знаменателями |
3 | Научить находить общий знаменатель двух дробей, сформировать навыки сложения и вычитания дробей |
| Знать: как находить общий знаменатель Уметь: складывать и вычитать дроби с разными знаменателями, применять полученные знания к решению заданий на упрощение выражений |
| ||||
| 8/8 | Решение заданий на сложение и вычитание дробей с разными знаменателями |
|
| |||||||
| 9/9 | Повторение темы «Сокращение, сложение и вычитание дробей» |
|
| |||||||
| 10/10 | Подготовка к к/р по теме «Сокращение, сложение и вычитание дробей» | 1 | Обобщить и систематизировать знания по теме |
| Знать: алгоритм нахождения допустимых значений, в чем заключается основное свойство дроби; правила сложения и вычитания дробей с одинаковыми знаменателями и разными знаменателями; Уметь: находить допустимые значения переменных, выполнять приведение дроби к новому знаменателю и сокращать дроби; складывать и вычитать дроби с разными знаменателями, применять полученные знания к решению заданий на упрощение выражений |
| ||||
| 11/11 | К/р №1 по теме «Сокращение, сложение и вычитание дробей» | 1 | Проверка ЗУН |
|
|
| ||||
| 12/12 | Умножение дробей |
3 | Выработать умение умножать дроби |
| Знать: правила умножения дробей и возведение дробей в степень; Уметь: перемножать дроби и возводить их в степень; применять полученные навыки к упрощению выражений |
| ||||
| 13/13 | Возведение дробей в степень | Выработать умение возводить дробь в степень |
|
| ||||||
| 14/14 | Решение заданий на умножение и возведение дробей в степень | Закрепить умения |
|
| ||||||
| 15/15 | Деление дробей |
2 | Научить преобразовывать частное рациональных дробей в дробь, закрепить умения делить дробь на дробь, сокращать дроби. |
| Знать: правило деления рациональных дробей; Уметь: делить дробь на дробь, сокращать дроби. |
| ||||
| 16/16 | Решение заданий на деление дробей |
|
| |||||||
| 17/17 | Преобразование рациональных выражений |
2 | Выработать умения выполнять тождественные преобразования рациональных выражений и закрепить их |
| Знать: что представляет собой рациональное выражения; Уметь: выполнять тождественные преобразования рациональных выражений |
| ||||
| 18/18 | Упрощение рациональных выражений |
|
| |||||||
| 19/19 | Функция у = k/х и её график |
2 | Познакомить с функцией у = k/х, её свойствами и графиком | Обратная пропорциональность, гипербола | Знать: определение и свойства обратной пропорциональности, что является графиком обратной пропорциональности; Уметь: строить график обратной пропорциональности. |
| ||||
| 20/20 | Построение графика функции у = k/х |
| ||||||||
| 21/21
| Повторение темы «Преобразование рациональных выражений» |
2 | Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: правила умножения, деления дробей и возведение дробей в степень; Уметь: перемножать, делить дроби и возводить их в степень; применять полученные навыки к упрощению выражений; выполнять тождественные преобразования рациональных выражений |
| ||||
| 22/22 | Подготовка к к/р по теме «Преобразование рациональных выражений» |
|
| |||||||
| 23/23 | К/р №2 «Преобразование рациональных выражений» | 1 | Проверка ЗУН |
|
|
| ||||
| Глава 2: КВАДРАТНЫЕ КОРНИ (20 ч) |
| |||||||||
| 1/24 | Рациональные числа | 1 | Расширить и обобщить понятие числа, дать сведения о рациональных числах, познакомить с представлением рациональных чисел в виде десятичной дроби | Рациональные числа | Знать: какие числа составляют множество рациональных чисел; Уметь: представлять рациональное число в виде бесконечной десятичной периодической дроби |
| ||||
| 2/25 | Иррациональные числа | 1 | Сформировать представление о множестве действительных чисел | Иррациональные числа | Знать: какие числа составляют множество действительных чисел; Уметь: среди данных чисел выбирать рациональные и иррациональные числа, сравнивать их |
| ||||
| 3/26
| Арифметический квадратный корень |
2 | Дать понятие о квадратном корне из числа | Квадратный корень, арифметический квадратный корень, подкоренное выражение | Знать: определения квадратного корня и арифметического квадратного корня; Уметь: находить значение корня. |
| ||||
| 4/27 | Уравнение х2=а | 1 | Научить решать уравнение вида х2=a, (х – а)2 = m |
| Знать: три случая решения уравнения х2 = а Уметь: решать уравнение вида х2=a, (х – а)2 = m |
| ||||
| 5/28 | Нахождение приближенных значений квадратного корня | 1 | Научить находить для любого иррационального числа вида √а, где а›0 две последовательные десятичные дроби, между которыми заключено это число |
| Уметь: находить для любого иррационального числа вида √а, где а›0 две последовательные десятичные дроби, между которыми заключено это число |
| ||||
| 6/29 | Функция у = √х и её график |
2 | Познакомить с функцией у = √х, её свойствами и графиком |
| Знать: свойства функции у = √х, правила нахождения значения функции и аргумента по графику; Уметь: строить график функции у = √х, находить значения функции и аргумента по графику; |
| ||||
| 7/30 | Построение графика функции у = √х |
|
| |||||||
| 8/31 | Квадратный корень из произведения |
2 | Сформулировать свойства арифметического квадратного корня, научить применять свойства корней к решению заданий |
| Знать: чему равен корень из произведения и корень из дроби; Уметь: находить корень из произведения и из дроби |
| ||||
| 9/32 | Квадратный корень из дроби | |
| |||||||
| 10/33 | Квадратный корень из степени |
1 | Сформулировать свойство корня из степени, научить применять это свойство |
| Знать: формулу корня из степени Уметь: применять эту формулу к решению заданий |
| ||||
| 11/34 | Подготовка к к/р по теме «Определение и свойства арифметического квадратного корня» |
1 | Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: определения квадратного корня и арифметического квадратного корня; три случая решения уравнения х2 = а; чему равен корень из произведения и корень из дроби; формулу корня из степени. Уметь: находить значение корня, решать уравнение вида х2=a, (х – а)2 = m, находить корень из произведения, из дроби, из степени |
| ||||
| 12/35 | К/р №3 «Определение и свойства арифметического квадратного корня» |
1 | Проверка ЗУН |
|
|
| ||||
| 13/36 | Вынесение множителя из-под знака корня. |
3
| Научить выносить множитель из-под знака корня |
| Знать: как выносится множитель из-под знака корня. Уметь: выносить множитель из-под знака корня |
| ||||
| 14/37 | Внесение множителя под знак корня | Научить вносить множитель под знак корня |
| Знать: как вносится множитель под знак корня Уметь: вносить множитель под знак корня |
| |||||
| 15/38 | Решение заданий на вынесение и внесение множителя | Закрепить умения вносить под знак корня и выносить из-под знака корня множитель |
| Знать: как выносится множитель из-под знака корня и как вносится множитель под знак корня Уметь: выносить множитель из-под знака корня, выносить множитель из-под знака корня, вносить множитель под знак корня |
| |||||
| 16/39 | Преобразование выражений, содержащих квадратный корень |
3 | Сформировать умения преобразования корней из произведения, дроби и степени, умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня, избавление от иррациональности в знаменателе
|
| Уметь: делать преобразования корней из произведения, дроби и степени, умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня, избавление от иррациональности в знаменателе |
| ||||
| 17/40 | Разложение на множители выражений, содержащих квадратный корень |
|
| |||||||
| 18/41 | Избавление от иррациональности в знаменателе |
|
| |||||||
| 19/42 | Подготовка к к/р по теме «Квадратные корни» |
1 | Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: как выносится множитель из-под знака корня и как вносится множитель под знак корня Уметь: делать преобразования корней из произведения, дроби и степени, умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня, избавление от иррациональности в знаменателе |
| ||||
| 20/43 | К/р №4 по теме: «Квадратные корни» | 1 | Проверка ЗУН |
|
|
| ||||
| Глава 3: КВАДРАТНЫЕ УРАВНЕНИЯ И ЕГО КОРНИ (22ч) |
| |||||||||
| 1/44 | Определение квадратного уравнения |
2 | Дать определение квадратного уравнения, ввести понятие неполных квадратных уравнений и научить решать неполные квадратные уравнения | Квадратное уравнение, приведенное квадратное уравнение | Знать: определения квадратного уравнения, неполного квадратного уравнения, приведенного квадратного уравнения Уметь: решать неполные квадратные уравнения |
| ||||
| 2/45 | Неполные квадратные уравнения | Неполное квадратное уравнение |
| |||||||
| 3/46 | Решение квадратных уравнений выделением квадрата двучлена | 1 | Показать, как решаются уравнения путем выделения из трехчлена квадрата двучлена |
| Уметь: решать уравнения путем выделения из трехчлена квадрата двучлена |
| ||||
| 4/47 | Формула корней квадратного уравнения |
3 | Научить решать квадратное уравнение с помощью формулы, уметь определять количество корней квадратного уравнения в зависимости от дискриминанта | Х1,2 = Дискриминант D D = b2 – 4ac | Знать: формулу вычисления дискриминанта, формулу корней квадратного уравнения, как зависит количество корней квадратного уравнения от дискриминанта; Уметь: решать квадратное уравнение с помощью формулы; определять количество корней квадратного уравнения в зависимости от дискриминанта |
| ||||
| 5/48 | Решение квадратных уравнений по формуле |
| ||||||||
| 6/49 | Решение уравнений, сводящихся к квадратным |
| ||||||||
| 7/50 | Составление квадратного уравнения по условию задачи |
3 | Научить и закрепить составлять уравнение по условию задачи; научить определять, соответствуют ли найденные корни условию задачи |
| Уметь: составлять уравнения по условию задачи; определять, соответствуют ли найденные корни условию задачи |
| ||||
| 8/51 | Решение задач с помощью квадратных уравнений |
|
| |||||||
| 9/52 | Решение задач с помощью квадратных уравнений |
|
| |||||||
| 10/53 | Теорема Виета |
3 | Сформулировать теорему Виета, научить применять её и обратную ей при решении задач разной степени трудности | x2 + px + q =0 х1 + х2 = -p, х1 ∙ х2 = q | Знать: теорему Виета и теорему, обратную ей. Уметь: применять её и обратную ей при решении задач разной степени трудности |
| ||||
| 11/54 | Теорема, обратная теореме Виета |
| ||||||||
| 12/55 | Решение приведенных квадратных уравнений |
| ||||||||
| 13/56 | Подготовка к к/р по теме «Квадратные уравнения» |
| Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: определения квадратного уравнения, неполного квадратного уравнения, приведенного квадратного уравнения; формулу вычисления дискриминанта, формулу корней квадратного уравнения, как зависит количество корней квадратного уравнения от дискриминанта; теорему Виета и теорему, обратную ей. Уметь: решать неполные квадратные уравнения; решать квадратное уравнение с помощью формулы; определять количество корней квадратного уравнения в зависимости от дискриминанта; составлять уравнения по условию задачи; определять, соответствуют ли найденные корни условию задачи. |
| ||||
| 14/57 | К/р №5 по теме: «Квадратные уравнения» | 1 | Проверка ЗУН |
|
|
| ||||
| 15/58 | Дробные рациональные уравнения |
3 | Дать определение дробных рациональных уравнений, сформировать умение решать дробные рациональные уравнения | Дробные рациональные уравнения, правила решения таких уравнений | Знать: определение дробных рациональных уравнений, правила решения рациональных уравнений Уметь: решать дробные рациональные уравнения |
| ||||
| 16/59 | Решение дробных рациональных уравнений |
|
| |||||||
| 17/60 | Графический способ решения уравнений | Ознакомить учащихся с графическим способом решения уравнений. | Знать: как решаются уравнения графическим способом Уметь: решать уравнения с помощью графиков |
| ||||||
| 18/61 | Составление рационального уравнения по условию задачи |
3 | Обучение составлению дробных рациональных уравнений по условию задачи |
| Уметь: составлять дробные рациональные уравнения по условию задачи |
| ||||
| 19/62 | Решение задач с помощью рациональных уравнений на движение |
|
| |||||||
| 20/63 | Решение задач с процентами с помощью рациональных уравнений |
|
| |||||||
| 21/64 | Подготовка к к/р по теме «Дробные иррациональные уравнения» |
1 | Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: теоретический материал по данному разделу; Уметь: применять полученные знания к решению заданий |
| ||||
| 22/65 | К/р №6 по теме: «Дробные иррациональные уравнения» | 1 | Проверка ЗУН |
|
|
| ||||
| Глава 4: НЕРАВЕНСТВА (18ч) |
| |||||||||
| 1/66 | Определение числовых неравенств |
2 | Сформулировать определение числовых неравенств, научить использовать его в доказательстве неравенств |
| Знать: определение числовых неравенств Уметь: применять определение к доказательству неравенств. |
| ||||
| 2/67 | Доказательство числовых неравенств |
|
| |||||||
| 3/68 | Свойства числовых неравенств |
1 | Сформулировать и доказать свойства числовых неравенств, научить иллюстрировать эти свойства на координатной прямой |
| Знать: свойства числовых неравенств Уметь: применять эти свойства при решении неравенств, иллюстрировать эти свойства на координатной прямой |
| ||||
| 4/69 | Сложение числовых неравенств |
2 | Рассмотреть, как выполняется сложение и вычитание числовых неравенств |
| Знать: как выполняется сложение и вычитание числовых неравенств Уметь: оценивать числовые неравенства
|
| ||||
| 5/70 | Умножение числовых неравенств |
|
| |||||||
| 6/71 | Подготовка к к/р по теме «Свойства числовых неравенств» |
| Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: определение числовых неравенств, свойства числовых неравенств, как выполняется сложение и вычитание числовых неравенств Уметь: применять свойства числовых неравенств при решении неравенств, иллюстрировать эти свойства на координатной прямой, оценивать числовые неравенства |
| ||||
| 7/72 | К/р №7 по теме: «Свойства числовых неравенств» | 1 | Проверка ЗУН |
|
|
| ||||
| 8/73 | Пересечение и объединение множеств | 1 | Познакомить с понятиями пересечение и объединение множеств | Круг Эйлера | Знать: понятия пересечение и объединение множеств Уметь: изображать пересечение и объединение множеств с помощью кругов Эйлера |
| ||||
| 9/74 | Числовые промежутки |
2 | Научить изображать неравенства в виде промежутков и записывать их обозначения | Числовой отрезок, интервал, полуинтервал, числовой луч, открытый числовой луч | Знать: обозначение и название числовых промежутков Уметь: изображать числовые промежутки на координатной прямой |
| ||||
| 10/75 | Изображение числовых промежутков на координатной прямой |
| ||||||||
| 11/76 | Линейное неравенство с одной переменной |
3 | Сформулировать свойства, которые используются при решении неравенств с одной переменной Дать определение линейного неравенства с одной переменной | Равносильные неравенства Линейное неравенство с одной переменной | Знать: определение линейного неравенства с одной переменной, свойства, которые используются при решении неравенств с одной переменной Уметь: решать линейные неравенства с одной переменной |
| ||||
| 12/77 | Решение неравенств с одной переменной | Сформировать умения решать линейные неравенства с одной переменной |
|
| ||||||
| 13/78 | Решение неравенств |
|
| |||||||
| 14/79 | Система неравенств с одной переменной |
4 | Дать определение понятия системы неравенств, научить решать системы неравенств. |
| Знать: определение системы неравенств Уметь: решать системы неравенств
|
| ||||
| 15/80 | Изображение решения системы неравенств на координатной прямой |
|
| |||||||
| 16/81 | Решение системы неравенств |
|
| |||||||
| 17/82 | Подготовка к к/р по теме «Решение линейных неравенств и их систем» | 1 | Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: обозначение и название числовых промежутков, определение линейного неравенства с одной переменной, свойства, которые используются при решении неравенств с одной переменной Уметь: изображать числовые промежутки на координатной прямой, решать линейные неравенства с одной переменной, решать системы неравенств |
| ||||
| 18/83 | К/р №8 по теме: «Решение линейных неравенств и их систем» | 1 | Проверка ЗУН |
|
|
| ||||
| Глава 5: СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ. ЭЛЕМЕНТЫ СТАТИСТИКИ. ( 11ч) |
| |||||||||
| 1/84 | Определение степени с целым показателем |
2 | Дать определение дроби с целым показателем, научить представлять степень с целым, отрицательным показателем в виде дроби и наоборот | а n = | Знать: определение степени с целым показателем Уметь: представлять степень с целым, отрицательным показателем в виде дроби и наоборот |
| ||||
| 2/85 | Степень с отрицательным показателем |
| ||||||||
| 3/86 | Свойства степени с целым показателем |
3 | Ознакомить учащихся со свойствами степени с целым показателем, выработать умения применять эти свойства | Таблица свойств степени с целым показателем | Знать: свойства степени с целым показателем Уметь: применять эти свойства |
| ||||
| 4/87 | Применение свойств к вычислению |
| ||||||||
| 5/88 | Представление степени в виде произведения |
| ||||||||
| 6/89 | Стандартный вид числа |
1
| Ознакомить учащихся с записью чисел в стандартном виде и с выполнением действий над числами, записанными в стандартном виде. | Стандартный вид числа | Знать: что значит запись числа в стандартном виде Уметь: записать число в стандартном виде и выполнять действия над числами, записанными в стандартном виде. |
| ||||
| 7/90 | Представление числа в стандартном виде |
| ||||||||
| 8/91 | Сбор и группировка статистических данных | 1 | Познакомить со сбором и группировкой статистических данных | Таблица частот, относительная частота, интервальный ряд, генеральная и выборочная совокупности | Знать: как производится сбор и группировка статистических данных Уметь: находить среднее арифметическое, размах и моду ряда данных |
| ||||
| 9/92 | Наглядное представление статистической информации |
1 | Построение столбчатых, круговых диаграмм, гистограмм, графиков статистических данных | гистограмма | Знать: как наглядно представляется статистическая информация Уметь: читать и строить диаграммы, гистограммы, графики статистических данных |
| ||||
| 10/93 | Повторение темы «Степень с целым показателем» | 1 | Обобщить и систематизировать знания по теме, подготовить к написанию контрольной работы |
| Знать: определение и свойства степени с целым показателем, что значит запись числа в стандартном виде Уметь: представлять степень с целым, отрицательным показателем в виде дроби и наоборот, записать число в стандартном виде и выполнять действия над числами, записанными в стандартном виде. |
| ||||
| 11/94 | К/р № 9 «Степень с целым показателем» | 1 | Проверка ЗУН |
|
|
| ||||
| ПОВТОРЕНИЕ (8ч) |
| |||||||||
| 1/95 | Повторение темы «Рациональные дроби» |
5 | Проверка и коррекция ЗУН, подготовка к итоговой контрольной работе |
| Знать все основные понятия курса Уметь применять полученные знания при решении заданий |
| ||||
| 2/96 3/97 | Повторение темы «Квадратные корни» и «Квадратные уравнения» |
|
| |||||||
| 4/98 | Повторение темы «Неравенства» |
|
| |||||||
| 5/99 | Повторение темы Степень с целым показателем» |
|
| |||||||
| 6/100 7/101 | Итоговая контрольная работа | 2 | Проверка ЗУН |
|
|
| ||||
| 8/102
| Урок-игра «По страницам занимательной алгебры» | 1 | Познакомить с некоторыми задачами и их решением из занимательной алгебры |
|
|
| ||||
ГЕОМЕТРИЯ
| № урока |
Тема урока | Кол-во часов |
Элементы содержания образования |
Основные понятия |
Знания, умения |
| Глава 5: ЧЕТЫРЁХУГОЛЬНИКИ (14ч) | |||||
| 1/1 | Понятие многоугольника. Выпуклый многоугольник. | 1 | Ввести понятие многоугольника, познакомить с его элементами, внешней и внутренней областью многоугольника | Многоугольник, выпуклый многоугольник | Знать, определение многоугольника и четырёхугольника и их элементов; понятие выпуклого многоугольника; утверждение о сумме углов выпуклого многоугольника Уметь изображать многоугольники и четырёхугольники, называть по рисунку их элементы: диагонали, вершины, стороны, соседние и противоположные вершины и стороны, применять полученные знания в ходе решения задач |
| 2/2 | Четырехугольник | 1 | Вывести формулу суммы углов выпуклого многоугольника, сумму углов четырехугольника |
| |
| 3/3 | Параллелограмм и его свойства |
3 | Дать определение параллелограмма, рассмотреть свойства о диагоналях параллелограмма, противоположных сторонах и углах | параллелограмм | Знать определение параллелограмма, формулировки свойств и признаков параллелограмма. уметь доказывать свойства и признаки параллелограмма и применять эти знания к решению задач |
| 4/4 | Признаки параллелограмма | Рассмотреть три признака параллелограмма |
| ||
| 5/5 | Решение задач по теме «Параллелограмм» | Закрепить в процессе решения задач, полученные ЗУН |
| ||
| 6/6 | Трапеция |
3 | Дать определение трапеции, познакомить с её элементами, дать определение равнобедренной и прямоугольной трапеции | Трапеция, основание трапеции, боковые стороны трапеции | Знать определение трапеции, её элементы, формулировку теоремы Фалеса Уметь строить трапеции, равнобедренные и прямоугольные трапеции, доказывать теорему Фалеса, применять полученные знания к решению задач |
| 7/7 | Теорема Фалеса | Доказать теорему Фалеса |
| ||
| 8/8 | Решение задач по теме «Трапеция» | Закрепить в процессе решения задач, полученные ЗУН |
| ||
| 9/9 | Прямоугольник |
4 | Дать понятие прямоугольника, рассмотреть свойство и доказать признак прямоугольника | прямоугольник | Знать определения прямоугольника, ромба, квадрата, формулировки их признаков и свойств; определения симметричных точек и фигур относительно прямой и точки Уметь строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией |
| 10/10 | Ромб, квадрат | Дать понятие ромба и квадрата, рассмотреть свойства ромба и квадрата
| Ромб, квадрат | ||
| 11/11 | Решение задач по теме «Прямоугольник, ромб, квадрат» | Закрепить в процессе решения задач, полученные ЗУН |
| ||
| 12/12 | Осевая и центральная симметрии | Ввести понятие симметрии | Симметрия, осевая и центральная симметрия | ||
| 13/13 | Подготовка к к/р по теме «Четырехугольники» | 1 | Закрепить в процессе решения задач, полученные ЗУН, подготовить учащихся к контрольной работе |
| Уметь применять полученные знания к решению задач |
| 14/14 | К/р №1 «Четырехугольники» | 1 | Проверка ЗУН |
|
|
| Глава 6: ПЛОЩАДЬ (14ч) | |||||
| 1/15 | Понятие площади многоугольника |
2 | Дать представление об измерении площадей многоугольников, рассмотреть основные свойства площадей и вывести формулы для вычисления площадей квадрата и прямоугольника | Формула площади квадрата и прямоугольника | Знать, основные свойства площадей и формулы для вычисления площади квадрата и прямоугольника Уметь использовать формулы и свойства площадей к решению задач |
| 2/16 | Площадь прямоугольника и квадрата | ||||
| 3/17 | Площадь параллелограмма | 6 | Опираясь на основные свойства площадей и теорему о площади прямоугольника, вывести формулы для вычисления площадей параллелограмма, треугольника и трапеции; рассмотреть теорему об отношении площадей треугольников, имеющих по равному углу | Формула площади параллелограмма | Знать, формулу площади паралле- лограмма Уметь, использовать формулу к решению задач |
| 4/18 | Решение задач на нахождение площади параллелограмма |
| |||
| 5/19 | Площадь треугольника | Формула площади треугольника | Знать формулу площади треугольника Уметь: использовать формулу к решению задач | ||
| 6/20 | Решение задач на нахождение площади треугольника |
| |||
| 7/21 | Площадь трапеции | Формула площади трапеции | Знать формул площади трапеции Уметь использовать формулу к решению задач | ||
| 8/22 | Решение задач на нахождение площади трапеции |
| |||
| 9/23 | Теорема Пифагора |
3 | Рассмотреть теорему Пифагора и показать ее применение в ходе решения задач | Теорема Пифагора | Знать теорему Пифагора и обратную ей теорему Уметь доказывать их и применять при решении задач |
| 10/24 | Теорема, обратная теореме Пифагора | Рассмотреть теорему, обратную теореме Пифагора показать ее применение в ходе решения задач | Теорема, обратная теореме Пифагора | ||
| 11/25 | Решение задач на применение теоремы Пифагора и обратной ей теоремы | Совершенствовать навыки решения задач на применение теоремы Пифагора и обратной ей теоремы |
| ||
| 12/26 | Зачет по теме: «Площадь» | 1 |
|
|
|
| 13/27 | Подготовка к к/р по теме: «Площадь» | 1 | Закрепить в процессе решения задач, полученные ЗУН, подготовить учащихся к контрольной работе |
| Уметь применять полученные знания к решению задач |
| 14/28 | К/р №2 по теме: «Площадь» | 1 | Проверка ЗУН |
|
|
| ПОДОБНЫЕ ТРЕУГОЛЬНИКИ(19 ЧАСОВ) | |||||
| 1/29 | Определение подобных треугольников |
2 | Ввести понятие пропорциональных отрезков и подобных треугольников; рассмотреть св-во биссектрисы треугольника | Отношение отрезков, пропорциональные отрезки, подобные треугольники, коэффициент подобия | Знать определение пропорциональных отрезков и подобных треугольников, теорему об отношении площадей подобных треугольников Уметь применять их при решении задач |
| 2/30 | Отношение площадей подобных треугольников | Рассмотреть теорему об отношении площадей подобных треугольников и показать ее применение в процессе решения задач |
| ||
| 3/31 | Первый признак подобия треугольников |
4 | Рассмотреть первый признак подобия треугольников и сформировать навыки применения этого признак при решении задач | Теорема, выражающая первый признак подобия треугольников | Знать признаки подобия треугольников Уметь их доказывать и применять при решении задач Знать утверждения, сформулированные в №556, №558 и уметь применять их при решении задач типа №557
|
| 4/32 | Решение задач на применение первого признака подобия треугольников | Сформировать навыки решения задач на применение первого признака подобия треугольников |
| ||
| 5/33 | Второй и третий признаки подобия треугольников | Рассмотреть второй и третий признака подобия и показать их применение при решении задач | Теоремы, выражающие второй и третий признаки подобия треугольников | ||
| 6/34 | Решение задач на применение признаков подобия | Сформировать навыки применения признаков при решении задач |
| ||
| 7/35 | Подготовка к к/р по теме: «Признаки подобия треугольников» |
1 | Закрепить в процессе решения задач, полученные ЗУН, подготовить учащихся к контрольной работе |
| Уметь применять полученные знания к решению задач |
| 8/36 | К/р №3 по теме: «Признаки подобия треугольников» | 1 | Проверка ЗУН |
|
|
| 9/37 | Средняя линия треугольника | 1 | Рассмотреть теорему о средней линии треугольника и показать ее применение в процессе решения задач | Средняя линия треугольника | Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника, пропорциональных отрезках в прямоугольном треугольнике Уметь их доказывать и применять при решении задач Уметь с помощью циркуля делить отрезок в данном отношении и решать задачи на построение типа №586-590 |
| 10/38 | Свойство медиан треугольника | 1 | Рассмотреть свойство медиан треугольника и показать его применение в процессе решения задач |
| |
| 11/39 | Пропорциональные отрезки | 1 | Ввести понятие среднего пропорционального двух отрезков; рассмотреть свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла | Среднее пропорциональное | |
| 12/40 | Пропорциональные отрезки в прямоугольном треугольнике | 1 | Совершенствовать навыки решения задач на применение теории подобных треугольников |
| |
| 13/41 | Измерительные работы на местности | 1 | Показать применение подобия треугольников в измерительных работах на местности |
| |
| 14/42 | Задачи на построение методом подобия | 1 | Выработать навыки использования теорем подобных треугольников при решении задач |
| |
| 15/43 | Решение задач на построение методом подобных треугольников |
1 | Совершенствовать навыки решения задач методом подобия |
| |
| 16/44 | Синус, косинус и тангенс острого угла прямоугольного треугольника |
2 | Ввести понятие синуса, косинуса, тангенса острого угла прямоугольного треугольника | Определение синуса, косинуса, тангенса острого угла прямоугольного треугольника, основное тригонометрическое тождество | Знать определение синуса, косинуса, тангенса острого угла прямоугольного треугольника Уметь доказывать основное тригонометрическое тождество Знать значения синуса, косинуса, тангенса углов 30º, 45°, 60º Уметь решать задачи типа №591-602 |
| 17/45 | Значения синуса, косинуса, тангенса углов 30º, 45°, 60º | Научить вычислять значения синуса, косинуса, тангенса углов 30º, 45°, 60º |
|
| |
| 18/46 | Подготовка к к/р по теме: «Применение подобия к решению задач», «Соотношения между сторонами и углами в прямоугольном треугольнике» |
1
| Закрепить в процессе решения задач, полученные ЗУН, подготовить учащихся к контрольной работе |
| Уметь применять полученные знания к решению задач |
| 19/47 | К/р/ №4 по теме: «Применение подобия к решению задач», «Соотношения между сторонами и углами в прямоугольном треугольнике» |
1 | Проверка ЗУН |
|
|
| Окружность (17 часов) | |||||
| 1/48 | Взаимное расположение прямой и окружности | 1 | Рассмотреть различные случаи взаимного расположения прямой и окружности | Касательная к окружности, точка касания, отрезки касательных, проведенные из одной точки | Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной Уметь:доказывать свойство и признак касательной и применять их при решении задач типа №631, 633-636, 638-643, 648 |
| 2/49 | Касательная к окружности | 1 | Рассмотреть свойство касательной и ее признак; показать их применение при решении задач |
| |
| 3/50 | Решение задач по теме «Касательная к окружности» | 1 | Совершенствовать навыки решения задач по теме |
| |
| 4/51 | Градусная мера дуги окружности | 1 | Ввести понятие градусной меры дуги окружности, центрального угла | Полуокружность, центральный угол. | Знать определение центрального и вписанного углов; как определяется градусная мера дуги окружности; теорему о вписанном угле, следствия из нее, теорему о произведении отрезков пересекающихся хорд Уметь доказывать эти теоремы и применять при решении задач типа № 651-657, 659, 666-669 |
| 5/52 | Теорема о вписанном угле | 1 | Ввести понятие вписанного угла, рассмотреть теорему о вписанном угле и следствия из нее | Вписанный угол | |
| 6/53 | Теорема об отрезках пересекающихся хорд | 1 | Рассмотреть теорему об отрезках пересекающихся хорд, показать ее применение при решении задач |
| |
| 7/54 | Решение задач по теме: «Центральные и вписанные углы» | 1 | Систематизировать теоретические знания и совершенствовать навыки решения задач |
| |
| 8/55 | Свойство биссектрисы угла | 1 | Рассмотреть свойство биссектрисы угла и показать его применение при решении задач |
| Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия; теорему о пересечении высот треугольника Уметь доказывать эти теоремы и применять их при решении задач типа №674-679, 682-686 |
| 9/56 | Серединный перпендикуляр | 1 | Рассмотреть теорему о серединном перпендикуляре и показать ее применение при решении задач | Серединный перпендикуляр к отрезку | |
| 10/57 | Теорема о точке пересечения высот треугольника | 1 | Рассмотреть теорему о точке пересечения высот треугольника и показать ее применение при решении задач |
| |
| 11/58 | Вписанная окружность | 1 | Ввести понятие вписанной и описанной окружностей; рассмотреть теорему об окружности, вписанной в треугольник | Вписанная окружность, описанная окружность | Знать какая окружность называется вписанной в многоугольник и какая описанной около многоугольника, теоремы об окружности, вписанной в треугольник, и об окружности описанной около треугольника, свойства вписанного и описанного четырехугольников Уметь их доказывать и применять при решении задач типа №689-696, 701-707, 709-711 Знать утверждения задач №724, 729 и уметь их применять при решении задач типа №698-700, 708 |
| 12/59 | Свойство вписанного четырехугольника | 1 | Рассмотреть свойство вписанного четырехугольника и показать его применение при решении задач |
| |
| 13/60 | Описанная окружность | 1 | Ввести понятия описанной около многоугольника окружности и вписанного в окружность многоугольника; рассмотреть теорему об окружности, описанной около треугольника и показать ее применение при решении задач | описанная около многоугольника окружность и вписанный в окружность многоугольник | |
| 14/61 | Свойство вписанного четырехугольника | 1 | Рассмотреть свойство вписанного четырехугольника и показать его применение при решении задач |
| |
| 15/62 16/63 | Решение задач по теме: «Окружность» | 2 | Систематизировать теоретические знания и совершенствовать навыки решения задач по теме: «Окружность» |
|
|
| 17/64 | К/Р №5 по теме: «Окружность» | 1 | Проверка ЗУН |
|
|
| ИТОГОВОЕ ПОВТОРЕНИЕ (4 ЧАСА) | |||||
| 1/65 | Повторение по теме: «Четырехугольники», «Площадь» | 1 |
|
| Знать: формулировки определений, свойств, признаков: параллело-грамма, ромба, трапеции; формулы для вычисления площадей треугольника, параллелограмма, ромба, трапеции, квадрата, прямоугольника; теорему Пифагора Уметь: находить элементы четырехугольников, опираясь на изученные свойства, выполнять чертеж по условию задачи; вычислять площадь четырехугольника. |
| 2/66 | Повторение по теме: «Подобные треугольники», «Окружность» | 1 |
|
| Знать определение подобных треугольников, признаки подобия треугольников,определения синуса, косинуса, тангенса; значения тригонометрических функция для углов 30º, 45°, 60º Уметь применять признаки подобия к доказательству теорем и решению задач; применять метод подобия при решении задач на построение
|
| 3/67 | Урок занимательной геометрии | 1 |
|
|
|
| 4/68 | Урок-игра «Аукцион знаний» | 1 |
|
|
|
| ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВ С ЗПР Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания. В результате изучения математики ученик должен знать/понимать
Арифметика/уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Алгебра/уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Элементы логики, комбинаторики, статистики и теории вероятностейуметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Геометрия/уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
|
КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ УЧАЩИХСЯ
ВИДЫ И ФОРМЫ КОНТРОЛЯ
Контроль знаний, умений и навыков учащихся - важнейший этап учебного процесса, выполняющий обучающую, проверочную, воспитательную и корректирующую функции. В структуре программы проверочные средства находятся в логической связи с содержанием учебного материала. Реализация механизма оценки уровня обученности предполагает систематизацию и обобщение знаний, закрепление умений и навыков; проверку уровня усвоения знаний и овладения умениями и навыками, заданными как планируемые результаты обучения. Они представляются в виде требований к подготовке учащихся.
Для контроля уровня достижений учащихся используются такие виды контроля как: входной, текущий, тематический, итоговый контроль. Формы контроля: контрольные работы, самостоятельные работы, зачеты, математические диктанты, графические диктанты.
Для текущего тематического контроля и оценки знаний в системе уроков предусмотрены уроки-зачеты, контрольные работы. Курс завершают уроки, позволяющие обобщить и систематизировать знания, а также применить умения и навыки на практике.
При организации учебно-познавательной деятельности предполагается работа с дидактическим раздаточным материалом, где имеются вопросы и задания, в том числе в форме самостоятельных и проверочных работ, познавательных задач, карточках-заданиях, в творческих заданиях (рисунок, кроссворд).
Все эти задания выполняются как по ходу урока, так и даются на домашнее задание.
По окончании четверти, а так же по окончании курса проводится итоговая контрольная работа.
СИСТЕМА ОЦЕНИВАНИЯ УСТНЫХ И ПИСЬМЕННЫХ РАБОТ ПО МАТЕМАТИКЕ
Ответ оценивается оценкой «5», если ученик:
полностью раскрыл содержание материала в объеме, предусмотренном программой и учебником, изложил материал грамотным языком, точно используя математические термины и символику в определенной последовательности, правильно выполнил рисунки и чертежи, графики, соответствующие ответу, показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания, отвечал самостоятельно без наводящих вопросов, возможны одна - две неточности при освещении второстепенных вопросов или в высказываниях, которые ученик легко исправил после замечания учителя.
2. Ответ оценивается оценкой «4», если ответ удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков: в изложении допущены небольшие пробелы, не исказившие математического содержания ответа; допущены одна – две неточности при освещении основного содержания ответа, исправленные после замечания учителя; допущена ошибка, один или не более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
3.Оценка «3» ставится в следующих случаях:
неполно раскрыто содержание материала, имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленных после наводящих вопросов учителя; ученик не справился с применением теории в новой ситуации при выполнении задания, но выполнил задания обязательного минимума содержания по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
4. Отметка «2» ставится в следующем случае:
не раскрыто основное содержание учебного материала; допущены ошибки в определении понятий, при использовании математической терминологии; обнаружено незнание и непонимание учеником большей или наиболее важной части учебного материала.
5. Отметка «1» ставится, если учащийся обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изучаемому материалу.
СИСТЕМА ОЦЕНИВАНИЯ КОНТРОЛЬНЫХ РАБОТ
Включает в себя проверку достижения каждым обучающимся как уровня обязательной математической подготовки, так и проверку повышенного уровня знаний. Выделение в контроле двух принципиальных этапов, с одной стороны дает возможность получать объективную информацию о состоянии знаний и умений учащихся, с другой стороны, обеспечивает возможность ученикам с разным уровнем подготовки продемонстрировать свои достижения. Наличие в контрольных работах заданий под знаком «*» дает возможность продемонстрировать свои способности тем учащимся, которые имеют углубленный уровень знаний по математике.
Оценка «3» ставится за правильное выполнение заданий, отмеченных знаком «о».
Оценка «4» ставится за правильное выполнение заданий, отмеченных знаком «о», и верно выполненное задание повышенного уровня сложности.
Оценка «5» ставится за все верно выполненные задания, без учета заданий, отмеченных знаком «*».
Если ученик справился с заданием под знаком «*», то ему выставляется вторая оценка «5».
СИСТЕМА ОЦЕНИВАНИЯ ЗАЧЕТНЫХ РАБОТ
В конце изучения каждого модуля проводится зачетная работа, которая состоит из двух частей: теоретической и практической. Если ученик сдает теоретическую часть, то ему может быть выставлена оценка «3». Практическая часть имеет дифференцированные задания, начиная с уровня обязательной подготовки и заканчивая углубленным уровнем. В зависимости от выполненного объема практической части и при успешной сдачи теоретического зачета, ученику выставляется оценка «4» или «5».
Система оценивания для детей с ЗПР ничем не отличается от системы оценивания приведённой выше, поэтому похвала и поощрение - это тоже большая движущая сила в обучении детей данной категории. Важно, чтобы ребенок поверил в свои силы, испытал радость от успеха в учении.
Учебно – методическое обеспечение:
Учебник: Алгебра 8./Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Пешков/ М.: Просвещение, 2009г.
Дидактический материал по алгебре 8класс/В.И.Жохов, Ю.Н.Макарычев, Н.Г.Миндюк/ М.: Просвещение, 2009г
Поурочные разработки по алгебре к учебнику Ю.Н.Макарычева и др.8 класс – М.: ВАКО, 2008г.
Проверочные работы с элементами тестирования по алгебре 8 класс – Саратов: «Лицей»,2002г.
Алгебра. Тесты для промежуточной аттестации.7-8 класс. Под редакцией Ф.Ф.Лысенко.Ростов-на-Дону: Легион,2008г.
Алгебра.8 класс: самостоятельные и контрольные работы/авт.-сост. О.Л.Безрукова. – Волгоград: Учитель, 2007
Учебник: Геометрия, 7-9.Л. С.Атанасян, В.Ф.Бутузов, С.В.Кадомцев и др. М.: Просвещение, 2003.
Зив Б.Г. Дидактические материалы по геометрии для 8 кл.-М.: Просвещение, 2005
Изучение геометрии в 7-9 классах, методические рекомендации к учеб.: Книга для учителя /Л.С.Атанасян, В.Ф.Бутузов, - М.: Просвещение, 2003.
Поурочные разработки по учебнику Атанасяна Л.С., Н.Ф.Гаврилова.Москва «Вако» 2008.
Похожие файлы
object(ArrayObject)#853 (1) {
["storage":"ArrayObject":private] => array(6) {
["title"] => string(264) "Адаптированная рабочая коррекционно-образовательная программа по математике для детей младшего школьного возраста с ЗПР и ОВЗ 2 класс (VII вид) "
["seo_title"] => string(159) "adaptirovannaia-rabochaia-korriektsionno-obrazovatiel-naia-proghramma-po-matiematikie-dlia-dietiei-mladshiegho-shkol-nogho-vozrasta-s-zpr-i-ovz-2-klass-vii-vid"
["file_id"] => string(6) "231239"
["category_seo"] => string(10) "matematika"
["subcategory_seo"] => string(12) "planirovanie"
["date"] => string(10) "1442423028"
}
}
Подтверждение авторства
Пожалуйста, введите ваш Email.
Если вы хотите увидеть все свои работы, то вам необходимо войти или зарегистрироваться
Полезное для учителя
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
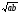 =
= 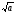 ∙
∙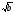
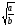 =
= 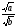
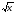 2 = │х │
2 = │х │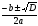
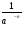 , а ≠ 0
, а ≠ 0















