Проект по математике "Знакомство с пропорцией"

Данный проект посвящен теме курса математики 6-го класса «Пропорции». Цель данного проекта – исследовать применение пропорций в области математики, живописи, архитектуры, медицины. Задания и теоретический материал, предлагаемый учащимся в ходе реализации проекта, поможет им овладеть кругом практически важных понятий и умений, связанных с пропорциональностью величин и приобрести новые знания в области понятия отношения и пропорции с точки зрения «Золотого сечения». Важным результатом проекта является понимание учащимися простоты, красоты пропорций, их важности для правильного и гармоничного изображения предмета.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Юрченко Л.Р.-сценарий»

Знакомство с пропорцией или секрет розы.
Фамилия, имя отчество			Юрченко Лариса Рустановна
Регион			Ленинградская область
Населенный пункт, в котором находится школа/ОУ			г. Тихвин
Номер и/или название школы/ОУ			МОУ «СОШ 9»
Описание проекта
Название темы вашего учебного проекта
Знакомство с пропорцией или секрет розы.
Краткое содержание проекта
Данный проект посвящен теме курса математики 6-го класса «Пропорции». Цель данного проекта – исследовать применение пропорций в области математики, живописи, архитектуры, медицины. Задания и теоретический материал, предлагаемый учащимся в ходе реализации проекта, поможет им овладеть кругом практически важных понятий и умений, связанных с пропорциональностью величин и приобрести новые знания в области понятия отношения и пропорции с точки зрения «Золотого сечения». Важным результатом проекта является понимание учащимися простоты, красоты пропорций, их важности для правильного и гармоничного изображения предмета.
Предмет(ы)
Математика
Класс(-ы)
6 класс общеобразовательной школы, базовый уровень
Приблизительная продолжительность проекта
4 урока
Основа проекта
Образовательные стандарты
В результате реализации данного проекта предполагается формирование умений, необходимых обучающимся в условиях реализации ФГОС второго поколения: личная ответственность и гибкость в различных ситуациях, способность к саморазвитию, применению новых идей и доведению их до других людей, умения работать с информацией и медиасредствами- находить, анализировать, управлять, оценивать, создавать информацию, способность работать в команде, продуктивно работать в коллективе прочно усвоить свойство пропорции, так как оно найдёт применение на уроках математики, химии, физики. Предполагается, что практическим результатом станет презентация данного проекта, презентация групп: учёные, медики и биологи, архитекторы. Продолжительность проекта 4 урока учебного времени, остальное внеурочное время.
Планируемые результаты обучения
После завершения проекта учащиеся приобретут следующие умения: - личностные: 1) умение ясно, точно, грамотно, излагать свои мысли в устной и письменной речи, понимать смысл, выстраивать аргументации, приводить примеры и контрпримеры; представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации; 3) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений. - метапредметные: 1) первоначальное представление об идеях и методах математики, как об универсальном языке науки и техники, о средстве моделирования явлений и процессов; 2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; 3) понимание сущности алгоритмических предписаний и умений действовать в соответствии с предложенным алгоритмом. - предметные: овладение практически значимыми математическими умениями навыками, их применение к решению математических и нематематических задач, предполагающее умение: 1) пользоваться математическими формулами и самостоятельно составлять формулы зависимости между величинами на основе обобщения частных случаев и обобщения; 2) применять изученное понятие, результаты и методы при решении задач из различных разделов курсов в том числе задач не сводящихся к непосредственному применению известных алгоритмов.
Вопросы, направляющие проект
Основополагающий вопрос		Пропорция: математический объект или основа красоты в жизни? Какую роль пропорция играет в нашей жизни?
Проблемные вопросы учебной темы		1.«Дайте мне точку опоры и я переверну Землю.» Архимед. 2. «А что есть красота?» Н. Заболоцкий. 3. Где ты, пропорция? И как тебя найти? 4. Математическая сущность золотого сечения? 5. Значение золотого сечения в различных науках? 6. Значение пропорции в жизни человека? 7. Где можно использовать знания о пропорциональных величинах?
Учебные вопросы		Что показывает отношение двух чисел? Что такое пропорция? В чём состоит основное свойство пропорции? Что такое пропорциональность? Что называют «Золотой пропорцией» или «золотым сечением»?
План оценивания
График оценивания
До работы над проектом	Ученики работают над проектом и выполняют задания			После завершения работы над проектом
Составить план проведения проекта Вводная презентация учителя. Список тем для исследований Анкетирование Создание таблиц З-И-У Формирование групп Критерии оценивания презентации. Правила работы в группах	1. Практическая работа по учебному плану 2. «Маршрутные листы – задания группам» 3. Критерии самооценки работы в группах 4. Неформальное общение с учащимися во внеурочное время. 5. Оценочные листы 6. Обсуждение промежуточных результатов деятельности 7. Таблицы З - И – У 8. Фотоотчёт			критерии оценивания работ: защита презентаций взаимное обсуждение творческих работ интервью Таблицы З - И - У
Критерии	Показатели			Индикатор
				да	нет
Структура	1. Содержи титульный лист, название. 2. Содержание разделов выдержано в логической последовательности. 3. Указаны информационные ресурсы. 4. Сделаны выводы. 5. Логическая последовательность информации на слайдах. 6. Информация хорошо структурирована, изложена ясно и последовательно.
Содержание	1. Содержание презентации соответствует заявленному названию. 2. Презентация даёт ответы на основополагающие и проблемные вопросы. 3. Для исследования использовано более одного источника. 4. Информация презентации полезна (интересна) для читателей. 5. Презентация является результатом коллективных усилий. 6. Сформулирована цель, гипотеза.
Оформление	1. Оформление продуманно, выдержано в едином стиле. 2. Оформление подчёркивает структуру статьи (наличие заголовков разного уровня, выделение шрифта и т.п.). 3. Изображение иллюстрируют содержание, подчёркивают го, делают более понятным.
Грамотность	1. Текст не содержит ошибок. 2. Логика изложения (правильная речь)
Описание методов оценивания
На подготовительном этапе работы над проектом использую методы, позволяющие активизировать работу и внимание учеников: выявление уровня сформированности УУД по теме «Пропорции» мозговой штурм: ученики продумывают темы и идеи, связанные с заданной темой и связывают эти идеи с предварительными знаниями и новыми возможностями. Работа над проектом начинается с оценивания имеющихся у учеников знаний по теме проекта. Проводится входной контроль, который позволяет выявить основные знания по теме «Отношения и пропорции» В ходе беседы в процессе просмотра стартовой презентации учителя; проводится анкетирование по вопросам таблицы З–И–У («Знаю – Интересуюсь – Учусь»). Ученики знакомятся с предлагаемыми темами исследований, соответствующими стандартным требованиям учебной программы, распределяются по группам, планируют ход исследований, знакомятся с критериями итоговых работ. Итоговое оценивание направлено, в первую очередь, на умения соотносить проблемные вопросы с целями исследований, аргументацию выводов, рассказать об организации взаимодействия учеников в группе, показать уровень успешности каждого ученика. Каждая группа в результате представляет свою исследовательскую работу по выбранному направлению.
Сведения о проекте
Необходимые начальные знания, умения, навыки
Учащиеся должны знать:  понятие отношения двух чисел;  что показывает отношение двух чисел. Учащиеся должны уметь:  правильно представлять частное в виде дроби (a:b=a/b) и переходит от одной записи к другой; Учащиеся должны обладать навыками:  уверенного выполнения арифметических действий. Свободно владеть математической терминологией оп данной теме; владеть программными знаниями по математике; иметь общие сведения о проекте; иметь навыки работы с различными информационными источниками. Концептуальные знания и технические навыки, необходимые учащимся, чтобы начать выполнение этого проекта
Учебные мероприятия
Перед началом проекта учитель готовит все необходимые дидактические материалы, объясняет смысл изменения и проведения учебных занятий. Осуществляет подбор материала с использованием Интернет, размещает ссылки на найденные материалы на сайте Бобр Добр. Учит детей пользоваться закладками на этом сайте. Постановка задачи (1 урок) Ученики уже знают понятие отношения и пропорции и умеют находить отношения различных видов: обыкновенные дроби, десятичные дроби, целые числа. С помощью стартовой презентации и входного контроля учитель выясняет имеющиеся знания по этой теме. Определяются темы для исследований, класс разбивается на 4 группы, каждая из которых будет исследовать свою тему: 1 группа ( «Архитекторы») – работает по вычислению отношений по зданию Парфенона ; 2 группа («Художники») – работает по вычислению отношений по картине Шишкина «Сосновая роща»; 3 группа («Медики») - работает по вычислению отношений в теле человека; 4 группа («Биологи») – работает по вычислению отношений по предлагаемому растению. Исследования учащихся (2 урока) В течение следующих уроков ученики, при поддержке учителя, пытаются ответить на вопросы своей темы. Знакомятся с историческими сведениями. По результатам своей работы учащиеся создают материалы, в которых отражается результат их деятельности (Вики-статья, презентация, иллюстрации). Делают выводы по теме. В поддержку знаний и умений, которыми должен обладать ученик 21 века, учитель обеспечивает группы ресурсами, необходимыми для самооценки и отслеживания продвижения работы групп по этапам исследования, предлагает дидактические задания по теме проекта. Также учитель может предложить учащимся ссылки на Интернет-ресурсы проекта на сервисе хранения закладок Бобр Добр. Проводится совместное обсуждение, а затем оформление результатов работы группы. Защита проекта (1 урок) Каждая группа выступает с презентацией результатов, демонстрируя свои работы в форме презентации, вики-статьи. В завершении коллективно обсуждаются выводы, служащие ответом на основополагающий вопрос проекта. Учащиеся оценивают выступления групп в соответствии с критериями оценивания работы групп. Подводятся итоги, определяется группа, выполнившая самое полное и аргументированное исследование, осуществляется индивидуальная рефлексия. Проводится рефлексия в форме анкеты. Занятие №1 – ознакомительное, знакомство с темами и требованиями проекта, формирование творческих групп. Занятия №2-3 + внеурочное время – работа над проектом. Занятие №4 – защита проекта, рефлексия. Четкое описание учебного цикла — объем и последовательность учебных заданий и описание деталей выполнения учащимися планирования своего обучения
Материалы для дифференцированного обучения
Ученик с проблемами усвоения учебного материала (Проблемный ученик)		В работе над проектом ученики выполняют доступные для себя задания, четко определенные задачи на основе продуманного алгоритма действий. Они имеют возможность воспользоваться помощью других участников группы, проконсультироваться с учителем. Такие ученики должны почувствовать свою значимость в общем деле, почувствовать, что они могут быть успешными. В помощь таким ученикам предлагаются опорные карты, дополнительные схемы и справочный материал
Ученик, для которого язык преподавания не родной		Таких нет
Одаренный ученик
Материалы и ресурсы, необходимые для проекта
Технологии – оборудование (отметьте нужные пункты)
Фотоаппарат, лазерный диск, компьютер, принтер, видеокамера, цифровая камера, проекционная система, сканер.
Технологии – программное обеспечение (отметьте нужные пункты)
СУБД/электронные таблицы, программы обработки изображений, программы разработки веб-сайтов, настольная издательская система, веб-браузер, текстовые редакторы, программы электронной почты, мультимедийные системы, другие справочники на CD-ROM
Материалы на печатной основе		Ковалев Ф.В. Золотое сечение в живописи. К.: Выща школа, 1989. 2. Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983. 3. Стахов А., Слученкова А. Щербаков И. Код да Винчи и ряды Фибоначчи. - СПб.: Питер, 2006. 4. Петрович.Д. Теоретики пропорций: М.: Стройиздат, 1979. 5. Волошинов А.В. Математика и искусство
Другие принадлежности		Защита проектов происходит в рамках недели защиты проектов, приглашаются члены школьного научного общества.
Интернет-ресурсы		Бендукидзе А., Золотое сечение http://kvant.mirror1.mccme.ru/1973/08/zolotoe_sechenie.htm Бердукидзе А.Д. Золотое сечение http://kvant.mirror1.mccme.ru/1973/08/zolotoe_sechenie.htm Горелышева С. Е. Золотое сечение http://pages.marsu.ru/iac/resurs/gorelysheva/8.html Золотое сечение. Урок ведет математик Лазарь Людмила Павловна. http://rustimes.com/blog/post_1177437753.html Лаврус В.С. Золотое сечение. http://n-t.ru/tp/iz/zs.htm Радзюкевич А. В. Красивая сказка о “золотом сечении”. http://www.sibdesign.ru/index.php?text=1&razdel=stat&textnew=20030615041954 Радзюкевич А.В. Глава из книги "Законы красоты - мифология или технология?" http://www.a3d.ru/architecture/stat/17 Слайд РРТ. Башатьян Вера http://rrc.dgu.ru/res/crow.academy.ru/dm/lectures_/lect_08_/sem_08_/goldsection_/basharatian_/sld008.htm Титова Елена. Золотое Сечение http://goldsech.narod.ru/ Щетников А.И. Золотое сечение в «древней» и в «новой» эстетике. http://www.a3d.ru/architecture/stat/207 Энциклопедия замечательных людей. Золотое сечение http://www.abc-people.com/data/leonardov/zolot_sech-txt.htm
Другие ресурсы		Проведён эксперемен. Приглашены учащиеся 5 и 8 классов.

Просмотр содержимого документа
«ЮрченкоЛР-Анкета»

Фамилия, имя

В какой группе ты хотел бы работать?

Учёные
Архитекторы
Медики и биологи

Если в группе возникнет спорная ситуация, как ты поступишь?

Обращусь за помощью к родителям
Обращусь за помощью к друзьям
Посоветуюсь с учителем
Соберусь и справлюсь сам

Чем бы ты хотел заниматься в группе?

Руководить
Искать информацию
Оформлять результаты
Проводить эксперимент

Фамилия, имя

В какой группе ты хотел бы работать?

Учёные
Архитекторы
Медики и биологи

Если в группе возникнет спорная ситуация, как ты поступишь?

Обращусь за помощью к родителям
Обращусь за помощью к друзьям
Посоветуюсь с учителем
Соберусь и справлюсь сам

Чем бы ты хотел заниматься в группе?

Руководить
Искать информацию
Оформлять результаты
Проводить эксперимент

Фамилия, имя

В какой группе ты хотел бы работать?

Учёные
Архитекторы
Медики и биологи

Если в группе возникнет спорная ситуация, как ты поступишь?

Обращусь за помощью к родителям
Обращусь за помощью к друзьям
Посоветуюсь с учителем
Соберусь и справлюсь сам

Чем бы ты хотел заниматься в группе?

Руководить
Искать информацию
Оформлять результаты
Проводить эксперимент

Просмотр содержимого документа
«ЮрченкоЛР-Задания_группам»

В ходе работы над проектом мы постараемся ответить на вопрос:
«Поддаётя ли красота математическому описанию?

Группа Учёные

Перед Вами стоит задача:

выяснить, где возникло учение о пропорциях;
как оно развивалось;
как применяются пропорции в искусстве, географии, математике;
выяснить, что есть «божественная пропорция» и показать ее применение в различных областях.
Раскройте смысл метафоры «божественная красота».
Подберите рисунки, фотографии, картинки.

В ходе работы над проектом мы постараемся ответить на вопрос:
«Поддаётя ли красота математическому описанию?

Группа Архитекторы

Созданные произведения руками человека либо привлекают внимание на столетия, либо не привлекают внимания. Постарайтесь найти такие сооружения, которые привлекают внимание уже не одно столетие, также, которые не привлекают внимания.
Исследуйте кабинет Б-13 на предмет актуальности дизайна стен. Составьте план оформления стен кабинета с учётом законов пропорции.
Найти конкретные примеры связи красоты и пропорции.
Подберите рисунки, фотографии, картинки.

В ходе работы над проектом мы постараемся ответить на вопрос:
«Поддаётя ли красота математическому описанию?

Группа Медики и биологи

В своих трудах Вы должны отразить только те явления природы, растения и животные существа, в строении которых прослеживается золотое сечение как гармоническая пропорция.
Почему яйцо является символом Золотого сечения?
«Золотое сечение» повсеместно присутствует в теле человека. Оно стало для человека эталоном красоты. Исследуйте модели куклы, статуэтки, мягкой игрушки.
Исследуйте ветку дерева.
Подберите рисунки, фотографии, картинки.

В ходе работы над проектом мы постараемся ответить на вопрос:
«Поддаётя ли красота математическому описанию?

Группа Медики и биологи

В своих трудах Вы должны отразить только те явления природы, растения и животные существа, в строении которых прослеживается золотое сечение как гармоническая пропорция.
Почему яйцо является символом Золотого сечения?
«Золотое сечение» повсеместно присутствует в теле человека. Оно стало для человека эталоном красоты. Исследуйте модели куклы, статуэтки, мягкой игрушки.
Исследуйте ветку дерева.
Подберите рисунки, фотографии, картинки.

Просмотр содержимого презентации
«ЮрченкоЛР-Презентация учителя»

Гармония пропорций в природе, математике и искусстве Иоганн Kеплер говорил, что геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем. Теорему Пифагора знает каждый школьник, а что такое золотое сечение- далеко не все.

В ходе работы над проектом мы постараемся ответить на вопрос: «Поддаётя ли красота математическому описанию?»

Основопологающий вопрос

Пропорция: математический объект или основа красоты в жизни?

Проблемные вопросы

1. «Дайте мне точку опоры и я переверну Землю.» Архимед. 2. «А что есть красота?» Н. Заболоцкий. 3. Где ты, пропорция? И как тебя найти?

Учебные вопросы

Что показывает отношение двух чисел?
Что такое пропорция?
В чём состоит основное свойство пропорции?
Что такое пропорциональность?
Что называют «Золотой пропорцией» или «золотым сечением»?

Исследовать эти вопросы будут: Учёные Архитекторы Медики

Группа Учёные

Перед Вами стоит задача:

выяснить, где возникло учение о пропорциях;
как оно развивалось;
как применяются пропорции в литературе, музыке, физике, географии, биологии , математике ;
выяснить, что есть «божественная пропорция» и показать ее применение в различных областях.

Группа Архитекторы

Созданные произведения руками человека либо привлекают внимание на столетия, либо не привлекают внимания. Постарайтесь найти такие сооружения, которые привлекают внимание уже не одно столетие.

Группа Медики и биологи

В своих трудах Вы должны отразить только те явления природы, растения и животные существа, в строении которых прослеживается золотое сечение как гармоническая пропорция. Почему яйцо является символом Золотого сечения?

«Золотое сечение» повсеместно присутствует в теле человека. Оно стало для человека эталоном красоты. Найдите «золотые пропорции» в теле человека.

Ничто не нравится, кроме красоты, в красоте – ничто, кроме форм, в формах – ничто, кроме пропорций, в пропорциях – ничто, кроме числа.

Желаю удачи и терпения в ваших исследованиях !

Просмотр содержимого презентации
«ЮрченкоЛР»

Что общего между человеческим телом, цикорием, древнеегипетскими пирамидами и картиной Леонардо да Винчи? Ответ на этот вопрос таится в разгадке тайны Золотой пропорции. Проявленный мир настолько подчинен гармонии Золотой пропорции и пронизан числами ряда Фибоначчи, что порой кажется: только ими наша удивительная Вселенная и может быть объяснена.

Учитель МОУ СОШ № 9 г. Тихвин Юрченко Лариса Рустановна,

Пропорция: математический объект или основа красоты в жизни

Группа Учёные:

Вильховецкий Евгений

Мясникова Наталья

Скобелева Ангелина

Павлова Анастасия

Гипотеза.

Наше восприятие красоты основаны на математических законах

Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете - посередине? Или, может быть, с самого края?

Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная... Садясь на скамейку, вы произвели «золотое сечение».

В мире существует уникальная пропорция, которую называют «формулой красоты».

Понятие «золотое сечение» ввёл Леонардо да Винчи.

« Геометрия владеет двумя сокровищами – теоремой Пифагора и «Золотым сечением», и если первое и них можно сравнить с мерой золота, то второе – с драгоценным камнем»

Иоанн Кеплер

Золотое сечение – это деление отрезка, при котором длина его большей части так относится к длине меньшей части, как длина всего отрезка относится к длине большей части.

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.

Пифагор (580-500 г.г.до н.э.)

Проблему гармонии на Земле и во Вселенной принято считать вечной. Древние мыслители сводили цель науки к поиску объективной гармонии. В понятие гармонии Пифагор (580-500 гг. до нашей эры) включали симметрию и отношения целого и его частей - "золотое сечение"

Пирамида Хеопса

Сфинкс, охраняющий гробницу Тутанхамона

Французский архитектор Ле Корбюзье нашел,

что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамсеса, пропорции фигур соответствуют величинам золотого деления.

Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

В Фасаде Парфенона присутствуют злотые пропорции. При раскопках этого древнегреческого храма обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле также заложены пропорции золотого сечения .

В дошедшей до нас античной литературе золотое деление впервые упоминается в "Началах" Евклида. Во 2-й книге "Начал" дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др.. В средневековой Европе с золотым делением познакомились по арабским переводам "Начал" Евклида.

Основные вехи

VI век до н.э. Полагают, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

III век до н. э. впервые встречается в "Началах" Евклида

Конец 15 - нач. 16 веков Леонардо да Винчи ввёл термин "ЗОЛОТОЕ СЕЧЕНИЕ". В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи.

В 1900-х годах американский математик Марк Барр (Mark Barr) использовал греческую букву Фи (phi) для определения золотой пропорции

Чи́сла Фибона́ччи — элементы числовой последовательности

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 …

в которой каждое последующее число равно сумме двух предыдущих чисел.

Название по имени средневекового математика Леонардо Пизанского (или Фибоначчи)

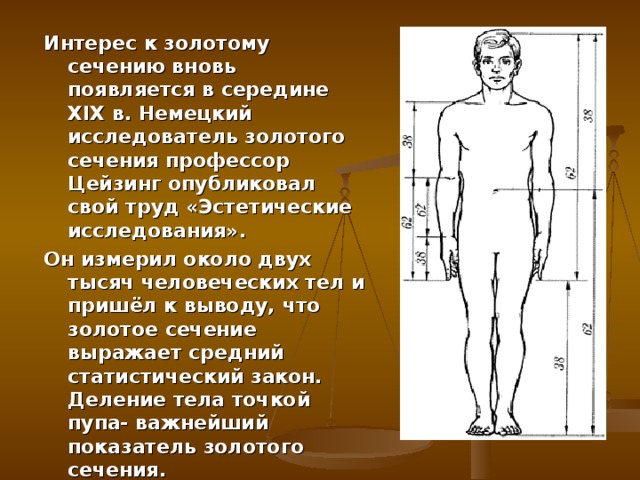
Интерес к золотому сечению вновь появляется в середине XI Х в. Немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования».

Он измерил около двух тысяч человеческих тел и пришёл к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа- важнейший показатель золотого сечения.

Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618 .

Расстояние от уровня плеча до макушки головы и размера головы равно 1:1.61Расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618Расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618Расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618 Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.

Это интересно . . .

Особенно хорошо удовлетворяет этой пропорции мужская фигура, и художники давно знают, что вопреки общему мнению, мужчины сложены красивее, чем женщины. У женщин наблюдается отклонение от норм золотого сечения, а обувь на высоком каблуке «восстанавливает» пропорцию и принцип золотого сечения торжествует. Именно поэтому высокий каблук почти всегда входит в состав женского костюма

Мы провели ПРАКТИЧЕСКОЕ ЗАДАНИЕ. Нашли на руке или на лице размеры, соответствующие золотому сечению.

ПРОВЕРЬТЕ:

1. Каждый палец нашей руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).

2. Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.

Пентаграмма – тайный знак пифагорейского братства – была выбрана ими в качестве символа жизни и здоровья.

Согласно легенде , один пифагореец заболел на чужбине и не мог перед смертью расплатиться с ухаживающим за ним хозяином дома. Последний нарисовал на стене своего дома звёздчатый пятиугольник. Увидав через несколько лет этот знак, другой странствующий пифагореец осведомился о случившимся у хозяина и щедро его вознаградил.

Пентаграмму изображали для того, чтобы спастись от проникновения в дом злых духов.

Отрывок из «Фауста»:

М е ф и с т о ф е л ь

Трудновато выйти мне теперь.

Тут кое – что мешает мне немного:

Волшебный знак у вашего порога. Ф а у с т

Так пентаграмма этому виной?

Но как же бес пробрался ты за мной?

Каким путём впросак попался?

М е ф и с т о ф е л ь

Изволили её вы плохо начертить.

И промежуток в уголку остался,

Там, у дверей, - и я свободно мог вскочит

Картину раз высматривал сапожник

И в обуви ошибку указал;

Взяв тотчас кисть, исправился художник

Вот, подбочась, сапожник продолжал:

«Мне кажется лицо немного криво…

А эта грудь, не слишком ли нага…»?

Тут Апеллес прервал нетерпеливо:

«Суди дружок не выше сапога!»

Есть у меня приятель на примете:

Не ведаю, в каком бы он предмете

Был знатоком, хоть строг он на словах,

Но черт его несет судить о свете:

Попробуй он судить о сапогах!

Андрей Чернов, исследуя памятник древнерусской культуры Х II века «Слово о полку Игореве», пришёл к выводу , что структура произведения подчиняется математическому закону .

Что же касается поэтов, то здесь в первую очередь следует назвать гениального грузинского поэта Шота Руставели. Как показали новейшие исследования академика Г. В.Церетели, в основе строения поэмы Ш.Руставели«Витязь в тигровой шкуре» положены симметрия и золотое сечение. В частности, из 1587 строф поэмы больше половины 863-построены по пропорции золотого сечения.

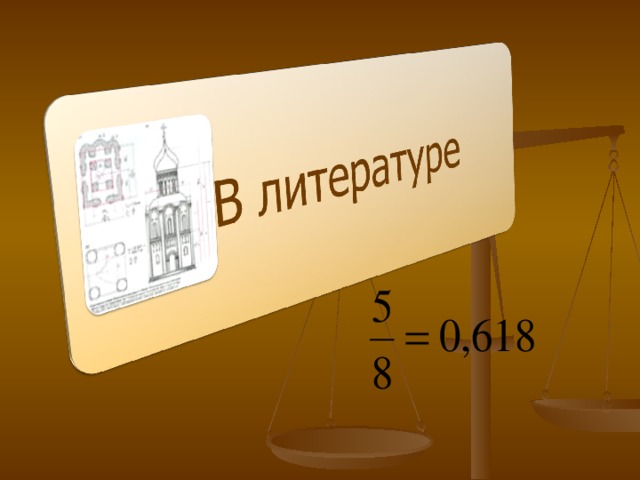
В искусстве

Если золотой прямоугольник использовался художниками для создания у зрителя ощущения покоя, уравновешенности, то золотая спираль, напротив, применялась для выражения тревоги, бурных событий.

Избиение младенцев»

Рафаэль, 1509 г.

В живописи

Мотивы золотого сечения просматриваются в картинах Рафаэля:

Афинская школа Бракосочетание

Выводы

Мир живой природы предстает перед нами совсем иным - подвижным, изменчивым и удивительно разнообразным. Жизнь демонстрирует нам фантастический карнавал разнообразия и неповторимости творческих комбинаций! Мир неживой природы - это прежде всего мир симметрии, придающий его творениям устойчивость и красоту. Мир природы - это прежде всего мир гармонии, в которой действует "закон золотого сечения".

Таким образом всё в нашем мире без исключения подчиняется закону золотого сечения и это всегда было есть и будет.

Золотое сечение часто называют божественной мерой красоты, сутью гармонии и равновесия в мире.

Ссылки

http://www.trinitas.ru/
Геометрия: красота и гармония. Простейшие задачи аналитической геометрии на плоскости. Золотая пропорция. Симметрия вокруг нас. 8-9 классы: элективные курсы/авт.-сост. Л.С. Сагателова, В.Н. Студенецкая. – Волгоград: Учитель, 2007. – 158с.
Математика: наглядная геометрия: учеб. Для учащихся 6 кл.общеобразова. учреждений/ Т.Г. Ходот ,А.Ю.Ходот. – М.: Просвещение, 2007. – 143с.
http://gs.edunet.uz/viskust.htm
http:// goldsech.narod.ru/
http:// http://www.abc-people.com/idea/zolotsech/
http://infoglaz.ru/wp-content/uploads/6d335b4c.jpg
http://www.davidicke.com/wordpress/wp-content/uploads/legacy_images/stories/9388goldenratio.jpg
http://img0.liveinternet.ru/images/attach/c/6/93/366/93366046_large_3726295_20121101_183155.jpg