Муниципальное казенное общеобразовательное учреждение
«Богучарская средняя общеобразовательная школа № 1»
Научно-исследовательская работа
по теме: «Треугольник Паскаля»
Автор: Карпенко Софья Владимировна 8 «А» класс
Руководитель: Алабина Галина Юрьевна
Богучар 2015
Оглавление
Введение
Основная часть
Теоретическая часть работы
а) Блез Паскаль – французский математик
б) треугольник Паскаля как разновидность треугольника
в) свойства треугольника Паскаля и их применение в решении
задач
Практическая часть работы
а) составление последовательности тренировочных задач
по теме «Треугольник Паскаля»
б) создание презентации «Треугольники вокруг нас»
Заключение
Актуальность проекта
Данный проект предназначен для выявления того, насколько широко треугольники используются в практической жизни.
Новизна проекта
Новизна моего исследования состоит в том, что я попыталась показать связь треугольников с жизнью.
Практическая значимость проекта
Данный проект может быть использован как дополнительный материал к урокам геометрии, для внеклассной работы по математике.
Цель проекта
- ознакомиться с треугольником Паскаля как разновидностью треугольников;
- рассмотреть применение треугольника Паскаля в различных сферах;
Гипотеза
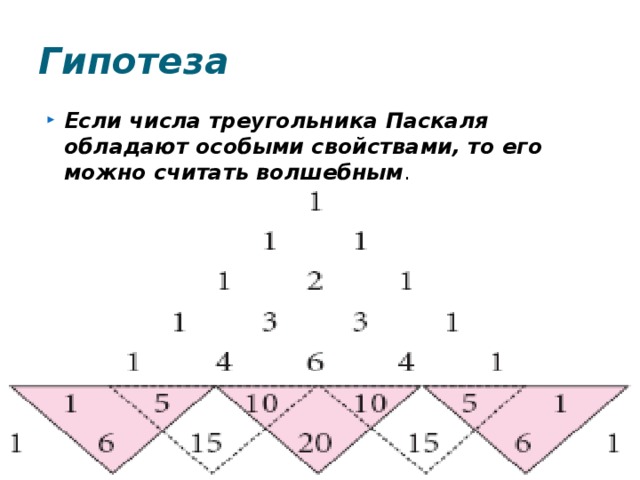
Если числа треугольника Паскаля обладают особыми свойствами, то его можно считать волшебным.
Задачи
- изучить литературу по теме «Треугольник Паскаля»;
- выявить свойства чисел, входящих в состав треугольника Паскаля;
- определить применение свойств чисел треугольника Паскаля;
- сформулировать вывод и итоги исследования;
Объект исследования: треугольник как геометрическая фигура
Предмет исследования: свойства треугольника Паскаля
Методы исследования:
- аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
- поиск информации в интернет - ресурсах.
Направления работы:
- выбор проблемы, источников литературы, составление плана;
- работа с литературой и другими источниками;
- обработка полученных данных;
- анализ результатов, формулирование вывода;
Основные этапы проекта: подготовительный; деятельностный;
ход исследования; рефлексивный; аналитический; презентационный.
Введение
В прошлом учебном году мы начали изучать новый предмет «геометрия».Одна из глав курса геометрии называется «Треугольники». Меня очень заинтересовала данная тема. Я всегда хотела узнать много нового о треугольниках. Ведь мир треугольников очень загадочен и интересен. Я хочу узнать как можно больше о происхождении треугольников, об их значении в нашей жизни.
Треугольник - первая геометрическая фигура, встречающаяся в древних орнаментах. Изучая литературу, я узнала, что в Египте он символизировал триаду духовной воли, любви, интуиции и высшего разума человека, то есть его личность или душу.
Существует множество видов треугольников, но больше всего меня заинтересовал треугольник Паскаля.
Теоретическая часть работы
Б лез Паскаль – французский математик
лез Паскаль – французский математик
Блез Паскаль (19 июня 1623, Клермон-Ферран, — 19 августа 1662, Париж) — французский математик, физик, литератор и философ.
Паскаль был первоклассным математиком. Он помог создать два крупных новых направления математических исследований. В возрасте шестнадцати лет написал замечательный трактат о предмете проективной геометрии и в 1654 году переписывался с Пьером де Ферма по теории вероятностей, что впоследствии оказало принципиальное влияние на развитие современной экономики.
Треугольник Паскаля как разновидность треугольника
Изучая разновидности треугольников, я выяснила, чтотреугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.В действительности, треугольник Паскаля был известен задолго до 1653 года - даты выхода "Трактата об арифметическом треугольнике". Так, этот треугольник воспроизведен на титульном листе учебника арифметики, написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников.
Ещё я узнала из книги "Математические новеллы" (М., Мир, 1974) Мартина Гарднера, что "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике".
Изучая специальную литературу, я узнала, что еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес. Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Треугольник Паскаля имеет применение в теории вероятностей и обладает замечательными свойствами.
Свойства треугольника Паскаля и их применение в решении задач
Изучая свойства треугольника Паскаля, я рассмотрела одно из свойств биномиальных коэффициентов:
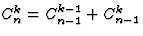
Данное равенство показывает, что биномиальные коэффициенты можно последовательно выписывать в виде треугольной таблицы, которая называется треугольником Паскаля. В n-ой строке треугольника Паскаля стоят коэффициенты разложения 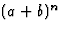 , причем каждый коэффициент, кроме крайних двух, которые равны 1, равен сумме соответствующих коэффициентов из предыдущей строки.
, причем каждый коэффициент, кроме крайних двух, которые равны 1, равен сумме соответствующих коэффициентов из предыдущей строки.
Я узнала, что треугольник Паскаля - это бесконечная числовая таблица "треугольной формы", в которой по боковым сторонам стоят единицы и всякое число, кроме этих боковых единиц, получается как сумма двух предшествующих чисел. В такой форме треугольник Паскаля появился в сочинении Паскаля "Трактат об арифметическом треугольнике", изданном в 1665 г. уже после смерти автора.

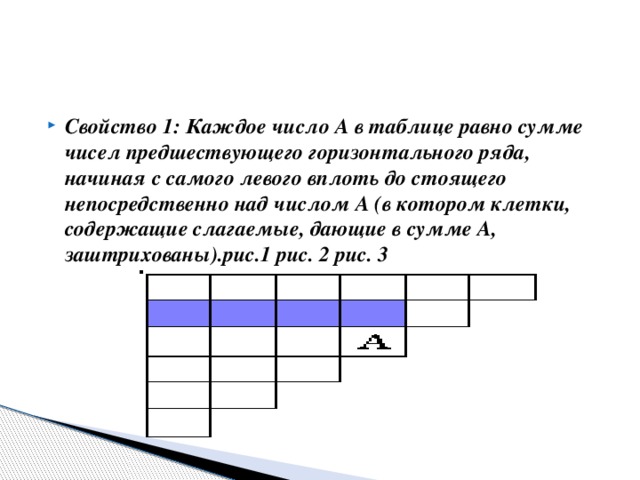
Паскаль подробно исследовал свойства и применения своего "треугольника". Приведу для примера лишь 3 свойства "треугольника", найденные самим Паскалем; при этом буду исходить из того расположения "треугольника" на плоскости, какое было указанно Паскалем, и говорить о горизонтальных и вертикальных рядах. Свойство 1: Каждое число А в таблице равно сумме чисел предшествующего горизонтального ряда, начиная с самого левого вплоть до стоящего непосредственно над числом А (в котором клетки, содержащие 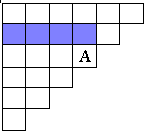 слагаемые, дающие в сумме А, заштрихованы).
слагаемые, дающие в сумме А, заштрихованы).
рис.1 рис. 2 рис. 3
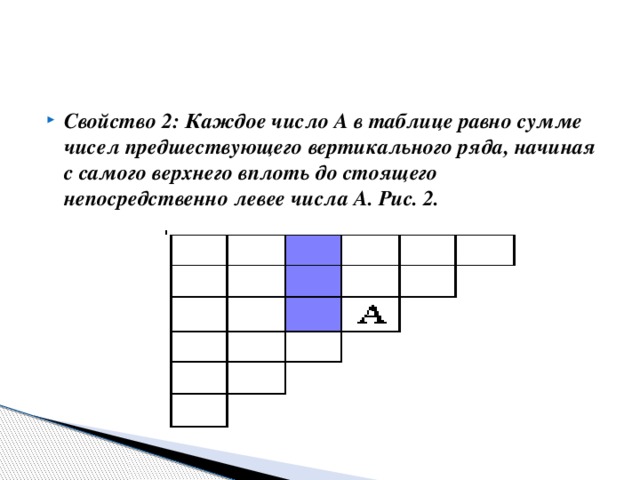
Свойство 2: Каждое число А в таблице равно сумме чисел предшествующего вертикального ряда, начиная с самого верхнего вплоть до стоящего непосредственно левее числа А. 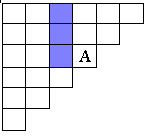 Рис. 2. Свойство 3: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются).
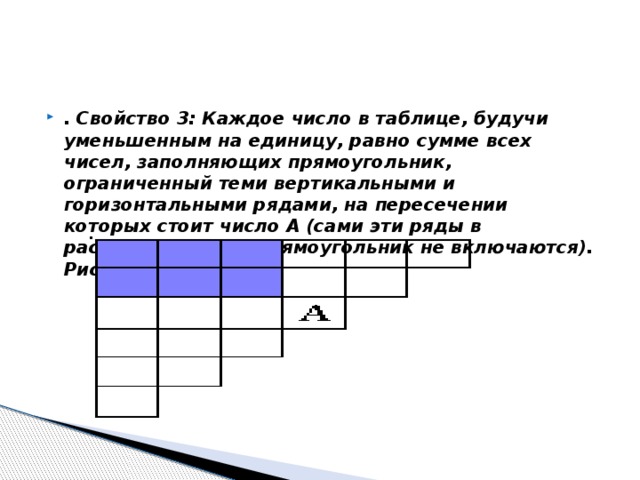
Рис. 2. Свойство 3: Каждое число в таблице, будучи уменьшенным на единицу, равно сумме всех чисел, заполняющих прямоугольник, ограниченный теми вертикальными и горизонтальными рядами, на пересечении которых стоит число А (сами эти ряды в рассматриваемый прямоугольник не включаются). Рис. 3.
Рис. 3.
Я пришла к выводу, что рассмотренные свойства треугольника Паскаля подтверждают слова Мартина Гарднера о том, что треугольник Паскаля одна из наиболее изящных схем во всей математике.
Актуальность исследования обусловлена ежегодным усложнением заданий ГИА и ЕГЭ, что требует углубленных знаний не только в алгебре, но и в геометрии.
Практическая часть работы
Я рассмотрела схему построения треугольника, предложенную Гуго Штейнгаузом в его классическом «Математическом калейдоскопе»: предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно - розовыми. Это один из вариантов построения треугольника.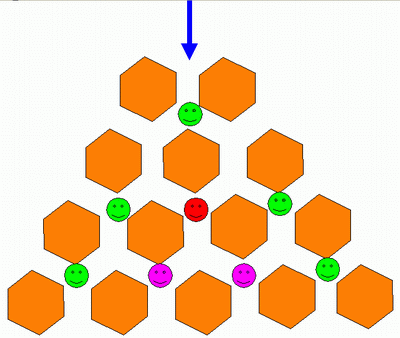
Задача 1.В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбрать из них 3 набора?
Р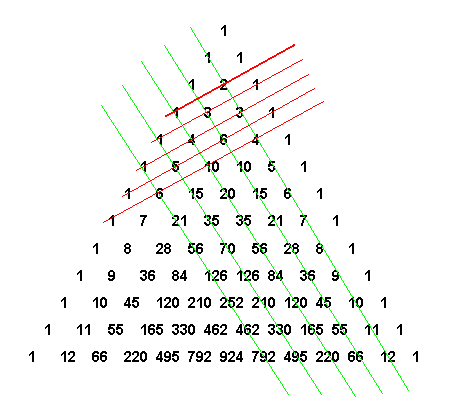 ешение:
ешение:

В
 треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
треугольнике Паскаля число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-ой диагонали и n-ой строки.
Найду диагональ восьмую сверху и отсчитываю три числа по горизонтали. Получу число 56.
Задача 2.Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
Р ешение:
ешение:
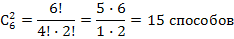


Найду диагональ шестую сверху и отсчитываю два числа по горизонтали. Получу число 15.
Задача3. В пачке находятся одинаковые по размеру 7 тетрадей в линейку и 5 в клетку. Из пачки наугад берут 3 тетради. Какова вероятность того, что все три тетради окажутся в клетку?
Р
 ешение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
ешение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей 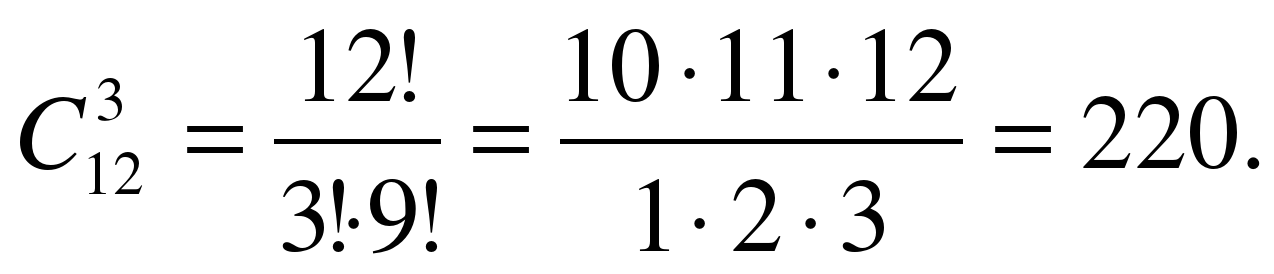
А сколькими способами мы можем выбрать 3 тетради в клетку из имеющихся 5 тетрадей?

Вероятностью Р наступления случайного события А называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов: Р(А)= m/n.
По формуле нахождения вероятности получим
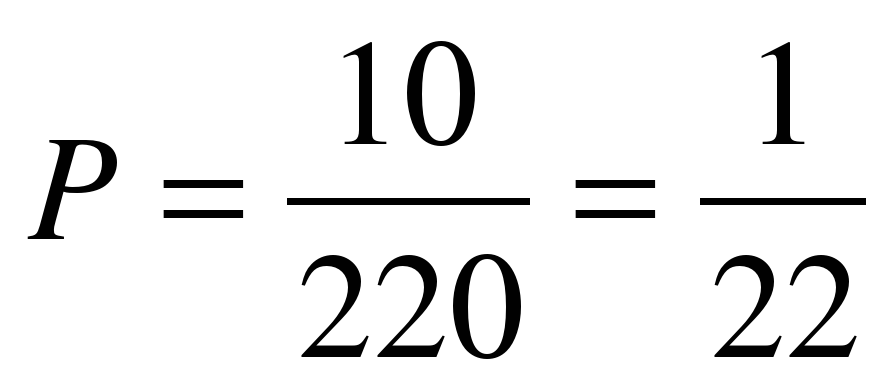
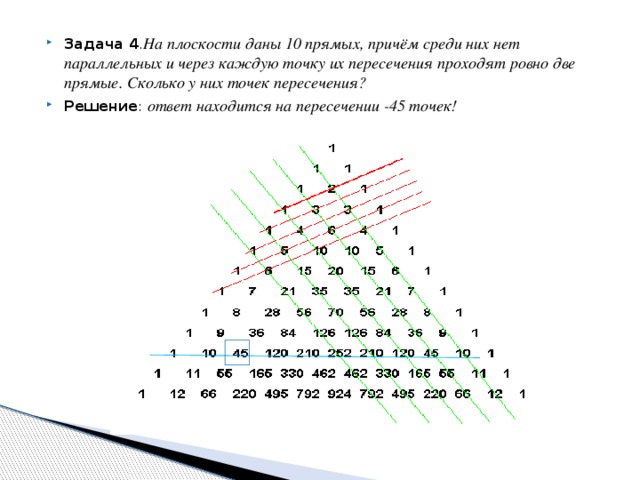
Задача4.На плоскости даны 10 прямых, причём среди них нет параллельных и через каждую точку их пересечения проходят ровно две прямые. Сколько у них точек пересечения?
Р ешение: ответ находится на пересечении -45 точек!
ешение: ответ находится на пересечении -45 точек!

Задача 5.
В сумке 10 мячей, пронумерованных от 1 до 10. Наугад вынимают 2 мяча. Какова вероятность того, что это будут мячи с номерами 7 и 3?
Вынуть 2 мяча из 10 имеющихся можно 45 способами. Вероятность нашего события 2 из 45.
Заключение
Работа по выбранной теме осуществлялась в полном соответствии с планом исследования, а именно: объект и предмет исследования, поставлены цели и задачи, а также определены ожидаемые результаты. Были указаны используемые методы исследования, определена проблема.
В данной работе была дана общая характеристика треугольника как геометрической фигуры, был детально рассмотрен треугольник Паскаля, его свойства.
Я пришла к выводу, что одной из наиболее известных и изящных численных схем во всей математике является треугольник Паскаля. Треугольник Паскаля - понятие значительно шире, чем мне представлялось. Он обладает не только удивительными свойствами, но и применялся в архитектуре средних веков для построения схем пропорциональности и для построения прямых углов землемерами и архитекторами. Используя треугольник Паскаля, можно решить задачи из теории вероятности.
Практическая значимость данной работы заключается в следующем:
я, изучив много литературы по данному вопросу, получила дополнительные знания в области математики, укрепила свой интерес к этой науке. Работа по данной теме оказалась интересной и полезной.
Список использованных источников и литературы
1. Абачиев С. К. Радужная фрактальность треугольника Паскаля
2. Мартин Гарднер. Глава 17. Неисчерпаемое очарование треугольника Паскаля // Математические новеллы. — М.: Мир, 1974. — 456 с. 3. Треугольник Паскаля. В. А. Успенский. - 2 - е изд. – М.: Наука, 1979. – 48с.
4. Удивительный треугольник великого француза // Hard'n'Soft № 10 2003
5. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17-25.
6. Энциклопедия для детей. Т 11. Математика / Глав. ред. М. Аксенова; метод. и отв. ред. В. Володин. – М.: Аванта+,2004. – 688с.
7. http://ru.wikipedia.org/wiki/
8. Weisstein, Eric W. Pascal's Triangle (англ.) насайте Wolfram MathWorld.
 лез Паскаль – французский математик
лез Паскаль – французский математик




 ешение:
ешение:
 треугольнике Паскаля
треугольнике Паскаля ешение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей
ешение. Сначала найдём общее число возможных исходов, т.е. сколькими способами мы можем выбрать 3 тетради из 12 тетрадей