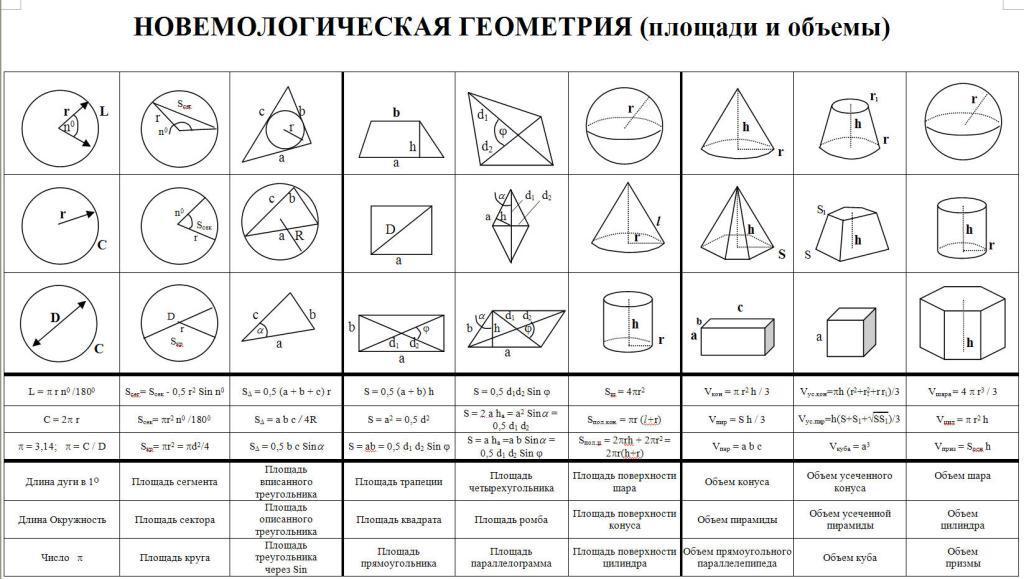
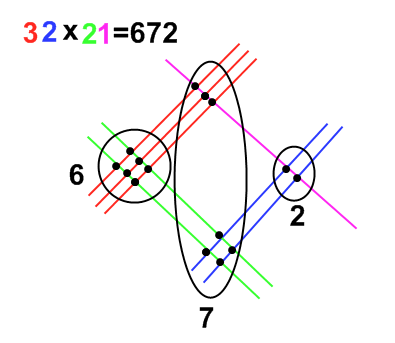
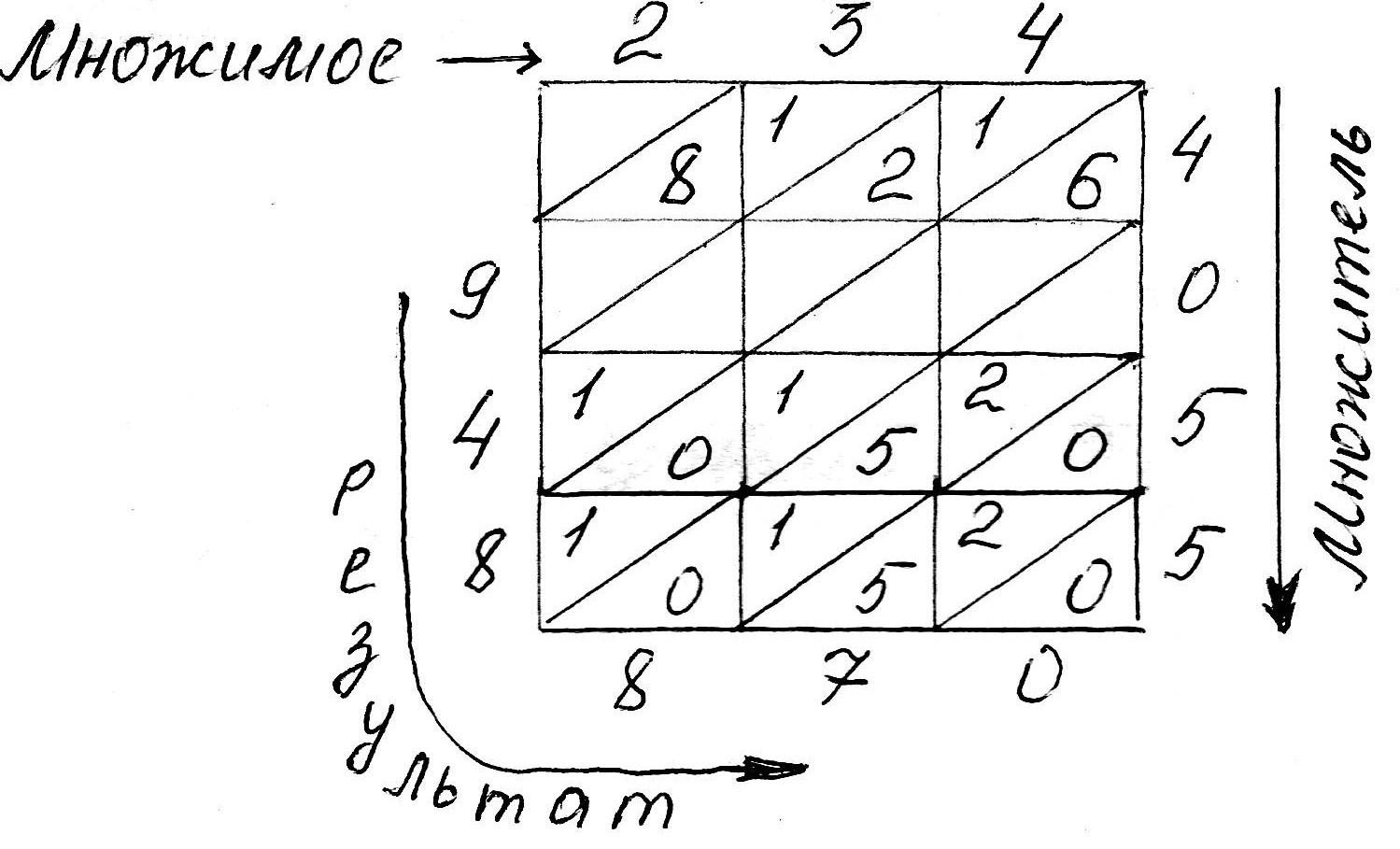
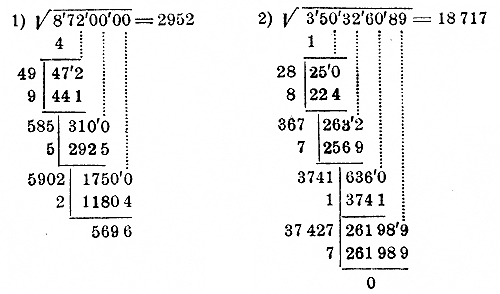
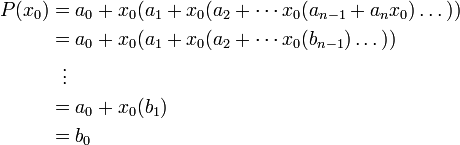Мастер-класс по математике "Красота привлекает, исследование увлекает." Удивляться - значит жить! А чем можно удивить учащихся на уроках математики? Только тем, что для тебя самого по - настоящему интересно, а для них - необычно. Вот и мы постарались показать обычное.умножение многозначных чисел не совсем обычными способами; обычное.извлечение квадратного корня.без использования технических средств обучения.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Мастер - класс "Красота привлекает, исследование увлекает..."
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Мастер - класс "Красота привлекает, исследование увлекает..." »
Автор: Пронина Светлана Михайловна, Тептя Татьяна Петровна
Дата: 03.04.2015
Номер свидетельства: 196740
Полезное для учителя
Распродажа видеоуроков!
1970 руб.
2820 руб.
1790 руб.
2560 руб.
2000 руб.
2860 руб.
2220 руб.
3170 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства