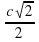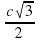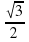КГУ «Общеобразовательная средняя школа №3 им. Ю.А. Гагарина»
отдела образования Шемонаихинского района»
Интеллектуальная игра
«Путешествие
на родину Пифагора»
ВНЕКЛАССНОЕ МЕРОПРИЯТИЕ
ПО МАТЕМАТИКЕ
Подготовила:
учитель математики Миронова С.П.
г. Шемонаиха, 2017 год
Цели:
организация деятельности обучающихся по закреплению теоремы Пифагора и применению полученных знаний;
развитие математических способностей, сообразительности, логического мышления, укрепление памяти учащихся;
привитие интереса к математике;
развитие коммуникативных возможностей учащихся;
Задачи:
Образовательные: обеспечить закрепление и применение темы теорема Пифагора при решении задач, формировать умение самостоятельно решать задачи, используя теорему Пифагора.
Развивающие: содействовать развитию логического мышления, развивать умения сравнивать, анализировать, делать выводы, вырабатывать умение систематизировать и обобщать, развивать познавательный интерес и расширять кругозор.
Воспитательные: воспитывать чувства ответственности, дисциплинированности, аккуратности, умения сочетать индивидуальную работу с коллективной.
Ожидаемые результаты обучения:
Учащиеся должны знать: понятие «пифагоровы тройки», «египетские треугольники», формулировку и доказательство теоремы Пифагора
Учащиеся должны уметь: формулировать и доказывать теорему Пифагора, применять теорему для нахождения неизвестных сторон прямоугольного треугольника (вычислять гипотенузу и катеты прямоугольного треугольника).
Тип занятия: игра.
Форма: фронтальная; групповая; индивидуальная.
Участники игры: учащиеся 8 класса.
Оборудование и материалы: Учебник, интерактивная доска, проектор, компьютер, презентация, карточки с заданиями, ЦОР «Пифагоровы треугольники».
Ход игры
I. Организационный момент
1. Приветствие.
Эпиграф урока (Слайд 1. Приложение 1. Путешествие на родину Пифагора).
«Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора»
Иоганн Кеплер
(Слайд 2. Приложение 1. Путешествие на родину Пифагора).
Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
На радужной узрел я оболочке
Бегущие квадратики, кружочки,
Вселенной опрокинутый узор,
И вспыхнуло в мелькании сквозь строчки
Пылающее имя-Пифагор!
(Слайд 3. Приложение 1. Путешествие на родину Пифагора).
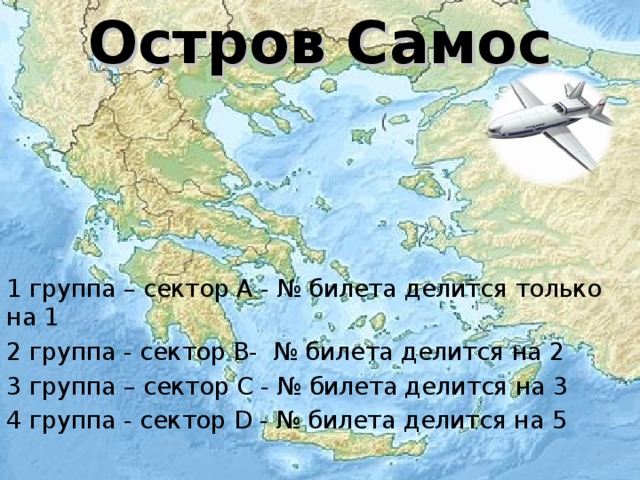
Ребята, сегодня мы совершим путешествие на остров Самос, расположенный в Эгейском море. На этом острове жил величайший древнегреческий математик Пифагор. Мы узнаем, чем он интересен и какие «математические события» там происходили. Путешествовать мы будем на самолете.
2. Деление на группы.
Чтобы отправиться в полёт вам необходимо приобрести билеты и разделиться на группы (Приложение 2. Билеты)
1 группа – сектор А - № билета делится только на 1
2 группа - сектор В- № билета делится на 2
3 группа – сектор С - № билета делится на 3
4 группа - сектор D - № билета делится на 5
Прошу Вас занять свои места в салоне самолёта, согласно купленным билетам. Проверить готовность к полету. Все готово?
II. Проведение игры
1 тур «Разминка» (Слайд 4. Приложение 1. Путешествие на родину Пифагора)
Чтобы пройти таможенный контроль, надо ответить на вопросы (фронтальная беседа, проводится с помощью технологии «Микрофон»)
Чему равен квадрат гипотенузы в прямоугольном треугольнике?
Продолжи запись с2= …
Как найти катет а по т. Пифагора?
Чему равен катет b по т. Пифагора?
Какие треугольники являются египетскими?
Правильные ответы фиксируются в оценочной таблице
2 тур «Реши задачку »(Слайд 5. Приложение 1. Путешествие на родину Пифагора)
За каждый правильный ответ 1 балл.
Учащимся предлагаются задачи, которые необходимо решить задачи (Задание №1 за 5 мин, Задание №2 за 7 мин)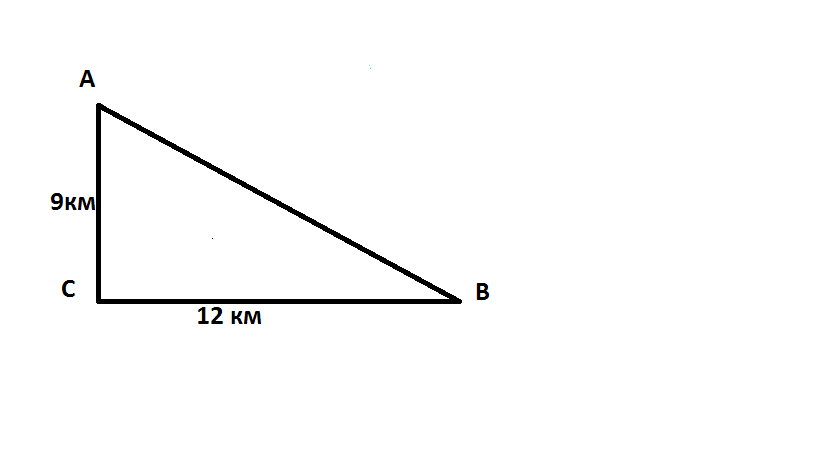
Задание №1. Мы с вами в самолете. Он находится на высоте 9 км. На земле мы преодолели расстояние 12км. Какой путь пролетел самолет в воздухе с момента взлета?
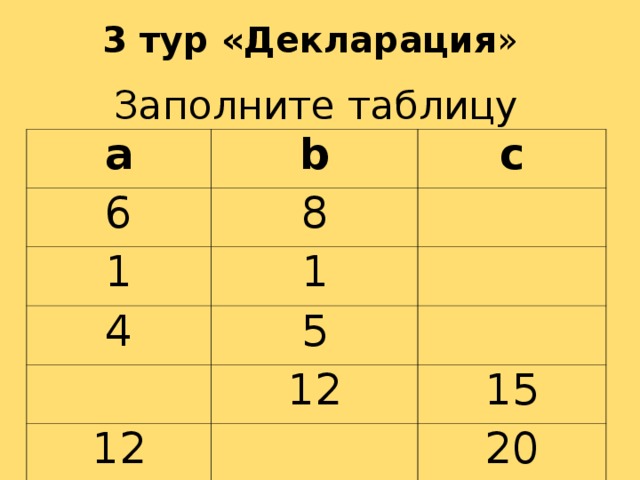
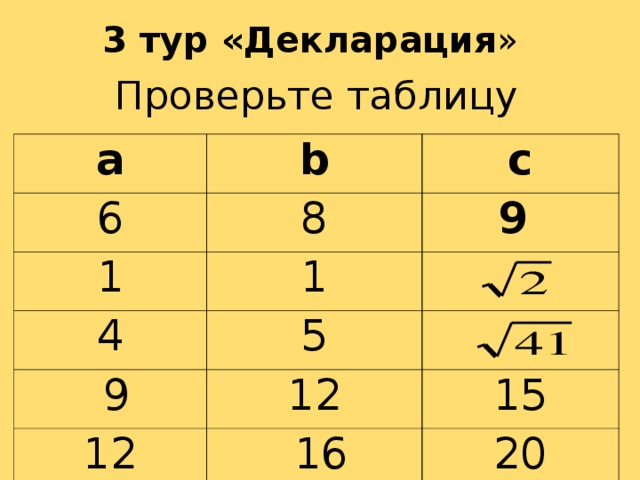
3 тур «Декларация» (Слайд 6,7. Приложение 1. Путешествие на родину Пифагора)
Задание №2. Работа в группах. В самолете путешественники заполняют декларацию. Дана таблица, в которой а и b – катеты, с – гипотенуза.
| а | b | с |
| 6 | 8 |
|
| 1 | 1 |
|
| 4 | 5 |
|
|
| 12 | 15 |
| 12 |
| 20 |
Самопроверка по слайду. Сравниваем полученные ответы. (Слайд 5. Приложение 1. Путешествие на родину Пифагора)
Мы прибыли на остров Самос. После долгого перелёта нам нужно размяться. Физминутка (дети отвечают жестами и движениями)
Историческая справка. (Слайд 8. Приложение 1. Путешествие на родину Пифагора).
Нас встречает экскурсовод …. и рассказывает о Пифагоре. Сообщение о Пифагоре (индивидуальное задание, работа с одаренными детьми)
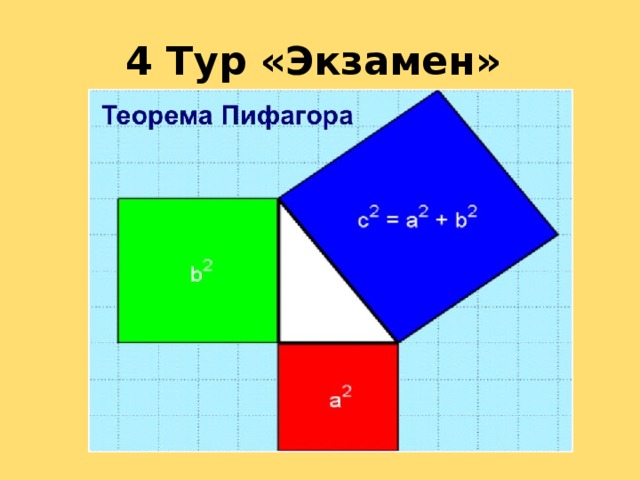
4 Тур «Экзамен» (Слайд 9. Приложение 1. Путешествие на родину Пифагора).
По традиции острова всякий прибывающий на остров сдает экзамен на право быть пифагорейцем. Каждый участник группы рассказывает теорему Пифагора лидеру группы. (Приложение 3.Лист оценивания)
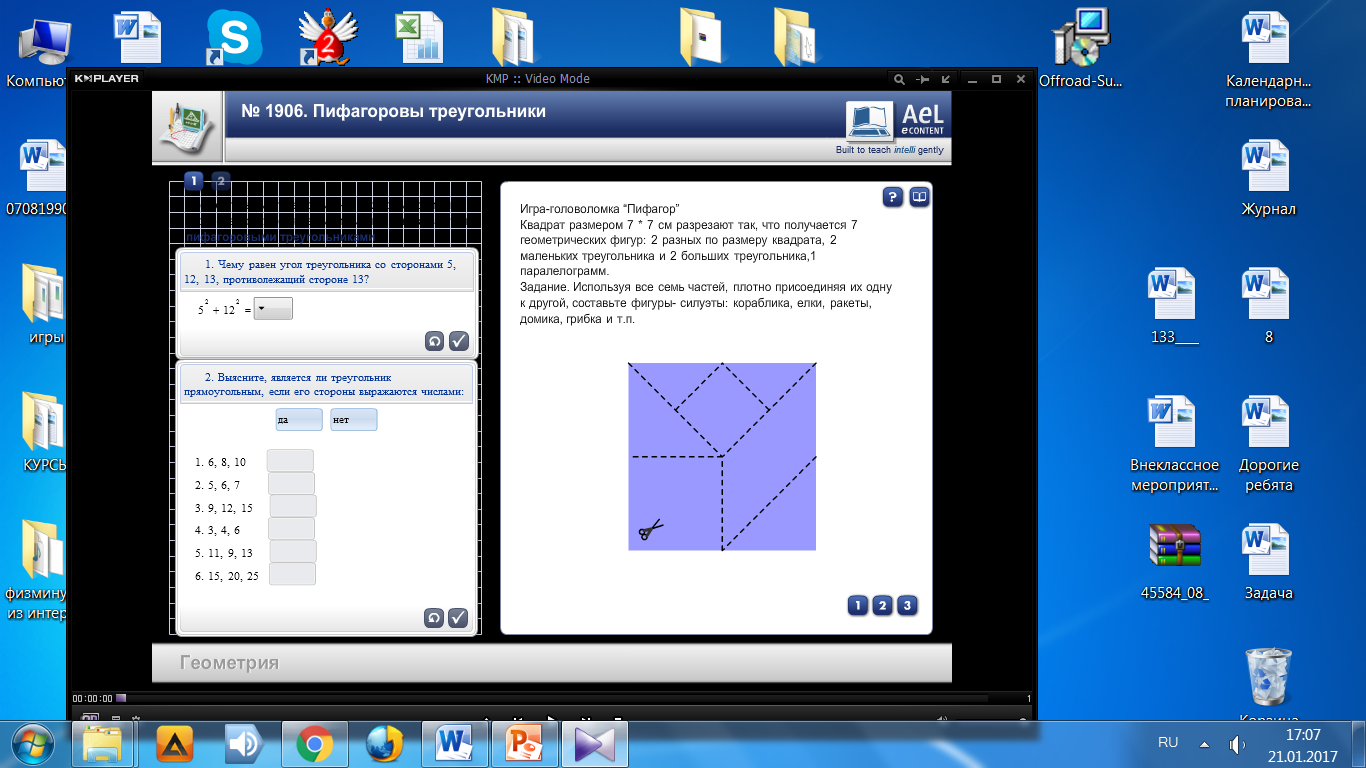
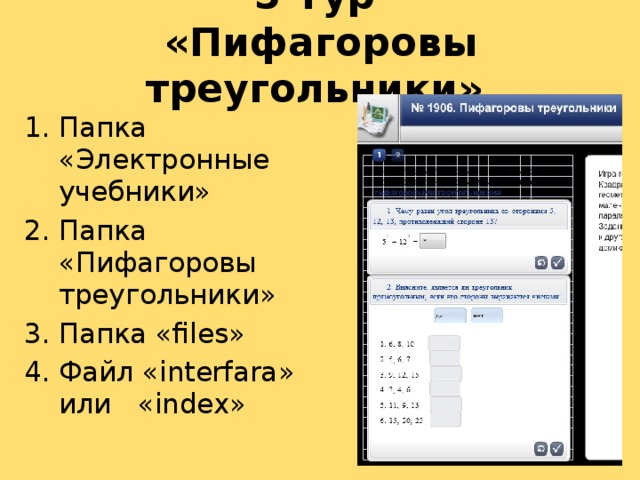
5 Тур «Пифагоровы треугольники»
Пифагор был четыре раза подряд олимпийским чемпионом. Давайте проведем состязание. У каждой группы на столах есть ноутбуки, на них учащиеся выполняют интерактивные задания. (Слайд 10. Приложение 1. Путешествие на родину Пифагора)
Папка «Пифагоровы треугольники» на рабочем столе
Папка «files»
Файл «interfara» или «index»
Задание 2. Выясните, является ли треугольник прямоугольным, если его стороны выражаются числами.
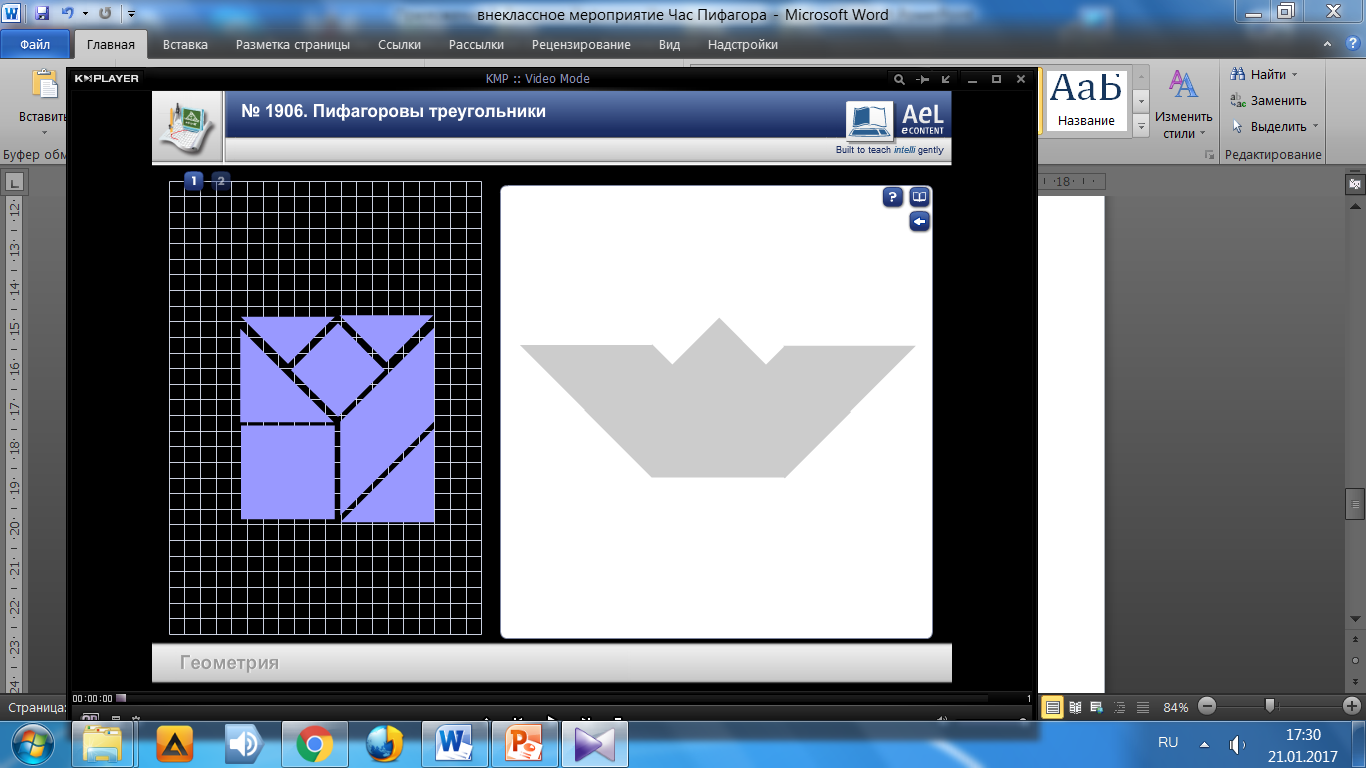
6 Тур «Танграм»
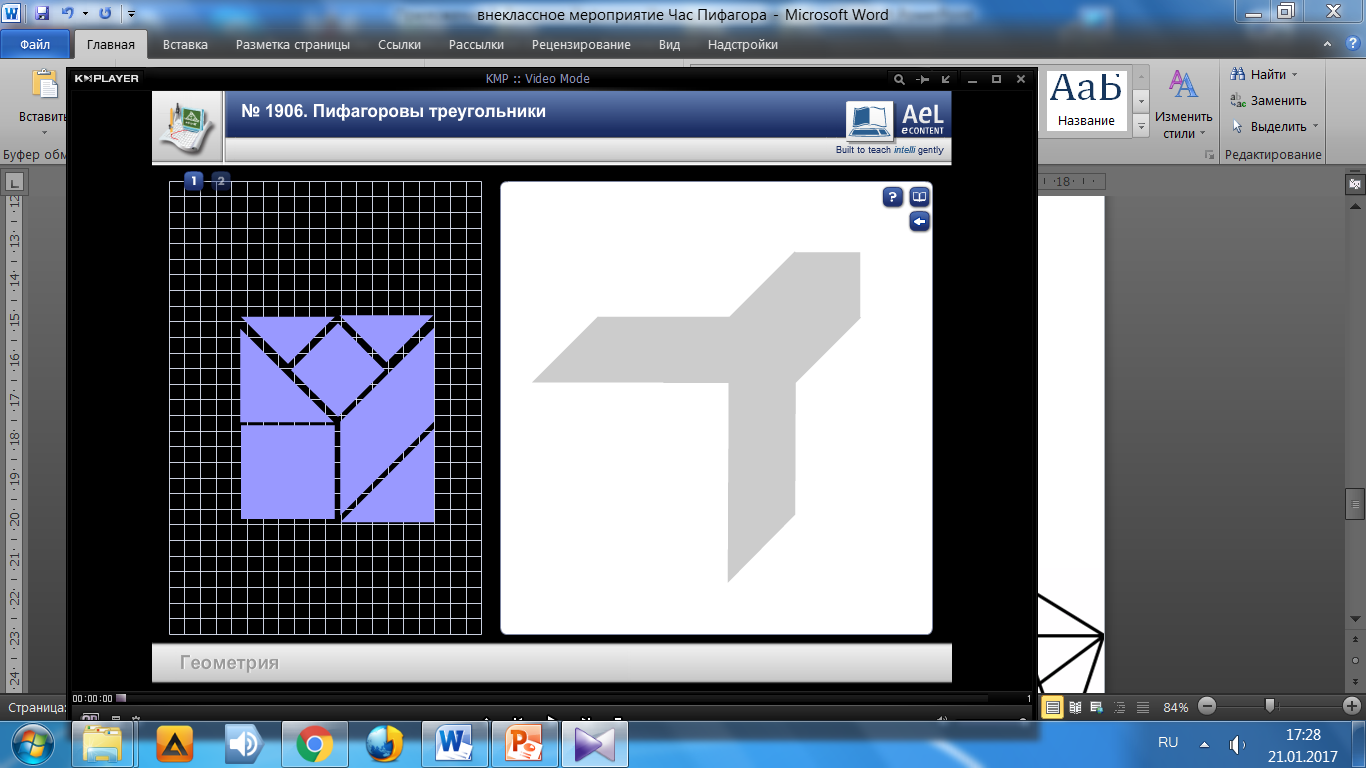
Квадрат, разделенный на семь частей : 2 квадрата, 2 маленьких и 2 больших треугольника и 1 параллелограмм. Задание: используя все семь частей составьте фигуры – силуэты: ёлки, ракеты, кораблика. 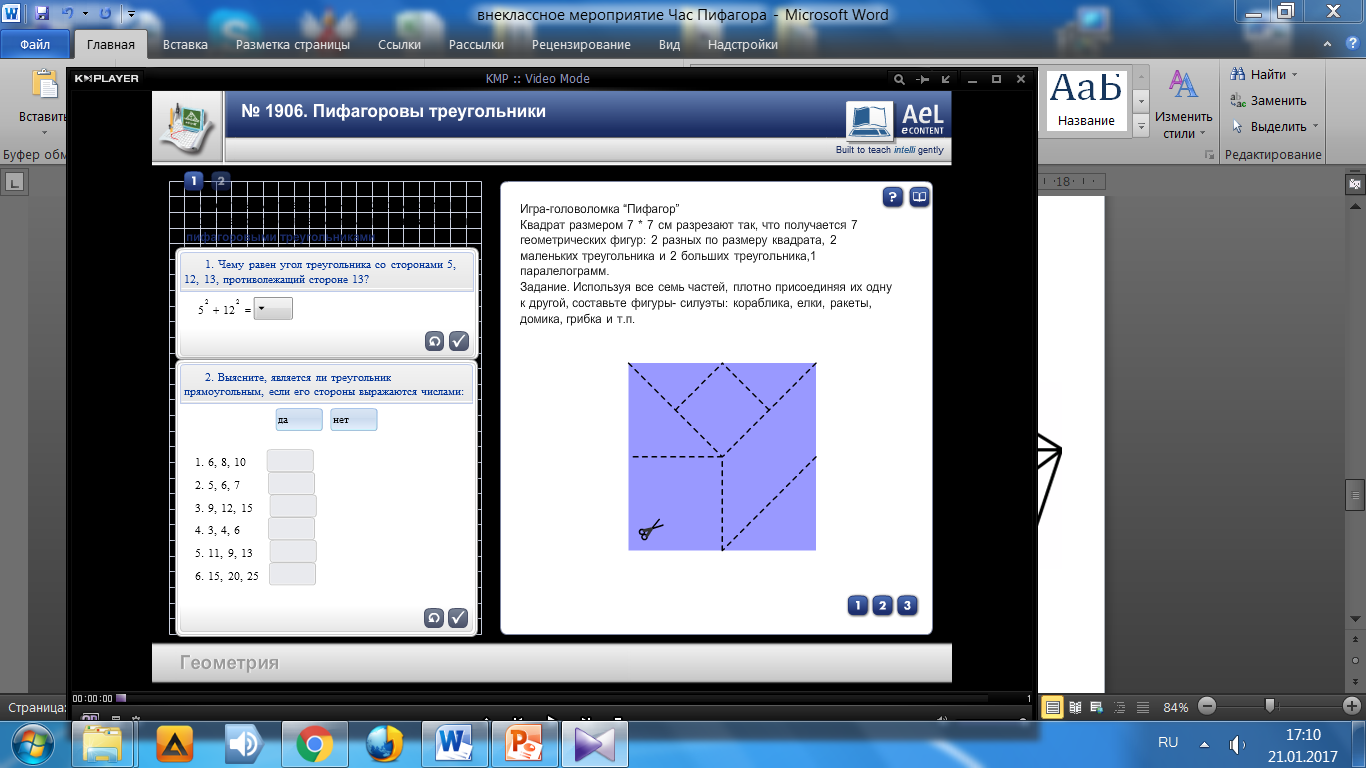
Учащиеся выполняют Интерактивное задание на ноутбуках. Задание 3. Игра - говоломка «Пифагор».
(Слайд 11. Приложение 1. Путешествие на родину Пифагора)
1 группа – №1, 2 группа - №2
3 группа - №3, 4 группа - №1
Задание №1 Задание №2 Задание №3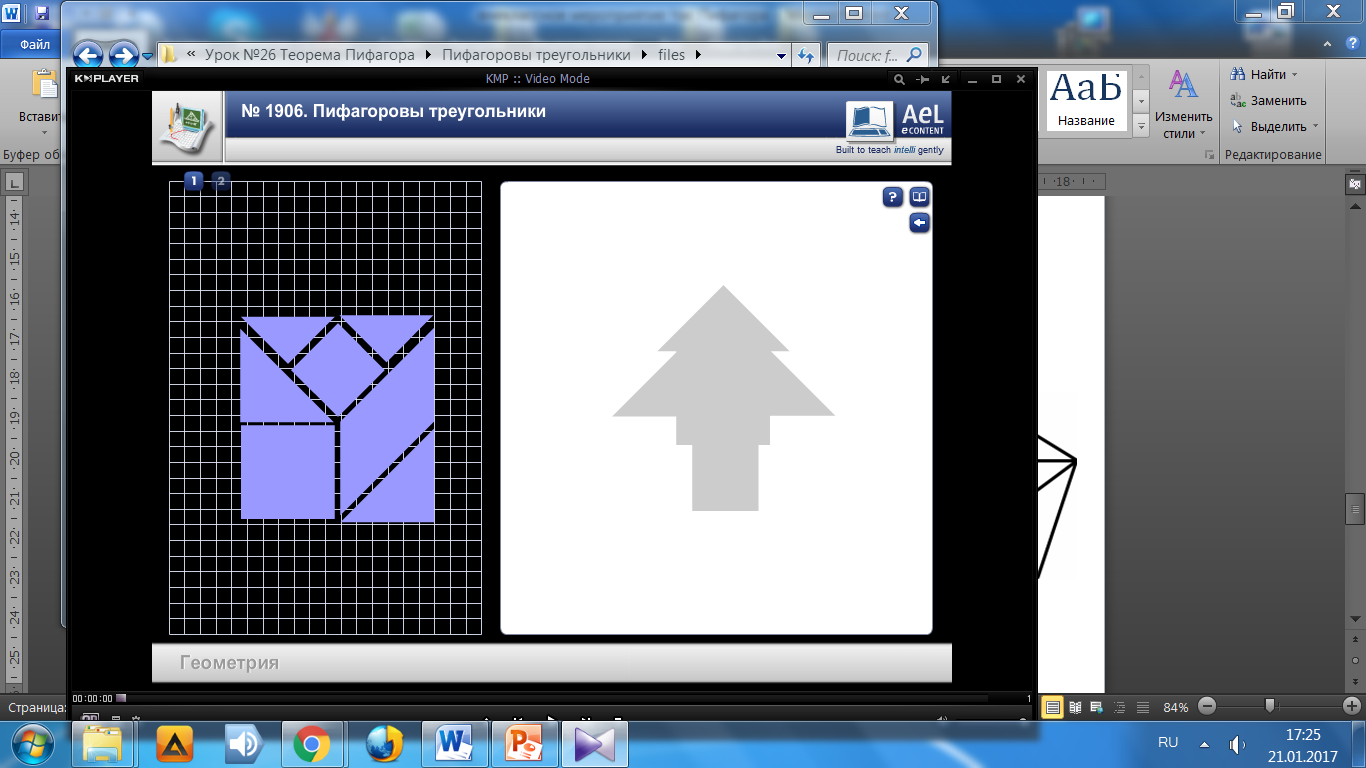
III. Подведение итогов. (Слайд 12. Приложение 1. Путешествие на родину Пифагора)
Мы возвращаемся домой. Подведем итоги нашего путешествия. Учащиеся выставляют оценки в группах. (Приложение 3.Лист оценивания)
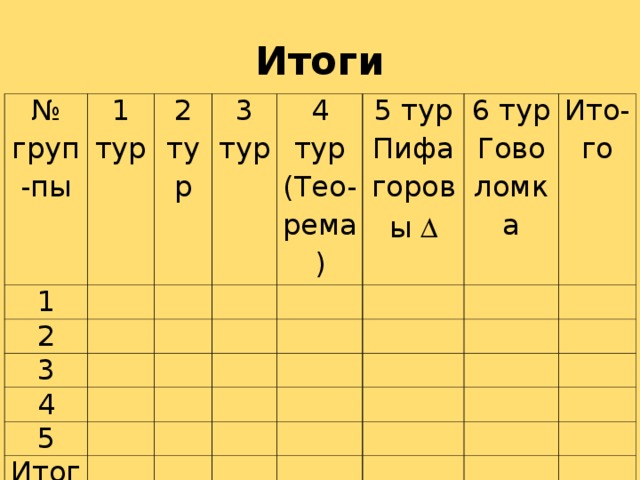
Учитель заполняет на интерактивной доске сводную итоговую таблицу и подводит итоги состязания.
| № группы | 1 тур | 2 тур | 3 тур | 4 тур (Теорема) | 5 тур Пифагоровы треугольники | 6 тур Говоломка | Итого |
| 1 |
|
|
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
| Итого |
|
|
|
|
|
|
|
Награждение победителей. 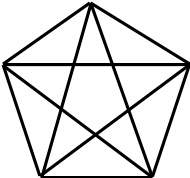
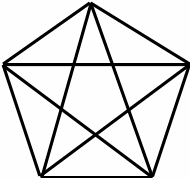
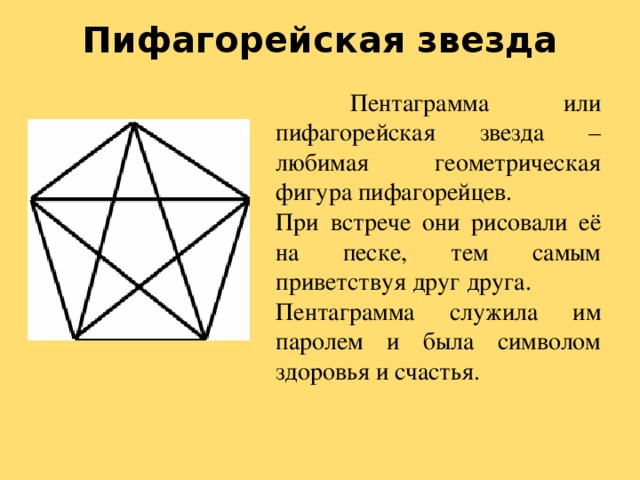
Пентаграмма – это звёздчатый пятиугольник, образованный диагоналями правильного пятиугольника. Пятиконечная звезда считалась в школе Пифагора чем-то вроде талисмана, которым одаривали друзей; тайным знаком, по которому пифагорейцы узнавали друг друга. Пентаграмму никто не изобретал, её только копировали с натуры. Вид пятиконечной звезды имеют цветы, морские звёзды и другие создания природы. Пентаграмма пропорциональна, значит, красива. Не случайно и сегодня она реет на флагах едва ли не половины стран мира. Но первыми, кто обратил пентаграмму в символ, были пифагорейцы.
Пифагорейская звезда была излюбленной геометрической фигурой пифагорейцев, она служила им паролем и была символом здоровья и счастья. Вы становитесь членами нашего ордена. Каждый из вас получает пентаграмму как символ здоровья и счастья. (Всем раздаются пентаграммы). (Слайд 13. Приложение 1. Путешествие на родину Пифагора).
IV. Рефлексия. Теорема Пифагора – одна из главных теорем геометрии. Этой теореме даже посвящены стихи.
О теореме Пифагора
Суть истины вся в том, что нам она – навечно,
Когда хоть раз в прозрении ее увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна.
(Слайд 14. Приложение 1. Теорема Пифагора)
Если вы всё поняли и вам это пригодиться в жизни, то вы выбираете «чемодан».
Если не все понято, надо ещё раз разобрать и кое что доработать, то выбираете «мясорубку».
А если вам полученные знания не нужны, то тогда выбираете «мусорную корзину».
Соотнесите свои знания в соответствии с предложенными.
Напишите ваши рассуждения на стикере и прикрепите к соответствующей картинке.
Список используемой литературы:
Виленкин Н.Я. и др. За страницами учебника математики. М. «Просвещение» АО «Учебная литература» 1996.
Савин А.П. Энциклопедический словарь юного математика. М. «Просвещение» 1995.
Бекбоев И., Абдиев А., Кайдасов Ж., Хабарова Г. Геометрия 8. Алматы: «Мектеп», 2016.
Еленьский Щепан «По следам Пифагора». Москва. Детгиз. 1961 г.
Список использованных Интернет-ресурсов:
http://festival.1september.ru/articles/514101/
http://uchebana5.ru/cont/1671262.html
https://infourok.ru/plan-uroka-po-teme-teorema-pifagora-reshenie-zadach-696849.html
http://e.edu.kz/sui/#/lcms/scorm/530104838
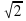
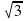
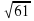
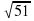
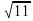
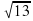
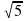 м
м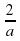
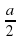
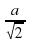 D)
D)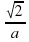
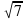
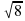
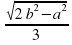
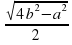
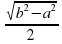 D)
D) 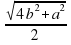
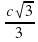 B)
B)