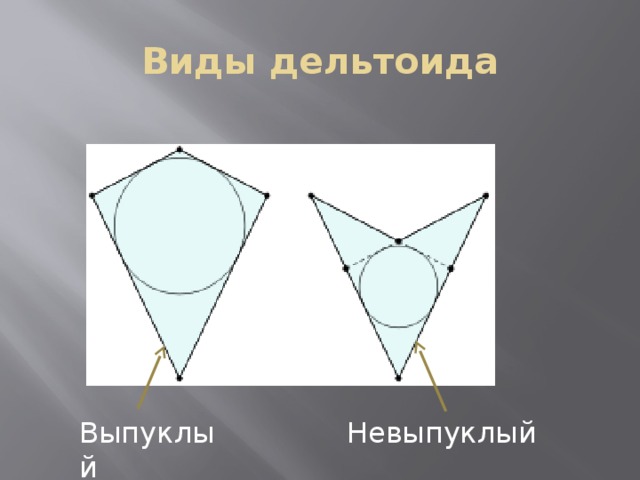
| Фестиваль исследовательских и творческих работ учащихся «Портфолио» Конкурс «Учебный проект» _________________________________________________________________________ |
| Тема: Выпуклый дельтоид на плоскости и в пространстве. |
Автор работы: ученик
СОШ " Средняя общеобразовательная школа № 18"
г. Новокузнецк
Печёнкин А. Е.
Научный руководитель:
преподаватель математики,
Дамм Е.П.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 3
ВЫПУКЛЫЙ ДЕЛЬТОИД 4
Свойства выпуклого дельтоида 4
Признаки выпуклого дельтоида 5
Площади выпуклого дельтоида 7
ВЫПУКЛЫЙ ДЕЛЬТОИДНЫЙ МНОГОГРАННИК 10
Построение дельтоидного многогранника, его виды и свойства 10
Площади боковой и полной поверхности, объем выпуклого дельтоидного многогранника 11
ЗАКЛЮЧЕНИЕ 15
СПИСОК ЛИТЕРАТУРЫ 16
ВВЕДЕНИЕ
Актуальность. В настоящее время в школьном курсе геометрии, изучаются различные геометрические фигуры и тела, такие как круг, треугольник, четырехугольник, многоугольник, тетраэдр, параллелепипед, октаэдр и другие. Большая часть из них исследованы достаточно подробно, но существуют и такие, свойства и признаки которых до конца не изучены наукой – это, в частности, ромбоид, дельтоид, трапецоид, дельтоидный многогранник. В условиях увеличения интенсивности обучения геометрии, усложнения задач в итоговых аттестациях выпускных классов, наличия во второй части ЕГЭ задач, требующих углубленных знаний в области планиметрии и стереометрии, разработка научно обоснованного методического материала по таким фигурам позволит как существенно сократить время решения задач, так и будет способствовать более простым и изящным способам их решения. Кроме того, в прикладном плане научные знания о выпуклом дельтоиде и дельтоидном многограннике могут быть полезны при разработке и конструировании планеров летательных аппаратов, воздушных змеев, плавательных судов, а так же в области архитектуры и дизайна при создании рисунков декоративной мозаики. Поэтому, исследование свойств и признаков этих геометрических фигур на примере выпуклого дельтоида и выпуклого дельтоидного многогранника в настоящее время представляется весьма актуальной задачей.
Объектом исследования является выпуклый четырехугольник дельтоид, а также выпуклый дельтоидный многогранник.
Цель исследования – разработка методических подходов к изучению свойств и признаков выпуклого дельтоида, выпуклого дельтоидного многогранника, вывод формул площадей выпуклого дельтоида, объема, площади боковой и полной поверхности дельтоидного многогранника.
Реализация цели предполагала решение следующих задач:
систематизировать и обобщить понятия четырехугольников и дельтоида;
дать определение выпуклого дельтоида;
дать определение дельтоидного многогранника;
определить виды дельтоидных многогранников;
вывести и доказать новые свойства выпуклого дельтоида, дельтоидного мноогранника;
определить и обосновать признаки выпуклого дельтоида;
вывести формулы площади выпуклого дельтоида;
вывести формулы объема дельтоидного многогранника;
вывести площади боковой и полной поверхности дельтоидного многогранника.
Изучение выпуклого дельтоида, дельтоидного многогранника, их свойств и признаков ранее не было предметом самостоятельного научного анализа. Обоснование новых свойств, признаков выпуклого дельтоида и дельтоидного многогранника, а также вывод формул опирается на использование известных и доказанных теорем, используемых в геометрии, а также свойствами и признаками других геометрических фигур.
Наиболее существенные научные результаты, полученные лично автором, состоят в следующем:
Проведено специальное исследование и обобщение понятий четырехугольника, многоугольника и дельтоида.
Выведены и доказаны четыре новых свойства выпуклого дельтоида, определены и обоснованы его признаки, выведены и доказаны четыре новых формулы нахождения площади выпуклого дельтоида.
Определены виды выпуклого дельтоидного многогранника и дано определение каждому из видов.
ВЫПУКЛЫЙ ДЕЛЬТОИД
Дельтоид – четырёхугольник, обладающий двумя парами сторон одинаковой длины. Равными являются две пары смежных сторон.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Таким образом, выпуклый дельтоид – это четырёхугольник, у которого две пары смежных сторон равны и который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
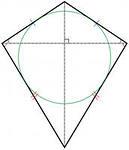
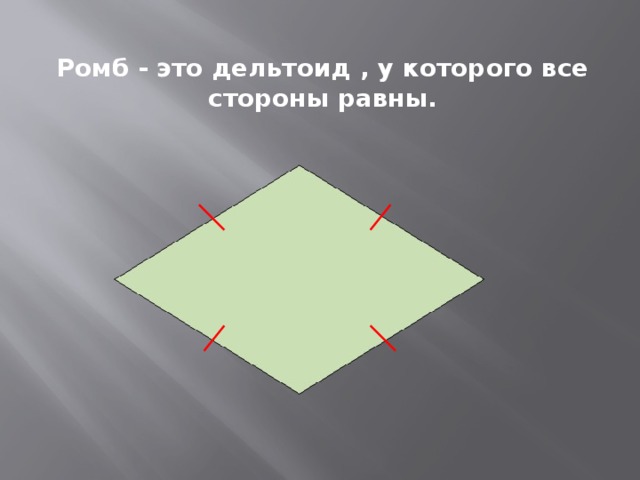
Из определения дельтоида следует, что и ромб, и квадрат также являются дельтоидами. Ромб – это параллелограмм, у которого все стороны равны
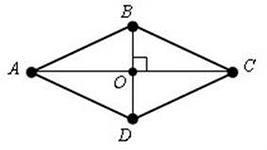
Квадрат – это ромб с прямыми углами. Значит, ромб и квадрат имеют две пары равных смежных сторон.
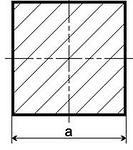
Свойства выпуклого дельтоида.
Выясним, какими свойствами обладает выпуклый дельтоид  , у которого
, у которого 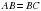 ,
, 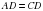 .
.

1) Проведём диагональ  и рассмотрим треугольники
и рассмотрим треугольники 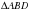 и
и 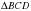 .
.
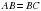 – по условию;
– по условию;
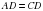 – по условию;
– по условию;
 – общая сторона.
– общая сторона.
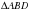 =
=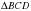 по трём сторонам.
по трём сторонам.
Из равенства треугольников следует, что 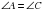 ,
, 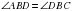 ,
, 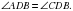 То есть в выпуклом дельтоиде углы между сторонами неравной длины равны и диагональ, соединяющая вершины неравных углов является биссектрисой (
То есть в выпуклом дельтоиде углы между сторонами неравной длины равны и диагональ, соединяющая вершины неравных углов является биссектрисой (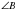 и
и 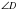 не могут быть равными, так как
не могут быть равными, так как 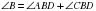 ,
,  , а
, а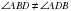 , так как это не углы при основании равнобедренного треугольника, аналогично
, так как это не углы при основании равнобедренного треугольника, аналогично 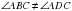 ).
).
2) Проведём диагональ 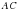 . Рассмотрим треугольники
. Рассмотрим треугольники 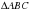 и
и 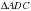 . Они равнобедренные по определению (треугольник называется равнобедренным, если у него две стороны равны0).
. Они равнобедренные по определению (треугольник называется равнобедренным, если у него две стороны равны0).
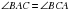 – так как это углы при основании равнобедренного треугольника.
– так как это углы при основании равнобедренного треугольника.
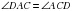 – так как это углы при основании равнобедренного треугольника.
– так как это углы при основании равнобедренного треугольника.
Так как 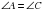 (ранее доказанное, смотрите п.1),
(ранее доказанное, смотрите п.1), 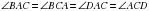 , следовательно
, следовательно 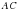 – биссектриса (по определению). Точка
– биссектриса (по определению). Точка 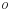 – точка пересечения диагоналей.
– точка пересечения диагоналей. 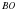 – отрезок биссектрисы
– отрезок биссектрисы 
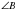 (смотрите выше), проведённый к основанию равнобедренного треугольника
(смотрите выше), проведённый к основанию равнобедренного треугольника 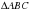 , следовательно,
, следовательно, 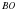 – высота и медиана этого треугольника (значит,
– высота и медиана этого треугольника (значит,  ).
). 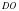 – отрезок биссектрисы
– отрезок биссектрисы 
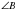 (смотрите выше), проведённый к основанию равнобедренного треугольника
(смотрите выше), проведённый к основанию равнобедренного треугольника 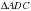 , следовательно,
, следовательно, 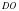 – высота и медиана этого треугольника (значит,
– высота и медиана этого треугольника (значит,  ). Таким образом, диагонали выпуклого дельтоида взаимно перпендикулярны и при пересечении диагоналей, диагональ, соединяющая вершины равных углов, делится пополам.
). Таким образом, диагонали выпуклого дельтоида взаимно перпендикулярны и при пересечении диагоналей, диагональ, соединяющая вершины равных углов, делится пополам.
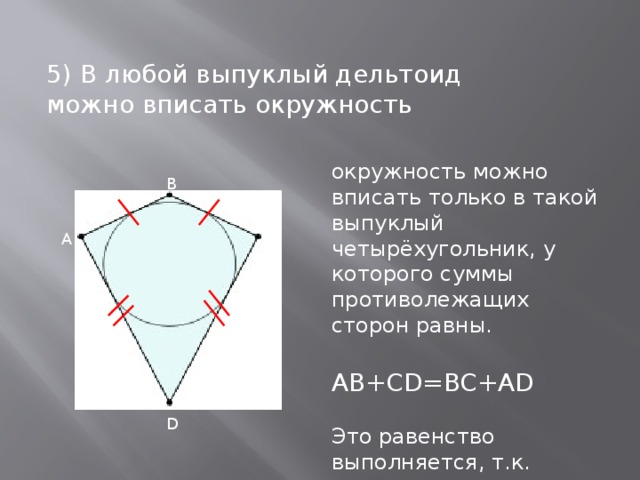
3) Выясним, можно ли вписать в любой выпуклый дельтоид окружность. Известно, что окружность можно вписать только в такой выпуклый четырёхугольник, у которого суммы противолежащих сторон равны. В выпуклом четырёхугольнике  , в котором
, в котором 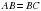 ,
, 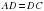 ,
, 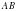 и
и  – противолежащие стороны,
– противолежащие стороны,  и
и  – противолежащие стороны.
– противолежащие стороны.
Вывод:  Следовательно, в любой выпуклый дельтоид можно вписать окружность.
Следовательно, в любой выпуклый дельтоид можно вписать окружность.
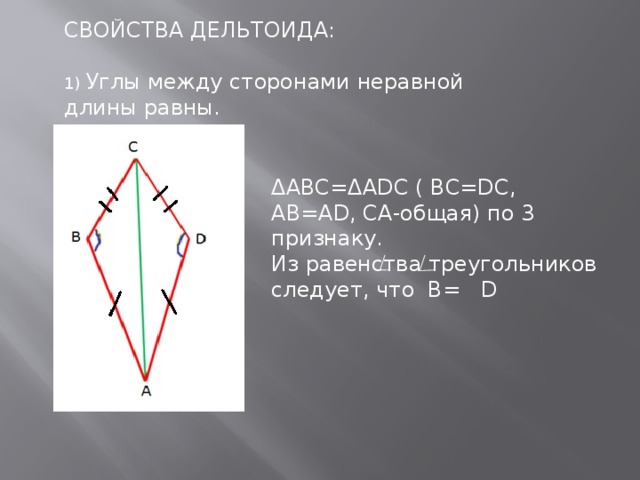
Таким образом, в ходе исследования выведены следующие свойства:
В выпуклом дельтоиде углы между сторонами неравной длины равны.
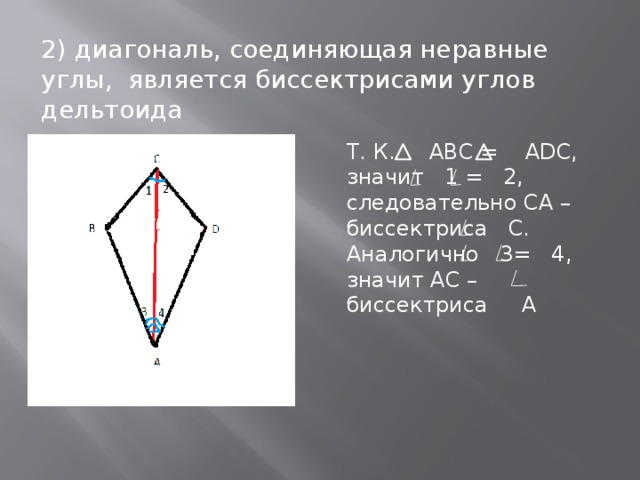
Диагонали являются биссектрисами углов дельтоида.
Диагонали выпуклого дельтоида взаимно перпендикулярны и при пересечении диагоналей, диагональ, соединяющая вершины равных углов, делится пополам.
В любой выпуклый дельтоид можно вписать окружность.
Признаки выпуклого дельтоида.
Выясним, какими признаками обладают выпуклые дельтоиды.
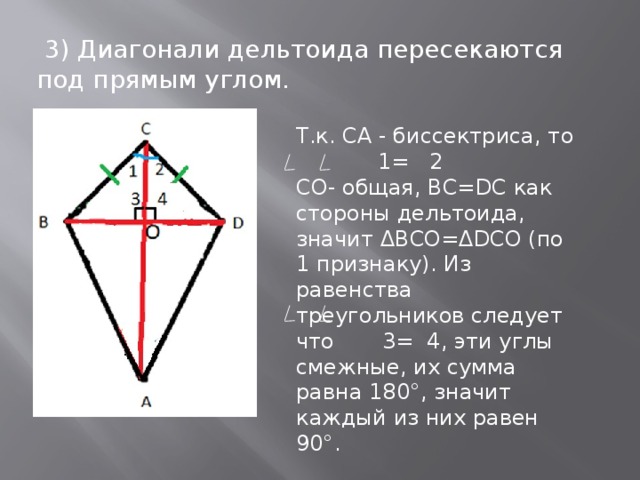
1) Выясним, что можно сказать о выпуклом четырёхугольнике, у которого диагонали пересекаются под прямым углом, и одна из диагоналей при этом делится пополам
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 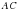 и
и  – диагонали данного четырехугольника,
– диагонали данного четырехугольника,  ,
, 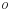 – точка пересечения диагоналей,
– точка пересечения диагоналей,  .
.
Исследуем этот четырёхугольник.
Рассмотрим 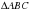 .
.
Диагональ  по условию. Согласно определения, перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
по условию. Согласно определения, перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
Отсюда следует, что 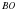 – высота.
– высота.
 – по условию. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Следовательно,
– по условию. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника. Следовательно, 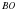 – медиана. Если в треугольнике высота одновременно является и медианой, то данный треугольник равнобедренный, то
– медиана. Если в треугольнике высота одновременно является и медианой, то данный треугольник равнобедренный, то 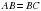 . Аналогично можно доказать, что треугольник
. Аналогично можно доказать, что треугольник  равнобедренный, а значит,
равнобедренный, а значит, 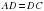 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан первый признак дельтоида: если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей при этом делится пополам, то данный четырёхугольник – дельтоид.
2) Исследуем выпуклый четырёхугольник  , у которого диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника. Напомним, что биссектриса угла – луч с началом в вершине угла, делящий угол на две равные части.
, у которого диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника. Напомним, что биссектриса угла – луч с началом в вершине угла, делящий угол на две равные части.
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 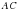 и
и  – диагонали данного четырехугольника,
– диагонали данного четырехугольника,  ,
, 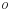 – точка пересечения диагоналей,
– точка пересечения диагоналей,  – биссектриса.
– биссектриса.
Исследуем данный четырехугольник.
Рассмотрим 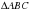 .
.
Так как  по условию, то
по условию, то 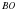 – высота.
– высота.
Так как  – биссектриса (по условию) и
– биссектриса (по условию) и 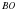 – высота, в треугольнике высота одновременно является и биссектрисой, то данный треугольник равнобедренный0, значит
– высота, в треугольнике высота одновременно является и биссектрисой, то данный треугольник равнобедренный0, значит 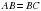 . Аналогично можно доказать, что
. Аналогично можно доказать, что  – равнобедренный, а это значит, что
– равнобедренный, а это значит, что 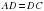 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан второй признак дельтоида: если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
3) Исследуем выпуклый четырёхугольник  , у которого одна из диагоналей – биссектриса двух равных углов этого четырёхугольника.
, у которого одна из диагоналей – биссектриса двух равных углов этого четырёхугольника.
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 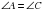 ,
, 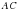 – биссектриса.
– биссектриса.
Исследуем данный четырехугольник.
Рассмотрим 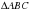 .
.
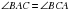 , так как это половинки равных углов
, так как это половинки равных углов  и
и  (
(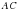 – биссектриса по условию). Если в треугольнике два угла равны, то он равнобедренный, значит
– биссектриса по условию). Если в треугольнике два угла равны, то он равнобедренный, значит 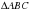 – равнобедренный, поэтому
– равнобедренный, поэтому 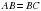 . Аналогично доказывается, что
. Аналогично доказывается, что  – равнобедренный, отсюда следует, что
– равнобедренный, отсюда следует, что 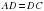 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан третий признак дельтоида: если в выпуклом четырёхугольнике одна из диагоналей – биссектриса двух равных углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
4) Исследуем выпуклый четырёхугольник  , у которого диагонали пересекаются под прямым углом, а две смежных стороны равны.
, у которого диагонали пересекаются под прямым углом, а две смежных стороны равны.
Дано:
 – выпуклый четырёхугольник;
– выпуклый четырёхугольник; 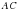 и
и  – диагонали данного четырехугольника,
– диагонали данного четырехугольника,  ,
, 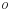 – точка пересечения диагоналей,
– точка пересечения диагоналей, 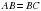 .
.
Исследуем данный четырехугольник.
Рассмотрим 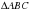 .
.
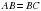 по условию, следовательно
по условию, следовательно 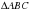 – равнобедренный по определению. Так как диагональ
– равнобедренный по определению. Так как диагональ  по условию, то
по условию, то 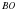 – высота, проведённая к основанию равнобедренного треугольника, следовательно
– высота, проведённая к основанию равнобедренного треугольника, следовательно 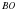 – медиана (по свойству высоты в равнобедренном треугольнике). Отсюда следует, что
– медиана (по свойству высоты в равнобедренном треугольнике). Отсюда следует, что  .
.
Рассмотрим 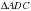 .
.
Так как 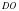 – высота, и
– высота, и  , следовательно,
, следовательно, 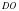 – медиана. Если высота в треугольнике является медианой, то он равнобедренный, значит
– медиана. Если высота в треугольнике является медианой, то он равнобедренный, значит 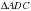 – равнобедренный,
– равнобедренный, 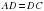 .
.
Вывод:  – дельтоид по определению.
– дельтоид по определению.
Итак, определен и доказан четвёртый признак дельтоида: если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, а две смежных стороны равны, то данный четырёхугольник – дельтоид.
Таким образом, в работе были определены и доказаны четыре признака дельтоида:
Если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей при этом делится пополам, то данный четырёхугольник – дельтоид.
Если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, и одна из диагоналей является биссектрисой углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
Если в выпуклом четырёхугольнике одна из диагоналей – биссектриса двух равных углов этого четырёхугольника, то данный четырёхугольник – дельтоид.
Если в выпуклом четырёхугольнике диагонали пересекаются под прямым углом, а две смежных стороны равны, то данный четырёхугольник – дельтоид.
Рассмотрим применение свойств и признаков дельтоида на практике (при решении задач).
ПРИМЕР. Задача: На стороне 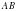 и
и  прямоугольника
прямоугольника  взяты т.
взяты т.  и т.
и т.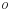 соответственно так, что
соответственно так, что  , а на стороне
, а на стороне  взята т.
взята т.  так, что
так, что  . Найти
. Найти  .
.
Дано:
 – прямоугольник
– прямоугольник


Найти: 
Решение:
 , так как это угол прямоугольника
, так как это угол прямоугольника
Рассмотрим четырёхугольник  .
.
 по условию;
по условию;  по условию
по условию
Вывод:  – дельтоид по определению.
– дельтоид по определению.
 – диагональ дельтоида, а так как диагонали дельтоида являются биссектрисами углов дельтоида, то
– диагональ дельтоида, а так как диагонали дельтоида являются биссектрисами углов дельтоида, то  .
.
Значит
Ответ:  .
.
Площади выпуклого дельтоида.
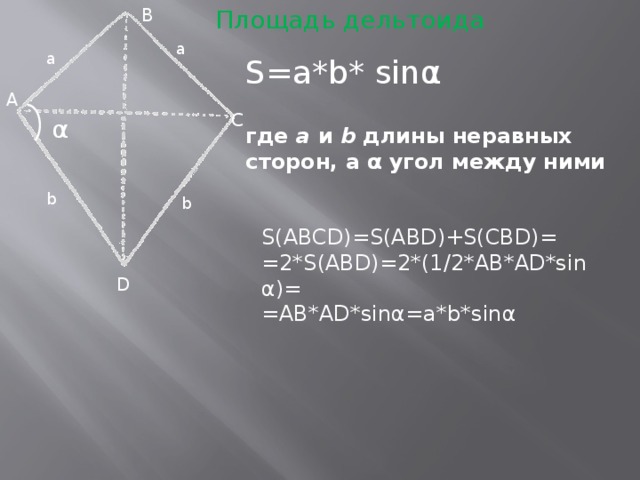
Площадь дельтоида также можно найти по формуле  , где
, где  и
и  длины неравных сторон, а α угол между ними. Докажем это.
длины неравных сторон, а α угол между ними. Докажем это.
Доказательство.
В выпуклом дельтоиде  проведём диагональ
проведём диагональ  , которая разделит его на два равных треугольника
, которая разделит его на два равных треугольника  и
и  (
( , по условию;
, по условию;  , по условию;
, по условию;  – общая), то есть площади этих треугольников равны. Площадь дельтоида
– общая), то есть площади этих треугольников равны. Площадь дельтоида  равна сумме площадей треугольников
равна сумме площадей треугольников  и
и  или 2 × S∆АВС. Площадь
или 2 × S∆АВС. Площадь  . Таким образом,
. Таким образом,  . А площадь любого дельтоида можно найти по формуле
. А площадь любого дельтоида можно найти по формуле  , где
, где  и
и  – неравные стороны дельтоида,
– неравные стороны дельтоида,  – угол между сторонами
– угол между сторонами  и
и  .
.
Выведем другие формулы нахождения площади основания дельтоидного многогранника, то есть площади выпуклого дельтоида.
Для этого рассмотрим выпуклый дельтоид  , у которого
, у которого  ,
,  (рис.9).
(рис.9).
Проведём диагональ  , которая разделит дельтоид на два треугольника
, которая разделит дельтоид на два треугольника  и
и  . Площадь дельтоида будет равна сумме площадей этих треугольников.
. Площадь дельтоида будет равна сумме площадей этих треугольников.
Рассмотрим треугольники  и
и  . Они равнобедренные, так как
. Они равнобедренные, так как  ,
,  по условию (равнобедренным называется треугольник, у которого две стороны равны).
по условию (равнобедренным называется треугольник, у которого две стороны равны).
Известно, что площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Таким образом площади  и
и  равны
равны  и
и  соответственно. А так как
соответственно. А так как  ,
,  по условию, то площади
по условию, то площади  и
и  равны
равны  и
и  соответственно. Тогда площадь дельтоида
соответственно. Тогда площадь дельтоида  будет равна .
будет равна .
Найдем площадь выпуклого дельтоида используя формулу Герона.
Площади треугольников 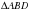 и
и  также можно найти по формуле Герона:
также можно найти по формуле Герона:
 , где
, где  ,
,  ,
, ,
,  – стороны треугольника.
– стороны треугольника.
Пусть в  и
и 
 ,
,  ,
,  .
.
Тогда 
 ;
;
Аналогично  ,
,  . Таким образом, площадь дельтоида равна .
. Таким образом, площадь дельтоида равна .
Таким образом, в ходе исследования выведены и доказаны формулы нахождения площади выпуклого дельтоида:
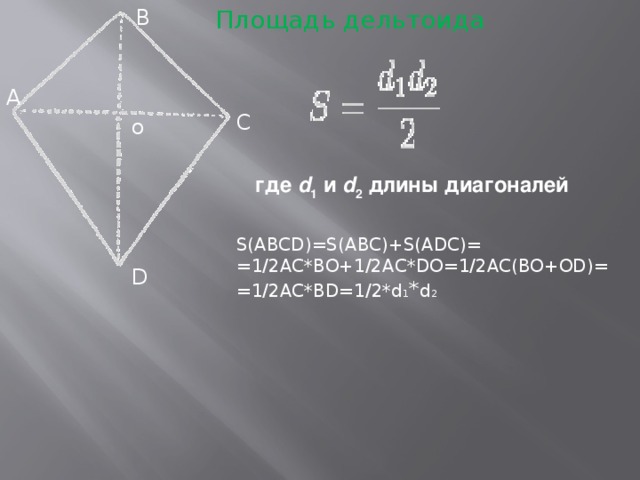
Площадь дельтоида равна половине произведения его диагоналей.
 , где
, где  и
и  – длины неравных сторон, а α угол между ними.
– длины неравных сторон, а α угол между ними.
, где  – диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания,
– диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания,  и
и  – неравные стороны основания.
– неравные стороны основания.
 , где
, где  и
и  – неравные стороны выпуклого дельтоида; α и β – углы дельтоида, лежащие между его равными сторонами.
– неравные стороны выпуклого дельтоида; α и β – углы дельтоида, лежащие между его равными сторонами.
Площади боковой и полной поверхности,
объем выпуклого дельтоидного многогранника.
Выясним, чему равен объём дельтоидного многогранника. Напомним, что объём — вместимость геометрического тела, т. е. части пространства, ограниченной одной или несколькими замкнутыми поверхностями.
Выведем формулу для нахождения объёма дельтоидного многогранника.
Основанием дельтоидного многогранника является дельтоид (смотрите выше). Площадь дельтоида равна половине произведения его диагоналей. Таким образом, объём дельтоидного многогранника равен половине произведения диагоналей его основания на высоту этого дельтоидного многогранника:  , где
, где  и
и  – диагонали основания дельтоидного многогранника,
– диагонали основания дельтоидного многогранника,  – его высота. Докажем это.
– его высота. Докажем это.
Рассмотрим дельтоидный многогранник  .
.
Проведём диагональ  , условно разделив данный многогранник на два многогранника:
, условно разделив данный многогранник на два многогранника:  и
и  ). Достроим многогранник
). Достроим многогранник  до параллелепипеда
до параллелепипеда  (призмы, основанием которой служит параллелограмм).
(призмы, основанием которой служит параллелограмм).
Для этого проведём параллельный отрезку  отрезок
отрезок  , параллельный отрезку
, параллельный отрезку  отрезок
отрезок  , отрезки
, отрезки  и
и  параллельные
параллельные  и
и  соответственно. Соединим точки
соответственно. Соединим точки  и
и  (рис.13) (см. Приложение). Получившийся параллелепипед будет состоять из двух равных многогранников
(рис.13) (см. Приложение). Получившийся параллелепипед будет состоять из двух равных многогранников  и
и  . Докажем это. Согласно определению, у параллелепипеда основаниями являются параллелограммы. Если мы проведём диагонали
. Докажем это. Согласно определению, у параллелепипеда основаниями являются параллелограммы. Если мы проведём диагонали  и
и  оснований
оснований
 и
и  соответственно, то разделим каждое основание на два равных треугольника
соответственно, то разделим каждое основание на два равных треугольника и
и  (
( , так как противоположные углы параллелограмма равны,
, так как противоположные углы параллелограмма равны,  и
и  , так как противоположные стороны параллелограмма равны =
, так как противоположные стороны параллелограмма равны =  по двум сторонам и углу между ними). Аналогично равны
по двум сторонам и углу между ними). Аналогично равны  . Согласно свойству параллелепипеда, его противолежащие грани параллельны и равны. Следовательно,
. Согласно свойству параллелепипеда, его противолежащие грани параллельны и равны. Следовательно,  ,
,  . Известно, что две фигуры называются конгруэнтными, или равными, если существует изометрия плоскости, которая переводит одну в другую. Другими словами, если основания и боковые грани одного многогранника равны основаниям и граням другого, то такие многогранники равны. Вывод: многогранники
. Известно, что две фигуры называются конгруэнтными, или равными, если существует изометрия плоскости, которая переводит одну в другую. Другими словами, если основания и боковые грани одного многогранника равны основаниям и граням другого, то такие многогранники равны. Вывод: многогранники  и
и  равны, то есть параллелепипед
равны, то есть параллелепипед  состоит из двух равных многогранников, один из которых является частью дельтоидного многогранника
состоит из двух равных многогранников, один из которых является частью дельтоидного многогранника  . Известно, что объём параллелепипеда равен произведению площади основания на высоту . А так как многогранник
. Известно, что объём параллелепипеда равен произведению площади основания на высоту . А так как многогранник  – это половина параллелепипеда
– это половина параллелепипеда  (смотрите выше), то соответственно и объём многогранника
(смотрите выше), то соответственно и объём многогранника  равен половине объёма параллелепипеда, то есть половине произведения площади основания параллелепипеда на высоту. А так как основание параллелепипеда – это параллелограмм, то половина площади параллелограмма
равен половине объёма параллелепипеда, то есть половине произведения площади основания параллелепипеда на высоту. А так как основание параллелепипеда – это параллелограмм, то половина площади параллелограмма  – это площадь
– это площадь  (площадь треугольника равна половине произведения основания на проведённую к нему высоту). Таким образом, объём многогранника
(площадь треугольника равна половине произведения основания на проведённую к нему высоту). Таким образом, объём многогранника  равен половине произведения основания на высоту. Аналогично можно найти объём многогранника
равен половине произведения основания на высоту. Аналогично можно найти объём многогранника  (второй половины дельтоидного многогранника
(второй половины дельтоидного многогранника  ). Известно, что если геометрическое тело составлено из геометрических тел, не имеющих общих внутренних точек, то объем данного тела равен сумме объемов тел его составляющих. Таким образом, мы можем говорить о том, что объём любого дельтоидного многогранника равен сумме объёмов частей, на которые делится этот многогранник его диагональю (отрезком, соединяющим две вершины дельтоидного многогранника, не принадлежащим одной грани). Найдя, объём каждой такой части и сложив полученные значения, мы найдём объём дельтоидного многогранника.
). Известно, что если геометрическое тело составлено из геометрических тел, не имеющих общих внутренних точек, то объем данного тела равен сумме объемов тел его составляющих. Таким образом, мы можем говорить о том, что объём любого дельтоидного многогранника равен сумме объёмов частей, на которые делится этот многогранник его диагональю (отрезком, соединяющим две вершины дельтоидного многогранника, не принадлежащим одной грани). Найдя, объём каждой такой части и сложив полученные значения, мы найдём объём дельтоидного многогранника.
Дано: дельтоидный многогранник  .
.
Найти:  -?
-?
Решение:
Проведём диагональ  , которая разделит данный многогранник
, которая разделит данный многогранник  на два многогранника:
на два многогранника:  и
и  (рис.14) (см. Приложение).
(рис.14) (см. Приложение).
Вывод: , где и
и  – диагонали основания дельтоидного многогранника
– диагонали основания дельтоидного многогранника  .
.
Так как, площадь дельтоида также можно найти по формуле  , где
, где  и
и  длины неравных сторон, а α угол между ними, то
длины неравных сторон, а α угол между ними, то  .
.
Таким образом, объём дельтоидного многогранника равен произведению двух неравных сторон его основания, умноженному на синус угла между ними, на высоту дельтоидного многогранника:  , где – высота дельтоидного многогранника.
, где – высота дельтоидного многогранника.  и
и  длины неравных сторон, α угол между ними,
длины неравных сторон, α угол между ними, 
Так как, основанием дельтоидного многогранника является выпуклый дельтоид и его площадь равна  (доказательство выше), то объём дельтоидного многогранника равен
(доказательство выше), то объём дельтоидного многогранника равен  , где
, где  и
и  – неравные стороны основания; α и β – основания, лежащие между его равными сторонами;
– неравные стороны основания; α и β – основания, лежащие между его равными сторонами;  – высота дельтоидного многогранника.
– высота дельтоидного многогранника.
Так как, площадь основания дельтоидного многогранника равна , то объем этого многогранника равен , где  – диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания,
– диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания,  и
и  – неравные стороны основания,
– неравные стороны основания,  – высота дельтоидного многогранника.
– высота дельтоидного многогранника.
Для нахождения площади полной поверхности (объединения оснований и боковой поверхности) дельтоидного многогранника достаточно сложить значения площадей всех его граней. Рассмотрим грани дельтоидного многогранника.
Основания являются равными дельтоидами (смотрите выше).
Боковые грани, рёбра которых являются равными сторонами основания дельтоидного многогранника, равны. Докажем это на примере дельтоидного многогранника  (рис.15).
(рис.15).
Рассмотрим боковые грани  и
и  .
.
 и
и  – параллелограммы, (смотрите выше);
– параллелограммы, (смотрите выше);
 , смотрите выше;
, смотрите выше;
 , как противолежащие стороны параллелограмма (противоположные стороны параллелограмма равны);
, как противолежащие стороны параллелограмма (противоположные стороны параллелограмма равны);
 , как противолежащие стороны параллелограмма.
, как противолежащие стороны параллелограмма.
Вывод:  .
.
Аналогично доказывается равенство боковых граней  .
.
Таким образом, для нахождения площади полной поверхности дельтоидного многогранника достаточно знать площади его боковых граней, рёбра которых являются неравными сторонами этого дельтоидного многогранника, и площадь основания. Сложив значения площадей каждой такой боковой грани и площади основания и умножив сумму этих площадей на два, мы получим значение площади полной поверхности дельтоидного многогранника. Для нахождения площади боковой поверхности дельтоидного многогранника нужно сложить значения площадей боковых граней, рёбра которых являются неравными сторонами основания, и умножить полученную сумму площадей на два.
Проведём диагональ дельтоидного многогранника из вершины его основания, являющийся общей для равных сторон этого основания. На рисунке это диагональ  . Докажем, что эта диагональ делит дельтоидный многогранник
. Докажем, что эта диагональ делит дельтоидный многогранник  , у которого
, у которого  и
и  , на два равных многогранника
, на два равных многогранника  и
и  . Рассмотрим
. Рассмотрим  и
и  .
.
Вывод:  по трём сторонам;
по трём сторонам;  по трём сторонам.
по трём сторонам.
Вывод:  .
.
Итак мы доказали, что диагональ дельтоидного многогранника, проведённая из вершины основания, являющейся общей для его равных сторон, делит дельтоидный многогранник на два равных многогранника.
Рассмотрим прямой дельтоидный многогранник.
В прямом дельтоидном многограннике все боковые рёбра перпендикулярны основанию (смотрите выше). А так как высота - отрезок, соединяющий основания многогранника и перпендикулярный им, то боковые рёбра прямого дельтоидного многогранника являются также его высотой. Объём дельтоидного многогранника равен произведению площади его основания на высоту этого дельтоидного многогранника (смотрите выше). Значит, объём прямого дельтоидного многогранника равен произведению площади его основания на боковую грань.
Известно, что площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы. А так как дельтоидный многогранник – призма по определению (смотрите выше), то площадь боковой поверхности прямого дельтоидного многогранника равна произведению периметра его основания на высоту дельтоидного многогранника.
Таким образом, в ходе исследования выпуклого дельтоидного многогранника дано определение дельтоидного многогранника, установлены правила его построения, определены его виды, выведены следующие свойства:
Основаниями дельтоидного образования являются выпуклые дельтоиды.
Боковые грани являются параллелограммами.
Объём дельтоидного многогранника равен половине произведения диагоналей его основания на высоту этого дельтоидного многогранника:  , где
, где и
и  – диагонали основания дельтоидного многогранника,
– диагонали основания дельтоидного многогранника,  – его высота.
– его высота.
Объём дельтоидного многогранника равен произведению двух неравных сторон его основания, умноженному на синус угла между ними, на высоту дельтоидного многогранника:  , где
, где  и
и  длины неравных сторон, α угол между ними,
длины неравных сторон, α угол между ними,  – высота дельтоидного многогранника.
– высота дельтоидного многогранника.
, где  и
и  – неравные стороны выпуклого дельтоида; α и β – углы дельтоида, лежащие между его равными сторонами;
– неравные стороны выпуклого дельтоида; α и β – углы дельтоида, лежащие между его равными сторонами;  – высота дельтоидного многогранника.
– высота дельтоидного многогранника.
, где  – диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания, - неравные стороны основания,
– диагональ основания дельтоидного многогранника, соединяющая общие вершины неравных сторон основания, - неравные стороны основания, 
 высота дельтоидного многогранника.
высота дельтоидного многогранника.
Для нахождения площади полной поверхности дельтоидного многогранника нужно сложить площади его боковых граней, рёбра которых являются неравными сторонами этого дельтоидного многогранника, с площадью основания, и умножить полученную сумму на два.
Для нахождения площади боковой поверхности дельтоидного многогранника нужно сложить значения площадей боковых граней, рёбра которых являются неравными сторонами основания, и умножить полученную сумму площадей на два.
Диагональ дельтоидного многогранника, проведённая из вершины основания, являющейся общей для его равных сторон, делит дельтоидный многогранник на два равных многогранника.
Объём прямого дельтоидного многогранника равен произведению площади его основания на боковую грань.
Площадь боковой поверхности прямого дельтоидного многогранника равна произведению периметра его основания на высоту.
Таким образом, цель исследовательской работы выполнена.
ЗАКЛЮЧЕНИЕ
Таким образом, в процессе исследований были даны определения выпуклого дельтоида и выпуклого дельтоидного многогранника, изложены их свойства, доказаны признаки, выведены и доказаны формулы нахождения площади выпуклого дельтоида, объема выпуклого дельтоидного многогранника, площади полной и боковой поверхности.
В качестве направлений для дальнейших исследований предполагается рассмотреть свойства аналогичных фигур в планиметрии и стереометрии.
СПИСОК ЛИТЕРАТУРЫ
http://gazpromschool.by.ru/projects/geometry/tr/tr312_1a.htm
http://geometricheskie.narod.ru/3D/Vparallelepiped.html
http://dic.academic.ru/dic.nsf/business/8852
Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. Геометрия 7-9 классы.б Учебник. 15-е изд. М.:"Просвещение", 2005.
Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев «Геометрия 10-11 класс»; издательство «Просвещение», 1996.
О.В.Георгиевский. Начертательная геометрия ( сборник задач с решением типовых примеров). АСТ; Астрель, 2002.
Я.И. Пелерман. Занимательная алгебра, геометрия. Изд-во: Книга, 2005.



 , у которого
, у которого 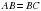 ,
, 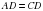 .
.  и рассмотрим треугольники
и рассмотрим треугольники 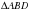 и
и 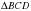 .
.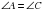 ,
, 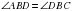 ,
, 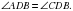 То есть в выпуклом дельтоиде углы между сторонами неравной длины равны и диагональ, соединяющая вершины неравных углов является биссектрисой (
То есть в выпуклом дельтоиде углы между сторонами неравной длины равны и диагональ, соединяющая вершины неравных углов является биссектрисой (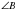 и
и 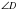 не могут быть равными, так как
не могут быть равными, так как 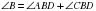 ,
,  , а
, а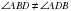 , так как это не углы при основании равнобедренного треугольника, аналогично
, так как это не углы при основании равнобедренного треугольника, аналогично 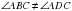 ).
). 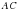 . Рассмотрим треугольники
. Рассмотрим треугольники 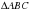 и
и 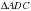 . Они равнобедренные по определению (треугольник называется равнобедренным, если у него две стороны равны0).
. Они равнобедренные по определению (треугольник называется равнобедренным, если у него две стороны равны0). 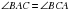 – так как это углы при основании равнобедренного треугольника.
– так как это углы при основании равнобедренного треугольника. 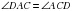 – так как это углы при основании равнобедренного треугольника.
– так как это углы при основании равнобедренного треугольника. 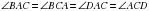 , следовательно
, следовательно 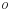 – точка пересечения диагоналей.
– точка пересечения диагоналей. 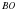 – отрезок биссектрисы
– отрезок биссектрисы  ).
). 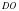 – отрезок биссектрисы
– отрезок биссектрисы 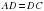 ,
, 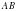 и
и  – противолежащие стороны,
– противолежащие стороны,