Выигрышная стратегия – урок информатики. 3-й класс
Тип урока – изучение нового материала.
Цели урока:
Обучающие – формирование знаний по теме “выигрышная стратегия”; учиться находить закономерность в ходе игры, формулировать и применять выигрышную стратегию (“секрет выигрыша”).
Развивающие – развивать интерес к данной теме и к предмету информатика в целом; развивать логическое мышление; расширять кругозор учащихся.
Воспитательные – способствовать формированию познавательного интереса как компонента учебной мотивации; способствовать развитию учебной и творческой активности учащихся.
Ход урока
Организационный момент. (2 мин.)
Проверка домашнего задания. (3 мин.)
- Какого вида первая закономерность? (расположение объектов в цепи)
- По каким правилам она построена? (количество точек и направление фигур).
- Какие правила расположения фигурок в таблице вы выделили? (в столбце – количество точек, в строке – направление).
- Как можно назвать таблицу слева по отношению к правой таблице? (аналогичная).
- В чем вы видите аналогию? (стрелки направлены так же и такого же цвета, как и фигурки в правой таблице).
Изучение нового материала. (13 мин.)
- Сегодня мы научимся не просто узнавать закономерности, но и применять их. (слайд 2)
Вы любите играть? А какие бывают игры? Чем отличаются и чем бывают похожи игры?
Люди придумали очень много разных игр: спортивных, настольных и т.д. Давайте поближе познакомимся с настольными играми. Эти игры можно разделить на два основных типа: игры, где всего два участника (соперника), например, нарды, и игры, в которых могут участвовать более двух игроков, например, лото.
Игры, в которых участвуют только два игрока тоже можно разделить на две группы. К первой группе относятся игры, где игроки делают ходы по очереди и обдумывают каждый ход, потому что он зависит от действий соперника (например, шашки, шахматы). Ко второй группе можно отнести игры, где ходы игроков никак не зависят от ходов противника (морской бой, игры с кубиком и фишками).
Обсуждение ответов учеников и разделение игр по типам:
играют только два игрока или возможно участие двух и более игроков; (например, шашки, шахматы, лото, домино, морской бой, нарды, игры с кубиком и фишками)
ходы игроков зависят от предыдущего хода соперника или нет (шашки, шахматы – морской бой, лото)
- Львенок и Черепаха решили сыграть в крестики-нолики. Черепаха ставила крестики, а Львенок – нолики.
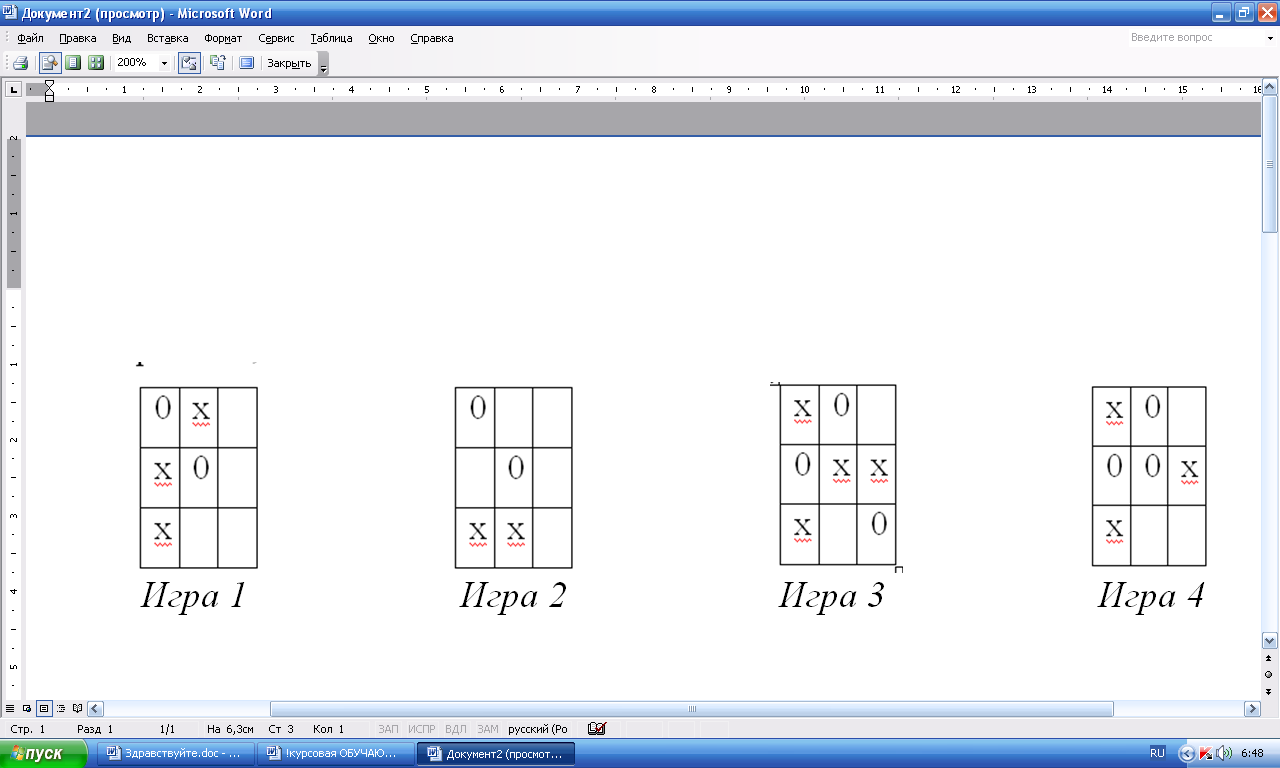
Рисунок 1. Заготовки для крестиков-ноликов
- Кто сколько ходов сделал? Чей ход следующий?
- Где Львенок должен поставить нолик, чтобы выиграть? (в первой игре – по диагонали).
- Как можно определить победителя второй игры? (выиграет тот, чей ход следующий).
- В третьей игре у соперников возникла проблема: они сделали уже по три хода, а победитель еще не определился. Кто победит в этой игре? (Никто, так как трех последовательных фигур уже не получится).
- Рассмотрите игру № 4. Кто выигрывает? (Львенок, так как ему осталось только поставить один нолик).
- Но следующий ход делает Черепаха… Представьте, что Черепаха попросила вас о помощи. В какой клетке нужно поставить ей крестик, чтобы помешать Львенку выиграть? (второй столбец, последняя строка).
- В каком случае в этой игре выиграет Черепаха? (Если Львенок ошибется в последнем ходе и поставит нолик в верхней строке, тогда у Черепахи будет три крестика в нижней строке).
- Что нужно знать. Чтобы выиграть в игре «Крестики-нолики»? (Как расположить фигуры, чтобы выиграть; как помешать выиграть сопернику?)
- Мы только что сформулировали выигрышную стратегию игры «Крестики-нолики».
Знакомство с понятием “стратегия игры”. (Слайд 3).
В ряде задач задается один и тот же вопрос: кто из двух игроков выиграет при правильной игре? Всегда ли выигрывает тот игрок, который начинает игру (или имеет 2-ой ход)?
Слова "правильная игра" означают, что если у кого-то из игроков есть стратегия, позволяющая выигрывать при любых ходах другого игрока, и он не делает "глупых" ходов, а стремится выиграть и следует своей выигрышной стратегии.
В каждой задаче необходимо придумать такую стратегию для одного из игроков.
Физминутка
Игра “Кто первым назовет число 100”. (Слайд 4).
В игре “Кто первым назовет число 100” участвуют двое. Один называет любое число от 1 до 9 включительно. Другой прибавляет к названному числу любое число от 1 до 9 и называет сумму. К этой сумме первый снова добавляет любое число от 1 до 9 и называет новую сумму. Выигрывает тот, кто назовет число 100. Кто выиграет при правильной игре?
Учащиеся читают условие игры и двое играют. Остальные слушают, если необходимо, дополняют или поправляют играющих, разгадывая секрет выигрыша в данной игре. (Выигрывает второй игрок, дополняя ходы первого игрока до круглого числа – 10, 20, 30 и т.д.)
Понятие “Выигрышная стратегия”. (Слайды 5, 6).
Разбор игры “Не больше двух предметов”. Поиск секрета выигрыша.
Многие простейшие игры имеют определенную закономерность и секрет выигрыша (выигрышную стратегию). В таких играх выигрышная стратегия зависит:
от правил (условий) игры;
от общего количества предметов, предложенных в игре;
от выбора игроком первого или второго хода.
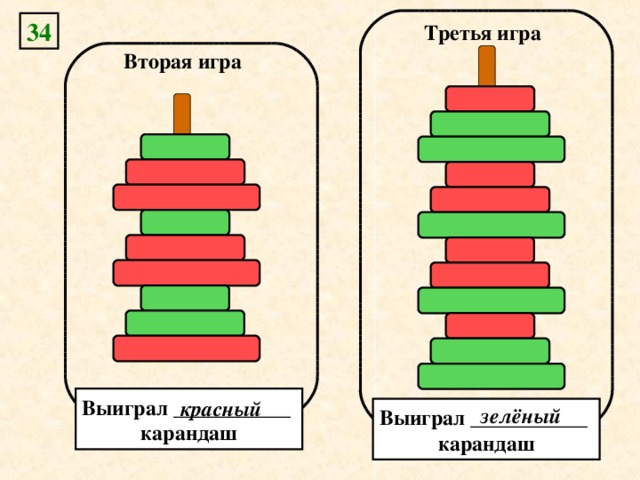
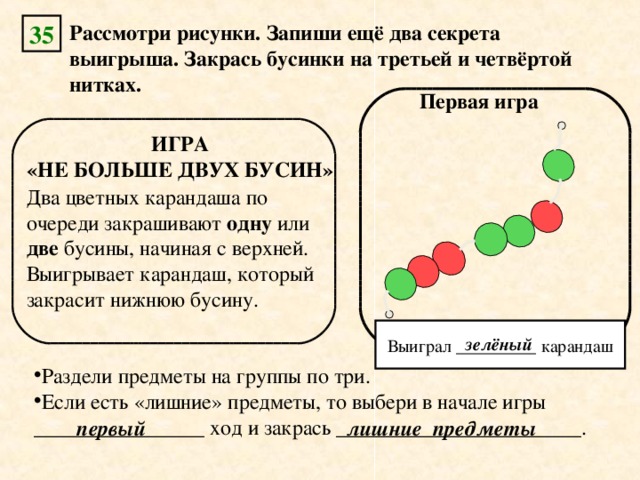
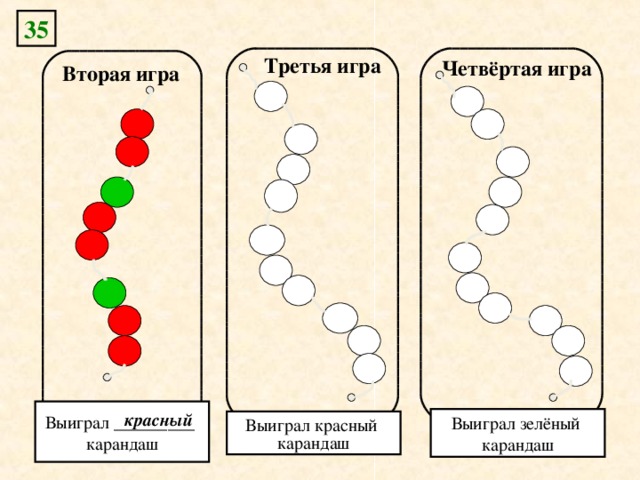
Рабочая тетрадь “Информатика в играх и задачах” 3 класс, ч.2 №№ 34, 35 (1, 2).
Формулировка “секрета выигрышной стратегии”. (Слайд 7).
Правила (секреты) выигрышной стратегии
Правило 1. Перед началом игры раздели все предметы на группы ОТ КОНЦА К НАЧАЛУ. Кол-во предметов в группе определяется условиями (не больше 2, тогда группы по 3, т.е. (n+1)). Самая первая группа может оказаться неполной – эти предметы мы называем “лишними”.
Правило 2. Если есть “лишние” предметы, то выбери 1-ый ход и закрась “лишние” предметы. Если нет “лишних” предметов – то выбери второй ход.
Правило 3. Дополняй ход другого игрока до (n+1) предмета, тогда в последней группе самый последний предмет будет твой.
5. Итог урока
Итак, мы сегодня с вами познакомились с очень интересным понятием “выигрышная стратегия”, которая используется в простейших играх с участием двух игроков.
6. Домашнее задание: рабочая тетрадь “Информатика в играх и задачах” 3 кл., ч.2 № 37.
Список литературы:
Горячев А.В., Горина К.И., Суворова Н.И. “Информатика в играх и задачах” 3 кл., ч.2., М. Баласс.
Информатика в играх и задачах. Методические рекомендации для учителя. 3 кл. Горячев А.В. и др., М., Баллас.