Разработка урока по теме: "Схемы. Практическая работа 10. Схемы, графы, деревья"

этап,
время

содержание урока

методы
обучения

средства
обучения

формы
обучения

1.
20 сек

Организация начала урока

Здравствуйте, ребята! Присаживайтесь. Меня зовут Олеся Александровна и я буду вести у вас уроки информатики.

Кто сегодня отсутствует?

Слово учителя

-

фронтальная

2.
3 мин

Актуализация знаний

Вспомните темы, изученные вами ранее. Можете открыть свои конспекты и учебники. Давайте повторим, что же такое электронная таблица?

Ответ учащихся: Электронная таблица – это программа для автоматической обработки числовых данных.

А какие примеры ЭТ вы можете привести?

Ответ учащихся: Microsoft Excel – файлы *.xls, *.xlsx

OpenOffice Calc – файлы *.ods – бесплатная

Хорошо, молодцы, а что же такое график?

Ответ учащихся: График служит для того, чтобы проследить за изменением нескольких величин при переходе от одной точки к другой.

Что такое диаграмма?

Ответ учащихся: Средство наглядного графического представления данных

И последний вопрос: Какие виды диаграмм вам уже известны?

Ответы учащихся: Круговые, кольцевые, точечные, линейные диаграмы, гистограмма.

Элемент беседы

Тетрадь, учебник

фронтальная

3.
2 мин

Постановка цели и задач урока

Ребята, мы переходим с вами к изучению новой темы. Она звучит так: «Схемы. Практическая работа 10. Схемы, графы, деревья». Сегодня мы с вами познакомимся с такими понятиями, как модель, информационная модель, граф, иерархия, иерархическая система, дерево. Научимся решать задачи с помощью графов и деревьев, а так же выполним практическую работу.

Как вы думаете, какая цель нашего занятия?

Ответы учащихся: познакомиться с графами, деревьями, узнать, что такое графы.

А какие задачи вы перед собой ставите? Маша, вот ты например?

Ответы учащихся: сформировать умения строить графы при решении задач, научиться строить графы и деревья

Хорошо, молодцы. Давайте запишем в тетрадях сегодняшнее число и тему.

Слово учителя, элемент беседы, запись в тетради

Презентация, тетрадь

Фронтальная

4.

1 мин

Физкультминутка

Слова данной игры заранее разучиваются с детьми. Ведущий поет вместе со всеми песню, по очереди показывая на те части тела, которые упоминаются:

Голова – голова;

Рамена – плечи;

Колена – колени;

Пальцы – щёлкает пальцами;

Очи – глаза;

Уши – уши;

Уста – губы;

Нос – нос

И постепенно увеличивает темп. Все движения идут под песню:

Голова – рамена – колена – пальцы,

Колена – пальцы – колена – пальцы,

Голова – рамена – пальцы,

Очи, уши, уста, нос.

5.

10 мин

Изучение нового материала. (теоретическая часть сопровождается показом презентации)

Ребята, скажите, а вы сталкивались со схемами в повседневной жизни?

Ответы учащихся. Да. Схемы проезда, схемы дома.

Верно. В повседневной жизни нас окружает множество разнообразных схем: схемы проезда, схемы дорожных развязок, схема метрополитена, схема расположения мест в зрительном зале, схема движения пригородных электропоездов и многое другое.

Схема — это представление некоторого объекта в общих, главных чертах с помощью условных обозначений. С помощью схемы может быть представлен и внешний вид объекта, и его структура.

Давайте посмотрим на экран и запишем определения.

Учащиеся записывают определения.

Например, внешний вид зрительного зала представлен на схеме, изображенной на рис. 2.21. Представление о внешнем виде квартиры можно получить по схеме на рис. 2.22. На рис. 2.23 представлена схема проезда в Бородино.

Обратите внимание на презентацию.

А скажите, для чего нам вообще нужны схемы?

Ответы учащихся. Они предназначены для того, чтобы у человека была возможность, например, выбрать подходящее место в зрительном зале, оценить размеры и расположение комнат будущей квартиры, разработать маршрут путешествия по Золотому кольцу, добраться до Бородинского поля и т. д.

Смотрим на презентацию и записываем определение.

Чертежи — условные графические изображения предметов с точным соотношением их размеров, получаемые методом проецирования, т.е. с сохранением масштаба. Рисунок содержит изображения, размерные числа, текст. Изображения дают представления о геометрической форме детали, числа — о величине детали и ее частей, надписи — о названии, масштабе, в котором выполнены изображения, материале, из которого изготовлена деталь.

Вы знакомы с блок-схемами — одним из наиболее наглядных способов записи алгоритмов; при этом используются следующие условные обозначения:

Последовательность действий указывается с помощью стрелок, соединяющих фигуры, обозначающие шаги алгоритма.

Запись в тетрадь со слайдов.

Есть ли у вас вопросы?

Учащиеся задают вопросы, учитель на них отвечает.

Следующее понятие, с которым мы познакомимся, это граф.

Как вы думаете, что это такое?

Учитель выслушивает ответы учеников и подытоживает.

Наглядным средством представления состава и структуры системы является граф.

Граф состоит из вершин, связанных линиями. Линия направленная (со стрелкой) называется дугой; линия ненаправленная (без стрелки) называется ребром. Линия, выходящая из некоторой вершины и входящая в нее же, называется петлей. Вершины могут изображаться кругами, овалами, точками, прямоугольниками и т. д.

Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями, то мы получим информационную модель рассматриваемой системы в форме графа.

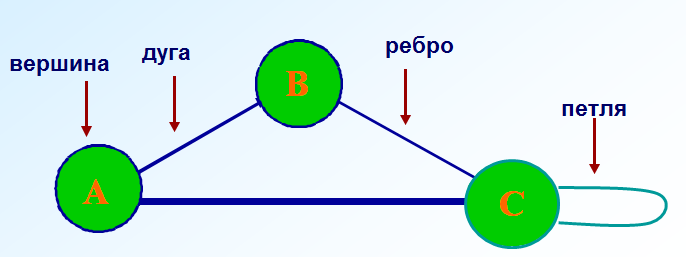
Обратите внимание на слайд.

Ранее мы рассматривали графы — схемы отношений, отражающие имеющиеся связи между объектами.

Например, граф, отражающий отношение «переписываются» между объектами класса «дети», может выглядеть, как показано на рис. 2.28.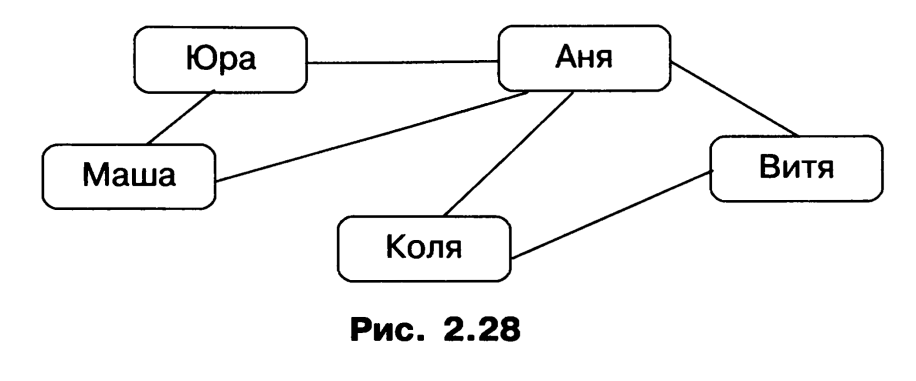

Отношение «переписываются» («пишут письма друг другу») является двухсторонним (симметричным). Поэтому соответствующие вершины соединены линиями без стрелок (ребрами).

Граф называется неориентированным, если его вершины соединены ребрами.

Путь по вершинам и ребрам графа, включающий любое ребро графа не более одного раза, называется цепью.

Пример цепи: Юра — Аня — Витя — Коля.

Цепь, начальная и конечная вершины которой совпадают, называется циклом.

Пример цикла: Аня — Коля — Витя — Аня.

Иначе выглядит граф, отражающий отношение «пишет письма» между теми же объектами класса «дети». Линии со стрелками (дуги) придают ему совершенно иной смысл (рис. 2.29).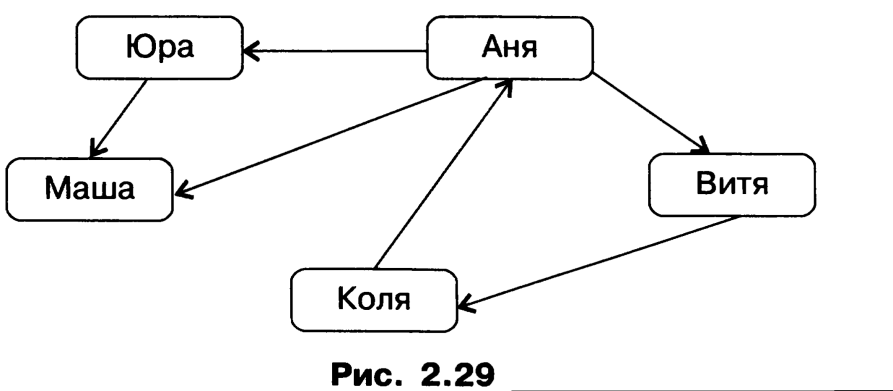

Граф называется ориентированным, если его вершины соединены дугами.

Граф называется взвешенным, если его вершины или ребра (дуги) характеризуются некоторой дополнительной информацией — весом вершины или ребра (дуги).

ВСЕ определения записываем в тетрадь.

Обратите внимание на экран.

На рис. 2.30 информация о городах Золотого кольца представлена взвешенным графом: веса его вершин — года основания городов, веса ребер — расстояния в километрах между городами.

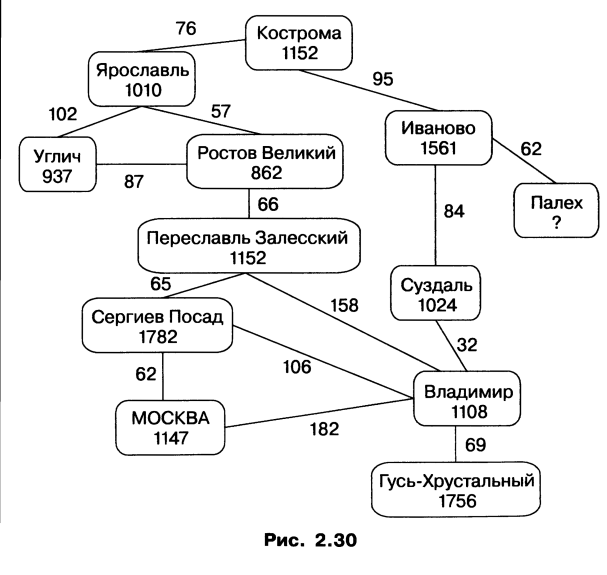
Граф с циклом называется сетью.

Ребята, есть ли у вас вопросы по этому блоку?

Ученики задают вопросы, учитель на них отвечает.

Мы переходим к следующей под теме «Деревья».

Иерархия — это расположение частей или элементов целого в порядке от высшего к низшему. Системы, элементы которых находятся в отношениях «является разновидностью», «входит в состав» и других отношениях подчиненности, называются иерархическими системами (системами с иерархической структурой).

Например, иерархическую структуру имеет школа, потому что в ней установлены следующие отношения подчиненности: директор — заместители директора — учителя — ученики.

Какие еще примеры иерархий вы можете привести?

Ответы учащихся: генеалогическое дерево, классификации.

Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.

Обычно у дерева, представляющего иерархическую систему, выделяется одна главная вершина, которая называется корнем дерева. Каждая вершина дерева (кроме корня) имеет только одного предка — обозначенный ею объект входит в один класс верхнего уровня. Любая вершина дерева может порождать несколько потомков — вершин, соответствующих классам нижнего уровня. Такой принцип связи называется «один ко многим». Вершины, не имеющие порожденных вершин, называются листьями.

Найти Web-страницу в Интернете можно с помощью адреса
Web-страницы.

Рисунок на доске. С изображением корня, предка и потомков.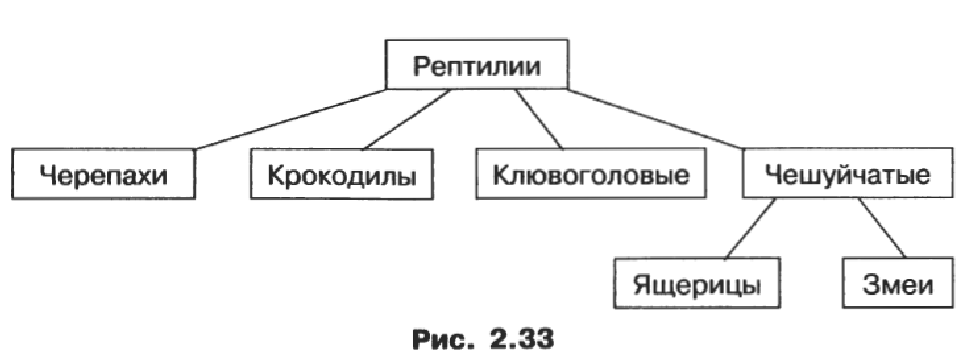

Назовите здесь корень, предков и потомков.

Для того чтобы найти файл в иерархической файловой структуре, можно указать путь к файлу. В путь к файлу входят записываемые через разделитель «\» логическое имя диска и последовательность имен вложенных друг в друга папок, в последней из которых находится нужный файл.

Например, пути к файлам на рис. 2.35 можно записать так:

С:\Проекты\История\

С:\Проекты\Информатика\

С:\Рисунки\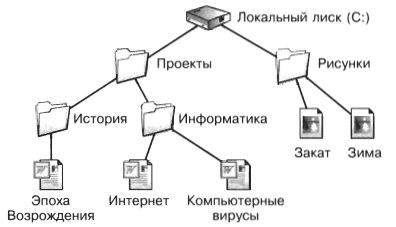

Напишите путь к файлу Закат.jpg

Использование графов при решении задач

Графы удобно использовать при решении некоторых классов задач.

Задача 1. Запись на доске.

Сколькими способами можно рассадить в ряд на три стула трех учеников? Выписать все возможные случаи.

Решение этой задачи удобнее всего представить в виде дерева. За его корневую вершину возьмем произвольную точку плоскости О.

На первый стул можно посадить любого из трех учеников — обозначим их А, В и С. На схеме это соответствует трем ветвям, исходящим из точки О: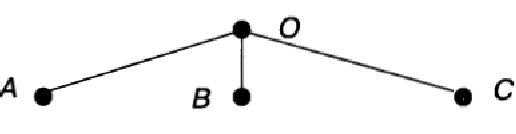

Посадив на первый стул ученика А, на второй стул можно посадить ученика В или С. Если же на первый стул сядет ученик В, то на второй можно посадить А или С. А если на первый стул сядет С, то на второй можно будет посадить А или В. Это соответствует на схеме двум ветвям, исходящим из каждой вершины первого уровня: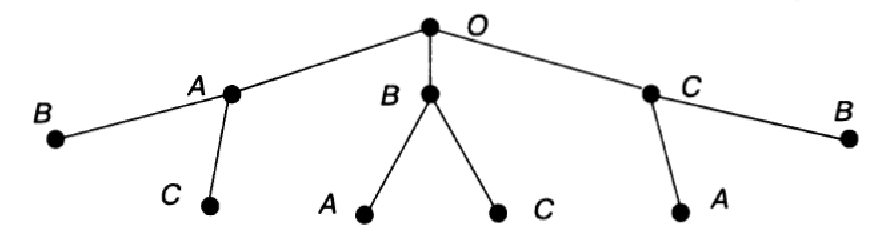

Очевидно, что третий стул в каждом случае займет оставшийся ученик. Это соответствует одной ветви дерева, которая «вырастает» на каждой из предыдущих ветвей.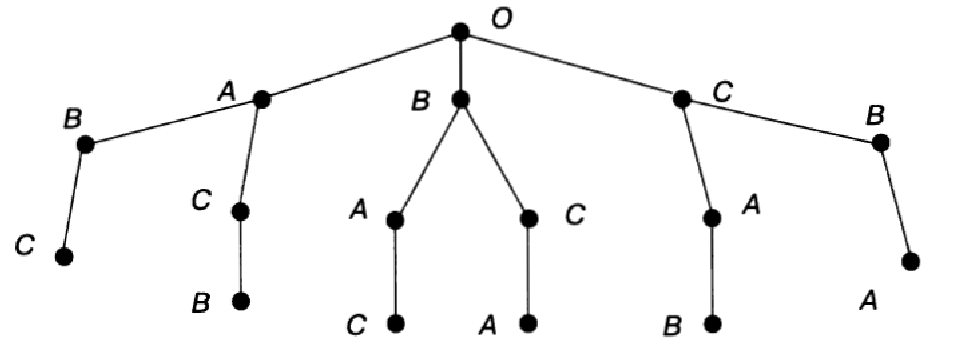

Выпишем все пути от вершин первого уровня к вершинам третьего уровня: А-В-С, А-С-В, В-А-С, В-С-А,С-А-В, С-В-А. Каждый из выписанных путей определяет один из вариантов рассаживания учеников на стулья. Так как других путей нет, то искомое число способов — 6.

Ребята, какие есть вопросы?

Проблемная ситуация. Ребята, давайте представим, что ваш друг никак не может понять, что такое схемы, графы и деревья. Как вы ему объясните это? (пара минут на подготовку инсценировки)

Слово учителя, элемент беседы

Запись в тетради

Элемент беседы

Запись в тетради

Слово учителя, элемент беседы

Слово учителя, запись в тетради

Элемент беседы

Слово учителя

Слово учителя

Запись в тетради

Слово учителя

Элемент беседы

Слово учителя

Элемент беседы

Слово учителя

Запись в тетради

Рисунок на доске

Элемент беседы

Самостоятельная работа

Решение задачи

Слово учителя

Элемент беседы

Кейс-метод

Презентация

Презентация, тетрадь

тетрадь

Презентация

Презентация

Тетрадь

Презентация

Презентация

Презентация

Презентация, тетрадь

Презентация

Презентация

Тетради

Презентация

Доска

Ответы учеников

Доска

Презентация доска

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Фронтальная

Групповая

6.

15 мин

Закрепление изученного материала. Практическая работа 10.

Присаживайтесь за компьютеры.

А сейчас мы с вами на практике закрепим знания, которые вы получили сегодня на уроке.

Присаживайтесь за компьютеры. Включайте их и открывайте папку с практическими работами.

У вас на столах есть листочки с практическими заданиями. Приступайте к выполнению. Если будут трудности – задавайте вопросы.

Практический

Раздаточный материал, ПК

Фронтальная

7.

2 мин

Подведение итогов урока.

Ребята, вы сегодня все успешно справились с заданием. Наш урок подходит к концу. Как вы считаете, мы выполнили цель, которую поставили в начале урока?

Ответ учащихся.

Выставление оценок за урок.

Слово учителя, элемент беседы

Фронтальная

8.

2 мин

Сообщение и объяснение домашнего задания.

Ваше домашнее задание написано на доске. Изучить конспект. Открываем дневники и записываем домашнее задание.

Всем большое спасибо за урок. Давайте поблагодарим друг друга аплодисментами. Вы свободны

Слово учителя, запись на доске

Фронтальная

9.

Рефлексия

Я вам предлагаю оценить сегодняшний урок. Я вам покажу 3 карточки, выберите для себя ту, которая соответствует вашему настроению в конце урока.

(«Три лица». Учитель показывает  учащимся карточки с изображением трех лиц: веселого, нейтрального и грустного.Учащимся предлагается выбрать рисунок, который соответствует их настроению.)

«Одним словом».
Закончите одним словом:
Сегодняшний урок – это…
Сегодня на уроке я …

Наглядный

Карточки

Фронтальная