Программные средства визуализации решений задач теории групп

Программные средства визуализации решений задач теории групп

Миняева Анна Геннадьевна МДИ-114

СИСТЕМА КОМПЬЮТЕРНОЙ АЛГЕБРЫ

G – Groups ( Группы )

A – Algorithms ( Алгоритмы )

P – Programming ( Программирование )

Основные центры разработки системы

Университет г.Сент-Эндрюс Университет штата Колорадо

Шотландия США

Ахен, Брауншвейг ( Германия)

Что такое GAP ?

Система компьютерной алгебры, спроектированная в 1985 году как инструмент комбинаторной теории групп – раздела алгебры, изучающего группы, заданные порождающими элементами и определяющими соотношениями

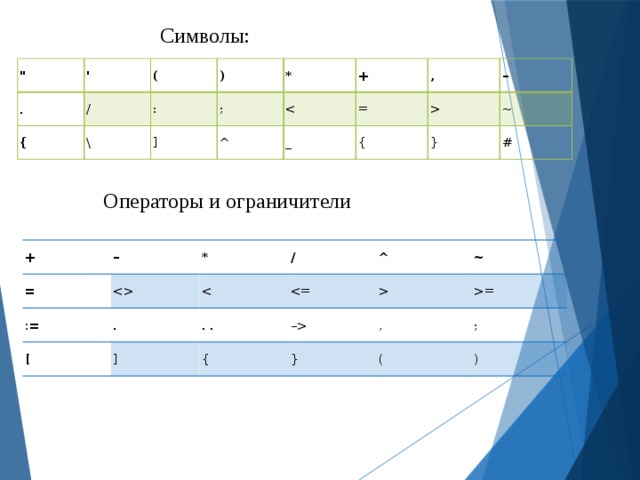  – { ~ } # Операторы и ограничители + = – := *   / [ . ^ . . ]   – ~ { , = } ; ( )" width="640"

Символы:

"

'

.

(

/

{

)

:

\

*

;

]

+

^

,

=

_

–

{

~

}

#

Операторы и ограничители

+

=

–

:=

*

/

[

.

^

. .

]

–

~

{

,

=

}

;

(

)

Ключевые слова:

and

do

for

not

elif

function

od

until

else

if

in

or

while

end

local

repeat

quit

fi

return

mod

then

Идентификаторы состоят из букв, цифр, символов «_», и должны содержать не менее одной

буквы или символа «_». При этом регистр является существенным.

Примеры идентификаторов:

A

Hello

100x

LongIdentifier

_100

HELLO

• Список некоторых групп из библиотеки системы GAP с

указанными в скобках командами обращения к этим группам, причём параметр filt в этих командах определяет способ задания группы. Например, при filt=IsPermGroup получаем подстановочное представление группы, а при filt = IsMatrixGroup — её линейное представление.

• Циклическая группа порядка n (CyclicGroup( [filt, ]n ));
• Абелева группа , разложимая в прямую сумму групп порядков

ints [1], ints [2],..., ints [ n ] для списка ints натуральных чисел (AbelianGroup( [filt,]ints ));

• Группа диэдра порядка n (DihedralGroup( [filt, ]n ));
• Знакопеременная группа степени deg (AlternatingGroup( [filt,]deg ));
• Симметрическая группа степени deg (SymmetricGroup( [filt, ]deg ));
• Группа Матье степени degree (MathieuGroup( [filt, ]degree ));

• Общая линейная группа обратимых d × d матриц над кольцом R (GL([filt, ]d, R ));
• Общая линейная группа обратимых d × d матриц над конечным полем из q элементов (GL( [filt, ]d, q ));
• Специальная линейная группа обратимых d × d матриц над кольцом R (SL( [filt, ]d, R ));
• Специальная линейная группа обратимых d × d матриц с единичным определителем над конечным полем из q элементов (SL( [filt, ]d, q ));
• Проективная специальная линейная группа , изоморфная фактор-группе группы SL ( d , q ) по её центру (PSL( [filt, ]d, q ));

GAP как калькулятор:

• gap (9 - 7) * (5 + 6);
• 22
• gap 2^64;
• 18446744073709551616

Разложение целого числа на множители

• gap FactorsInt(2^200-1);
• [3, 5, 5, 5, 11, 17, 31, 41, 101, 251, 401, 601, 1801,
• 4051, 8101, 61681, 268501, 340801, 2787601, 3173389601]

Работа с матрицами:

• Зададим матрицу А:
• gap A:=[[1,2,3,4],[4,2,1,5],[-1,10,0,0],[2,-4,7,0]];;
• Для ее удобочитаемого вывода на экран применяется команда  Display :
• gap Display(A);
• [ [ 1, 2, 3, 4 ],
• [ 4, 2, 1, 5 ],
• [ -1, 10, 0, 0 ],
• [ 2, -4, 7, 0 ] ]
• Вычислим определитель этой матрицы:
• gap DeterminantMat(A);
• -932

Симметрическая группа имеет, кроме себя самой и единичной подгруппы, лишь следующие нормальные подгруппы: а) знакопеременную группу U _4; б) «четверную группу Клейна». Последняя группа абелева.

Найти число Силовских 5-подгрупп в .