Принципы проведения вычислительного эксперимента. Модель, алгоритм, программа

Вычислительный эксперимент. Модель, алгоритм, программа

Выполнила: Ондар Тайгана, студентка группы МДИ-117

Вычислительный эксперимент

Основная идея вычислительного эксперимента – замена исходного объекта математической моделью и дальнейшее изучение модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов.

Суть вычислительного эксперимента состоит в том, что на основе различных вариантов математических моделей с помощью компьютера проводятся исследования свойств объекта, процесса или системы, находятся их оптимальные параметры, уточняется математическая модель.

Вычислительный эксперимент позволяет получать и к о лич е с тв е н ные ха р а к т е ри с т и к и ис с л е д у е м о г о о б ъ е к т а , я в л я е т ся

у т о чнять о р у д и е м

п о иска н е из в е с т ных к а ч е с т в е н н ых з а к о н о мерн о с т ей , п р и с у щ их и з у ч а е м ы м

объектам.

• Модель  (от лат. modulus — мера, образец) — упрощённое представление о реальном объекте, процессе или явлении.

• Алгоритм — это последовательность действий, которая направлена на достижение окончательного решения проблемы наиболее оптимальными и эффективными способами.

• Программа (от греч. programma — объявление, предписание) — понятие, обозначающее определенный способ организации сложных видов  деятельности,  который предполагает перспективное планирование, взаимодействие нескольких субъектов и учет многообразных внешних факторов.

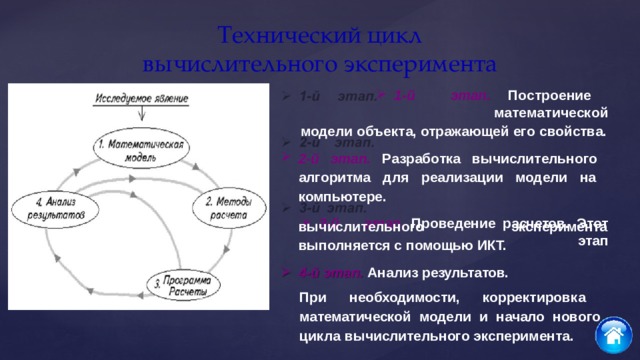
Технический цикл вычислительного эксперимента

• 1 - й э т ап . П о с т ро е н ие м а т е м а т и ч е с к ой

модели объекта, отражающей его свойства.

• 2-й этап. Разработка вычислительного алгоритма для реализации модели на компьютере.

• 3-й этап. Проведение расчетов. Этот этап

вычислительного

выполняется с помощью ИКТ.

• 4-й этап. Анализ результатов.

эксперимента

При необходимости, корректировка математической модели и начало нового цикла вычислительного эксперимента.

Возможности вычислительного эксперимента

• Организация творческой, исследовательской деятельности учащихся.
• Реализация связи теории с практикой (основой вычислительного эксперимента является математическое моделирование, геометрической базой – прикладная математика).
• Изучение этапов математического моделирования: постановка проблемы и ее

анализ , п о с т р оение м а т ем а т и ч е с к ой м о д е ли , исс л едо в а н и е м о де л и, решения.

• Формирование алгоритмической культуры учащихся.
• Визуализация учебной информации, представление ее в виде графиков;

и з у ч е н и е

• Р а с с м о т р е н ие м а т е м а т и ч е ск их о б ъе к т ов в д и нам и к е , илл ю с т рация про ц е с с а изменения объектов с изменением значений параметров.
• Пред о с т а в л ен и е и н ф о р м ац и и п о исп о ль з о в а н ию в о з м о жн о с т е й прогр а м мы при решении математических задач вне школьных занятий.

Программные комплексы

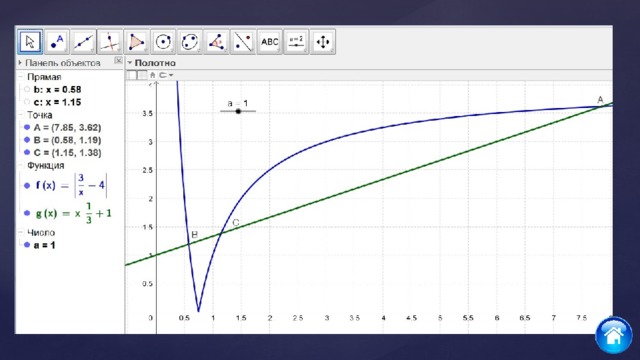
• MS Excel – табличный процессор, позволяющий строить графики и диаграммы, решать экономические задачи и задачи с параметром путем варьирования значений переменных;

• GeoGebra – динамическая геометрическая

сред а с шир о к и м и построения и

стереометрических фигур и поверхностей, решения уравнений, неравенств и их систем, решения геометрических задач, а также задач теории вероятностей и математической статистики, прикладных задач;

ис с л едо в а н ия гр а ф и ко в ,

в о з м о ж н о с т ям и для

• MathCAD Prime 3.0 – система компьютерной алгебры из класса систем автоматизированного проектирования. Содержит сотни операторов и встроенных функций для решения различных технических задач. Среди возможностей MathCAD можно выделить:

• решение различных уравнений и систем, в том числе и численными методами;

• п о с т роение д в у мерных, т рёх м е р ных

гр а ф и ко в

ф у н к ц и й, гр а ф и к ов в п о л я рной

с ис т е ме

координат, контурных и векторных графиков;

• в ы п о лне ни е в ы ч и с л е ни й в с им в о льн о м р е ж и ме для преобразования и упрощения выражений, а

также решения задач в общем виде;

• выполнение операций с векторами и матрицами;
• аппроксимация кривых;
• проведение статистических расчётов и работа с

распределением вероятностей.

• К о м пас 3D L T – с и с т е м а автоматизированного п р ое к т и р о в а н ия, п р едн а зн а чен н ая для создания трёхмерных моделей о б ъ е к т о в , и н ж ен ерных де т а л е й и со о р у ж е н и й . Мно г о ч ис л е н ные се р висные ф у н к ции о б л е гч а ю т ре ш ени е в сп о м ог а т ел ь ных з ад а ч п р ое к т и р о в а н ия и о б с л уж и в а ния п р оиз в о д с тв а . Р а зра б о т а н ные компьютерные модели могут быть реа л и з о в а ны с и сп о ль з о в а н и е м т е х н о л о г ии 3 D -п е ч а т и с ц е л ь ю их дальнейшего исследования.

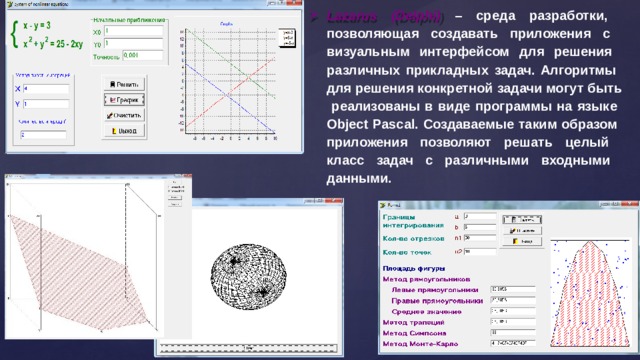
• Lazarus (Delphi) – среда разработки, позволяющая создавать приложения с визуальным интерфейсом для решения различных прикладных задач. Алгоритмы для решения конкретной задачи могут быть реализованы в виде программы на языке Object Pascal. Создаваемые таким образом приложения позволяют решать целый класс задач с различными входными данными.

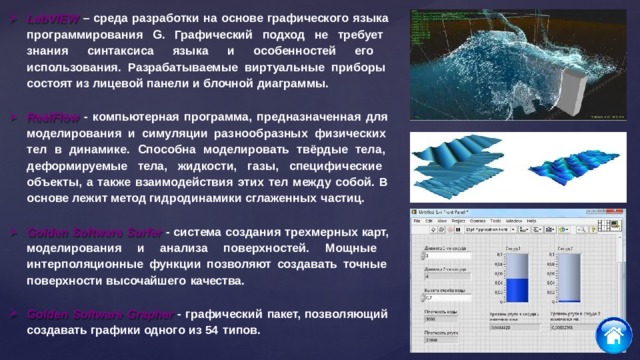
• LabVIEW – среда разработки на основе графического языка программирования G. Графический подход не требует знания синтаксиса языка и особенностей его использования. Разрабатываемые виртуальные приборы состоят из лицевой панели и блочной диаграммы.

• RealFlow - компьютерная программа, предназначенная для моделирования и симуляции разнообразных физических тел в динамике. Способна моделировать твёрдые тела, деформируемые тела, жидкости, газы, специфические объекты, а также взаимодействия этих тел между собой. В основе лежит метод гидродинамики сглаженных частиц.

• Golden Software Surfer - система создания трехмерных карт, моделирования и анализа поверхностей. Мощные интерполяционные функции позволяют создавать точные поверхности высочайшего качества.

• Golden Software Grapher - графический пакет, позволяющий создавать графики одного из 54 типов.

Задача 1. Решение уравнения с параметром.

• й этап. Построение модели. Зададим две функции f(x) и g(x), соответствующие левой и правой частям уравнения. Построим графики функций. Графики могут иметь или не иметь точки пересечения. Это зависит от значения параметра. Решение сводится к рассмотрению возможных вариантов расположения графиков.

• й этап. Разработка вычислительного алгоритма. Количество точек пересечения графиков определяет количество корней заданного уравнения. Оно может изменяться при изменении параметра. Для изменения параметра создадим Ползунок, используя соответствующий инструмент среды GeoGebra.

3-й этап. Проведение расчетов. Рассмотрим несколько возможных вариантов расположения графиков при изменении параметра. Определим значения параметра, при которых графики пересекаются более, чем в 2 точках.

4-й этап. Анализ результатов. Исследования поведения графика линейной функции g(x) при различных значениях параметра с шагом 0.01 показывают, что прямая имеет более двух точек пересечения с графиком функции f(x) при a  (0; 2.26)

Задача 2. Решение прикладной экономической задачи.

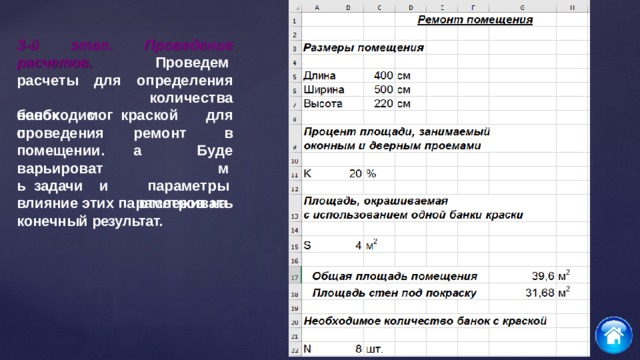
Комната имеет размеры A x B x C см, причем k% занимают оконный и дверной проемы. Необходимо рассчитать, какое количество краски потребуется для проведения ремонтных работ в комнате, если с помощью 1 банки можно закрасить S м 2 ?

1-й этап. Построение модели. Для построения математической модели описанного процесса необходимо провести формализацию входных параметров:

• форма помещения – прямоугольная (A см – длина, B см – ширина, C см – высота);

• – процент окрашиваемой площади;

(1  k ) %

– площадь стен для покраски;



S пов  2  ( a  c  b  c )  (1  k )  2  c  ( a  b )  (1  k )

S







– необходимое количество банок с краской (целое число).

N  округл 



пов





S

2 - й эт ап . Разр а б от к а вычисли т е ль но г о а л г о р и т м а . Д л я про в е дения

м о де л и с

компьютерного эксперимента по построенной математической

помощью табличного процессора MS Excel необходимо построить соответствующую электронную таблицу, задав конкретные числовые значения параметрам задачи. Проведем расчеты полной площади помещения и площади стен под покраску по соответствующим формулам:

• G17 = 2*$C$7*($C$5+$C$6)/10000;
• G18 = =(2*$C$7*($C$5+$C$6)/10000)*(1-$B$11/100).
• Для округления полученного значения N в ячейке B22 до целого числа используем встроенную функцию ОКРУГЛ : B22 = ОКРУГЛ($G$18/$B$15;0).

П р о в е де ние Про в е д е м о п р е де л е н ия к о л и ч е с т в а

3-й этап. расчетов. ра с ч е т ы для н е о б х о д и м о г о

краской р е м он т а

д ля

банок с проведения помещении. в а рь и р о в а т ь задачи и

в

Б у д е м п а р ам е т ры от с л ежи в а т ь

влияние этих параметров на

конечный результат.

4-й этап. Анализ результатов. Полученный ответ удовлетворяет условию задачи и позволяет определить необходимое количество краски, а также установить взаимосвязь между исходными параметрами задачи. С помощью построенной электронной таблицы также возможно рассчитать количество краски для проведения

р е м о н т а в р а з лич н ых п о мещениях, а д о ба в ив параметры, можно определить и количество

доп о лн и т е л ь н ы е ино г о м а т ер и ал а

(например, обоев, клея, ламината, цемента и т.д.).

Задача 3. Доказательство теоремы.

Биссе к т р и с а т р еу г о л ь ника д ел и т п р о т и в о п о л о ж ную с т ор о н у пропорциональные прилежащим сторонам треугольника.

на отрезки,

1-й этап. Построение модели.

Средством утверждения на я в ля ю т с я : т о ч к а выведенные на

проверки справедливости

динамической модели

А С ,

Е – с е ре д ина

экран текущие

з н а че н ия

длин АВ и ВС. Перемещая вершину В, можно

доб и т ься

совмещения

т о чек Е и D . Уч - ся

вывод,

что

делают

утверждение

спр а в ед ли в о дл я рав н обедр е нн ы х треугольников, где АС является основанием.

В ходе экспериментов с моделью учащиеся могут установить, что отношение отрезков АD и DC как-то зависит от соотношения длин АВ и ВС, в частности, высказать эту гипотезу в терминах «больше/меньше», что побуждает их к дальнейшему исследованию закономерности.

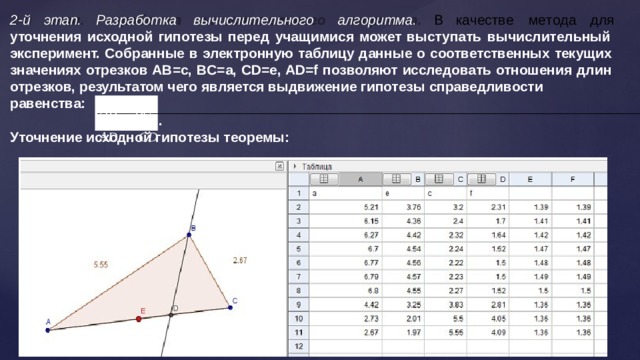
2 - й э т ап . Разра б о т к а выч и сли т е льно г о а л г ор и т м а . В к а ч е с т в е м е т о да для

уточнения исходной гипотезы перед учащимися может выступать вычислительный эксперимент. Собранные в электронную таблицу данные о соответственных текущих значениях отрезков АВ=c, BC=a, CD=e, AD=f позволяют исследовать отношения длин отрезков, результатом чего является выдвижение гипотезы справедливости

равенства:

AB  BC

AD CD

.

.

Уточнение исходной гипотезы теоремы:

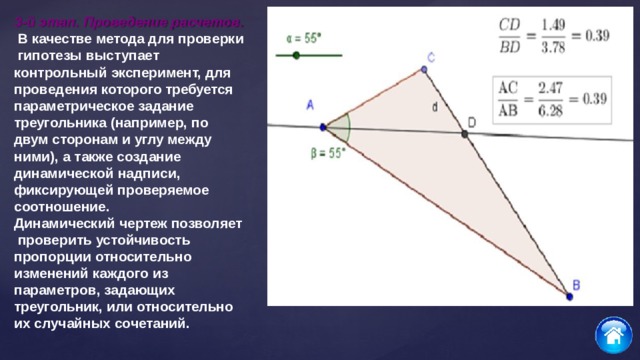
3-й этап. Проведение расчетов. В качестве метода для проверки гипотезы выступает контрольный эксперимент, для проведения которого требуется параметрическое задание треугольника (например, по двум сторонам и углу между ними), а также создание динамической надписи, фиксирующей проверяемое соотношение.

Динамический чертеж позволяет проверить устойчивость пропорции относительно изменений каждого из параметров, задающих треугольник, или относительно их случайных сочетаний.

4-й этап. Анализ результатов. В качестве метода для проверки гипотезы выступает модифицирующий эксперимент. Например, учащимся можно предложить задание: «Проверьте, выполняется ли утверждение, если биссектриса внешнего угла треугольника или ее продолжение пересекает продолжение противоположной стороны, то точка пересечения отстоит от концов этой стороны на расстояния, пропорциональные длинам двух других сторон».

Задача 4. Площадь фигуры, ограниченной линией.

1-й и 2-й этапы. Построение модели. Разработка вычислительного алгоритма. Для решения поставленной задачи необходимо воспользоваться геометрическим смыслом определенного интеграла. Для нахождения значения интеграла рассмотрим некоторые методы численного интегрирования, основная идея которых состоит в замене подынтегральной функции на более простую. При этом для оценки значения интеграла вычисляется значение подынтегральной функции в узловых точках. При замене подынтегральной функции на полином нулевой, первой и второй степени получаются соответственно методы прямоугольников, трапеций и Симпсона.

Метод прямоугольников:

 x  b  a ;

x 0 , x 1 ,..., x n

• Разделим отрезок [a;b] точками

на n равных отрезков длиной

n

y 0 , y 1 ,..., y n

– значения функции в точках

.

x 0 , x 1 ,..., x n

• Составим интегральные суммы

.

y 0  x  y 1  x  ...  y n  1  x

• Если функция положительная и возрастающая, то данная сумма приближенно равна значению

интеграла и выражает площадь фигуры, составленной из «входящих»

b  a n

b

 f ( x ) dx 

a

( y 0  y 1  ...  y n  1 )

прямоугольников.

b  a n

b

 f ( x ) dx 

a

( y 1  y 2  ...  y n )

При этом формула

выражает площадь ступенчатой фигуры,

составленной из «выходящих» прямоугольников.

• Чем меньше длина отрезков, на которые делится отрезок [a;b], тем точнее значение, вычисляемое по этой формуле, искомого интеграла.
• Более точное значение интеграла можно получить, если взять в качестве опорной точки для нахождения высоты, точку посередине промежутка.

Метод трапеций:

• Аналогично предыдущему методу разделим отрезок [a;b] точками на n произвольных отрезков.
• На каждом элементарном отрезке заменим (аппроксимируем) подынтегральную функцию на линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями.
• Сумма площадей полученных трапеций даст приближенное значение интеграла на отрезке [a;b].

b



a

n  1 f ( x )  f ( x )



i  0

( x i  1  x i )

f ( x ) dx 

i i  1

2

Метод Симпсона:

• Если для аппроксимации использовать многочлен второй степени, то на каждом из участков

отрезка [a; b] функция заменится на фрагмент параболы.

• Для аппроксимации можно использовать три точки – концы и середину отрезка. Приближенное

значение интеграла выражается формулой:

b

 f ( x ) dx 

a

b  a   a  b  

 f ( a )  4 f    f ( b ) 

2

6









Вероятностный метод Монте-Карло:

• «поместим» полученную фигуру в некоторую прямоугольную область;
• задавая случайным образом координаты точек, будем помещать их в пределах этой области;
• отношение числа точек, попавших внутрь фигуры, к общему числу точек примерно равно отношению площади фигуры к площади прямоугольника.

3-й э т а п. Про в е д е ние

ра с ч е т о в .

Описанные

м е т о ды

реализованы

в

P asca l .

я зык е

O b je c t

сред е Del p hi на

п о з в о л я е т

варьировать

Прогр ам м а некоторые

пар а м е т ры

эксперимента,

а

т а к ж е в и з у аль но пр о с л еди т ь з а е г о

ходом.

4-й этап. Анализ результатов.

Проведя компьютерный эксперимент с использованием выше перечисленных методов, можно оценить их точность, а также проследить зависимость получаемых результатов от количества отрезков, на которые разбивается интервал (или от количества точек).

Задача 5. Задача с экономическим содержанием.

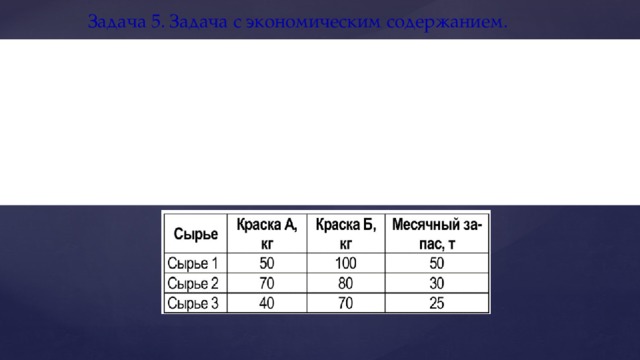
Предприятие имеет месячный цикл производства. Надо определить, сколько в месяц следует производить краски типа А и сколько – типа Б. Производственные мощности позволяют выпускать в месяц суммарно 500 т краски всех типов. Одна тонна краски А приносит в среднем 2000 руб. прибыли, а одна тонна краски Б – 2500 руб. Отдел маркетинга требует, чтобы краски типа А производилось не менее 200 т в месяц, поскольку есть договоры на такое количество, а краску типа Б нельзя производить более 150 т, поскольку большее количество трудно реализовать. На изготовление красок А и Б необходимо сырье трех видов согласно таблице:

Построение

производственной

модели

Дл я п о с т роения

мо д е л и.

1-й этап.

необходимо

программы

опр е де л и т ь

производственный

п лан , прин о ся щ ий

максимальную

прибыль, т.е. найти максимум функции Z = 2000x 1 + 2500x 2 при

выполнении ограничений: общее количество краски типов А и Б не должно превышать 500 т; произведенное количество краски А должно быть не меньше 200 т, а краски Б – не более 150т.

В таблице показано, сколько и какого сырья необходимо для производства одной тонны краски А и одной тонны краски Б, величины месячных запасов сырья. Общее количество используемого сырья не должно превышать их месячные запасы. Таким образом, имеем еще три ограничения – по одному для каждого типа сырья.

2-й этап. Разработка вычислительного алгоритма. По условию задачи:

Необходимо найти максимальное значение целевой функции при выполнении ограничений. Для нахождения корректного решения имеет смысл добавить условие неотрицательности для x 2 (x 2 ≥0).

3-й этап. Проведение расчетов. Решение задачи в системе компьютерной алгебры Mathematica без использования программирования. Для решения достаточно из условия задачи записать целевую функцию (Z), ограничения (G), указать переменные

(V) и выполнить команду NMaximize[{Z,G},V]. В результате на экране мы увидим:

4-й этап.

Ан а лиз

результатов.

Полученный

о т в ет

удовлетворяет

условию задачи и показывает, что при выпуске 257,143 т краски типа А и 150 т краски типа Б предприятие получит максимальную прибыль 889 286 руб.

Задача 6. Решение прикладной задачи по физике.

В двух сообщающихся сосудах находится ртуть. Диаметр первого сосуда в четыре раза больше диаметра второго. В первый сосуд наливают воду. Высота столба воды 0,7 м. Определить, на сколько поднимется уровень ртути в одном сосуде и опустится в другом.

1-й этап. Построение модели. Введем обозначения: h 0 = 0,7 м – высота столба воды в первом сосуде, h 1 и h 2 – понижение и повышение уровней ртути в сосудах, h 12 - расстояние между начальным уровнем ртути и границей раздела воды и ртути в

пе р в о м с о с у де,

– выс о т а с т о л ба в о ды над н а чал ь ным у р ов н е м. И з обр а зим

h 22

схематично происходящий процесс.

Используя условие равновесия жидкости в сообщающихся

2 - й э т ап . Разра б о т к а вы ч исли т е льно г о а л г о ри т м а .

сосудах, получим:  в gh 1   р gh 22 , где

•  в gh 2   р gh 12

(1).

У с л о в ие н е сжи м а ем о с т и , а т ак ж е доп о лн и т ельны е у с л ов и я задачи позволяют составить следующие уравнения:

Решим уравнения (1) – (4) совместно относительно

неизвестных h 22 и h 1 :

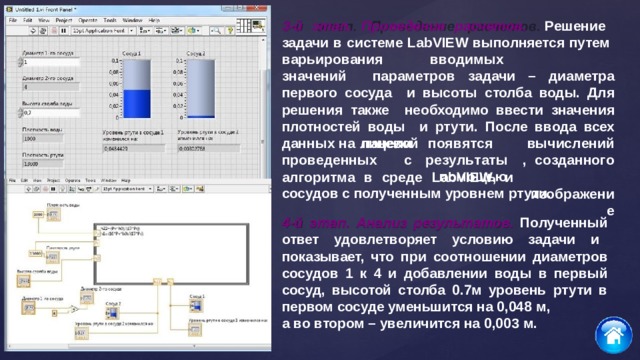
Рассмотрим процесс в среде LabVIEW. Создадим новый проект. Сформируем интерфейс пользователя. Для этого разместим на лицевой панели следующие элементы:

• два Numeric Control для задания диаметра 1-го сосуда и высоты столба воды;
• пять Numeric Indicator для вывода значений числовых величин;
• два элемента Tank для визуального отображения изменения уровня ртути.

Ф ормирование блочной диаграммы. На диаграмме расположены узлы, соответствующие элементам интерфейса. Вычислим величину диаметра второго сосуда с помощью арифметического узла Multiply и числовой константы. Для вывода результата умножения соединим выход узла Multiply с входом соответствующего Numeric Indicator.

Для решения задачи нужно расположить на диаграмме структуру Formula Node, позволяющую

вычислять значения неизвестных согласно значению входящих параметров. Введем в созданную

о б л а с т ь п о л у ч енны е ф о р м у л ы дл я вычи с л ения

и h 1 . Создадим на границе области три

h 22

терминала для ввода необходимых данных: плотности воды, плотности ртути и высота столба воды в первом сосуде. Добавим два терминала для вывода результатов вычислений.

Создадим числовую константу для ввода значения плотности воды. Подсоединим константу к входу числового индикатора, а также к терминалу Formula Node. Аналогичные действия проделаем для ввода значения плотности ртути. Подключим к терминалу области вычислений узел Numeric Control, соответствующий уровню воды в первом сосуде. Терминалы для вывода результатов соединим с узлами Tank и Numeric Indicator.

3-й этап. Проведение расчетов. Решение задачи в системе LabVIEW выполняется путем в а р ьиро в а ния в в о дим ы х зн а ч е н и й параметров задачи – диаметра первого сосуда и высоты столба воды. Для решения также необходимо ввести значения плотностей воды и ртути. После ввода всех данных на лицевой

вы ч ис л е н ий, с о зда н но г о и з обра ж е н ие

п а нели п о я в я т с я р е з у л ь т а т ы

п о м о щ ью

с

п р о в ед е н н ых

ал г ор и т м а в ср е де LabVI E W , и

сосудов с полученным уровнем ртути.

4-й этап. Анализ результатов. Полученный ответ удовлетворяет условию задачи и показывает, что при соотношении диаметров сосудов 1 к 4 и добавлении воды в первый сосуд, высотой столба 0.7м уровень ртути в первом сосуде уменьшится на 0,048 м,

а во втором – увеличится на 0,003 м.