Технология обучения решению расчётных задач по химии в 8 классе
Решение расчетных задач – важная сторона обучения химии. Обучение решению таких задач способствует связи обучения с жизнью, помогает профессиональной ориентации. Оно играет важную роль в воспитании трудолюбия, целеустремленности, формирования мировоззрения и реализации межпредметных связей. Велика развивающая функция задач по химии, т.к. в процессе их решения формируются рациональные приемы мышления, происходит обобщение знаний, устраняется формализм в знаниях, развивается самостоятельность и навыки самоконтроля.
Образовательная функция задач выражается в том, что в процессе их решения закрепляются и совершенствуются химические понятия о веществах и процессах.
Особенность любой химической задачи в том, что она всегда конкретна и всегда может быть решена на основе имеющихся знаний законов, теорий и фактов химии.
Процесс решения задачи – путь от абстрактного к конкретному. Однако всегда должны помнить, что задача – это не самоцель, а средство, способствующее прочному усвоению знаний, а значит к формированию интереса учащихся к изучению химии.
Для того чтобы обучить учеников способам решения расчетных задач, учителю самому необходимо в совершенстве овладеть химической задачей, способами ее решения, методикой ее использования. Умение решать расчетные задачи и обучать этому учеников – важная составляющая часть педагогического мастерства учителя химии.
В решении задач должен соблюдаться единый методический подход. Одна сторона этого подхода – обучение учащихся решению задач. Другая сторона – самостоятельное решение задач школьниками. И высшая степень проверки умения осмысленного решения задач – это составление условия задачи самими учащимися.
Выбирая задачу для учащихся необходимо оценить ее методически с точки зрения разных целей:
1.Какие понятия, законы, теории и факты должны быть закреплены в решении конкретной задачи;
2.Какие приемы решения задачи должны быть сформированы;
3.Какие мыслительные приемы должны быть развиты в процессе решения задачи;
4.Какие дидактические функции выполняет решение данной задачи: повторение, обобщение, закрепление нового материала или проверка знаний.
Работая с расчетными задачами, я использую логико-структурную схему, основные этапы которой:
1.Задача (функция учителя) →
2.Анализ условия задачи (функция учителя и ученика) →
3.План решения задачи (функция учителя и ученика) →
4.Реализация плана решения (функция учителя и ученика):
- химизм в содержании условия задачи;
- работа с условиями данной задачи;
- осмысление результата (вопроса) решения задачи;
- выбор способа ее решения;
- решение задачи;
- предложение других способов решения;
4.Анализ решения (функция учителя и ученика).
I Этап. Выбор задачи всегда остается за учителем. В настоящее время в распоряжении учителя имеется достаточное количество задач, соответствующих школьной программе.
II Этап. Анализ условия задачи предусматривает не только ознакомление с ее текстом, но и, что очень важно, правильную запись условия задачи с четким правильным использованием единых обозначений и определенной формы записи.
Даже, если задача решается по уравнению химической реакции, очень важно записать сначала ее условие.
III – IV Этапы. Мы с учащимися используем тот или иной математический подход к решению каждой химической задачи.
V Этап. Анализ решения задачи, пожалуй, так же важен, как и само решение. Особенно при обучении решения задач нового типа, т. к. анализ позволяет выявить недостатки решения, найти его наиболее рациональный способ, установить и закрепить в памяти приемы, использованные при решении.
При первоначальном знакомстве школьников с решением типовой задачи необходимо разъяснить ее условие, добиться понимания учениками новых терминов и понятий, которые им придется использовать при решении задач.
Для лучшего понимания условия задачи обязательно провожу 2-х минутный химический тренажер. Пожалуй, его можно здесь назвать как «устный счет».
При изучении темы «Расчеты по химическим формулам», мы с ребятами сами выводим формулу, по которой проведен химический тренажер.
Например: им знакомо понятие относительная молекулярная масса, молярная масса. Находим устно молярную массу воды: М(Н2О) = 18 г/моль – это масса одного моля. Провожу устный счет:
- чему равна масса 2; 3; 4; 10; 0,5; 0,1 и т. д. молей?
Ребята отвечают, и в конце тренажера мы выводим формулу нахождения массы вещества: m = ν · М.
Подобные тренинги помогают вывести и остальные формулы, которые мы впоследствии будем использовать на каждом уроке темы «Количественные отношения в химии»: N = ν · Nа, V = ν · Vm, ν = 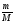 , ν =
, ν = 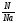 , ν =
, ν = 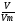 .
.
А чтоб ребята не забывали их, впоследствии на уроках во время химической интеллектуальной разминки можно включать этот устный счет по химическим формулам.
После химического тренажера и вывода формулы обращаю внимание ребят на форму записи условия задачи и хода ее решения, а также на формулировку ответа.
На уроках стараюсь давать задачи систематически: при освоении нового материала, при закреплении и в процессе проверки знаний учебного материала. Если ученик научатся хорошо решать задачи, то каждая решенная ими задача станет для ребят маленькой личной победой. Пусть задачи поначалу будут простейшими. Научившись хорошо решать несложные задачи, ребята обязательно захотят покорить следующую высоту – более сложную. Нам важно поддерживать в них это желание, вовремя направить и оказать помощь. В восьмом классе дифференциации при решении задач быть не может – каждый должен научиться решать простейшие задачи. В дальнейшем, конечно, дифференциация возможна даже в условии, формулировке задачи, а не только в выборе задач разной степени сложности. Для слабых ребят – работа с алгоритмом. Пусть используют его, пока не научатся.
Методика решения задач прямого расчетного действия
Методика решения задач этого типа предполагает два способа решения: метод пропорций и алгебраический метод. Метод пропорций желательно применять лишь при решении несложных задач программы. Но если мы хотим научить ребят решать задачи любой степени сложности, необходимо применение алгебраического метода, позволяющего использовать известные нам уравнения связи:
| m = ν · М | ν = 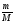 | ν = 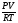 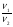 = = 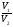
| ωр.в =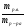 ω(Э) = 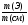 |
|
| N = ν · Na | ν = 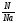 | φгаза = 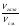 |
| V = ν · Vm | ν = 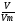 |
|
Решать задачи с использованием этих формул с использованием этих формул можно двумя способами: от условия задачи и от вопроса, поставленного в ней.
Задача 1. Определите объем, занимаемый при н. у. углекислым газом, масса которого равна 22г.
| Дано: m(СО2) = 22г |
| V( СО2) = ? |
Решение:
1. Начинаем решать от вопроса, поставленного в задаче – записываем ведущую формулу нахождения объема газа:
V(СО2) = ν(СО2) ·Vm
2. Видим, что количество газа ν(СО2) нам неизвестно. Находим его, используя одно из уравнений связи, подходящее под условие задачи:
ν(СО2) = 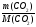 , М(СО2) = 44г/моль;
, М(СО2) = 44г/моль;
ν(СО2) = 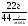 = 0,5моля.
= 0,5моля.
3. Подставляем значение ν(СО2) в (1) уравнение связи и находим объем углекислого газа:
V(СО2) = 0,5моль · 22,4л/моль = 11,2л.
Ответ: V(СО2) = 11,2л.
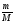 , ν =
, ν = 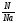 , ν =
, ν = 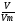 .
.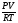
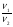
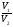
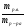
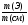
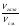
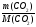 , М(СО2) = 44г/моль;
, М(СО2) = 44г/моль;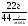 = 0,5моля.
= 0,5моля.















