( 1 слайд).
В лабораторной практике и при решении олимпиадных задач приходится встречаться со случаями приготовления растворов с определенной массовой долей растворенного вещества, смешением двух растворов разной концентрации или разбавлением крепкого раствора водой. В некоторых случаях можно провести достаточно сложный арифметический расчет. Однако это малопродуктивно. Чаще для этого лучше применить правило смешения (диагональную модель «конверта Пирсона», или, что то же самое, правило креста). Но данный способ решения задач исключен из школьной программы по химии.
(2 слайд)
Актуальность исследования обусловлена тем, что при подготовке к олимпиадам, и успешной сдачи ГИА, ЕГЭ школьникам необходимы знания, которые выходят за рамки школьной программы.
(3 слайд)
Цель работы: научиться решать задачи методом «Конверта Пирсона».
(4 слайд)
Задачи:
- найти методику решения задач методом «Конверта Пирсона»;
- выбрать задачи.
- практически применить знания по решению таких задач.
(5 слайд)
Методы исследования:
- Поиск информации
- Анализ задач
(6 слайд).
Немного о Пирсоне.
Карл Пирсон родился 27 марта 1857года в Лондоне, умер 27 апреля 1936, там же.
английский математик, статистик, биолог и
философ; основатель математической статистики,
один из основоположников биометрики.
Автор свыше 650 опубликованных научных работ.
(7 слайд)
Рассмотрим методику решения задач «Конверт Пирсона»
Допустим, нужно приготовить раствор определенной концентрацией, имея в расположении два раствора с более высокой и менее высокой концентрацией, чем нужно нам. Тогда, если обозначить массу первого раствора через m1, а второго – через m2, то при смешивании общая масса смеси будет слагаться из суммы этих масс. Пусть массовая доля растворенного вещества в первом растворе – ω1, во втором – ω2, а в их смеси – ω3. Тогда общая масса растворенного вещества в смеси будет слагаться из масс растворенного вещества в исходных растворах:
m 1ω1 + m2ω2 = ω3(m1 + m2).
Отсюда
m1(ω1 – ω3)= m2(ω3 – ω2).
Видно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворенного вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.
(8 слайд)
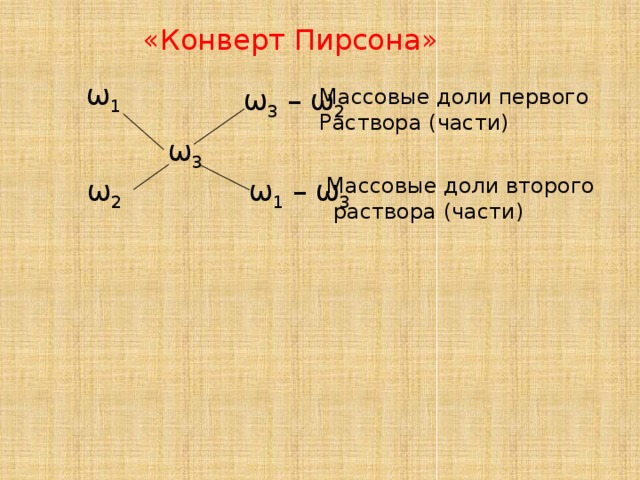
При расчетах записывают одну над другой массовые доли растворенного вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение. Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.
ω1 ω3 – ω2
массовые доли первого
ω3 и второго растворов
ω2 ω1 – ω3
(9 слайд)
Для пояснения этого правила решим следующие задачи:
1.К 15 г 10% раствора соли добавили5% раствор
соли и получили 8% раствор. Какое количество
граммов 5%-го раствора добавили?
Для начала решим эту задачу обычным арифметически способом и сравним со способом решения по правилу креста.
(10 слайд)
Возьмем за х массу 5% раствора,
10% раствор весит 15г, тогда 8% раствор весит 15+х
Переведем массовые доли в части:
5% - 0,05; 10% - 0,1; 8% - 0,08
Составим уравнение:
0,05х + 15• 0,1 = (15 + х) • 0,08
0,05х + 1,5 = 1,2+ 0,08х
0,05х-0,08х = 1,2-1,5
-0,03х=-0,3
Х=10
Ответ: необходимо добавить 10г 5% раствора, чтобы получить 8% раствор
(11 слайд)
А теперь решим данную задачу правилом креста.
Запишем массовые доли исходных растворов друг под другом, а справа между ними массовую долю полученного раствора. По диагонали вычтем из большего числа меньшее, получаем число частей необходимых для приготовления раствора.
По первому раствору найдем массу одной части: 15г / 3 = 5г – масса 1 части
Теперь умножим массу одной части на 2 части 5% раствора и получим массу этого раствора: 2 ? 5г = 10г
Ответ: необходимо добавить 10г 5% раствора,
чтобы получить 8% раствор.