Разработка по учебнику Смирнов В.А., Туяков Е.А. Геометрия 10. Учебник для 10 классов общественно-гуманитарного направления общеобразовательных школ для I курса колледжа. Цель: знать понятие угла между прямой и плоскостью, а также уметь находить углы между прямой и плоскостью; знать теорему о трех перпендикулярах и уметь применять ее при решении задач
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Угол между прямой и плоскостью. Теорема о трёх перпендикулярах»
Полезное для учителя
Распродажа видеоуроков!
1840 руб.
3060 руб.
1750 руб.
2920 руб.
1660 руб.
2770 руб.
1720 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
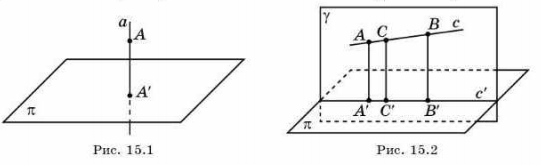
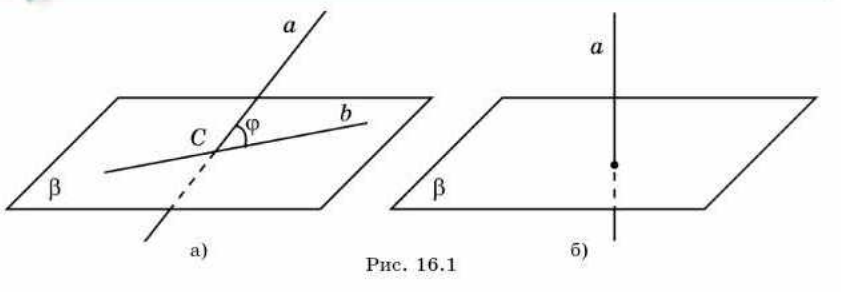
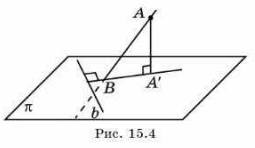 еорема (о трех перпендикулярах). Если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной.
еорема (о трех перпендикулярах). Если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной.