| Этап урока | Деятельность учителя | Деятельность ученика | Формируемые УУД |
| 1этап. Организационный этап (1 мин)
| Приветствует учащихся, проверяет их готовность к уроку. Настраивает учащихся на урок. Эпиграф "Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью" Л.Н.Толстого ( слайд 2)
| Учащиеся слушают учителя, включаются в деловой ритм урока.
| Личностные: Уважение личности и её достоинства, доброжелательное отношение к окружающим. Регулятивные: Формирование способности к организации своей деятельности.
|
|
2 этап. Актуализация знаний и фиксация индивидуальных затруднений в деятельности (3 мин)
| Предлагает учащимся в парах найти ошибки в решении задачи.
Раздаёт карточки. Найди «ошибку» в заданиях 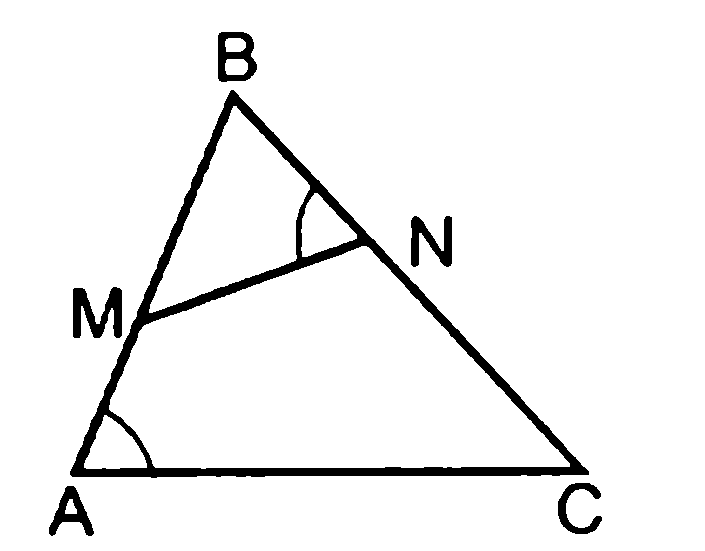
1)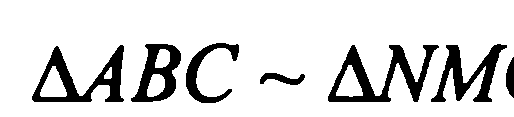 B по двум углам , т.к. угол А= углу BMN как соответственные углы при параллельных прямых MN и АС и секущей АВ и угол В –общий. B по двум углам , т.к. угол А= углу BMN как соответственные углы при параллельных прямых MN и АС и секущей АВ и угол В –общий.
2)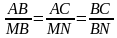
3) ; AC=18см ; AC=18см
| Слушают инструкцию по решению задания. Выполняют задания. Обсуждают и находят ошибки. Пары, которые нашли ошибки, сообщают о выполнении. Аргументируют своё решение учителю.
В 1) угол А не может равняться углу BMN как соответственные углы, т. к. прямые MN и АС не параллельные. Правильный ответ 1.угол В –общий. 2.угол А =углу BNM по условию. В 2 ) неверно записана пропорциональность сторон 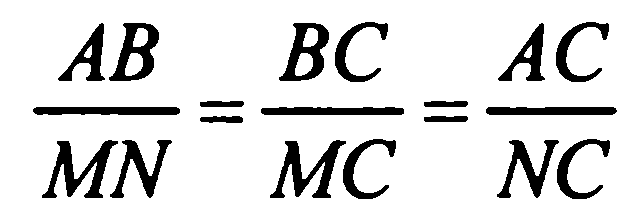 В 3) вычислительная ошибка. Неверно применено свойство пропорции 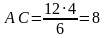 см. см.
| Личностные: Умение контролировать процесс и результат учебной математической деятельности. Регулятивные: Осуществляют самоконтроль и взаимоконтроль, проверяя ответ на соответствие условию; вносят необходимые дополнения и коррективы в план и способ действия; вносят изменения в результат своей деятельности, деятельности товарища.
Коммуникативные: Представляют конкретное содержание и сообщают его в письменной форме; адекватно аргументируют свою точку зрения, стараются прийти к общему мнению.
Познавательные: решают задачи на подобие, решают пропорцию. |
| 3 этап. Выявление причины затруднений и постановка цели деятельности (7 мин)
| Предлагает рассмотреть картинку На рисунке изображение двускатной крыши. (слайд 3) Эвристическая беседа. Какие геометрические фигуры изображены на картинке? Какие треугольники? 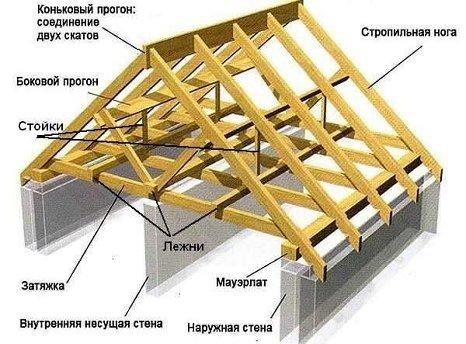
После учитель предлагает проекцию крыши ( слайды 4-5) 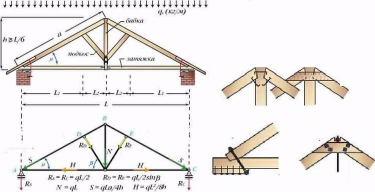
и подводит учащихся к созданию проблемной ситуации. Задача найти длину лежень СD,если ВD=4,а АD =1.
Сможем ли мы найти искомую величину? Предлагает вернуться к задаче чуть позже Ведет диалог с учащимися: 1.Чем является СD в треугольнике АВС? 2. Что сделала высота с треугольником АВС? 3.Сколько треугольников всего? 4. Что объединяет эти треугольники? 5.Что можно найти из подобия треугольников?
Показывает тему на слайде 6.
6.Попробуйте доказать подобие треугольников АСВ и АСD.
Выделите два отношения. Которые связывают одинаковые величины.
Почему эти отношения?
Чем является АС в треугольнике АВС? АВ ? АD? Попробуйте сформулировать правило.
Сможем ли мы ответить на вопрос задачи? Предлагает рассмотреть другие пары треугольников | Учащиеся рассматривают чертёж и в ходе беседы отвечают на вопросы учителя
Прямоугольники, треугольники.
Равнобедренные и прямоугольные.
При решении задания, учащиеся осознают, что возникла проблемная ситуация, обсуждают ее с учителем (решить задачу не получилось, не хватает данных).
Отвечают на поставленные вопросы Участвуют в диалоге.
1. СD высота
2.разбила на прямоугольные треугольники АВD и СDB 3.3 треугольника 4. Они подобны между собой 5. Пропорциональные отрезки в треугольниках Формулируют тему и цели урока. Записывают тему урока : « Пропорциональные отрезки в прямоугольном треугольнике» в тетрадях. Задачи: Найти новые правила для пропорциональных отрезков в прямоугольном треугольнике. Сформулировать правила; научиться применять правила при решении задач.
6.Учащийся у доски доказывает подобие треугольников, остальные записывают в тетради. (Треугольники подобны по первому признаку, т.к.у них есть по два равных угла 1.) угол АСВ равен углу АDC и 2)угол А общий ). Углы равны, а стороны пропорциональны 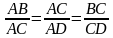
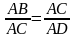
Дважды встречается АС . Можно найти 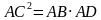 . . 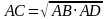 . . АС -катет АВ -гипотенуза АD- Отрезок гипотенузы Катет прямоугольного треугольника равен корню квадратному из произведения гипотенузы и отрезка гипотенузы, заключенному между катетом и высотой, проведенной из вершины прямого угла
Нет.
Подобие треугольников АВС и ВСD приведёт к аналогичному результату. Самостоятельно доказывают подобие треугольников АВС и ВСD. ( подобны по первому признаку 1.) угол В общий
2) угол АСВ равен углу СDВ. Делают выводы : . . 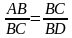 . .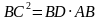 . . 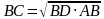
Проверяют в парах правильность доказательства через презентацию.
| Личностные: Ответственное отношение к учению; готовность и способность учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; умение ясно, точно, грамотно излагать свои мысли в устной речи, понимать смысл поставленной задачи, выстраивать аргументацию.
Коммуникативные:Адекватно используют речевые средства и аргументируют свою позицию; представляют конкретное содержание и сообщают его в письменной и устной форме.
Познавательные: Анализируют и осмысливают текст задачи. |
| 4 этап. Построение проекта выхода из затруднения (6 мин)
| Чтобы найти выход из проблемной ситуации, предлагает учащимся решить ещё одну задачу: доказать подобие треугольников третьей пары АDC и ВСD. Доказывает вместе с учащимися
Предлагает сформулировать правило. | Оформляют решение в тетрадях и на доске.
У треугольников 1) угол ADC равен углу BDC.2) Угол ACD=  и и если из ,то это будет угол В. Поэтому угол ACD=углу B.Так как треугольники подобны по двум углам,то ,то это будет угол В. Поэтому угол ACD=углу B.Так как треугольники подобны по двум углам,то  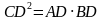

Через вывод треугольников получают второе правило. Формулируют правило :высота прямоугольного треугольника, проведенная из вершины прямого угла равна корню квадратному из отрезков гипотенузы, на которые делится гипотенуза этой высотой.
| Личностные: Готовность и способность учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию; умение контролировать процесс и результат учебной математической деятельности; готовность к осуществлению исследовательской деятельности. Регулятивные:Критически оценивают полученный ответ; осуществляют самоконтроль, проверяя ответ на соответствие условию; вносят изменения в результат своей деятельности, исходя из оценки этого результата самим обучающимся, учителем, товарищами. Коммуникативные:Адекватно используют речевые средства и аргументируют свою позицию; учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, договариваются о совместной деятельности, приходят к общему решению. Познавательные:Анализируют и осмысливают решение задач; извлекают необходимую информацию, моделируют условие с помощью рисунков; строят логическую цепочку рассуждений, работая в «зоне ближайшего развития»; проводят несложные исследования, связанные с отношениями катетов и гипотенуз в прямоугольных треугольниках . |
| 5 этап. Реализация построенного проекта. Составление алгоритма. (5 мин) | Подводит учащихся к новому понятию среднего геометрического ( среднего пропорционального ). Проговаривает правило :ХУ называется средним пропорциональным или средним геометрическим для отрезков АВ и СD 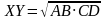 . . Предлагает сформулировать правила с помощью нового понятия и сверить с эталоном в учебнике на стр 146 , пункт 65.
Предлагает вернуться к нерешенной. задачи. Сможем ли мы найти сейчас длину лежни?
|
Формулируют полученные правила для катетов и высоты с помощью понятия среднего геометрического. 1.Правило: Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла. 2.Правило: Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков гипотенузы, на которые делится гипотенуза этой высотой. Открывают учебники п 65, стр 146 Еще раз про себя внимательно читают правила. Проговаривают формулировки хором за учителем и в парах. Да. Учащиеся находят искомую величину. СD=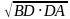 = =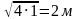 | Личностные: Готовность и способность учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; умение контролировать процесс и результат учебной математической деятельности; Регулятивные:Критически оценивают полученный ответ; осуществляют самоконтроль, проверяя ответ на соответствие условию. Коммуникативные:Адекватно используют речевые средства и аргументируют свою позицию; представляют конкретное содержание и сообщают его в письменной и устной форме; учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, договариваются о совместной деятельности, приходят к общему решению. Познавательные: Формулируют, записывают с помощью букв правила действий с обыкновенными дробями. |
| Физкультминутка (1 мин) | Предлагает отдохнуть. Дружно с парты вместе встали. Руки вверх, потом назад, Шаг вперёд, потом назад, Вправо, влево повернись И за парту снова садись. | Меняют вид деятельности (отдохнули), готовы к продолжению работы. |
|
| 6 этап. Первичное закрепление во внешней речи учащихся. (6 мин) | Предлагает записать формулы с новыми обозначениями по чертежу ( слайд 7)
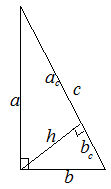 по чертежу. по чертежу.
из учебника для закрепления алгоритма.№ 572 (а). | Записывают формулы в тетради с проговариванием правил на доске. 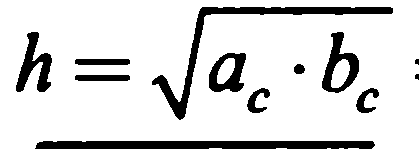 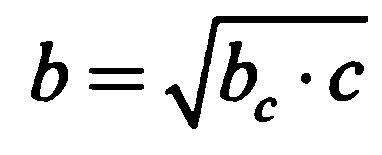

Открывают учебники на стр.152, № 572 (а) Учащийся решает задачу, записывает решение на доске, комментируя записи. Дано: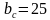 , , 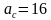 Найти 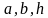 Решение: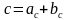 c=25+16=41 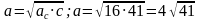
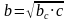 ; ;
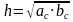 ; ;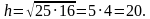
| Личностные: Умение контролировать процесс и результат учебной математической деятельности; Регулятивные:Критически оценивают полученный ответ; осуществляют самоконтроль, проверяя ответ на соответствие условию. Коммуникативные:Адекватно используют речевые средства и аргументируют свою позицию. Познавательные: Выполняют действия с пропорциональными отрезками. |
| 7 этап. Самостоятельная работа с самопроверкой по эталону. (5 мин) | Предлагает выполнить самостоятельно задание и проверить в парах. Слайд 8. В презентации – эталон записи и ответы. Дано: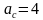 ,с=9 ,с=9 Найти: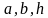 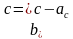
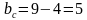
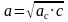
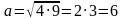 ; ;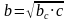
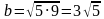
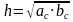

| Выполняют задание в тетради самостоятельно. Сверяются с эталоном, корректируют решение. Оценивают друг друга.
| Личностные: Умение контролировать процесс и результат учебной математической деятельности; Регулятивные: Осуществляют взаимоконтроль, проверяя ответы на соответствие условию; вносят необходимые дополнения и коррективы в план и способ действия в случае расхождения реального действия и его результата; вносят изменения в результат своей деятельности, исходя из оценки этого результата. Познавательные: Выполняют действия с пропорциональными отрезками. |
| 8 этап. Включение в систему знаний и повторение (3 мин) | Подводит к завершению урок. Какие величины можно найти с помощью правил? Подводит итог вместе с учащимися.
| Обсуждают. Отвечают Можно найти высоту, катет, гипотенузу, отрезки гипотенузы Обосновывают выбор. Замотивированы на следующий урок.
Подводят итог урока: озвучивают тему, проговаривают, удалось ли им реализовать поставленные задачи. | Личностные: Анализ и сравнение с целью выделения признаков; подведение под понятие и алгоритм. Регулятивные: Осуществляют самоконтроль, фиксируют в обобщенном виде новый способ действий в речи и знаково;
Коммуникативные:Адекватно используют речевые средства и аргументируют свою позицию. |
| 9 этап. Рефлексия учебной деятельности на уроке (2 мин) | Проводит рефлексию результатов и деятельности. Задаёт вопросы Всё ли я понял(а)на уроке, если да, то погладить себя по голове.( я молодец) Я научился применять формулы для решения задач. Если да, то погладить себя по голове( я молодец) У меня хорошее настроение, если да, то погладить себя по голове( я молодец)
| Принимают участие в рефлексии. Отвечают на вопросы учителя.
если да, то погладить себя по голове.( я молодец) если да, то погладить себя по голове( я молодец)
если да, то погладить себя по голове( я молодец)
| Личностные: Умение контролировать процесс и результат учебной математической деятельности; Регулятивные:Критически оценивают полученный результат. |
| 10 этап. Домашнее задание, инструктаж (1 мин) | Проговаривает и комментирует домашнее задание.
Благодарит за урок. Слайд 9. | Слушают, записывают задание в дневник. п 65 , № 572(б,г,д),574.
Встают. |
|

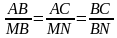
 ; AC=18см
; AC=18см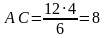 см.
см.

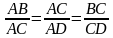
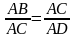
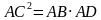 .
.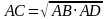 .
.  .
.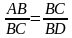 .
.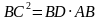 .
. 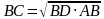
 и
и 
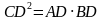

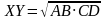 .
. 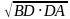 =
=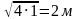
 по чертежу.
по чертежу.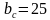 ,
, 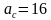
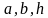
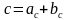
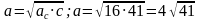
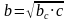 ;
;
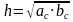 ;
;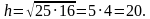
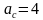 ,с=9
,с=9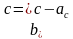
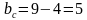
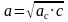
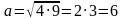 ;
;