| Посмотрите на экран. - Что вы видите? - Как вы думаете, что мы будем делать на уроке? 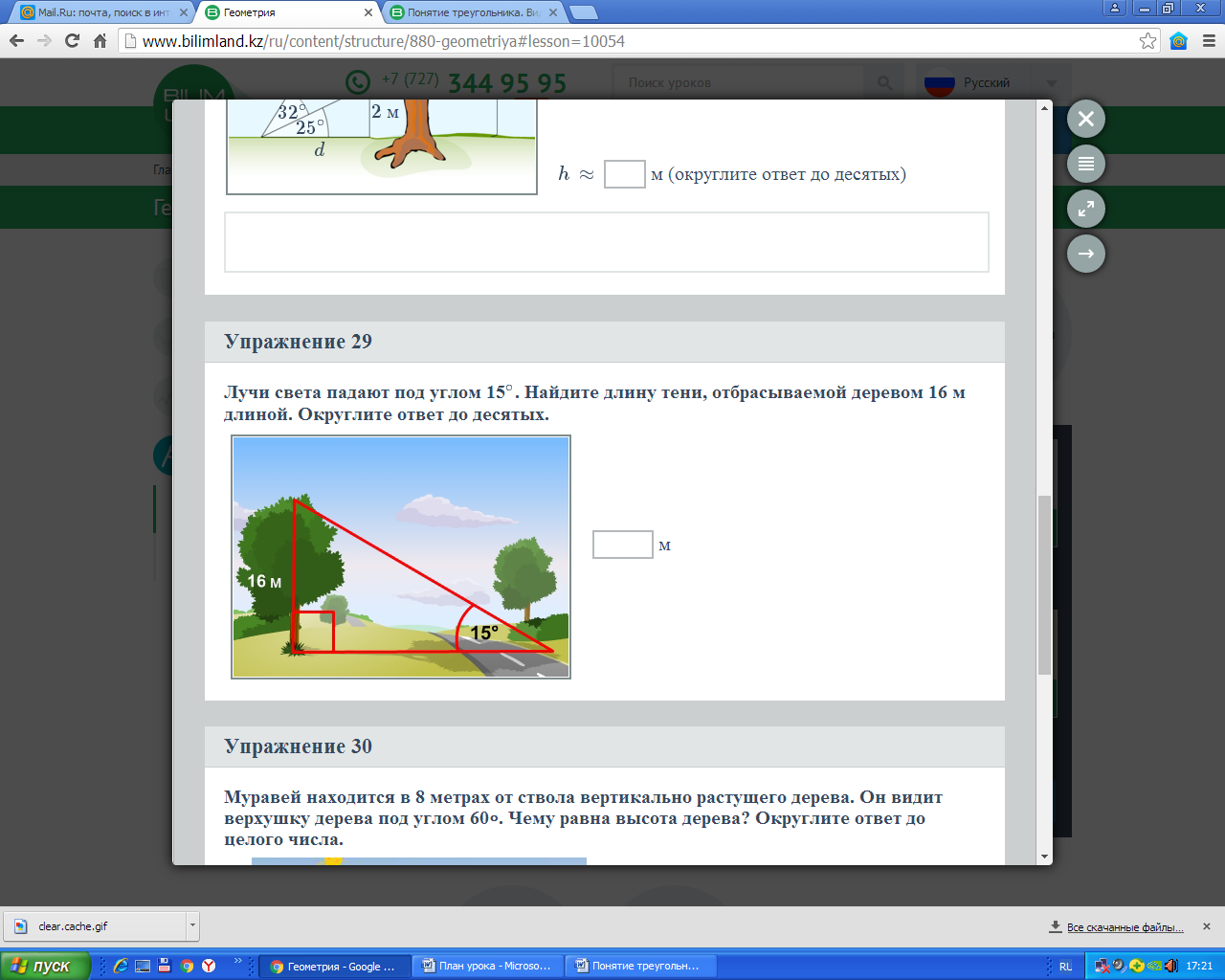
Тема нашего урока «Решение прямоугольных треугольников». - Запишите число и тему урока. - Какие цели нам необходимо поставить перед собой? Актуализация знаний ГР. Задание 1. Прием «Найди соответствие» в прямоугольном треугольнике | 1.Квадрат гипотенузы равен сумме квадратов катетов | А.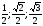 | | 2.отношение прилежащего катета к гипотенузе | Б..Тангенс острого угла | | 3.Сумма острых углов в прямоугольном треугольнике равна | В..Синус острого угла | | 4.отношение противолежащего катета к гипотенузе | Г.Котангенс острого угла | | 5.отношение прилежащего катета к противолежащему катету | Д.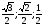 | | 6.отношение противолежащего катета к прилежащему. | Е.90◦ | | 7.значения синуса 30◦,45◦,60◦ равны | Ё.теорема Пифагора | | 8.значения косинуса 30◦,45◦,60◦ равны | Ж.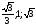 | | 9.Значения тангенса 30◦,45◦,60◦ равны | З.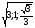 | | 10.значения котангенса 30◦,45◦,60◦ равны | Й Косинус острого угла | Каждая группа на доске вывешивают свои ответы. ФО: самопроверка по готовому ключу: 1Е,2Й;3Е;4В;5Г;6Б;7А;8Д;9Ж;10З. Учитель зачитывает правильные ответы. Обратная связь от учащихся. |
Учашиеся определяют тему урока и цель урока
Каждая группа получает карточку с заданием, выполнив его, на доске вывешивают свои ответы.
|
Учитель корректирует при необходимости
ФО: самопроверка по готовому ключу: 1Е,2Й;3Е;4В;5Г;6Б;7А;8Д;9Ж;10З.
| (Дифференциация по ресурсу)
Диалог и поддержка |
| Негізгі бөлім Основная часть
15 мин
10 мин
1 мин
5 мин | Изучение нового материала. Вопросы: Что значит «решить прямоугольный треугольник» ? Под решением прямоугольного треугольника понимают процесс нахождения неизвестных элементов по двум его заданным. Возникает вопрос Приём «Проблемный вопрос» - Сможем ли найти неизвестные элементы, если задать величины острых углов?
ГР. Задание 1. Составить алгоритм решения задачи на нахождение сторон и углов прямоугольного треугольника по двум заданным элементам. Сначала ученики работают в паре по стратегии «Подумай, обсуди, в паре поделись». Затем разбирают задание в группе. В каждой группе обсуждают выполнение своего задания. Учитель оказывает поддержку каждой группе, направляет их работу и оценивает их работу через устные комментарии. Далее по стратегии «Джигсо» учащиеся перераспределяются таким образом, чтобы в каждой новой группе оказались представители всех первоначальных групп. Применение данной стратегии направлено на взаимообучение, взаимоподдержку, способствует развитию ответственности за собственное обучение 1 группа. Даны катеты а и в, требуется найти гипотенузу с, острые углы 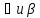 . . 2 группа. Даны гипотенуза с, катет а. Найти неизвестные элементы в, 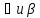 . . 3 группа. Даны катет а и острый угол  . Найти неизвестные элементы с, в, . Найти неизвестные элементы с, в, 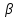 . . 4 группа. Даны гипотенуза с и острый угол  . Найти а, в, . Найти а, в, 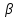 .. ..
Составленные в группах алгоритмы решения прямоугольных треугольников, т.е. нахождения сторон и углов прямоугольного треугольника по двум заданным элементам, вывешиваются на магнитной доске для последующего применения.
Закрепление изученного материала: Используя алгоритмы, в группах решают задачи. ГР. Задание 3. Уровень А. № 1 Даны катет a и противолежащий острый угол α прямоугольного треугольника. Найдите другие стороны и углы треугольника 1)а=5см :α=30° № 2 Даны катет a и прилежащий острый угол β прямоугольного треугольника. Найдите другие стороны и углы треугольника 1)а=6см; β=30°
№ 3 Даны катеты a и в прямоугольного треугольника. Найдите гипотенузу и углы треугольника 1)а=12см; в=5см
№ 4 Даны гипотенуза с и острый угол α прямоугольного треугольника. Найдите катеты и углы треугольника 1)с=16см; α=30°
| Критерии | Дескрипторы | | решает типичные задачи, используя алгоритм «решения прямоугольного треугольника» по двум заданным элементам; | - вычисляет гипотенузу по т.Пифагора; - катеты по т.Пифагора или через тригонометрические функции; - находит значение тригонометрических функций через отношения сторон; - находит величину угла по таблицам; - находит значение второго угла, используя свойство острых углов в прямоугольном треугольнике. |
Уровень В. Радиус окружности, описанной около прямоугольного треугольника с острым углом 30º равен 8см. Найдите катеты этого треугольника. равен 8см. Найдите катеты этого треугольника.
Уровень С. Медианы, проведённые к катетам прямоугольного треугольника относятся как 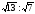 . Найдите углы треугольника . Найдите углы треугольника
| Критерии | Дескрипторы | | решает задачи на нахождение медиан и высот прямоугольного треугольника.
| Уровень В -находит гипотенузу по формуле с=2R; -находит катет по свойству угла 30; -находит второй катет используя в=с cos30. Уровень С -выражает катеты через а и в; -выражает медианы через катеты и составляет пропорции; -находит отношение катетов; -находит тангенс острого угла -находит величину острого угла -находит величину второго острого угла. |
Учитель раздает дескрипторы для самооценки. Комментируя работу учащихся, учитель строит подмостки для тех учащихся, которые решили задачу уровня С.
Физминутка: Потрудились - отдохнем Встанем, глубоко вздохнем Руки в стороны, вперёд Влево, вправо, поворот Три наклона, прямо встать Руки вниз и вверх поднять Руки плавно опустили Всем улыбки подарили. Для определения применения знаний по теме на практике провожу мини исследовательскую работу.
Практическая работа Из каждой из четырех групп выбираю по одному сильному ученику, предлагаю создать пары. За отдельными столами перед классом, предлагается выполнить практическую работу, те учащиеся, которые в группе тоже по инструкции, полученной от учителя, анализируют и пытаются найти решение. Их главная роль, дать объективную оценку деятельности учеников, выполняющих практическую работу по стратегии две звезды и одно пожелание. Инструкция для учащихся. Группа №1. Задание №1.(практическая работа) С помощью веревки и линейки вычислите: Как правильно сидя за столом читать книгу. Учитывая оптимальное расстояние учебника от глаз 50см. 1) Найдите расстояние от тела до книги. 2) Определите под каким углом нужно читать книгу. Работу поделите по ролям. Учтите длину книги. Обсудите в группе. Запишите в постере. Объясните такое расположение. ФО. Наблюдение. (Отмечаю каждого на листе оценивания по работе в группе). Презентация у доски с помощью интерактивной доски и постера. Дескрипторы: 1. Строит чертеж. 2. Измеряет высоту от глаз до парты. 3. Использует теорему Пифагора. 4. Находит длину основания. 5. Через синус или косинус находит искомый угол. (Принимаю альтернативное решение задачи). Группа №2. Задание №1.(практическая работа) С помощью рулетки и линейки вычислите: Определите, как поставить елку по центру комнаты. Как можно вычислить центр с помощью диагонали основания комнаты? Работу поделите по ролям. Запишите в постере. Объясните работу. ФО. Наблюдение. (Отмечаю каждого на листе оценивания по работе в группе). Презентация у доски с помощью интерактивной доски и постера. Дескрипторы: 1. Строит чертеж. 2. Измеряет длину комнаты.. 3. Измеряет ширину комнаты. 4.Использует теорему Пифагора. 5.Находит диагональ. 6.Находит середину диагонали. (Принимаю альтернативное решение задачи).
|
Ученик уровня С делает вывод: С помощью двух острых углов мы не сможем однозначно определить прямоугольный треугольник, т.к. эти два элементы являются зависимыми посредством равенства α+β=90
В каждой группе обсуждают выполнение своего задания. Далее по стратегии «Джигсо» учащиеся перераспределяются таким образом, чтобы в каждой новой группе оказались представители всех первоначальных групп
Составленные в группах алгоритмы решения прямоугольных треугольников, т.е. нахождения сторон и углов прямоугольного треугольника по двум заданным элементам, вывешиваются на магнитной доске для последующего применения
Все учащиеся решают задачи уровня А, большинство решают задачу уровня В, некоторые решают задачу уровня С
Две пары учащихся выполняют практическую работу перед группами, остальные, изучив инструкцию, наблюдают за проведением работы и объективно оценивают ее по стратегии Две звезды, одно пожелание
|
Комментарии учителя.
Самооценивание по дескрипторам. Комментарии учителя
Комментарии учителя. Оценивание детей по стратегии Две звезды, одно пожелание.
|
Поэтапная коррекция ответов учащимися, оказание поддержки учителем с учетом потребности группы
Дифференциация по уровню задания. На данном этапе урока учащимся раздаются задания трех уровней А,В,С решение которых направлены на реализацию целей по таксономии Блума
Диф-я по темпу Диалог и поддержка при необходимости
|

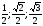
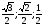
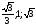
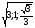
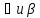 .
. . Найти неизвестные элементы с, в,
. Найти неизвестные элементы с, в, 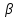 .
. равен 8см. Найдите катеты этого треугольника.
равен 8см. Найдите катеты этого треугольника.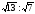 . Найдите углы треугольника
. Найдите углы треугольника















