Механика наряду с задачами движения материальной токи включает задачи динамики системы материальных точек, к которым, прежде всего, относится задачи с поступательным движением связанных друг с другом тел. Например: электровоз тянет состав вагонов, вертолет поднимает на тросе грузы. Эти задачи можно свести к задаче динамики отдельной материальной точки. Только в этом случае следует «мысленно» разделить ее в тех местах, где условно требуется определить силы.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Алгоритм решения задач повышенной трудности на движение связанных тел
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Алгоритм решения задач повышенной трудности на движение связанных тел»
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1670 руб.
2780 руб.
1610 руб.
2690 руб.
1520 руб.
2530 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства


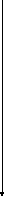
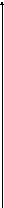
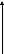 Схематический чертеж:
Схематический чертеж: Y N1
Y N1
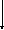

 a
a

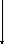
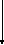

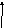
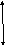

 а N T T
а N T T
 m2g
m2g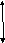

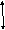


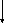
 Y m1g
Y m1g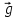 , со стороны нити – сила натяжения нити
, со стороны нити – сила натяжения нити 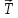 . По условию задачи под действием приложенных сил эта гирька поднимается вверх с ускорением а, поэтому Тm1g.
. По условию задачи под действием приложенных сил эта гирька поднимается вверх с ускорением а, поэтому Тm1g. 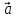 ОУ
ОУ















