Математика,
если на нее правильно посмотреть,
отражает не только истину,
но и несравненную красоту.
Бертран Рассел.
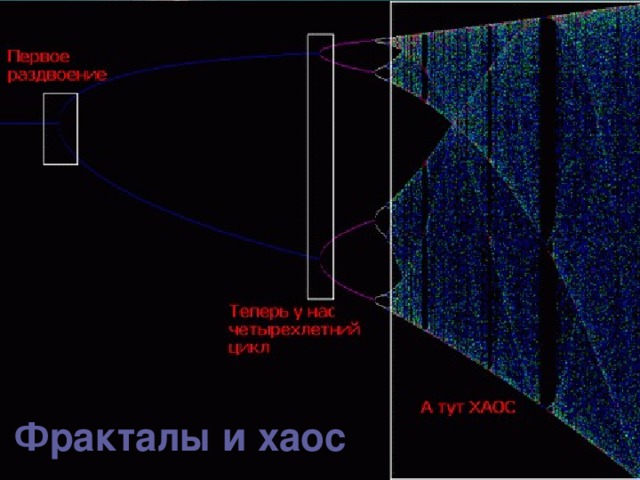
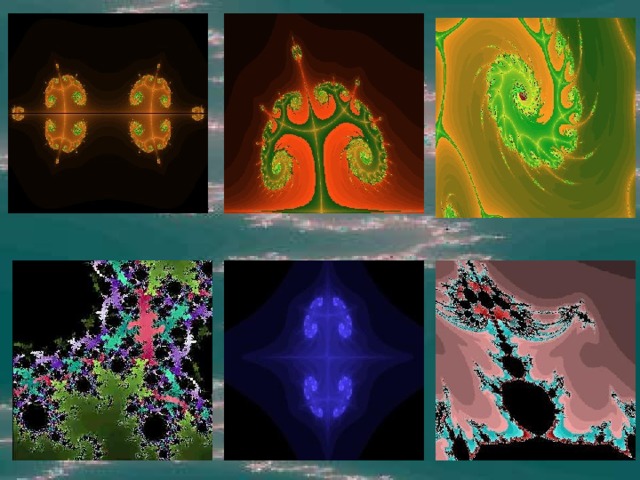
Вы, конечно же, слышали о фракталах. Вы, конечно же, видели эти захватывающие картинки более реальные, чем сама реальность. Горы, облака, кора дерева - все это выходит за рамки привычной евклидовой геометрии. Мы не можем описать камень или границы острова с помощью прямых, кружков и треугольников. И здесь нам приходят на помощь фракталы. Что же это за знакомые незнакомцы? Когда они появились?
История появления.
Первые идеи фрактальной геометрии возникли в 19 веке. Кантор с помощью простой рекурсивной (повторяющейся) процедуры превратил линию в набор несвязанных точек (так называемая Пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками. Пеано нарисовал особый вид линии (рисунок №1). Для ее рисования Пеано использовал следующий алгоритм.
На первом шаге он брал прямую линию и заменял ее на 9 отрезков длиной в 3 раза меньшей, чем длина исходной линии (Часть 1 и 2 рисунка 1). Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость. Доказано, что для каждой точки на плоскости можно найти точку, принадлежащую линии Пеано. Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических объектов. Они не имели четкой размерности. Пыль Кантора строилась вроде бы на основании одномерной прямой, но состояла из точек (размерность 0). А кривая Пеано строилась на основании одномерной линии, а в результате получалась плоскость. Во многих других областях науки появлялись задачи, решение которых приводило к странным результатам, на подобие описанных выше (Броуновское движение, цены на акции).
Отец фракталов
Вплоть до 20 века шло накопление данных о таких странных объектах, без какой либо попытки их систематизировать. Так было, пока за них не взялся Бенуа Мандельброт - отец современной фрактальной геометрии и слова фрактал. Работая в IBM математическим аналитиком, он изучал шумы в электронных схемах, которые невозможно было описать с помощью статистики. Постепенно сопоставив факты, он пришел к открытию нового направления в математике - фрактальной геометрии.
Этот ученый стал знаменит благодаря основанию и дальнейшим исследования фрактальной геометрии. В 1993 году он стал лауреатом премии Вольфа по физике.
Бенуа Мандельброт был рожден в 1924 году в Варшаве. В 1936 году его семья уезжает в Париж, где юный Бенуа попадает под влияние своего дяди Шолема Мандельбройта, бывшего известным математиком, входящим в группу математиков с общим псевдонимом «Николя Бурбаки».
Что же такое фрактал. Сам Мандельброт вывел слово fractal от латинского слова fractus, что означает разбитый (поделенный на части). И одно из определений фрактала - это геометрическая фигура, состоящая из частей и которая может быть поделена на части, каждая из которых будет представлять уменьшенную копию целого (по крайней мере, приблизительно).
Чтобы представить себе фрактал понаглядней рассмотрим пример, приведенный в книге Б.Мандельброта "The Fractal Geometry of Nature" ("Фрактальная геометрия природы") ставший классическим - "Какова длина берега Британии?".
Ответ на этот вопрос не так прост, как кажется. Все зависит от длины инструмента, которым мы будем пользоваться. Померив берег с помощью километровой линейки мы получим какую-то длину. Однако мы пропустим много небольших заливчиков и полуостровков, которые по размеру намного меньше нашей линейки. Уменьшив размер линейки до, скажем, 1 метра - мы учтем эти детали ландшафта, и, соответственно длина берега станет больше. Пойдем дальше и измерим длину берега с помощью миллиметровой линейки, мы тут учтем детали, которые больше миллиметра, длина будет еще больше. В итоге ответ на такой, казалось бы, простой вопрос может поставить в тупик кого угодно - длина берега Британии бесконечна.
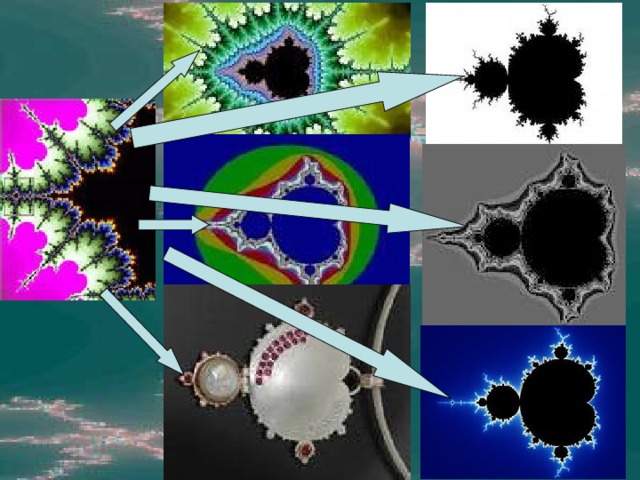
Фракталы делятся на группы. Самые большие группы это:
- геометрические фракталы
- алгебраические фракталы
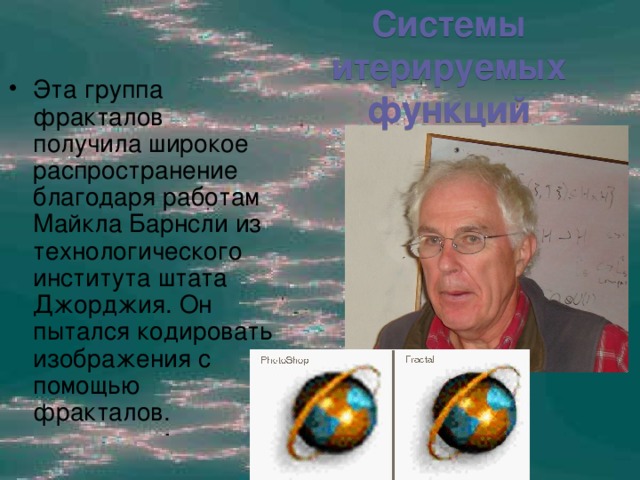
- системы итерируемых функций
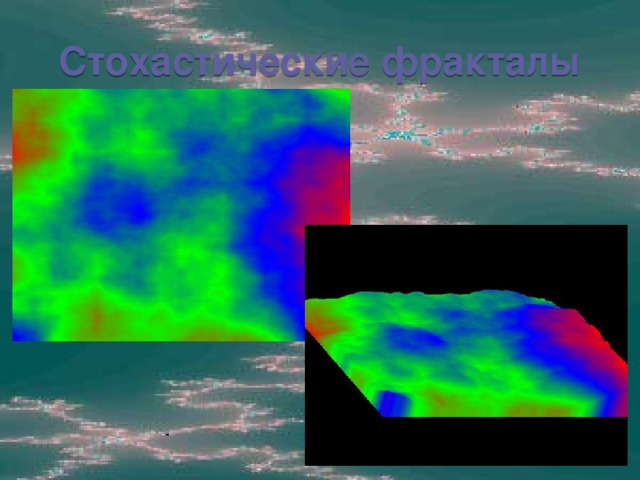
- стохастические фракталы.
Естественные науки
В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
Фрактальные антенны
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.
Сжатие изображений
Существуют алгоритмы сжатия изображения с помощью фракталов. Они основаны на идее о том, что вместо самого изображения можно хранить сжимающее отображение, для которого это изображение (или некоторое близкое к нему) является неподвижной точкой. Один из вариантов данного алгоритма был использован фирмой Microsoft при издании своей энциклопедии, но большого распространения эти алгоритмы не получили.
Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений
Децентрализованные сети
Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.
Экономика и финансы
А. А. Алмазов в своей книге «Фрактальная теория. Как поменять взгляд на рынки» предложил способ использования фракталов при анализе биржевых котировок, в частности — на рынке Форекс