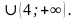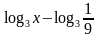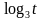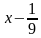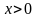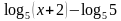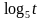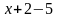В зависимости от УМК разработка может быть использована на уроках в 10-ом или в 11-ом классе (в профильных группах), а также при прохожднии дополнительных курсов.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Решение неравенств с использованием метода рационализации.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Решение неравенств с использованием метода рационализации.»
Полезное для учителя
Распродажа видеоуроков!
2340 руб.
3340 руб.
2000 руб.
2860 руб.
1970 руб.
2820 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
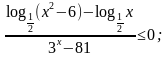 б)
б) 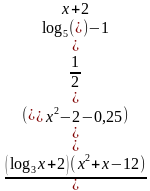 .
.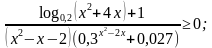 б)
б) 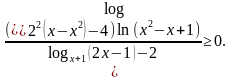
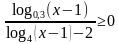 , б)
, б) 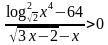 , в)
, в) 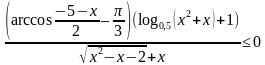 .
. 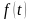 определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству
определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству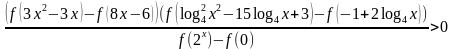 .
. 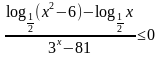

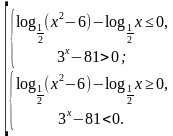
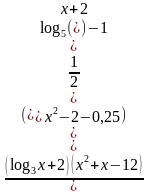 ?
?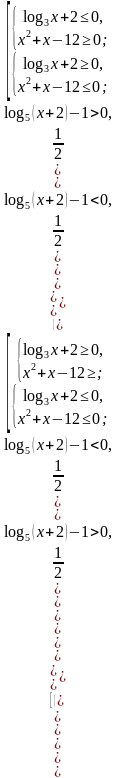
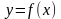 называется возрастающей, если для
называется возрастающей, если для 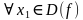 и
и 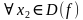 имеет место
имеет место 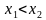

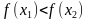 .
.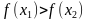 .
.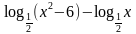
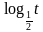
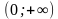
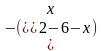
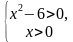
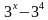
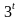
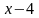
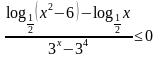
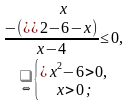
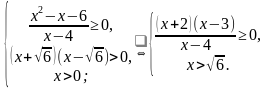
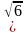 ;3]
;3]