По дидактической цели - это урок обобщения и систематизации знаний, а по способу проведения - фронтальная и индивидуальная работа в сочетании с разными видами самостоятельной деятельности.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Конспект урока по теме "Преобразование выражений с использованием формул сокращенного умножения"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Конспект урока по теме "Преобразование выражений с использованием формул сокращенного умножения"»
Полезное для учителя
Распродажа видеоуроков!
1670 руб.
2780 руб.
1570 руб.
2620 руб.
1570 руб.
2620 руб.
1670 руб.
2780 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
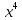 = (2
= (2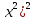 ; в) 36
; в) 36 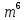 =(6
=(6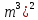 .
.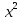 -5)(
-5)(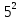 =
= 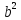 )(
)(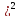 -(
-(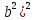 =81
=81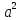 -
-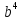 .
.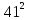 -
-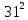 =(41-31)(41+31)= 10
=(41-31)(41+31)= 10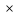 72=720;
72=720;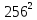 -
-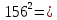 (256-156)(256+156)=100
(256-156)(256+156)=100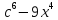 =(
=(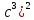 - (
- (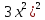 =(
=(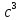 -
-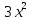 )(
)(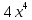 -
- 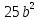 = (
= (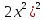 -(5b
-(5b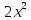 -5b)(
-5b)(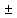 b
b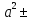 2ab+
2ab+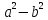 =( a-b)(a+b)
=( a-b)(a+b)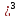 =
=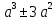 b+
b+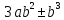 , учащиеся проговаривают их.
, учащиеся проговаривают их.















