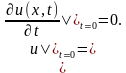Волновые процессы, происходящие в твердых волноводах
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Статья по математике на тему "Волновые процессы, происходящие в твердых волноводах"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Статья по математике на тему "Волновые процессы, происходящие в твердых волноводах"»
Полезное для учителя
Распродажа видеоуроков!
2040 руб.
2920 руб.
1830 руб.
2620 руб.
1650 руб.
2350 руб.
1950 руб.
2780 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
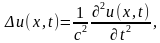
 – оператор Лапласа,
– оператор Лапласа, 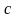 – фазовая скорость, с начальными условиями
– фазовая скорость, с начальными условиями 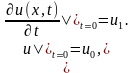
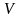 , ограниченный поверхностью
, ограниченный поверхностью 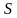 . В результате деформации под воздействием поверхностных сил точки тела
. В результате деформации под воздействием поверхностных сил точки тела 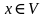 отклоняются на величину, которая характеризуется вектором перемещения
отклоняются на величину, которая характеризуется вектором перемещения 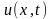 . Вектор перемещения характеризуется отклонением каждой точки тела от начального положения. Функция
. Вектор перемещения характеризуется отклонением каждой точки тела от начального положения. Функция 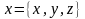 и времени
и времени 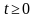 .
. 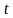 описывается множителем
описывается множителем 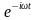 . Задача нахождения колебаний системы, которая описывается волновым уравнением, приводит к нахождению решений уравнения Гельмгольца, получающееся подстановкой в волновое уравнение функции
. Задача нахождения колебаний системы, которая описывается волновым уравнением, приводит к нахождению решений уравнения Гельмгольца, получающееся подстановкой в волновое уравнение функции 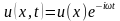 . Уравнение примет вид
. Уравнение примет вид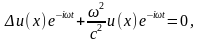
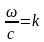 – волновое число.
– волновое число.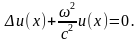
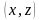 . Решение
. Решение 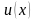 зависит только от двух пространственных координат
зависит только от двух пространственных координат 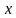 и
и 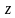
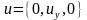 .
.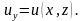 Кроме того, к работе предполагается, что начальные условия по времени равняются нулю
Кроме того, к работе предполагается, что начальные условия по времени равняются нулю