ТЕМА УРОКА:
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ОРТОГОНАЛЬНОГО ЧЕРТЕЖА: СПОСОБ ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ И СПОСОБ ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ.
10 класс
учитель черчения
Дементьева И.П .

ЦЕЛЬ УРОКА:
- Обучающая – ознакомить учащихся со способами преобразования ортогонального чертежа: способами плоскопараллельного перемещения и замены плоскостей проекций, научить учащихся пользоваться методами преобразования проекций при решении задач.
- Развивающая – развивать творческое и логическое мышление, пространственное воображение.
- Воспитательная – формирование самостоятельности, воспитание познавательного интереса к предмету, внимания, аккуратности при выполнении чертежей, дисциплинированности.

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ ОПОРНЫЙ КОНСПЕКТ:
- Основные свойства параллельного проецирования:
- 1. Свойство однозначности. Проекцией точки на плоскость есть точка.
- 2. Свойство прямолинейности. Проекцией прямой линии на плоскость есть прямая.
- 3. Свойство принадлежности . Если точка принадлежит линии, то проекция точки
принадлежит проекции этой линии.
- 4. Свойство сохранения параллельности . Проекциями параллельных прямых являются
параллельные прямые.
- 5. Свойство деления отрезка в отношении . Если отрезок прямой линии делится
точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в
том же отношении.
- 6. Свойство параллельного переноса . Проекция фигуры не меняется при параллельном переносе плоскости проекций.
ВЫВОД : три последние свойства обеспечивают более простое построение
изображения и меньше искажают форму и размеры оригинала
по сравнению с центральной проекцией.
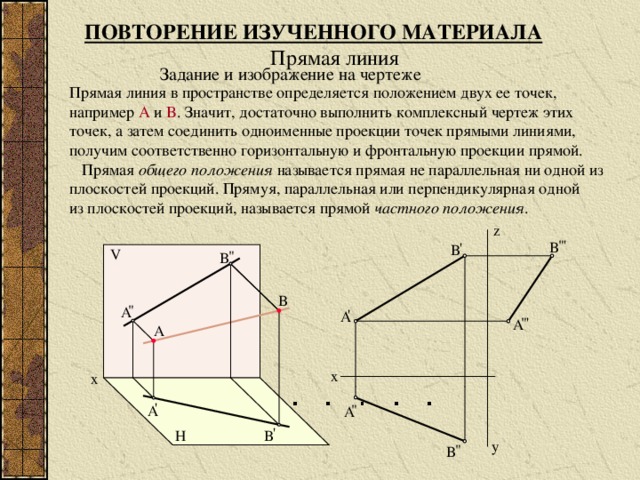
ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
Прямая линия
Задание и изображение на чертеже
Прямая линия в пространстве определяется положением двух ее точек,
например А и B . Значит, достаточно выполнить комплексный чертеж этих
точек, а затем соединить одноименные проекции точек прямыми линиями,
получим соответственно горизонтальную и фронтальную проекции прямой.
Прямая общего положения называется прямая не параллельная ни одной из
плоскостей проекций. Прямуя, параллельная или перпендикулярная одной
из плоскостей проекций, называется прямой частного положения .
z
"
'
B
'
B
V
"
B
B
"
A
'
A
"
'
A
A
x
x
'
"
A
A
'
B
H
y
"
B
= н.в.
= н.в.
= н.в.
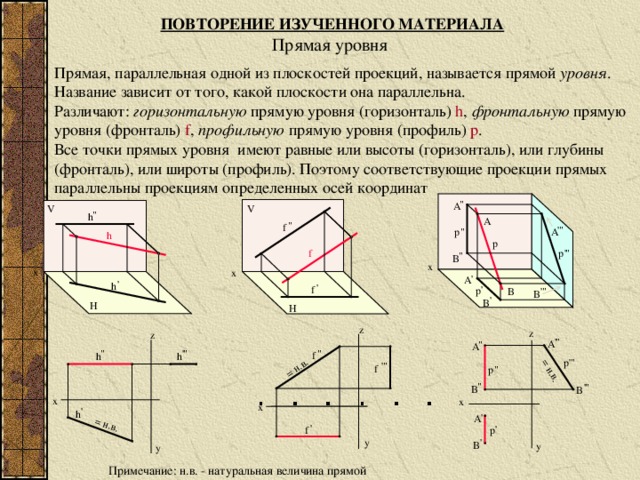
ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
Прямая уровня
Прямая, параллельная одной из плоскостей проекций, называется прямой уровня .
Название зависит от того, какой плоскости она параллельна.
Различают: горизонтальную прямую уровня (горизонталь) h , фронтальную прямую
уровня (фронталь) f , профильную прямую уровня (профиль) p .
Все точки прямых уровня имеют равные или высоты (горизонталь), или глубины
(фронталь), или широты (профиль). Поэтому соответствующие проекции прямых
параллельны проекциям определенных осей координат
"
A
V
V
"
h
A
"
f
'
"
"
p
A
h
p
"
'
f
p
"
B
x
x
x
'
A
'
h
'
'
f
p
B
'
"
B
'
B
H
H
z
z
z
"
'
A
"
A
"
"
'
"
f
h
h
'
"
p
"
'
f
"
p
"
'
"
B
B
x
x
x
'
h
'
A
'
'
f
p
y
'
B
y
y
Примечание: н.в. - натуральная величина прямой

ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
Проецирующая прямая
Прямая, перпендикулярная какой- либо плоскости проекции, называется проецирующей .
Различают: горизонтально проецирующую ( AB ), фронтально проецирующую
( CD ) и профильно проецирующую ( EF ).
У проецирующей прямой одна проекция вырождается в точку, а две другие проекции
параллельны самой прямой и совпадают с направлением линии связи.
V
"
"
"
A
F
E
"
_
A
_
_
_
"
"
_
D
C
_
"
"
D
C
"
"
F
E
D
A
"
B
F
E
C
x
"
B
'
D
x
B
'
_
D
_
'
_
'
F
E
'
'
B
A
_
'
_
C
_
'
'
B
A
'
'
F
C
'
E
H

ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
Взаимное расположение точки и прямой
Из свойств параллельного проецирования (свойство принадлежности) известно, что если точка
лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой.
Поэтому, из четырех точек A , B , C и D , приведенных на чертеже, лишь одна точка А лежит на
прямой. Точка В находится над прямой, так как она расположена выше , чем горизонтально
конкурирующая с ней точка прямой a (фронтальная проекция этой точки прямой a отмечена
кстиком). Аналогично, точка С находится перед прямой a , точка D расположена ниже и дальше
точки прямой a .
Определение взаимного положения точки и профильной прямой выполняется с помощью
построения профильной проекции . На чертеже точка С расположена над и перед прямой AB .
z
'
"
"
A
B
"
A
"
C
"
"
'
C
"
D
C
"
A
p
'
p
"
a
"
"
"
B
'
"
B
x
'
A
'
D
'
С
p
'
'
a
B
'
y
'
B
'
C
'
A
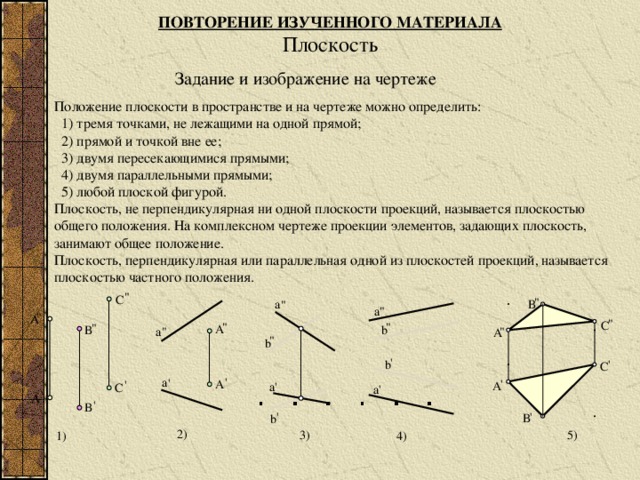
ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА
Плоскость
Задание и изображение на чертеже
Положение плоскости в пространстве и на чертеже можно определить:
1) тремя точками, не лежащими на одной прямой;
2) прямой и точкой вне ее;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми;
5) любой плоской фигурой.
Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью общего положения. На комплексном чертеже проекции элементов, задающих плоскость, занимают общее положение.
Плоскость, перпендикулярная или параллельная одной из плоскостей проекций, называется плоскостью частного положения.
"
C
"
B
a
"
a
"
"
A
"
C
"
"
"
A
b
B
a
"
"
A
"
b
'
b
'
C
'
a
'
'
A
'
A
a
'
C
a
'
'
A
'
B
'
'
B
b
2)
5)
3)
4)
1)
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА (МОТИВАЦИЯ): ЗАЧЕМ ПРЕОБРАЗОВЫВАТЬ ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ?
Трудности решения одной и той же задачи, если объект проецирования имеет общее положение, существенно зависят от положения геометрических объектов относительно плоскостей проекций.
Каким путем можно получить удобные проекции для решения поставленной задачи по заданным неудобным ортогональным проекциям?
Переход от общего положения геометрической фигуры к частному можно осуществлять за счет изменения взаимного положения проецируемой фигуры и плоскостей проекций.
При ортогональном проецировании это достигается двумя путями:
- Метод плоскопараллельного перемещения.
- Метод замены плоскостей проекций.
В чем принципиальное различие этих двух способов преобразования чертежа – метода замены плоскостей проекций и плоскопараллельного перемещения?
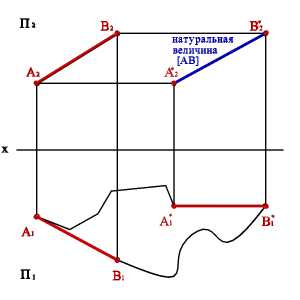
1. Перемещение в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве - метод плоскопараллельного перемещения.
2. Перемещение плоскостей проекций в новое положение по отношению, к которому проецируемая фигура (которая не меняет положения в пространстве) окажется в частном положении - метод замены плоскостей проекций.
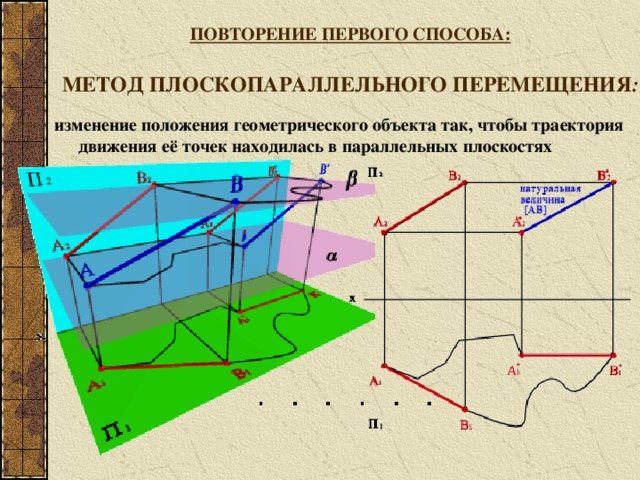
ПОВТОРЕНИЕ ПЕРВОГО СПОСОБА: МЕТОД ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ :
изменение положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях

ПОВТОРЕНИЕ ПЕРВОГО СПОСОБА: СВОЙСТВА ПЛОСКОПАРАЛЛЕЛЬНОГО ПЕРЕМЕЩЕНИЯ:
1. При всяком перемещении точек в плоскости параллельной плоскости П 1 , её фронтальная проекция перемещается по прямой линии, параллельной оси х .
2. В случае произвольного перемещения точки в плоскости параллельной П 2 , её горизонтальная проекция перемещается по прямой параллельной оси х .
В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой линии - определяющей траекторию перемещения точек, метод плоскопараллельного проецирования имеет следующие частные случаи:
1. Метод вращения вокруг оси, перпендикулярной плоскости проекций;
2. Метод вращения вокруг оси, параллельной плоскости проекций;
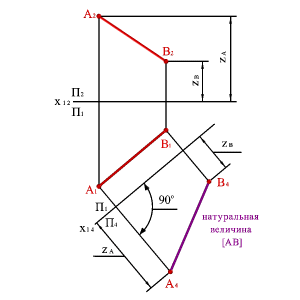
3. Метод вращения вокруг оси, принадлежащей плоскости проекций (вращение вокруг следа плоскости)- способ совмещения.
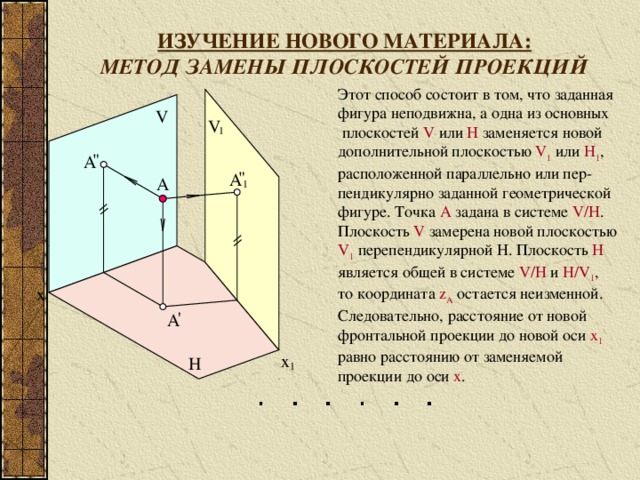
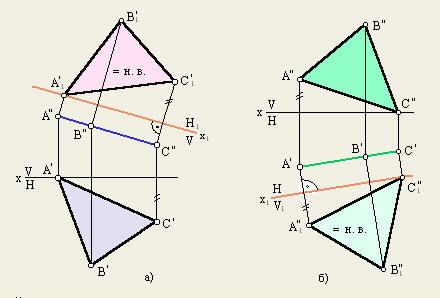
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА:
МЕТОД ЗАМЕНЫ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Этот способ состоит в том, что заданная
фигура неподвижна, а одна из основных
плоскостей V или H заменяется новой
дополнительной плоскостью V 1 или H 1 ,
расположенной параллельно или пер-
пендикулярно заданной геометрической
фигуре. Точка A задана в системе V/H .
Плоскость V замерена новой плоскостью
V 1 перепендикулярной H. Плоскость H
является общей в системе V/H и H/V 1 ,
то координата z A остается неизменной.
Следовательно, расстояние от новой
фронтальной проекции до новой оси x 1
равно расстоянию от заменяемой
проекции до оси x .
V
V
1
"
A
"
A
A
1
x
'
A
x
H
1
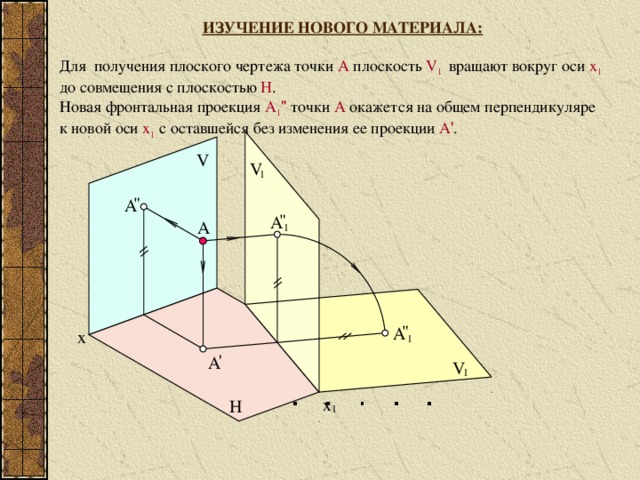
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА:
Для получения плоского чертежа точки А плоскость V 1 вращают вокруг оси x 1
до совмещения с плоскостью H .
Новая фронтальная проекция A 1 " точки А окажется на общем перпендикуляре
к новой оси x 1 с оставшейся без изменения ее проекции A ' .
V
V
1
"
A
"
A
A
1
"
A
x
1
'
A
V
1
x
H
1
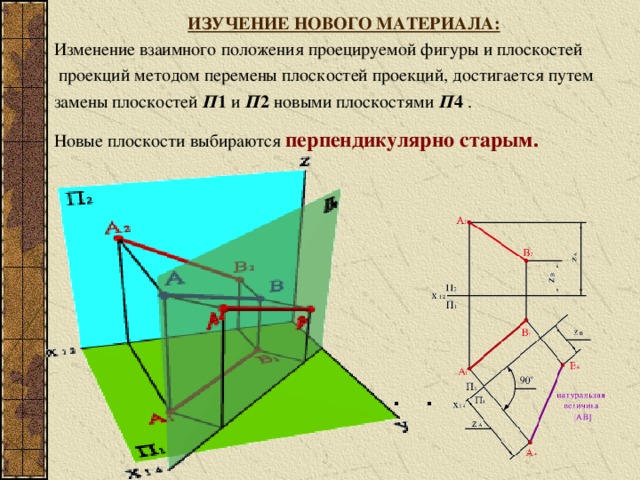
ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА:
Изменение взаимного положения проецируемой фигуры и плоскостей
проекций методом перемены плоскостей проекций, достигается путем
замены плоскостей П 1 и П 2 новыми плоскостями П 4 .
Новые плоскости выбираются перпендикулярно старым.
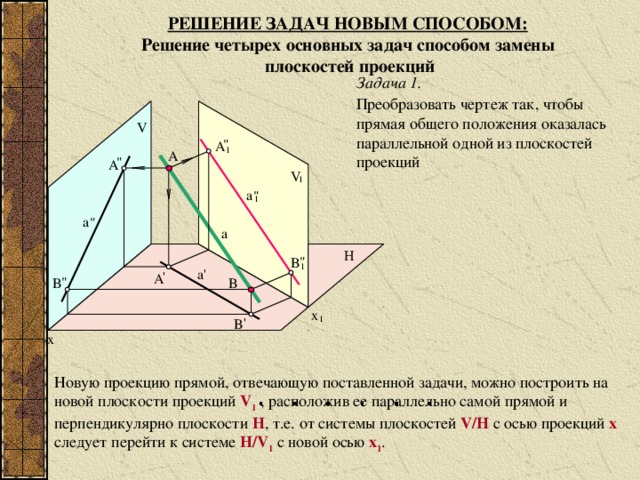
РЕШЕНИЕ ЗАДАЧ НОВЫМ СПОСОБОМ:
Решение четырех основных задач способом замены
плоскостей проекций
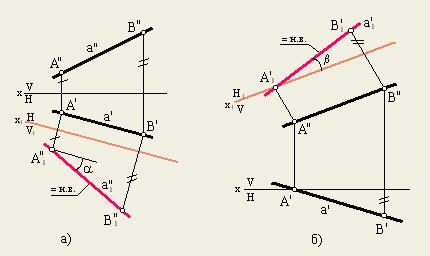
Задача 1.
Преобразовать чертеж так, чтобы
прямая общего положения оказалась
параллельной одной из плоскостей
проекций
V
"
A
1
A
"
A
V
1
a
"
1
a
"
a
H
"
B
1
a
'
'
A
"
B
B
x
1
'
B
x
Новую проекцию прямой, отвечающую поставленной задачи, можно построить на
новой плоскости проекций V 1 , расположив ее параллельно самой прямой и
перпендикулярно плоскости H , т.е. от системы плоскостей V/H с осью проекций x следует перейти к системе H/V 1 с новой осью x 1 .
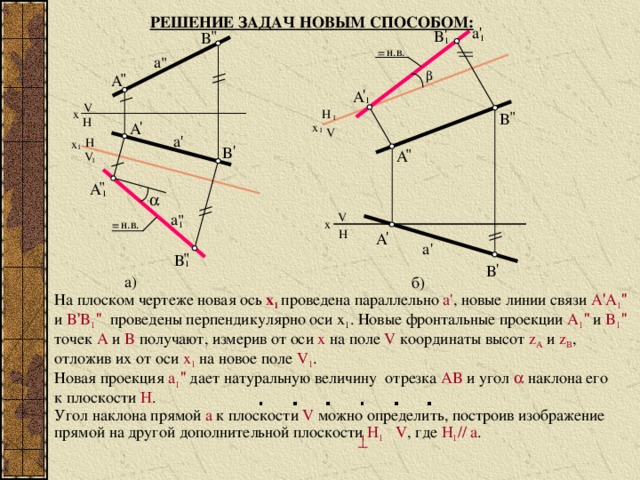
РЕШЕНИЕ ЗАДАЧ НОВЫМ СПОСОБОМ:
a
'
'
B
"
B
1
1
н.в.
=
a
"
"
A
'
A
1
V
x
H
"
B
1
H
'
A
x
V
1
a
'
H
x
'
B
1
"
A
V
1
"
A
1
V
a
"
x
н.в.
=
1
H
'
A
a
'
"
B
1
'
B
а)
б)
На плоском чертеже новая ось x 1 проведена параллельно a' , новые линии связи A ' A 1 "
и B ' B 1 " проведены перпендикулярно оси x 1 . Новые фронтальные проекции A 1 " и B 1 "
точек A и B получают, измерив от оси x на поле V координаты высот z A и z B ,
отложив их от оси x 1 на новое поле V 1 .
Новая проекция a 1 " дает натуральную величину отрезка AB и угол наклона его
к плоскости H .
Угол наклона прямой a к плоскости V можно определить, построив изображение
прямой на другой дополнительной плоскости H 1 V , где H 1 // a .
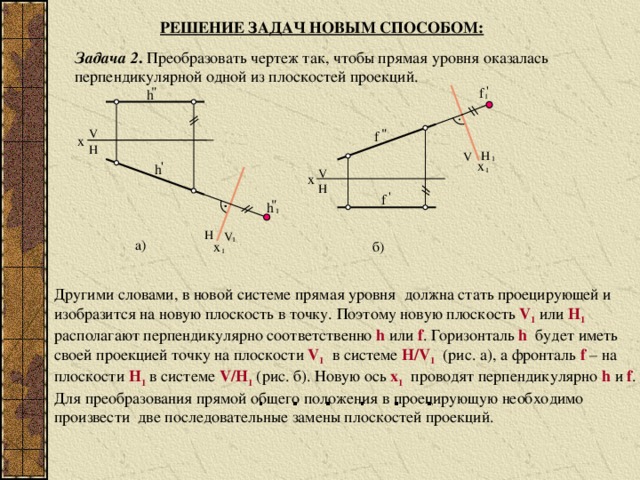
РЕШЕНИЕ ЗАДАЧ НОВЫМ СПОСОБОМ:
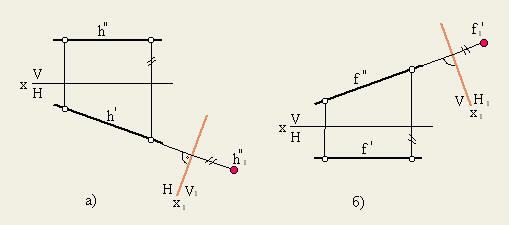
Задача 2 . Преобразовать чертеж так, чтобы прямая уровня оказалась
перпендикулярной одной из плоскостей проекций.
'
"
f
h
1
"
V
f
x
H
H
V
1
x
'
h
V
1
x
H
'
f
"
h
1
H
V
1
а)
б)
x
1
Другими словами, в новой системе прямая уровня должна стать проецирующей и
изобразится на новую плоскость в точку. Поэтому новую плоскость V 1 или H 1 располагают перпендикулярно соответственно h или f . Горизонталь h будет иметь своей проекцией точку на плоскости V 1 в системе H/V 1 (рис. а), а фронталь f – на плоскости H 1 в системе V/H 1 (рис. б). Новую ось x 1 проводят перпендикулярно h и f .
Для преобразования прямой общего положения в проецирующую необходимо произвести две последовательные замены плоскостей проекций.
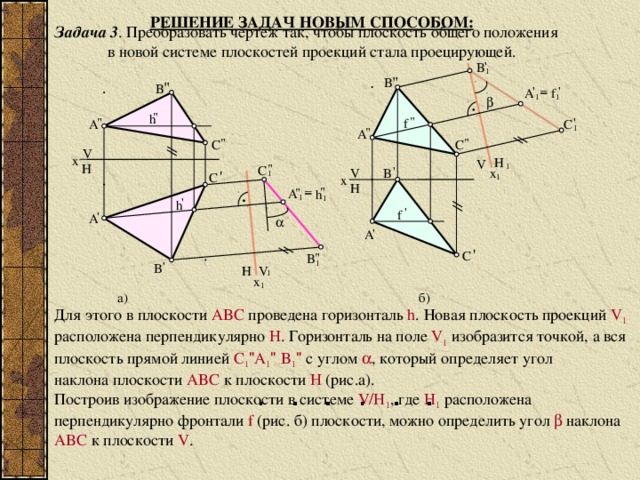
РЕШЕНИЕ ЗАДАЧ НОВЫМ СПОСОБОМ:
Задача 3 . Преобразовать чертеж так, чтобы плоскость общего положения
в новой системе плоскостей проекций стала проецирующей.
'
B
1
"
B
_
"
_
_
B
'
'
f
A
1
1
"
h
"
'
"
f
C
A
1
"
A
"
"
C
C
V
x
H
V
"
H
1
C
'
B
x
V
'
1
C
x
1
_
_
_
H
"
"
A
h
1
1
'
h
'
f
'
A
'
A
'
C
"
B
'
1
B
H
V
1
x
1
а)
б)
Для этого в плоскости ABC проведена горизонталь h . Новая плоскость проекций V 1
расположена перпендикулярно H . Горизонталь на поле V 1 изобразится точкой, а вся плоскость прямой линией C 1 " A 1 " B 1 " с углом , который определяет угол
наклона плоскости ABC к плоскости H (рис.а).
Построив изображение плоскости в системе V/H 1 , где H 1 расположена перпендикулярно фронтали f (рис. б) плоскости, можно определить угол наклона ABC к плоскости V .
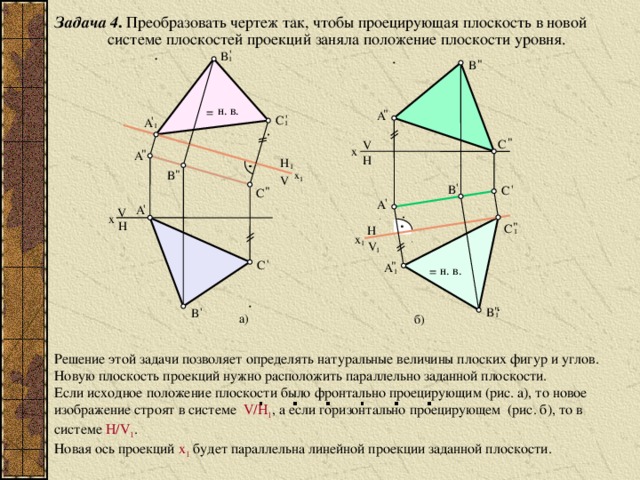
Задача 4 . Преобразовать чертеж так, чтобы проецирующая плоскость в новой
системе плоскостей проекций заняла положение плоскости уровня.
'
B
1
"
B
н. в.
=
"
A
'
C
'
A
1
1
"
C
V
x
"
A
H
H
1
"
B
x
V
1
'
B
'
C
"
C
'
A
'
A
V
x
H
"
C
H
1
x
V
1
1
'
C
"
A
н. в.
=
1
"
B
'
B
1
а)
б)
Решение этой задачи позволяет определять натуральные величины плоских фигур и углов.
Новую плоскость проекций нужно расположить параллельно заданной плоскости.
Если исходное положение плоскости было фронтально проецирующим (рис. а), то новое изображение строят в системе V/H 1 , а если горизонтально проецирующем (рис. б), то в системе H/V 1 .
Новая ось проекций x 1 будет параллельна линейной проекции заданной плоскости.

Вывод:
- Выбирая способ преобразования ортогонального чертежа, следует учитывать требования к компактности чертежа, четкость и возможную простоту графических операций.

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА: РЕШЕНИЕ ЗАДАЧ:
Задача №1.
Определить расстояние между двумя точками А и В, заданных координатами:
( Решение сводится к определению
натуральной величины отрезка АВ, то есть преобразование прямой общего положения в прямую уровня .)
x
А
45
y
В
z
5
5
10
20
15

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА: РЕШЕНИЕ ЗАДАЧ:
Задача №2.
Определить расстояние от точки К до прямой, заданной отрезком АВ:
(Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую, то есть преобразовать прямую общего положения АВ в проецирующую.)
x
А
45
y
В
К
z
15
5
20
15
10
0
30
20

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА: РЕШЕНИЕ ЗАДАЧ:
Задача №3.
Определить расстояние между двумя параллельными прямыми, заданными отрезками АВ и СК.
( Преобразовать прямые общего положения в проецирующие и замерить между ними расстояние . )
x
А
45
В
y
С
5
30
z
20
45
5
К
10
40
5
30
15
20

ДОМАШНЕЕ ЗАДАНИЕ:
- читать по электронному учебнику: глава 6.1, после главы пройти тесты.
- Задачи №1, №2, №3 решить при помощи второй линии уровня.