Методическая разработка занятия "Арифметические основы ЭВМ"

Арифметические основы построения ЭВМ

• Системы счисления.
• Правила перевода.
• Перевод из одной позиционной системы счисления в другую.
• Арифметические операции
• Перевод дробей и целых чисел.
• Представление чисел со знаком
• Кодирование чисел
• Представление числовых данных в памяти ЭВМ
• Представление символьных данных в памяти ЭВМ
• Контрольная работа по теме «Арифметические основы построения ЭВМ»

• Теоретическая часть
• Закрепление
• Домашнее задание
• Для учителя
• Дополнительные материалы

• Теоретическая часть
• Закрепление
• Домашнее задание
• Для учителя

Перевод из одной позиционной системы счисления в другую.

• Теоретическая часть
• Примеры
• Задание к практической работе
• Для учителя

• Вариант 1
• Вариант 2
• Вариант 3
• Вариант 4
• Вариант 5
• Вариант 6
• Вариант 7
• Вариант 8
• Вариант 9
• Вариант 10
• Вариант 11
• Вариант 12

• Вариант 13
• Вариант 14
• Вариант 15
• Вариант 16
• Вариант 17
• Вариант 18
• Вариант 19
• Вариант 20
• Вариант 21
• Вариант 22
• Вариант 23
• Вариант 24
• Вариант 25

• Теоретическая часть
• Примеры
• Задание к практической работе
• Для учителя

• Вариант 1
• Вариант 2
• Вариант 3
• Вариант 4
• Вариант 5
• Вариант 6
• Вариант 7
• Вариант 8
• Вариант 9
• Вариант 10
• Вариант 11
• Вариант 12

• Вариант 13
• Вариант 14
• Вариант 15
• Вариант 16
• Вариант 17
• Вариант 18
• Вариант 19
• Вариант 20
• Вариант 21
• Вариант 22
• Вариант 23
• Вариант 24
• Вариант 25

Перевод дробей и целых чисел.

• Теоретическая часть
• Закрепление
• Домашнее задание
• Для учителя

Представление чисел со знаком

• Теоретическая часть
• Закрепление
• Домашнее задание
• Для учителя

• Теоретическая часть
• Закрепление
• Домашнее задание
• Для учителя

Представление числовых данных в памяти ЭВМ

• Теоретическая часть
• Примеры
• Задание к практической работе
• Для учителя

• Вариант 13
• Вариант 14
• Вариант 15
• Вариант 16
• Вариант 17
• Вариант 18
• Вариант 19
• Вариант 20
• Вариант 21
• Вариант 22
• Вариант 23
• Вариант 24
• Вариант 25

• Вариант 1
• Вариант 2
• Вариант 3
• Вариант 4
• Вариант 5
• Вариант 6
• Вариант 7
• Вариант 8
• Вариант 9
• Вариант 10
• Вариант 11
• Вариант 12

Представление символьных данных в памяти ЭВМ

• Теоретическая часть
• Задание к практической работе
• Для учителя

• Вариант 13
• Вариант 14
• Вариант 15
• Вариант 16
• Вариант 17
• Вариант 18
• Вариант 19
• Вариант 20
• Вариант 21
• Вариант 22
• Вариант 23
• Вариант 24
• Вариант 25

• Вариант 1
• Вариант 2
• Вариант 3
• Вариант 4
• Вариант 5
• Вариант 6
• Вариант 7
• Вариант 8
• Вариант 9
• Вариант 10
• Вариант 11
• Вариант 12

Контрольная работа по теме «Арифметические основы построения ЭВМ»

• Вариант 1
• Вариант 2
• Для учителя

• В повседневной практике для представления чисел люди пользуются почти исключительно десятичной системой счисления. Лишь в редких случаях встречаются остатки других систем - римский счет, двенадцатеричная система (часы), шестидесятеричная (минуты).
• Однако система изображения чисел, которая веками складывалась применительно к ручному труду, не позволяет получить наиболее эффективные методы выполнения вычислений. По этой причине в вычислительной технике применяются другие системы счисления и чаще всего - двоичная. Введем несколько определений.
• Cистема счисления - совокупность символов и правил для обозначения чисел.
• Разделяют системы счисления позиционные и непозиционные. Непозиционная система счисления задается перечислением изображаемых в ней значений. Позиционная система счисления характеризуется основанием и тем, что числа, как правило, представляются несколькими разрядами (являются многоразрядными), а вес любого разряда определяется его позицией в числе.

• Oснование позиционной системы счисления определяет количество различных цифр (символов), допустимое в системе счисления. Это же число определяет, во сколько раз вес цифры данного разряда меньше веса цифры соседнего старшего разряда.
• Так, в десятичной системе счисления, основание которой равно 10, различают 10 арабских цифр - 0, 1, 2, ..., 9.
• Следовательно, при ее использовании для записи числа, не превышающего девяти, достаточно одной цифры, и такое число записывается как одноразрядное. А в случае записи числа, большего девяти, оно представляется как многоразрядное. При этом вес каждого более старшего (расположенного слева от текущего) разряда в десять (основание системы счисления) раз больше текущего.

• Так, например, число 359 - трехразрядное, и в нем 9 - цифра разряда единиц, 5 - цифра разряда десятков, 3 - цифра разряда сотен (в 10 раз превышает вес разряда десятков). При этом значение трехразрядного числа 359 получается суммированием трех слагаемых : 3 сотни + 5 десятков + 9 единиц.
• Общее правило определения веса разряда многоразрядного числа таково:
• Если пронумеровать разряды целого числа справа налево, начиная от 0 для разряда единиц, то вес любого разряда получается возведением основания системы счисления в степень, значение которой равно номеру разряда.
• Так, вес самого младшего разряда целых чисел равен 1, поскольку номер разряда равен 0, а любое число, в том числе и число 10, возведенное в нулевую степень, дает в результате единицу. Вес следующего слева разряда равен 10 в степени 1, т.е. равен десяти, и т.д.

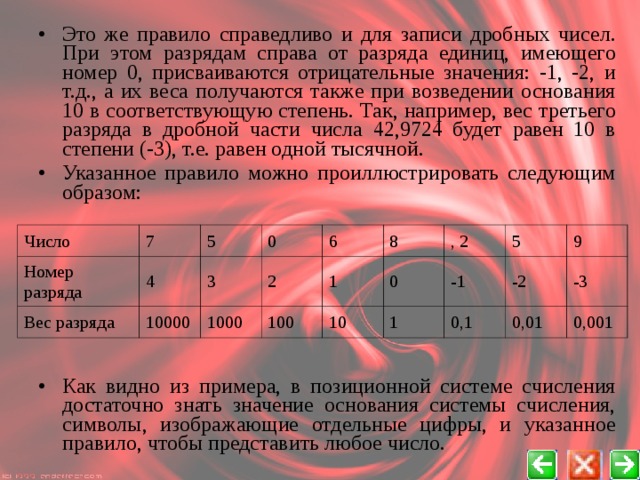
• Это же правило справедливо и для записи дробных чисел. При этом разрядам справа от разряда единиц, имеющего номер 0, присваиваются отрицательные значения: -1, -2, и т.д., а их веса получаются также при возведении основания 10 в соответствующую степень. Так, например, вес третьего разряда в дробной части числа 42,9724 будет равен 10 в степени (-3), т.е. равен одной тысячной.
• Указанное правило можно проиллюстрировать следующим образом:

• Как видно из примера, в позиционной системе счисления достаточно знать значение основания системы счисления, символы, изображающие отдельные цифры, и указанное правило, чтобы представить любое число.

Число

Номер разряда

7

Вес разряда

5

4

0

3

10000

6

1000

2

100

1

8

10

, 2

0

-1

5

1

-2

9

0,1

-3

0,01

0,001

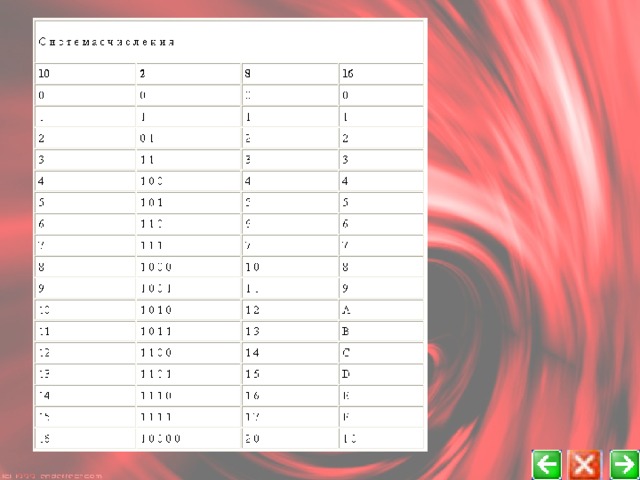
• В вычислительной технике широко применяют двоичную, восьмеричную и шестнадцатиричную систему счисления.
• Двоичная система счисления имеет основание 2, и, следовательно, две разных цифры - 0 и 1; восьмеричная - восемь разных цифр - 0, 1, 2, 3, 4, 5, 6, 7, а шестнадцатеричная - шестнадцать цифр - десять арабских цифр от 0 до 9 и еще шесть символов -
• А (цифра, изображающая десять), D (цифра тринадцать),
• В (цифра одиннадцать), E (цифра четырнадцать),
• С (цифра двенадцать), F (цифра пятнадцать).
• Проще всего сопоставить запись одних и тех же чисел в этих системах счисления можно с использованием таблицы 1, приведенной на следующей странице.

• Мы уже говорили о том, что современные цифровые ЭВМ все используют в качестве основной двоичную систему счисления. К ее достоинствам относится:
• простота выполнения арифметических и логических операций, что влечет за собой простоту устройств, реализующих эти операции;
• возможность использования аппарата алгебры логики (булевой алгебры) для анализа и синтеза операционных устройств ЭВМ.
• К неудобствам двоичной системы счисления относится необходимость перевода чисел из десятичной в двоичную и наоборот, а также то, что запись числа в двоичной системе громоздка (требует большего числа разрядов, чем привычная для человека десятичная). По этой и ряду других причин, кроме двоичной применяются восьмеричная и шестнадцатеричная системы счисления.
• Совместное использование указанных систем обусловлено двумя причинами:
• в восьмеричной и шестнадцатиричной системах любое число записывается более компактно, нежели двоичное;
• простотой преобразования из двоичной в восьмеричную (шестнадцатиричную) систему счисления и наоборот.

• Представление 2-ичного числа
• Тип системы счисления
• Представление 16-ичного числа

• В коробке лежит 31 8 шар. Среди них 12 8 красных и 17 8 желтых. Докажите, что здесь нет ошибки.
• В классе 1111 2 девочек и 1010 2 мальчиков. Сколько учеников в классе?
• Перевести в десятичную систему счисления следующие числа: 34 8 , 110011 2 , 11 01 2 , 1АВС 1 6 .
• В бумагах чудака-математика была найдена его автобиография. Начиналась она следующими удивительными словами: «Я окончил курс университета 44 лет отроду. Спустя год, 100-летним молодым челове­ком, я женился на 34-летней девушке. Незначительная разница в возрасте - всего 11 лет - способствовала тому, что мы жили общими ин­тересами и мечтами. Спустя немного лет у меня уже была маленькая семья из 10 детей. Жалованья я получал в месяц всего 200 рублей, из которых 1/10 приходилось отдавать сестре, так что мы с детьми жили на 130 рублей в месяц». Чем объяснить странные противоречия в числах приведенной биографии? Переведите эту биографию в десятичную систему счисления.

2c/c” При переводе многоразрядного числа каждую цифру исходного восьмеричного числа представить всегда точно тремя двоичными цифрами, взятыми из приведенной выше таблицы. При этом, если для записи соответствующей восьмеричной цифры в виде двоичной требуется менее трех двоичных цифр, двоичный эквивалент дополняется слева нулями (незначащие нули не исказят значения числа). Таким образом, например, при записи четырехразрядного восьмеричного числа должно получиться двенадцатиразрядное двоичное. После окончания такого преобразования можно отбросить старшие для всего числа незначащие двоичные цифры. Отметим, что три цифры принято называть триадой . Поэтому можно сказать, что при описываемом переводе каждая восьмеричная цифра заменяется соответствующей ей триадой двоичных цифр. Если исходное число дробное, т.е. имеет целую и дробную часть, то в двоичном числе запятая ставится между триадами, представляющими соответствующие цифры исходного числа." width="640"

• Приведем правила перевода чисел из двоичной системы в восьмеричную (шестнадцатиричную) и наоборот.
• Правило перевода “8с/с - 2c/c”
• При переводе многоразрядного числа каждую цифру исходного восьмеричного числа представить всегда точно тремя двоичными цифрами, взятыми из приведенной выше таблицы. При этом, если для записи соответствующей восьмеричной цифры в виде двоичной требуется менее трех двоичных цифр, двоичный эквивалент дополняется слева нулями (незначащие нули не исказят значения числа). Таким образом, например, при записи четырехразрядного восьмеричного числа должно получиться двенадцатиразрядное двоичное. После окончания такого преобразования можно отбросить старшие для всего числа незначащие двоичные цифры.
• Отметим, что три цифры принято называть триадой . Поэтому можно сказать, что при описываемом переводе каждая восьмеричная цифра заменяется соответствующей ей триадой двоичных цифр.
• Если исходное число дробное, т.е. имеет целую и дробную часть, то в двоичном числе запятая ставится между триадами, представляющими соответствующие цифры исходного числа.

011 7 -- 111 1 -- 001 6 -- 110 2 -- 010 Теперь можно записать число в двоичной форме (для наглядности между триадами поместим пробелы): 371,62 - 011 111 001 , 110 010 И, наконец, запишем полученное двоичное число так, как это принято в математике, без незначащих нулей, а также отбросив правые нули в дробной части числа: 371,62 - 11111001,11001" width="640"

• Пример. Преобразуем восьмеричное число 371,62.
• Для этого запишем для каждой цифры соответствующую триаду:
• 3 -- 011
• 7 -- 111
• 1 -- 001
• 6 -- 110
• 2 -- 010
• Теперь можно записать число в двоичной форме (для наглядности между триадами поместим пробелы): 371,62 - 011 111 001 , 110 010
• И, наконец, запишем полученное двоичное число так, как это принято в математике, без незначащих нулей, а также отбросив правые нули в дробной части числа: 371,62 - 11111001,11001

8c/c” При переводе многоразрядного двоичного числа в восьмеричную форму поступают следующим образом: Исходное число разбивают на триады. При этом для целой части числа разбиение проводят от местонахождения запятой влево, а для дробной части - от этого же места вправо. Затем самая левая группа при необходимости дополняется незначащими нулями до образования триады, а самая правая группа только в дробной части дополняется нулями справа также до образования полной триады. После этого каждая триада заменяется соответствующей восьмеричной цифрой. Местоположение запятой сохраняется по тем же правилам, что и в правиле перевода “8с/с - 2c/c”" width="640"

• Правило перевода “2с/с - 8c/c”
• При переводе многоразрядного двоичного числа в восьмеричную форму поступают следующим образом: Исходное число разбивают на триады. При этом для целой части числа разбиение проводят от местонахождения запятой влево, а для дробной части - от этого же места вправо. Затем самая левая группа при необходимости дополняется незначащими нулями до образования триады, а самая правая группа только в дробной части дополняется нулями справа также до образования полной триады. После этого каждая триада заменяется соответствующей восьмеричной цифрой. Местоположение запятой сохраняется по тем же правилам, что и в правиле перевода “8с/с - 2c/c”

154,372" width="640"

• Пример. Представить двоичное число 1101100,01111101 в форме восьмеричного .
• Разобьем исходное число на группы по три цифры, приняв в качестве точки отсчета местоположение запятой (для наглядности между триадами поместим пробелы):
• 1 101 100 , 011 111 01
• Теперь дополним до трех цифр нулями самую левую группу слева и самую правую группу справа: 001 101 100 , 011 111 010
• И, наконец, заменим каждую триаду соответствующей восьмеричной цифрой: 001 101 100 , 011 111 100 -- 154,372

2c/c” При переводе многоразрядного шестнадцатиричного числа в двоичную форму каждую цифру исходного числа заменяют группой точно из четырех двоичных цифр (заменяют тетрадой двоичных цифр). Местоположение запятой сохраняется по тем же правилам, что и в правиле перевода “8с/с - 2c/c” В окончательной записи можно отбросить самые левые (незначащие) нули и самые правые нули дробной части. Пример. Преобразовать шестнадцатиричное число “6C,7D” в двоичную форму. Для этого запишем для каждой цифры соответствующую тетраду: 6 -- 0110 C -- 1100 7 -- 0111 D -- 1101 Теперь можно записать число в двоичной форме (для наглядности между тетрадами поместим пробелы): 6C,7D - 0110 1100 , 0111 1101 И, наконец, запишем полученное двоичное число так, как это принято в математике, без незначащих нулей: 6C,7D - 1101100,01111101" width="640"

• Правило перевода “16с/с - 2c/c”
• При переводе многоразрядного шестнадцатиричного числа в двоичную форму каждую цифру исходного числа заменяют группой точно из четырех двоичных цифр (заменяют тетрадой двоичных цифр). Местоположение запятой сохраняется по тем же правилам, что и в правиле перевода “8с/с - 2c/c” В окончательной записи можно отбросить самые левые (незначащие) нули и самые правые нули дробной части.
• Пример. Преобразовать шестнадцатиричное число “6C,7D” в двоичную форму. Для этого запишем для каждой цифры соответствующую тетраду:
• 6 -- 0110
• C -- 1100
• 7 -- 0111
• D -- 1101
• Теперь можно записать число в двоичной форме (для наглядности между тетрадами поместим пробелы): 6C,7D - 0110 1100 , 0111 1101
• И, наконец, запишем полученное двоичное число так, как это принято в математике, без незначащих нулей: 6C,7D - 1101100,01111101

16c/c” При переводе многоразрядного двоичного числа в шестнадцатиричную форму поступают следующим образом. Исходное число разбивают на тетрады. При этом для целой части числа разбиение проводят от местонахождения запятой влево, а для дробной части от этого же места вправо. Затем самая левая группа при необходимости дополняется незначащими нулями до образования тетрады, а самая правая группа только в дробной части дополняется нулями справа также до образования полной тетрады. После этого каждая тетрада заменяется соответствующей шестнадцатиричной цифрой. Местоположение запятой сохраняется по тем же правилам, что и в правиле перевода “8с/с - 2c/c”" width="640"

• Правило перевода “2с/с - 16c/c”
• При переводе многоразрядного двоичного числа в шестнадцатиричную форму поступают следующим образом. Исходное число разбивают на тетрады. При этом для целой части числа разбиение проводят от местонахождения запятой влево, а для дробной части от этого же места вправо. Затем самая левая группа при необходимости дополняется незначащими нулями до образования тетрады, а самая правая группа только в дробной части дополняется нулями справа также до образования полной тетрады. После этого каждая тетрада заменяется соответствующей шестнадцатиричной цифрой. Местоположение запятой сохраняется по тем же правилам, что и в правиле перевода “8с/с - 2c/c”

6С,7D. Шестнадцатеричная и восьмеричная системы счисления используются для более компактной и удобной записи двоичных чисел. Так, известность шестнадцатеричной системе принесло то, что с ее использованием удобно представлять программы в кодах большинства современных ЭВМ." width="640"

• Пример. Представить двоичное число 1101100,01111101 в форме шестнадцатеричного.
• Разобьем исходное число на группы по четыре цифры, приняв в качестве точки отсчета местоположение запятой (для наглядности между тетрадами поместим пробелы): 110 1100 , 0111 1101
• Теперь дополним до четырех цифр нулями слева самую левую группу: 0110 1100 , 0111 1101
• И, наконец, заменим каждую тетраду соответствующей шестнадцатеричной цифрой: 0110 1100 , 0111 1101 - 6С,7D.
• Шестнадцатеричная и восьмеричная системы счисления используются для более компактной и удобной записи двоичных чисел.
• Так, известность шестнадцатеричной системе принесло то, что с ее использованием удобно представлять программы в кодах большинства современных ЭВМ.

• Переведите число 2004 10 в:

• A) двоичную систему счисления;
• Б) восьмеричную систему счисления;
• B) шестнадцатеричную;

• Составьте свою биографию, записав все числа в двоичной системе счисления.
• Перевести числа 11110111011; 101010101; 111111 в шестнадцатеричную систему счисления
• Перевести числа 0,111011011; 0,000110101; 0,0101010111 - в восьмеричную систему счисления
• Перевести числа 0,00110011; 0,11100011101; 0,011011011 - в шестнадцатеричную систему счисления

1 обычно используют следующий алгоритм: 1) если переводится целая часть числа, то она делится на Р, после чего запоминается остаток от деления. Полученное частное вновь делится на Р, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на Р выписываются в порядке, обратном их получению; 2) если переводится дробная часть числа, то она умножается на Р, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на Р и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием Р." width="640"

• При переводе чисел из десятичной системы счисления в систему с основанием Р 1 обычно используют следующий алгоритм:
• 1) если переводится целая часть числа, то она делится на Р, после чего запоминается остаток от деления. Полученное частное вновь делится на Р, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на Р выписываются в порядке, обратном их получению;
• 2) если переводится дробная часть числа, то она умножается на Р, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на Р и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием Р.

• Пример 1. Перевести данное число из десятичной системы счисления в двоичную (получить пять знаков после запятой в двоичном представлении),
• а) 464 (10) ;
• б) 380,1875 (10) ;
• в) 115,94 (10)
• Решение:
• а) 464(10)= 111010000 (2) ;
• б) 380,1875(10) = 101111100,0011 (2) ;
• в) 115,94(10) - 1110011,11110 (2)
• (в данном случае было получено шесть знаков после запятой, после чего результат был округлен).

• Если необходимо перевести число из двоичной системы счисления в систему счисления, основанием которой является степень двойки, достаточно объединить цифры двоичного числа в группы по столько цифр, каков показатель степени, и использовать приведенный ниже алгоритм. Например, если перевод осуществляется в восьмеричную систему, то группы будут содержать три цифры (8 = 2 3 ). В целой части числа группировка производится справа налево, в дробной части — слева направо. Если в последней группе недостает цифр, дописываются нули: в целой части — слева, в дробной — справа. Затем каждая группа заменяется соответствующей цифрой новой системы. Соответствия приведены в таблице.

• При переводе чисел из системы счисления с основанием Р в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо (начальный номер — 1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда. Это и есть представление исходного числа в десятичной системе счисления.

• Пример 2. Перевести данное число в десятичную систему счисления:
• а) 1000001 (2) .
• 1000001 (2) = 1*2 6 +0*2 5 +0*2 4 +0*2 3 +0*2 2 +0*2 1 + 1*2 0 =64 + 1 = 65 (10)
• Замечание. Если в каком-либо разряде стоит нуль, то соответствующее слагаемое можно опускать;
• б)1000011111,0101 (2) .
• 1000011111,0101 (2) = 1*2 9 + 1*2 4 + 1*2 3 + 1*2 2 + 1*2 1 + 1*2 0 + 1*2 -2 + 1*2 -4 = 512+16 + 8 + 4 + 2+1+ 0,25 + 0,0625 = 543,3125 (10) ;
• в)1216,04 (8) .
• 1216,04 (8) = 1*8 3 + 2*8 2 + 1*8 1 + 6*8 0 + 4*8 -2 = 512 + 128 + 8 +6 + 0,0625 = 654,0625 (10) ;
• г)29А,5 (16) .
• 29А,5 (16) = 2*16 2 + 9*16 1 + 10*16 0 + 5*16 -1 = 512 + 144 + 10 + 0,3125 = 656,3125 (10) .

Задания к практической работе

• 1.Переведите данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.
• 2. Переведите данное число в десятичную систему счисления.

Вариант 1

• Задание 1
• а)860 (10) ;
• б)785 (10) ;
• в)149,375 (10) ;
• г) 953,25 (10) ;
• д) 228,79 (10)
• Задание 2
• а)1001010 (2) ;
• б) 1100111 (2) ;
• в) 110101101,00011 (2) ;
• г)111111100,0001 (2) ;
• д) 775,11 (8) ;
• е) 294,3 (16) .

Вариант 2

• Задание 1
• а) 250 (10) ;
• б) 757 (10) ;
• в) 711,25 (10) ;
• г) 914,625 (10) ;
• д) 261,78 (10) .
• Задание 2
• а) 1111000 (2) ;
• б) 1111000000 (2) ;
• в) 111101100,01101 (2) ;
• г) 100111100,1101 (2) ;
• д) 1233,5 (8) ;
• е) 2B3,F4 ( 1 6) .

Вариант 3

• Задание 1
• а) 759 (10) ;
• б) 265 (10) ;
• в) 79,4375 (10) ;
• г) 360,25 (10) ;
• д) 240,25 (10) .
• Задание 2
• а) 1001101 (2) ;
• б) 10001000 ( 2) ;
• в) 100111001,01 (2) ;
• г) 1111010000,001 (2) ;
• д) 1461,15 (8) ;
• е) 9 D,A (16) .

Вариант 4

• Задание 1
• а) 216 (10) ;
• б) 336 (10) ;
• в) 741,125 (10) ;
• г) 712,375 (10) ;
• д) 184,14 (10) .
• Задание 2
• а) 1100000110 (2) ;
• б) 1100010 (2) ;
• в) 1011010,001 (2) ;
• г) 1010100010,001 (2) ;
• д)1537,22 (8) ;
• е) 2 D 9,8 (16) .

Вариант 5

• Задание 1
• а) 530 (10) ;
• б) 265 (10) ;
• в) 597,25 (10) ;
• г) 300,375 (10) ;
• д) 75,57 (10) .
• Задание 2
• а) 101000111 (2) ;
• б) 110001001 (2) ;
• в) 1001101010,01 (2) ;
• г) 1011110100,01 (2) ;
• д) 1317,75 (8) ;
• е) 2F4,0C ( 16 ) .

Вариант 6

• Задание 1
• а) 945 (10) ;
• б) 85 (10) ;
• в) 444,125 (10) ;
• г) 989,375 (10) ;
• д) 237,73 (10) .
• Задание 2
• а) 110001111 (2) ;
• б) 111010001 (2) ;
• в) 100110101,1001 (2) ;
• г) 1000010,01011 (2)
• д) 176,5 (8) ;
• е) 3D2,04 (16) .

Вариант 7

• Задание 1
• а)287 (10) ;
• б) 220 (10) ;
• в) 332,1875 (10) ;
• г) 652,625 (10) ;
• д) 315,21 (10) .
• Задание 2
• а) 10101000 (2) ;
• б) 1101100 (2) ;
• в) 10000010000,01001 (2 ) ;
• г) 1110010100,001 (2) ;
• д) 1714,2 (8) ;
• е) DD,3 (16)

Вариант 8

• Задание 1
• а) 485 (10) ;
• б) 970 (10) ;
• в) 426,375 (10) ;
• г) 725,625 (10) ;
• д) 169,93 (10) .
• Задание 2
• а) 10101000 (2) ;
• б) 101111110 (2) ;
• в) 1010101,101 (2) ;
• г) 1111001110,01 (2) ;
• д) 721,2 (8) ;
• е) ЗС9,8 (16) .

Вариант 9

• Задание 1
• а) 639 (10) ;
• б) 485 (10) ;
• в) 581,25 ( 1 0) ;
• г) 673,5 (10) ;
• д) 296,33 (10)
• Задание 2
• а) 1011000011 (2) ;
• б) 100010111 (2) ;
• в) 1100101101,1 (2) ;
• г) 1000000000,01 (2) ;
• д) 1046,4 (8) ;
• е) 388,64 ( 1 6) .

Вариант 10

• Задание 1
• а) 6181 (10) ;
• б) 556 (10) ;
• в) 129,25 (10) ;
• г) 928,25 (10) ;
• д) 155,45 ( 1 0) .
• Задание 2
• а) 1111011011 (2) ;
• б) 1011101101 (2) ;
• в) 1001110110,011 (2) ;
• г) 1011110011,10111 (2) ;
• д) 675,2 (8) ;
• е) 94,4 (16) .

Вариант 11

• Задание 1
• а) 7721 (10) ;
• б) 71 (10) ;
• в) 284,375 (10) ;
• г) 876,5 (10) ;
• д) 281,86 (10) .
• Задание 2
• а) 1000001111 (2) ;
• б) 10100001 10 (2) ;
• в) 101100110,011011 (2) ;
• г) 100100110,101011 (2) ;
• д) 1022,2 (8) ;
• е) 53,9 ( 1 6) .

Вариант 12

• Задание 1
• а) 233 (10) ;
• б) 243 (10) ;
• в) 830,375 (10) ;
• г) 212,5 (10) ;
• д) 58,89 (10) .
• Задание 2
• а) 1001101111 (2) ;
• б) 1000001110 (2) ;
• в) 111110011,011 (2) ;
• г) 11010101,1001 (2) ;
• д) 1634,5 (8) ;
• е) С2,3 (16) .

Вариант 13

• Задание 1
• а) 218 (10) ;
• б) 767 (10) ;
• в) 894,5 (10) ;
• г) 667,125 ( 1 0) ;
• д) 3,67 (10) .
• Задание 2
• а) 1111100010 (2 ) ;
• б) 1000011110 (2 ) ;
• в) 101100001,011101 ( 2) ;
• г) 1001111001,1 (2) ;
• д) 10 71,54 (8) ;
• е) 18В, 0 С ( 1 6)

Вариант 14

• Задание 1
• а) 898 (10) ;
• б) 751 (10) ;
• в) 327,375 (1 6 ) ;
• г) 256,625 (10) ;
• д) 184,4 (10) .
• Задание 2
• а) 101110100 (2) ;
• б) 1111101101 (2) ;
• в) 1110100001,01 (2 ) ;
• г) 1011111010,0001 (2 ) ;
• д) 744,12 (8 ) ;
• е) 1ЕЕ,С (16) .

Вариант 15

• Задание 1
• а) 557 (10) ;
• б) 730 (10) ;
• в) 494 , 25 (10 ) ;
• г) 737,625 (10) ;
• д) 165,37 (10) .
• Задание 2
• а) 101001101 (2 ) ;
• б) 1110111100 (2 ) ;
• в) 10000001000,001 (2 ) ;
• г) 1000110110,11011 (2 ) ;
• д) 147,56 (8) ;
• е) 1СА,3 ( 1 6) .

Вариант 16

• Задание 1
• а) 737 (10) ;
• б) 92 (10) ;
• в) 934,25 (10) ;
• г) 413,5625 (10) ;
• д) 100,94 (10) .
• Задание 2
• а) 1110000010 (2) ;
• б) 1000100 (2) ;
• в) 110000100,001 (2) ;
• г) 1001011111,00011 (2) ;
• д) 665,42 (8) ;
• е) 24б,18 (16) .

Вариант 17

• Задание 1
• а) 575 ( 1 0) ;
• б) 748 ( 1 0) ;
• в) 933,5 ( 1 0 ) ;
• г) 1005,375 (10) ;
• д) 270,44 (1 0 ) .
• Задание 2
• а) 1010000 (2 ) ;
• б) 10010000 (2) ;
• в) 1111010000,01 (2 ) ;
• г) 101000011,01 (2 ) ;
• д) 1004,1 (8 ) ;
• е) 103,8C (16) .

Вариант 18

• Задание 1
• а) 563 (10) ;
• б) 130 (10) ;
• в) 892,5 ( 1 0) ;
• г) 619,25 (10 ) ;
• д) 198,05 (10) .
• Задание 2
• а) 11100001 (2 ) ;
• б) 101110111 (2 ) ;
• в) 1011110010,0001 (2) ;
• г) 1100010101,010101 (2) ;
• д) 533,2 (8) ;
• е) 32,22 ( 1 6) .

Вариант 19

• Задание 1
• а) 453 ( 1 0 ) ;
• б) 48 1 (1 0) ;
• в) 461,25 ( 1 0) ;
• г) 667,25 (10 ) ;
• д) 305,88 (10) .
• Задание 2
• а) 111001010 (2 ) ;
• б) 1101110001 (2 ) ;
• в) 1001010100,10001 (2) ;
• г) 111111110,11001 (2 ) ;
• д)1634,35 (8) ;
• е) 6В,А (16) .

Вариант 20

• Задание 1
• а) 572 (10) ;
• б) 336 (10) ;
• в) 68,5 (10) ;
• г) 339,25 (10) ;
• д) 160,57 (10) .
• Задание 2
• а) 1010110011 (2) ;
• б) 1101110100 (2) ;
• в) 1010101,101 (2) ;
• г) 1101000,001 (2) ;
• д) 414,1 (8) ;
• е) 366,4 (16) .

Вариант 21

• Задание 1
• а) 949 (10) ;
• б) 763 (10) ;
• в) 994,125 (10) ;
• г) 523,25 (10) ;
• д) 203,82 (10) .
• Задание 2
• а) 1110001111 (2) ;
• б) 100011011 (2) ;
• в) 1001100101,1001 (2) ;
• г) 1001001,011 (2) ;
• д) 335,7 (8) ;
• е) 14С,А (16) .

Вариант 22

• Задание 1
• а) 563 (10) ;
• б) 264 (10) ;
• в) 234,25 (10) ;
• г) 53,125 (10) ;
• д) 286,16 (10) .
• Задание 2
• а) 1100010010 (2) ;
• б) 10011011 (2) ;
• в) 1111000001,01 (2) ;
• г) 10110111,01 (2) ;
• д) 416,1 (8) ;
• е) 215,7 (16) .

Вариант 23

• Задание 1
• а) 279 (10) ;
• б) 281 (10) ;
• в)841,375 (10) ;
• г)800,3125 (10) ;
• д)208,92 (10) .
• Задание 2
• а) 1100111001 (2) ;
• б) 10011101 (2) ;
• в) 1111011,001 (2) ;
• г) 110000101,01 (2) ;
• д) 1601,56 (8) ;
• е) 16Е,В4 (16) .

Вариант 24

• Задание 1
• а) 744 (10) ;
• б) 554 (10) ;
• в) 269,375 (10) ;
• г) 120,25 (10) ;
• д) 139,09 (10) .
• Задание 2
• а) 101000001 (2) ;
• б) 1110111100 (2) ;
• в) 1001110101,011001 (2) ;
• г) 1000010001,00011 (2) ;
• д) 1177,6 (8) ;
• е) 3FA,E8 ( 1 6) .

Вариант 25

• Задание 1
• а) 686 (10) ;
• б) 585 (10) ;
• в) 530,6875 (10) ;
• г)87,375 (10) ;
• д)131,82 (10) .
• Задание 2
• а) 110111001 (2) ;
• б) 101111011 (2) ;
• в) 1110111100,1 (2) ;
• г) 110000011,0111 (2) ;
• д) 742,34 (8) ;
• е) 396,А (16) .

• Для выполнения арифметических операций в двоичной системе счисления необходимо иметь соответствующие таблицы сложения и умножения.

• Для выполнения арифметических операций в восьмеричной системе счисления необходимо иметь соответствующие таблицы сложения и умножения.

• Для выполнения арифметических операций в шестнадцатеричной системе счисления необходимо иметь соответствующие таблицы сложения и умножения.

• Пример 1. Сложить числа:
• а) 10000000100 (2) + 111000010 (2) = 10111000110 (2) ;
• б)223,2 (8) + 427,54 (8) = 652,74 (8) ;
• в)ЗВЗ,6 (16) +38В,4 (16) =73Е,А (16) .

• Пример 2. Выполнить вычитание:
• а)1100000011,011 (2) - 101010111,1 (2) = 110101011,111 (2) ;
• б)1510,2 (8) - 1230,54 (8) = 257,44 (8) ;
• в) 27D,D8 ( 1 6) - 191,2 (16) = ЕС,В8 (16) .

• Пример 3 . Выполнить умножение:
• а) 100111 (2) х 1000111 (2) = 101011010001 (2) ;
• б) 1170,64 (8) х46,3 (8) = 57334,134 (8) ;
• в) 61,А (16) х40, D (16) = 18В7,52 ( 1 6) .

Задания к практической работе

• 1. Сложите числа.
• 2. Выполните вычитание.
• 3. Выполните умножение.
• Примечание. В заданиях 1 - 3 проверьте правильность вычислений переводом исходных данных и результатов в десятичную систему счисления. В задании 1 д) получите пять знаков после запятой в двоичном представлении.

Вариант 1

• Задание 1
• а)1101100000 (2) + 10110110 (2) ;
• б) 101110111 (2) + 1000100001 (2) ;
• в)1001000111,01 (2) + 100001101,101 (2) ;
• г) 271,34 (8) + 1566,2 (8) ;
• д) 65,2 (16) + ЗСА,8 (16) .
• Задание 2
• а)1011001001 (2) - 1000111011 (2) ;
• б) 1110000110 (2) - 101111101 (2) ;
• в)101010000,10111 (2) - 11001100,01 (2) ;
• г) 731,6 (8) - 622,6 (8) ;
• д) 22 D ,1 (16) - 123,8 (16) .
• Задание 3
• а) 1011001 (2) *1011011 (2) ;
• б) 723,1 (8) *50,2 (8) ;
• в) 69,4 (16) *А,В (16) .

Вариант 2

• Задание 1
• а) 1010101 (2) + 10000101 (2) ;
• б) 1111011101 (2) + 101101000 (2 ) ;
• в) 100100111,001 (2) + 100111010,01 (2) ;
• г) 607,54 (8) + 1620,2 (8) ;
• д) 3BF,A ( 1 6 ) + 313,А (16) .
• Задание 2
• а) 1001000011 (2) – 10110111 (2) ;
• б) 111011100 (2) - 10010100 (2) ;
• в) 1100110110,0011 (2) - 11111110,01 (2) ;
• г) 1360,14 (8) - 1216,4 (8) ;
• д) ЗЗВ,6 (16) - 11В,4( 16) .
• Задание 3
• а) 11001 (2) *1011100 (2) ;
• б) 451,2 (8) *5,24 (8) ;
• в) 2В,А (16) *36,6 (16) .

Вариант 3

• Задание 1
• а) 100101011 (2) + 111010011 (2) ;
• б) 1001101110 (2) + 1101100111 (2) ;
• в) 1010000100,1 (2) + 11011110,001 (2) ;
• г) 674,34 (8) + 1205,2 (8) ;
• д) 2 FE ,6 ( 1 6) + ЗВ,4 (16) .
• Задание 2
• а) 1100110010 (2) – 1001101101 (2) ;
• б) 1110001100 (2) – 10001111 (2) ;
• в) 11001010,01 (2) - 1110001,001 (2) ;
• г) 641,6 (8) - 273,04 (8) ;
• д) ЗСЕ,В8 (16) - 39А,В8 (16) .
• Задание 3
• а) 1010101 (2) *1011001 (2) ;
• б) 1702,2 (8) *64,2 (8) ;
• в)7,4 (16) * 1 D ,4 (16) .

Вариант 4

• Задание 1
• а) 101111111 (2) + 1101110011 (2) ;
• б) 10111110 (2) + 100011100 (2) ;
• в) 1101100011,0111 (2) + 1100011,01 (2)
• г) 666,2 (8) + 1234,24 (8) ;
• д) 346,4 (16) ; + 3F2, 6 (16) .
• Задание 2
• а) 1010101101 (2) - 110011110 (2) ;
• б) 1010001111 (2) - 1001001110 (2) ;
• в) 11111000100,11011 (2) - 101110111,011 (2) ;
• г) 1437,24 (8) - 473,4 (8) ;
• д) 24А,4 (16) - В3,8 (16) .
• Задание 3
• а) 101011 (2) * 1001 11 (2) ;
• б) 1732,4 (8) * 34,5 (8) ;
• в) 36,4 (16) * А,А (16) .

Вариант 5

• Задание 1
• а) 1100011010 ( 2 ) + 11101100 (2) ;
• б) 10111010 (2) + 1010110100 (2) ;
• в) 1000 1 10111,011 (2) + 1110001111,001 (2) ;
• г) 1745,5 (8) + 1473,2 (8) ;
• д) 24D,5 (16) + 141,4 (16) .
• Задание 2
• а) 1100101010 (2) – 110110010 (2) ;
• б) 110110100 (2) - 110010100 (2) ;
• в) 1101111111,1 (2) -1100111110,1011 (2) ;
• г) 1431,26 (8) - 1040,3 (8) ;
• д) 22С,6 (16) - 54,2 (16) .
• Задание 3
• а) 1001001 (2) *11001 (2)
• б) 245,04 (8) * 112,2 (8) ;
• в) 4В,2 (16) * ЗС,3 (16)

Вариант 6

• Задание 1
• а) 1000011101 (2) + 101000010 (2) ;
• б) 100000001 (2) + 1000101001 (2) ;
• в) 101111011,01 (2) + 1000100,101 (2) ;
• г) 1532,14 (8) + 730,16 (8) ;
• д) BB,4 ( 16) + 2F0,6 (16) .
• Задание 3
• а) 1000101110 (2) – 1111111 (2) ;
• б) 1011101000 (2) - 1001000000 (2) ;
• в) 1000101001,1 (2) – 1111101,1 (2) ;
• г) 1265,2 (8) - 610,2 (8) ;
• д) 409,D (16) - 270,4 (16) .
• Задание 3
• а) 111010 (2) * 1100000 (2) ;
• б) 1005,5 (8) * 63,3 (8) ;
• в) 4A,3 (16) * F,6 (16) .

Вариант 7

• Задание 1
• а) 1100110 (2) + 1011000110 (2) ;
• б) 1000110 (2) + 1001101111 0 (2) ;
• в) 101001100,101 (2) + 1001001100,01 (2) ;
• г) 275,2 (8) + 724,2 (8) ;
• д) 165,6 (16) + ЗЕ,В (16) .
• Задание 2
• а) 1011111111 (2) – 100000011 (2) ;
• б) 1110001110 (2) -100001011 (2) ;
• в) 110010100,01 (2) - 1001110,1011 (2) ;
• г) 1330,2 (8) - 1112,2 (8) ;
• д) АВ,2 (16) - ЗЕ,2 (16) .
• Задание 3
• а)110000 (2) * 1101100 (2) ;
• б) 1560,2 (8) * 101,2 (8 ) ;
• в) 6,3 (16) * 53, A (1 6) .

Вариант 8

• Задание 1
• а) 1010100111 (2) + 11000000 (2) ;
• б) 1110010010 (2) + 110010111 (2) ;
• в) 1111111,101 (2) + 101010101,101 (2) ;
• г) 1213,44 (8) + 166,64 (8) ;
• д) 41,4 ( 16) + 3CF,D (16) .
• Задание 2
• а) 1010000000 (2) - 1000101010 (2) ;
• б) 1011010101 (2) - 110011001 (2) ;
• в) 1001001010,11011 (2) - 1000111000,01 (2) ;
• г) 1145,2 (8) - 1077,5 (8) ;
• д) 380,1 (16) - 2 DC ,3 (16) .
• Задание 3
• а) 111011 (2 ) * 100000 (2) ;
• б) 511,2 (8) * 132,4 (8) ;
• в) 68,4 (16) * 37,8 ( 1 6) .

Вариант 9

• Задание 1
• а) 1000010100 (2) + 1101010101 (2) ;
• б) 1011001010 (2 ) + 101011010 (2) ;
• в) 1110111000,101 (2) + 1101100011,101 (2) ;
• г) 1430,2 (8) + 666,3 (8) ;
• д) 388,3 ( 1 6) + 209,4 (16) .
• Задание 2
• а) 1111100010 (2) - 101011101 (2) ;
• б) 1011000100 (2) - 1000100000 (2) ;
• в) 1101111000,1001 (2) - 1000000,01 (2) ;
• г) 1040,2 (8) - 533,2 (8) ;
• д) 3FB,4 (16) - 140,6 (16) .
• Задание 3
• а) 11111 (2) * 10001 (2) ;
• б) 1237,3 (8) * 117,5 (8) ;
• в) 66,4 (16) *65,8 ( 1 6) .

Вариант 10

• Задание 1
• а) 11111010 (2) + 10000001011 (2) ;
• б) 1011010 (2) + 1001111001 (2) ;
• в) 10110110,01 (2) + 1001001011,01 (2) ;
• г) 1706,34 (8) + 650,3 (8) ;
• д) 180,4 (16) + 3А6,28 (16) .
• Задание 2
• а) 111101101 (2) - 101111010 (2) ;
• б) 10001 10100 (2) – 100100111 (2) ;
• в) 1111111011,01 (2) - 100000100,011 (2) ;
• г) 1300,44 (8) - 1045,34 (8) ;
• д) 16А,8 (16) - 147,6 ( 1 6) .
• Задание 3
• а) 100111 (2) * 110101 (2) ;
• б) 1542,2 (8) * 50,6 (8) ;
• в) А,8 ( 1 6) * Е,2 (16) .

Вариант 11

• Задание 1
• а) 1100111 (2) + 1010111000 (2) ;
• б) 1101111010 (2) + 1000111100 (2) ;
• в) 1111101110,01 (2) + 1110001,011 (2) ;
• г) 153,3 (8) + 1347,2 (8) ;
• д) Е0,2 (16) + 1Е 0 ,4 (16) .
• Задание 2
• а) 1010101110 (2) - 11101001 (2) ;
• б) 1000100010 (2) - 110101110 (2) ;
• в) 1010100011,011 (2) - 1000001010,0001 (2) ;
• г) 1517,64 (8) - 1500,3 (8) ;
• д) 367,6 (16) - 4А,С ( 1 6) .
• Задание 3
• а) 1100110 (2) * 101111 (2) ;
• б) 1272,3 (8) * 23,14 (8) ;
• в) 48,4 (16) * 5,А (16) .

Вариант 12

• Задание 1
• а) 1101111001 (2) + 1010010101 (2) ;
• б) 1111001001 (2) + 10 01100100 (2) ;
• в) 100110010,011 (2) + 110001000,011 (2) ;
• г) 1712,14 (8) + 710,4 (8) ;
• д) Е6,1 (16) + 38С,8 (16) .
• Задание 2
• а) 1000001110 (2) - 100100001 (2) ;
• б) 1101000110 (2) - 1001101000 (2) ;
• в) 1011001111,01 (2) - 110100010,01 (2) ;
• г) 1734,4 (8) - 134,2 (8) ;
• д) 2 F 2, A (1 6 ) - 22 D , A (16) .
• Задание 3
• а) 1000000 (2) * 100101 (2) ;
• б) 103 , 2 ( 8) * 147,04 (8) ;
• в) 67,4 (16) * 54,8 (16 ) .

Вариант 13

• Задание 1
• а) 1000011111 (2) + 1111100 (2 ) ;
• б) 1011100011 (2) + 111110110 (2) ;
• в) 111111100,1 (2) + 1011100100,1 (2) ;
• г) 1777,2 (8) + 444,1 (8) ;
• д) 3 EF ,3 (16) + С7,4 (16) .
• Задание 2
• а) 1101000100 (2) - 101010101 (2) ;
• б) 1110010111 (2) - 1011100 (2) ;
• в) 1100101111,01 (2) - 10010001,01 (2) ;
• г) 640,2 (8) - 150,22 (8) ;
• д) 380,68 (16) - 50,4 (16) .
• Задание 3
• а) 100010 (2) *1100110 (2) ;
• б) 741,4 (8) * 141,64 (8) ;
• в) B ,7 (16) *D , C (16) .

Вариант 14

• Задание 1
• а) 1001000000 (2 ) + 101010110 (2) ;
• б) 11000010 (2) + 1001110100 (2) ;
• в) 1011101110,1 (2) + 11 100101,01 (2) ;
• г) 2015,1 (8) + 727,54 (8) ;
• д) 9 D ,8 (16) + ED ,8 (16) .
• Задание 2
• а) 1010000100 (2) - 1000001000 (2) ;
• б) 1111110011 (2) - 1001101001 (2) ;
• в) 101001100,101 (2) - 100100101,1 (2) ;
• г) 1024,6 (8) - 375,14 (8) ;
• д) ЗЕ9,4 ( 1 6) - 72,6 (16) .
• Задание 3
• а) 1001010 (2) * 1001000 (2 ) ;
• б) 747,2 (8) * 64,14 (8) ;
• в) 56,1 (16) * 33,С (16) .

Вариант 15

• Задание 1
• а) 1101100001 (2 ) + 1001101110 (2) ;
• б) 1101010101 (2) + 101011001 (2) ;
• в) 1101111110,011 (2 ) + 1100101101,1011 (2 ) ;
• г) 1771,2 (8 ) + 300,5 (8) ;
• д) 2F2,8 (16) + Е4,В (16) .
• Задание 2
• а) 1111000000 (2) - 111101000 (2) ;
• б) 1100110111 (2) - 1001110000 (2 ) ;
• в) 1000011110,1001 (2 ) - 110000111,01 (2) ;
• г) 1436,34 (8) - 145,2 (8) ;
• д) 3F5,98 (16) - 240,3 (16) .
• Задание 3
• а) 1011100 (2 ) * 101000 (2 ) ;
• б) 1300,6 (8) * 65,2 (8 )
• в)68,А ( 1 6 ) * 9,6 ( 1 6 ) .

Вариант 16

• Задание 1
• а)11110100 (2) + 110100001 (2) ;
• б) 1101110 (2) + 101001000 (2) ;
• в) 1100110011,1 (2) + 1 11 000011,101 (2) ;
• г) 1455,04 (8) + 203,3 (8) ;
• д) 14Е,8 ( 1 6) + 184,3 (16) .
• Задание 2
• а) 1000010101 (2) - 100101000 (2) ;
• б) 1001011011 (2) - 101001110 (2) ;
• в) 111111011,101 (2) - 100000010,01 (2) ;
• г) 341,2 (8) - 275,2 (8) ;
• д) 249,5 (16) - ЕЕ, A (16) .
• Задание 3
• а) 1001000 (2) *1010011 (2) ;
• б)412,5 (8) *13,1 (8) ;
• в)3В, A (16) *10,4 ( 16) .

Вариант 17

• Задание 1
• а) 1011110101 (2 ) + 1010100110 (2 ) ;
• б) 1001100011 (2) + 1110010010 (2 ) ;
• в) 1111110100,01 (2) + 110100100,01 (2 ) ;
• г) 755,36 (8 ) + 1246,5 (8) ;
• д) 8D,2 (16) + 63,8 ( 1 6) .
• Задание 2
• а) 1100111110 (2) - 1 10 1001 (2) ;
• б) 1101111011 (2) - 1101110101 (2) ;
• в) 1101001010,011 (2 ) - 1010011110,101 (2 ) ;
• г) 1632,1 (8) - 706,34 (8) ;
• д) 283,С (16 ) - 19С,8 ( 1 6) .
• Задание 3
• а) 111000 (2 ) * 1101001 (2 ) ;
• б) 133,6 (8) * 73,4 (8) ;
• в) 46,8 (16) * В,А (16) .

Вариант 18

• Задание 1
• а) 1100100011 (2 ) + 1101001111 ( 2) ;
• б) 111101111 (2 ) + 10 010100 (2 ) ;
• в) 1010010000,0111 ( 2 ) + 111010100,001 (2 ) ;
• г) 1724,6 (8) + 1322,2 (8 ) ;
• д) 2С7,68 ( 1 6 ) + 6 F ,4 ( 1 6) .
• Задание 2
• а) 111001110 (2 ) - 11011011 (2 ) ;
• б) 1011000001 (2) - 110100001 (2) ;
• в) 1011111101,1 (2) - 111100000,01 (2) ;
• г) 1126,06 (8) - 203,54 (8) ;
• д) 32 B , D (16) - 187, D 8 (16) .
• Задание 3
• а)1100101 (2) *1001010 (2) ;
• б)1544, 4 (8) * 16,64 ( 8) ;
• в) 69,8 ( 1 6) * 30,8 (1 6 )

Вариант 19

• Задание 1
• а) 101110001 (2) + 101111001 (2) ;
• б) 1110001110 (2) + 1100110111 (2) ;
• в) 10000011010,01 (2) + 1010010110,01 (2) ;
• г) 1710,2 (8) + 773,24 (8) ;
• д) 3Е7,7 (16) + 32,2 (16) .
• Задание 2
• а) 1111000010 (2) - 1110000011 (2) ;
• б) 1110101011 (2) – 111000111 (2) ;
• в) 1111011010,011 (2) - 1011100111,01 (2) ;
• г) 1650,2 (8) - 502,2 (8) ;
• д) ЗЕ0,6, (16) - 17Е,9 (16) .
• Задание 3
• а) 1001101 (2) *11111 (2) ;
• б) 1226,1 (8) *24,4 (8) ;
• в) 36,6 ( 16) *38 ,4 ( 1 6) .

Вариант 20

• Задание 1
• а) 10001000 (2) + 1011010010 (2) ;
• б) 111110011 (2) + 111110000 (2) ;
• в) 1010001010,1011 (2) + 1101010100,011 (2) ;
• г) 711,2 (8) + 214,2 (8) ;
• д) 7А,58 (16) + 2 D 0,9 (16) .
• Задание 2
• а) 110111010 (2) - 1110001 (2) ;
• б) 1100001000 (2) - 11000100 (2) ;
• в) 1111111010,01 (2) - 1000110010,0101 (2) ;
• г) 1060,52 (8) - 761,14 (8) ;
• д) 1С0,6 (16) - 8 D ,2 (16) .
• Задание 3
• а) 11101 (2) *110101 (2) ;
• б)1106,2 (8) *145,2 (8) ;
• в) 65,4 (16) *55,9 (16) .

Вариант 21

• Задание 1
• а) 1110101010 (2) + 10111001 (2) ;
• б) 10111010 (2) + 10010100 (2) ;
• в) 111101110,1011 (2) + 1111011110,1 (2) ;
• г) 1153,2 (8) + 1147,32 (8) ;
• д) 40F,4 (16) + 160,4 (16) .
• Задание 2
• а) 1000000100 (2) - 101010001 (2) ;
• б) 1010111101 (2) - 111000010 (2) ;
• в) 1101000000,01 (2) - 1001011010,011 (2) ;
• г) 2023,5 (8) - 527,4 (8) ;
• д) 25Е,6 (16) - 1В1,5 (16) .
• Задание 3
• а) 1001011 (2) *1010110 (2) ;
• б) 1650,2 (8) *120,2 (8) ;
• в) 19,4 (1 6) * 2F,8 (1 6) .

Вариант 22

• Задание 1
• а) 10111111 (2) + 1100100001 (2) ;
• б) 110010100 (2) + 1011100001 (2) ;
• в) 10000001001,0101 (2) + 1010000110,01 (2) ;
• г) 1512,4 (8) + 1015,2 (8) ;
• д) 274,5 (16) + DD ,4 (16) .
• Задание 2
• а) 1000001001 (2) - 111110100 (2) ;
• б) 1111000101 (2) – 1100110101 (2) ;
• в) 1100110101,1 (2) - 1011100011,01 (2) ;
• г) 1501,34 (8) - 1374,5 (8) ;
• д) 12 D ,3 (16) - 39,6 (16) .
• Задание 3
• а) 111101 (2) *10 l 0111 (2) ;
• б) 1252,14 (8) *76,04 (8) ;
• в) 66,68 (16) *1Е,3 (16) .

Вариант 23

• Задание 1
• а) 1000100001 (2) + 1011100110 (2) ;
• б) 1101110011 (2) + 111000101 (2) ;
• в) 1011011,01 (2) + 1000101110,1001 (2) ;
• г) 665,1 (8) + 1217,2 (8) ;
• д) 30С,7 (16) + 2А1,8 (16) .
• Задание 2
• а) 11110010 (2) - 10101001 (2) ;
• б) 1110100001 (2) - 1011001001 (2) ;
• в) 1101001010,1 (2) - 1011101001,11011 (2) ;
• г) 166,14 (8) - 143,2 (8) ;
• д) 287,А (16) - 62,8 (16) .
• Задание 3
• а) 1001001 (2) *100010 (2) ;
• б) 324,2 (8) *122,12 (8) ;
• в) F,4 ( 1 6) * 38,6 ( 1 6) .

Вариант 24

• Задание 1
• а) 10000001010 (2) + 11111111 (2) ;
• б) 111011000 (2) + 1110111 (2) ;
• в) 111010101,101 (2) + 11101111,001 (2) ;
• г) 251,42 (8) + 72,54 (8) ;
• д) 2CF,A ( 1 6 ) + 242,4 ( 1 6) .
• Задание 2
• а) 1001000100 (2) - 100111010 (2) ;
• б) 100001100 (2) - 10110011 (2) ;
• в) 1110111100,011 (2) - 1100000011,0111 (2) ;
• г) 1700,2 (8) - 456,44 (8) ; д) 1А1,8 (16) - Е0,7 (16) .
• Задание 3
• а) 11110 (2) *1100100 (2) ;
• б) 1034,6 (8) *43,1 (8) ;
• в) 2C,4 ( 1 6) * 6,2 ( 16) .

Вариант 25

• Задание 1
• а) 10000010001 (2) + 1000100010 (2) ;
• б) 101011100 (2) + 10101111 (2) ;
• в) 1001110000,001 (2) + 10100101,011 (2) ;
• г) 121б,2 (8) + 2012,4 (8) ;
• д) 372,18 (16) + 251,38 (16) .
• Задание 2
• а) 100110110 (2) - 11101001 (2) ;
• б) 1010100111 (2) - 110000010 (2) ;
• в) 11001101,1011 (2) - 1001101,011 (2) ;
• г) 1254,2 (8) - 1150,54 (8) ;
• д) 2Е1,8 (16) - 19А,4 (16) .
• Задание 3
• а) 1101000 (2) *10011 (2) ;
• б)1411,44 (8) *46,4 (8) ;
• в) 63,8 (16) *8,6 (16) .

• Перевод чисел из одной системы счисления в другую
• Поскольку в практической деятельности люди привыкли оперировать десятичной системой счисления, а в ЭВМ числа представляются в двоичной, необходимо научиться преобразовывать числа из одной системы счисления в другую. Рассмотренные выше правила перевода из двоичной системы счисления в восьмеричную и шестнадцатеричную и наоборот носят частный характер и не могут быть распространены на другие системы. Здесь же мы рассмотрим общие правила перевода, справедливые для любой пары систем счисления, хотя и более громоздкие и трудоемкие по сравнению с рассмотренными выше.
• Правила перевода целых и дробных чисел не совпадают, поэтому приведем три правила перевода чисел из системы счисления с основанием R в систему счисления с основанием Q.

• Правило 1. Перевод целых чисел
• Для перевода целого числа N, представленного в системе счисления (с/с) с основанием R, в с/с с основанием Q необходимо данное число делить на основание Q по правилам с/с с основанием R до получения целого остатка, меньшего Q. Полученное частное снова необходимо делить на основание Q до получения нового целого остатка, меньшего Q, и т.д., до тех пор, пока последнее частное будет меньше Q. Число N в с/с с основанием Q представится в виде не упорядоченной последовательности остатков деления в порядке, обратном их получению (иными словами, старшую цифру числа N дает последнее частное).

• Пример. Преобразовать десятичное число 67 в двоичную форму.
• Основание исходной системы счисления R=10. Основание новой системы счисления Q=2.
• Согласно приведенному правилу надо исходное число 67 делить на основание новой системы (на 2) по правилам десятичной системы счисления (исходная с/с).
• Поскольку процесс деления на 2 очень прост, воспользуемся следующим приемом: в левом столбце будем писать текущие частные, а в правом - текущие остатки от их деления на 2 (это может быть либо 0, либо 1):
• 67 1 При делении 67 на 2 получается частное 33 и остаток 1;
• 33 1 при делении 33 - частное 16 и остаток 1 и т.д.
• 16 0
• 8 0
• 4 0
• 2 0
• 1 1
• Теперь можно записать число 67 в новой системе счисления. Оно равно 1000011.

• Правило 2. Перевод правильной дроби
• Перевод правильной дроби, представленной в с/с с основанием R, в с/с с основанием Q заключается в последовательном умножении этой дроби на основание Q по правилам системы счисления с основанием R, причем перемножают только дробные части. Дробь N в с/с с основанием Q представляется в виде упорядоченной последовательности целых частей произведений в порядке их получения. (Иными словами, старший разряд является первой цифрой произведения). Количество последовательных произведений определяет количество цифр в полученном числе.
• Для многих чисел указанный процесс умножения потенциально никогда не кончается. Поэтому он продолжается до тех пор, пока не будет получено необходимое число цифр дробной части. При переводе числа с целью представления ее в “машинной” форме можно точно указать требуемое количество цифр.

старшая цифра 0,4486 * 2 = 0,8972 0 0,8942 * 2 = 1,7944 1 0,7944 * 2 = 1,5888 1 0,5888 * 2 = 1,1776 1 0,1776 * 2 = 0,3552 0 0,3552 * 2 = 0,7104 0 Искомое представление число 0,7243 в двоичной системе счисления - 0,101110." width="640"

• Пример. Перевести в двоичную систему счисления десятичную дробь 0,7243.
• Основание исходной системы счисления R=10. Основание новой системы счисления Q=2.
• Согласно приведенного правила исходное число 0,7243 надо умножать на основание новой системы (на 2) по правилам десятичной системы счисления (исходная с/с). Выполним серию умножений до получения, например, шести цифр в двоичном числе:
• Искомые цифры дроби:
• 0,7243 * 2 = 1,4486 1 - старшая цифра
• 0,4486 * 2 = 0,8972 0
• 0,8942 * 2 = 1,7944 1
• 0,7944 * 2 = 1,5888 1
• 0,5888 * 2 = 1,1776 1
• 0,1776 * 2 = 0,3552 0
• 0,3552 * 2 = 0,7104 0
• Искомое представление число 0,7243 в двоичной системе счисления - 0,101110.

• Обратите внимание, что для получения шести цифр дроби выполнено семь умножений
• Это связано с необходимостью выполнить округление, чтобы представить дробь заданной длины более точно.
• Из последнего примера, конечная дробь в одной системе счисления может стать бесконечной в другой. Это утверждение справедливо для всех случаев, когда одна система счисления не может быть получена возведением в целую степень основания другой.
• Примеры.
• Десятичная дробь 0,2 представляется бесконечной дробью 0,33333... в шестнадцатеричной системе счисления (основания с/с 10 и 16).
• Шестнадцатеричная дробь 0,В1 представляется конечной дробью 0,10110001 в двоичной системе счисления (основания с/с 16 и 2).
• Правило 3. Перевод неправильной дроби
• Перевод неправильной дроби из одной системы счисления в другую осуществляется отдельно для целой и дробной части по правилам, изложенным выше

• Перевести число 10110,000111011 в восьмеричную систему счисления.
• Перевести число 10110,000111011 в шестнадцатеричную систему счисления.
• Перевести число 34 AD 3,01916, в двоичную систему счисления
• Перевести числа 101010,11101; 100010,011101; 1111000000,101 - в восьмеричную систему счисления
• Перевести числа 101111,01100; 100000111,001110; 101010,0010 - в шестнадцатеричную систему счисления
• Переведите восьмеричные числа в двоичную систему счисления:
• А) 276; 0,635; 25,024 Б) 265; 0,111; 201,302
• Переведите шестнадцатеричные числа в двоичную систему счисления: А) 1АС7; 0,ЗС1; F 4 A , CC Б ) CCAF; 0,AAA; DDBB,A
• Переведите числа из шестнадцатеричной системы счисления в восьмеричную: А) А54; 21 E ,7 F ; 0, FD Б )C25,F9; 1 2A; 0,ABCD Б) 344; 0,7612; 333,222
• Переведите числа из восьмеричной системы счисления в шестнадцатеричную: 777; 0,1234; 654,765

• Как уже говорилось выше, кодом называют такую запись числа, которая отличается от естественной и общепринятой. Так вот, в математике естественной формой записи числа является запись, при которой непосредственно перед старшей значащей цифрой числа помещается знак плюс(+) или минус(-), а длина записи определяется величиной числа (иначе, количество символов, использованных для записи разных чисел, как правило, не совпадает). В ЭВМ это не так. Одной из важнейших характеристик любой ЭВМ является длина слова в ней. Длина слова определяется количеством двоичных разрядов слова.
• Поэтому в ЭВМ, вне зависимости от величины числа, его код всегда имеет фиксированное количество двоичных цифр.
• Кроме этого, в двоичном алфавите нет никаких символов, кроме цифр 0 и 1, и необходимы новые правила для указания знака числа. Суть этих правил сводится к тому, что знак плюс изображается цифрой 0, знак минус - цифрой 1, а цифра, изображающая знак всегда записывается самой первой в записи числа.

• Обратите внимание, что код числа всегда содержит изображение его знака, в отличие от математической записи, которая позволяет опускать знак плюс при изображении положительного числа.
• Так, код 011101, согласно этим правилам, изображает положительное (самая левая цифра - 0) двоичное число 11101.
• Для того, чтобы более просто, и, следовательно, более экономично реализовать устройство АЛУ применяют несколько разных кодов чисел. Это связано с тем, что разные операции в ЭВМ более просто реализуются в разных кодах.
• При выполнении арифметических операций в ЭВМ применяют прямой, обратный и дополнительный коды чисел.

• Прямой код двоичного числа - это само двоичное число, в котором все цифры, изображающие его значение, записываются как в математической записи, а знак числа записывается двоичной цифрой.
• При этом никакого символа, отделяющего эту цифру от старшей цифры, используемой при изображении его величины, не допускается. В таких случаях говорят о том, что назначение цифры в коде определяется его позицией.
• Примеры.
• Изображаемое число Код
• +1101 (+13) 0000 1101 ( В примерах коды )
• +1011101 (+93) 0101 1101 ( изображаются )
• 1101 (-13) 1000 1101 ( восемью цифрами )
• Итак, прямой код почти не отличается от принятого в математике: для выявления абсолютной величины (модуля) числа, надо отбросить цифру, обозначающую его знак.

• Однако применительно к операциям сложения и вычитания такой код неудобен: правила счета для положительных и отрицательных чисел различаются. Чтобы прояснить это обстоятельство, представим что длина кода (слова) равна 5 двоичным разрядам и запишем несколько чисел в нем:
• Как видно из примера, при использовании прямого кода при переходе значения число через ноль, происходит скачкообразное изменение кода! Поэтому построение устройства, в котором должны выполняться такие действия арифметики, как сложение чисел с разными знаками и вычитание, становится сложной задачей.
• Прямой код используется при хранении чисел в памяти ЭВМ, а также при выполнении операций умножения и деления.

• Чтобы построить более простые схемы АЛУ предложены и активно применяются обратный и дополнительный коды.
• Обратный код положительного числа совпадает с прямым, а при записи отрицательного числа все его цифры, кроме цифры, изображающей знак числа, заменяются на противоположные (0 заменяется на 1, а 1 - на 0).
• Примеры записи.
• Изображаемое число Код
• +1101 (+13) 0000 1101 ( В примерах коды )
• +1011101 (+93) 0101 1101 ( изображаются )
• 1101 (-13) 1111 0010 ( восемью цифрами )
• Сопоставление этой записи с прямым кодом показывает, что непосредственно восстановить абсолютную величину (модуль) отрицательного числа непросто. Однако, в этом коде как к положительным, так и к отрицательным числам можно применять одни и те же правила, а операцию А-В можно заменить операцией сложения чисел А и “минус В”.

• При этом никакого символа, отделяющего эту цифру от старшей цифры, используемой при изображении его величины, не допускается. В таких случаях говорят о том, что назначение цифры в коде определяется его позицией.
• Примеры.
• Изображаемое число Код
• +1101 (+13) 0000 1101 ( В примерах коды )
• +1011101 (+93) 0101 1101 ( изображаются )
• 1101 (-13) 1000 1101 ( восемью цифрами )
• Итак, прямой код почти не отличается от принятого в математике: для выявления абсолютной величины (модуля) числа, надо отбросить цифру, обозначающую его знак.
• Однако применительно к операциям сложения и вычитания такой код неудобен: правила счета для положительных и отрицательных чисел различаются. Чтобы прояснить это обстоятельство, представим что длина кода (слова) равна 5 двоичным разрядам и запишем несколько чисел в нем:

• Посмотрим, как представляется последовательные числа при переходе через ноль:
• Из примера видно, что переход через ноль также не выглядит естественным. Отмеченная особенность влечет за собой и следующее - в обратном коде ноль изображают две различающиеся комбинации: 00000 (+0) и 11111 (-0), что усложняет аппаратную реализацию операций.
• Для восстановления прямого кода отрицательного числа из обратного кода надо все цифры, кроме цифры, изображающей знак числа, заменить на противоположные.

- 101101 Прямой код - 1101101 Обратный код - 1010010 +1 Дополнительный - 1010011" width="640"

• Дополнительный код положительного числа совпадает с прямым, а код отрицательного числа образуется как результат увеличения на 1 его обратного кода.
• Иными словами, процесс построения дополнительного кода отрицательного числа можно разбить на два этапа - построить обратный код, а затем из него построить дополнительный.
• Проиллюстрируем это на примере.
• Число - - 101101
• Прямой код - 1101101
• Обратный код - 1010010
• +1
• Дополнительный - 1010011

11101 + 1 = 11110 1 - 11110 + 1 = 11111 0 - 11111 + 1 = (1)00000 (перенос отбрасывается) +1 - 00000 + 1 = 00001 +2 - 00001 + 1 = 00010" width="640"

• Примеры записи.
• Изображаемое число Код
• +1101 (+13) 0000 1101 ( В примерах коды )
• +1011101 (+93) 0101 1101 ( изображаются )
• 1101 (-13) 1111 0011 ( восемью цифрами )
• В дополнительном коде, в отличие от обратного, ноль изображается только одной комбинацией, и кроме этого, достаточно естественно получается переход через ноль, если иметь в виду, что любое число, большее другого на 1, получается при прибавлении к этому другому 1 по правилам сложения. Применительно к дополнительному коду это именно так, если принять к сведению, что разрядность слова фиксирована, и единица переноса из старшего разряда теряется, поскольку ее некуда записать:
• 2 - 11101 + 1 = 11110
• 1 - 11110 + 1 = 11111
• 0 - 11111 + 1 = (1)00000 (перенос отбрасывается)
• +1 - 00000 + 1 = 00001
• +2 - 00001 + 1 = 00010

• Для восстановления прямого кода числа из дополнительного нужно полностью повторить (и именно в том же порядке!) действия, которые использовались при переводе из прямого в дополнительный код: сначала все цифры, кроме цифры, изображающей знак, заменить на противоположные, а затем прибавить 1.
• Основным достоинством дополнительного кода является то, что в нем единообразно реализуются операции сложения чисел разных знаков (алгебраическое сложение), а операцию вычитания можно свести к операции сложения заменой знака вычитаемого на обратный. Вспомнив, что в памяти ЭВМ числа хранятся в прямом коде, станет ясно, что замена знака вычитаемого может быть выполнена чрезвычайно просто (заменой знака числа в прямом коде на обратный). Именно по указанной причине дополнительный код применяется чаще обратного.

• Сложение и вычитание чисел в обратном и дополнительном кодах выполняется с использованием обычного правила арифметического сложения многоразрядных чисел. Общей для этих кодов особенностью (и очень удобной особенностью) является лишь то, что при поразрядном сложении чисел разряды, изображающие знаки чисел рассматриваются как равноправные разряды двоичного числа, которые складываются друг с другом и с единицей переноса из предыдущего разряда числа по обычным правилам арифметики. Различия же обратного и дополнительного кодов связаны с тем, что делается с единицей переноса из старшего разряда (изображающего, как неоднократно говорилось, знак числа).
• При сложении чисел в дополнительном коде единица переноса из старшего разряда игнорируется (теряется), а в обратном коде эту единицу надо прибавить к младшему разряду результата.

+12 -5 Двоичная форма - +1100 -101 Прямой код - 00001100 10000101 Обратный код - 00001100 11111010 Выполним сложение в столбик: 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 0 =============== (1) 0 0 0 0 0 1 1 0 + 1 (Добавление 1 переноса) ============== 0 0 0 0 0 1 1 1 Итак, результат в обратном коде = 00000111. Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7. Проверка (+12-5=+7) показывает, что результат верный." width="640"

• Пример 1. Сложить числа +12 и -5.
• а) В обратном коде
• Десятичная форма - +12 -5
• Двоичная форма - +1100 -101
• Прямой код - 00001100 10000101
• Обратный код - 00001100 11111010
• Выполним сложение в столбик:
• 0 0 0 0 1 1 0 0
• 1 1 1 1 1 0 1 0
• ===============
• (1) 0 0 0 0 0 1 1 0
• + 1 (Добавление 1 переноса)
• ==============
• 0 0 0 0 0 1 1 1
• Итак, результат в обратном коде = 00000111.
• Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7.
• Проверка (+12-5=+7) показывает, что результат верный.

+12 -5 Двоичная форма - +1100 -101 Прямой код - 00001100 10000101 Обратный код - 00001100 11111010 +1 Дополнительный код - 00001100 11111011 Выполним сложение в столбик: 0 0 0 0 1 1 0 0 1 1 1 1 1 0 1 1 ============ (1) 0 0 0 0 0 1 1 1 (Перенос игнорируется) Итак, результат в дополнительном коде = 00000111. Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7. Проверка (+12-5=+7) показывает, что результат верный." width="640"

• б) В дополнительном коде
• Десятичная форма - +12 -5
• Двоичная форма - +1100 -101
• Прямой код - 00001100 10000101
• Обратный код - 00001100 11111010
• +1
• Дополнительный код - 00001100 11111011
• Выполним сложение в столбик:
• 0 0 0 0 1 1 0 0
• 1 1 1 1 1 0 1 1
• ============
• (1) 0 0 0 0 0 1 1 1
• (Перенос игнорируется) Итак, результат в дополнительном коде = 00000111.
• Поскольку знаковый разряд равен 0, результат положительный, и, следовательно, запись кода числа совпадает с записью прямого кода. Теперь можно восстановить алгебраическую запись результата. Он равен +111 (незначащие нули отброшены), или в десятичной форме +7.
• Проверка (+12-5=+7) показывает, что результат верный.

• Умножение и деление двоичных чисел производится в ЭВМ в прямом коде, а знаки их используются лишь для определения знака результата. Также как и в математике, умножение сводится к операциям сложения и сдвига. Деление выполняется за счет комбинирования сдвигов, вычитаний (в этот момент могут использоваться обратный или дополнительный коды) и сложений.

• Построить прямой код числа

• -10001
• 1100
• -11,01

• Построить обратный код числа

• 1111,01
• -1101,1
• -11,11

• Построить дополнительный код числа

• 11,1101
• -11,011
• -101

• Сложить числа 1101 и -1110 в обратном и дополнительном коде используя 4 разряда. Сделать выводы

• Числа с фиксированной запятой
• В числах с фиксированной запятой положение запятой в разрядной сетке машины заранее обусловлено для всех чисел раз и навсегда. Поэтому в коде числа запятая никак не обозначается. В большинстве машин место запятой подразумевается после последней цифры (справа от нее). А такие числа - целые. При необходимости представлять дробные числа с использованием формы с фиксированной запятой программист должен алгоритмическими средствами обеспечить использование множителя, выполняющего функцию масштабирования (масштабного множителя).
• Определим диапазон представимых чисел.
• Вначале рассмотрим пример, в котором положим, что мы имеем дело с десятичной (а не двоичной) системой счисления, и что для записи абсолютной величины числа (без учета его знака) в нашем распоряжении имеется шесть разрядов.

• Тогда максимальное (по абсолютной величине) целое будет равно 999999 или иначе 10**6-1. А поскольку в разрядной сетке машины для записи знака числа всегда предусматривается один разряд, то для нашего случая диапазон представимых чисел составит все целые числа, начиная от
• -999999 до +999999, а количество различных целых - 2*10**6-1.
• В двоичных ЭВМ их разрядность определяется числом разрядов в слове. Так, если разрядность некоторой ЭВМ равна 16, то один разряд отводится для кодирования знака числа, а остальные 15 - для записи его величины. При этом максимальное по модулю целое значение в машинном слове будет равно 2**15-1, что составит 32767. (Посмотрите диапазон целых ( integer ) чисел в языке программирования Паскаль для ПЭВМ типа IMB PC).
• В общем случае, если разрядность машины составляет N битов. Тогда максимальное по абсолютной величине целое число, которое можно в ней записать, будет равно 2**(N-1)-1.

• Особенности арифметических операций над числами
• Поскольку (если положение запятой фиксировано после последней цифры числа) числа с фиксированной запятой - целые, они представляются в машине точно. А потому операции сложения, вычитания и умножения корректны всегда: как операнды, так и результат - целые числа.
• Единственной особенностью, о которой необходимо упомянуть, является ситуация, которая носит название “переполнение разрядной сетки” (FixedOverflow - переполнение с фиксированной запятой) и которая возникает, когда результат умножения превышает максимально возможное для данной разрядности значение. Эта ситуация считается в ЭВМ исключительной. При ее возникновении записать получившееся значение невозможно. В этом случае устанавливается в “1” специальный флаг переполнения, старший бит результата (бит переноса из старшего разряда слова) теряется, а в качестве результата выдается искаженное число. Описываемая ситуация не считается критической, и после окончания данной операции вычисления продолжаются.

• Числа с плавающей запятой
• В форме с плавающей запятой число представляется двумя компонентами : мантиссой и порядком. Мантисса используется для записи цифр числа, а порядок - для указания положения запятой.
• Разрядная сетка машины в этом случае делится на несколько частей:
• один разряд - для кодирования знака числа (это всегда самый старший, левый, разряд слова);
• M разрядов - для записи мантиссы;
• Р разрядов - для записи порядка (с учетом его знака).
• Местоположение запятой при этом тоже строго фиксируется: считается, что мантисса всегда представляется как число, меньшее единицы, но такое, в котором первая цифра после запятой для всех абсолютно чисел отлична от нуля (единственное исключение составляет число 0). Такая форма представления мантиссы называется нормализованной. Иначе говорят, что мантисса нормализована (приведена к виду: 1

• Ну, а если известно, что мантисса имеет вид “0,цццц..”, то ее код в машинном слове может не содержать символов “0,”, а местоположение запятой предполагается перед старшей значащей цифрой мантиссы.
• Порядок Р всегда представляется целым числом со знаком + или -. А для кодирования абсолютной величины порядка остается (Р-1) цифр.
• Теперь можно рассмотреть диапазон представимых чисел.
• Вначале рассмотрим пример применительно к двоичной системе счисления.
• Пусть m - количество разрядов мантиссы,
• р - количество разрядов порядка, включая знаковый.
• Тогда максимальное по абсолютной величине число будет равно
• 0, 1111..1 * 2**(+ 111..1 ) = (1-2**(-м))*2**(2**(р-1)-1),
• m цифр (p-1) цифр
• или приблизительно 2**(2**(р-1)-1),
• а минимальное по абсолютной величине число
• 0, 1000..0 * 2**(- 111..1 ) = 2**(-2**(р-1)).
• m цифр (p-1) цифр

• Итак, число в форме с плавающей запятой представляется последовательностью битов без каких либо явно указанных разделителей, но функционально разбитой на три группы {(знак числа, мантисса числа, порядок числа) или (знак числа, порядок числа, мантисса числа)}.
• Рассмотренная форма кодирования числа приводит к следующим последствиям:
• Диапазон чисел, представимых в форме с плавающей запятой, определяется главным образом разрядностью порядка (Р).
• Разрядность мантиссы (М) определяет точное количество значащих цифр в изображении числа.
• Следовательно, большинство чисел в форме с плавающей запятой представляется приближенно и причиной этого является ограниченное число разрядов мантиссы. Величина же абсолютной погрешности при приближенном представлении числа зависит как от абсолютной величины числа, так и от разрядности мантиссы и порядка.

• Рассмотрим примеры. При этом для простоты положим, что числа представляются в десятичной системе счисления, количество цифр мантиссы равно 4, количество цифр порядка - 2, знак порядка записывается как в математике, а знак числа мы не изображаем, полагая все числа положительными.
• Пример 1. Пусть имеется число 12,42=0,1242*10**(+2).
• В заданном формате оно представляется цепочкой символов
• 1 2 4 2 + 0 2
• При этом цепочка “1 2 4 2” представляет мантиссу, т.е. в математическом смысле число 0,1242 , а цепочка “+ 0 2” - порядок - целое положительное число 2.
• Тогда ближайшее большее этого число может быть задано цепочкой
• 1 2 4 3 + 0 2
• и оно равно 0,1243*10**(+2)= 12,43.
• Таким образом, ближайшие числа на числовой оси, которые различимы при кодировании их в форме с плавающей запятой для данного примера различаются на 0,01 (абсолютная погрешность представления всех чисел между 12,42 и 12,43 имеет верхнюю оценку 0,01).

• Пример 2. Пусть имеется число 0,001242=0,1242*10**(-2).
• В заданном формате оно представляется цепочкой символов
• 1 2 4 2 - 0 2 , а ближайшее большее этого число представляется цепочкой 1 2 4 3 - 0 2
• и равно 0,1243*10**(-2)= 0,001243.
• Таким образом, абсолютная погрешность представления всех чисел между 0,001242 и 0,001243 имеет верхнюю оценку 0,000001.
• Пример 3. Пусть имеется число 0,1242*10**(+12).
• В естественной форме записи это число 124 200 000 000, а в заданном формате оно представляется цепочкой символов
• 1 2 4 2 + 1 2 , а ближайшее большее этого число представляется цепочкой 1 2 4 3 + 1 2
• и равно 0,1243*10**(+12)= 124 300 000 000.
• Таким образом, абсолютная погрешность представления всех чисел между 124 200 000 000 и 124 300 000 000 имеет верхнюю оценку 100 000 000 = 10**8.

• Важный вывод, который следует из анализа формы кодирования чисел с плавающей запятой и иллюстрируется в рассмотренных примерах: числа в форме с плавающей запятой, несмотря на то что, эта форма предложена для представления в ЭВМ непрерывных величин, представляются дискретным множеством на числовой оси и располагаются на ней неравномерно.
• область 1: ХМаксВещ - ни одного значения из области нельзя представить в машинном слове ( МаксВещ - максимальное по абсолютной величине число, которое можно закодировать);
• область 2: - МаксВещ -МинВещ - в данном интервале может быть представлено столько различных чисел, сколько их можно записать по заданной разрядности мантиссы и порядка;
• область 3: -МинВещ 0 - ни одного значения из этой области представить в машинном слове нельзя;
• область 4: 0 +МинВещ - ни одного значения из этой области представить в машинном слове нельзя;

=X= +МаксВещ - в данном интервале может быть представлено столько различных чисел, сколько их можно записать по заданной разрядности мантиссы и порядка; область 6: X +МаксВещ - ни одного значения из области нельзя представить в машинном слове (МаксВещ - максимальное по абсолютной величине число, которое можно закодировать). Особое место занимает величина 0 . Она также кодируется в форме с плавающей запятой, причем как ее порядок, так и мантисса(!) полагаются равными нулю." width="640"

• область 5: +МинВещ =X= +МаксВещ - в данном интервале может быть представлено столько различных чисел, сколько их можно записать по заданной разрядности мантиссы и порядка;
• область 6: X +МаксВещ - ни одного значения из области нельзя представить в машинном слове (МаксВещ - максимальное по абсолютной величине число, которое можно закодировать).
• Особое место занимает величина 0 . Она также кодируется в форме с плавающей запятой, причем как ее порядок, так и мантисса(!) полагаются равными нулю.

• Особенности арифметических операций над числами
• При выполнении арифметических операций все четыре действия арифметики корректны. Следует однако иметь в виду, что дискретный характер представления чисел в форме с плавающей запятой и разбиение числовой оси на области, в ряде из которых невозможно представить ни одного числа, приводит:
• Во-первых, к тому, что при выполнении арифметической операции теоретически возможно формирование результата, который попадает в области 2 или 5, но который нельзя закодировать в форме с плавающей запятой точно. В этом случае, результат заменяется ближайшим из множества допустимых значений с учетом правила округления (ошибка метода представления чисел, вызванная ограниченной разрядностью мантиссы).
• Во-вторых, к тому, что при выполнении арифметической операции теоретически возможно формирование результата, который попадает в область 1 или в область 6. Этот случай является критическим, поскольку результат представить нельзя принципиально. Рассматриваемая ситуация называется “Переполнение с плавающей запятой” (Overflow), а при ее возникновении происходит аппаратное прерывание работы ЭВМ и выполнение программы аварийно прекращается. Причиной этого является ограниченная разрядность порядка.

• В-третьих, к тому, что при выполнении арифметической операции теоретически возможно формирование результата, который попадает в область 3 или в область 4. Рассматриваемая ситуация называется “Потеря значимости”, а при ее возникновении результат заменяется ближайшим допустимым, как правило нулем. Выполнение программы после этого продолжается. Причиной этой ситуации также является ограниченная разрядность порядка.
• В заключении отметим, что при выполнении арифметических операций мантиссы чисел и их порядки обрабатываются по разным алгоритмам. При этом в операциях сложения и вычитания чисел порядки выравниваются за счет сдвига мантиссы меньшего операнда на число разрядов, равное разнице порядков операндов, а в операциях умножения и деления порядки чисел соответственно складывают или вычитают. Поскольку, как мы уже видели раньше, вычитание алгебраических чисел (т.е. с учетом их знаков) в прямом коде реализовать не просто, а порядки представляются как числа целые со знаком в прямом коде, в ряде ЭВМ при представлении числа с плавающей запятой порядок числа заменяется его характеристикой.

• Представьте следующие числа без знака в формате с фиксированной точкой в однобайтовой разрядной сетке. А)15 10 ; Б)30 10 .
• Представьте следующие числа со знаком в двухбайтовой разрядной сетке в формате с фиксированной точкой.А)+15 10 , -15 10 ; Б)+30 10 , -30 10 .
• Представьте следующие числа в формате с плавающей точкой и нормализованной мантиссой:

• 0,001289 10
• 987,2301 10
• 0,01011 2
• 101,001 2

• Представьте двоичные числа из задачи №3 в четырехбайтовой разрядной сетке.

• 0,010111*10 -1
• 0,11010011*10 100

• Для представления информации в памяти ЭВМ (как числовой, так и нечисловой) используется двоичный способ кодирования.
• Элементарная ячейка памяти ЭВМ имеет длину 8 бит (байт). Каждый байт имеет свой номер (его называют адресом). Наибольшую последовательность бит, которую ЭВМ может обрабатывать как единое целое, называют машинным словом. Длина машинного слова зависит от разрядности процессора и может быть равной 16, 32 битам и т.д.
• В некоторых случаях при представлении в памяти ЭВМ чисел используется смешанная двоично-десятичная «система счисления», где для хранения каждого десятичного знака нужен полубайт (4 бита) и десятичные цифры от 0 до 9 представ­ляются соответствующими двоичными числами от 0000 до 1001. Например, упако­ванный десятичный формат, предназначенный для хранения целых чисел с 18 значащими цифрами и занимающий в памяти 10 байт (старший из которых знаковый), использует именно этот вариант.

• Другой способ представления целых чисел — дополнительный код. Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Например, величины типа Integer (все названия типов данных здесь и ниже представлены в том виде, в каком они приняты в языке программирования Turbo Pascal , в других языках такие типы данных тоже есть, но могут иметь другие названия) лежат в диапазоне от -32768 (- 2 15 ) до 32767 (2 15 - 1), и для их хранения отводится 2 байта; типа Longint — в диапазоне от - 2 31 до 2 31 - 1 и размещаются в 4 байтах; типа Word — в диапазоне от 0 до 65535 (2 16 - 1) (используется 2 байта) и т.д.
• Как видно из примеров, данные могут быть интерпретированы как числа со знаками, так и без знаков. В случае представления величины со знаком самый левый (старший) разряд указывает на положительное число, если содержит нуль, и на отрицательное, если — единицу.
• Вообще разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.

• Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число. Например, если число 37 (10) = 100101 (2) объявлено величиной типа Integer , то его прямым кодом будет 0000000000100101, а если величиной типа Longlnt , то его прямой код будет 00000000000000000000000000100101. Для более компактной записи чаще используют шестнадцатеричный код. Полученные коды можно переписать соответственно как 0025 (16) и 00000025 (16) .
• Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:
• 1) записать прямой код модуля числа;
• 2) инвертировать его (заменить единицы нулями, нули — единицами);
• 3) прибавить к инверсному коду единицу.

• Например, запишем дополнительный код числа (-37), интерпретируя его как величину типа Longlnt :
• 1) прямой код числа 37 есть 00000000000000000000000000100101;
• 2) инверсный код 11111111111111111111111111011010;
• 3) дополнительный код 11111111111111111111111111011011 или FFFFFFDB (16). При получении числа по его дополнительному коду прежде всего необходимо:
• определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:
• 1) вычесть из кода числа 1;
• 2) инвертировать код;
• 3) перевести в десятичную систему счисления. Полученное число записать со знаком минус.

• Примеры. Запишем числа, соответствующие дополнительным кодам:
• а) 0000000000010111. Поскольку в старшем разряде записан нуль, то результат будет положительным. Это код числа 23;
• б) 1111111111000000. Здесь записан код отрицательного числа. Исполняем алгоритм:
• 1) 1111111111000000 (2) - 1 (2) = 1111111110111111 (2) ;
• 2) 0000000001000000;
• 3) 1000000 (2) = 64 (10) . Ответ: - 64.

• Несколько иной способ применяется для представления в памяти персонального компьютера действительных чисел. Рассмотрим представление величин с плавающей точкой.
• Любое действительное число можно записать в стандартном виде M *10 P , где 1

• В приведенной выше записи М называют мантиссой числа, а р — его порядком. Для того чтобы сохранить максимальную точность, вычислительные машины по­чти всегда хранят мантиссу в нормализованном виде, что означает, что мантисса в данном случае есть число, лежащее между 1 (10) и 2 (10) , (1
• Персональный компьютер IBM PC позволяет работать со следующими действительными типами (диапазон значений указан по абсолютной величине):

• Покажем преобразование действительного числа для представления его в памяти ЭВМ на примере величины типа Double .
• Как видно из таблицы, величина это типа занимает в памяти 8 байт. На рисунке показано, как здесь представлены поля мантиссы и порядка:
• Можно заметить, что старший бит, отведенный под мантиссу, имеет номер 51, т.е. мантисса занимает младшие 52 бита. Черта указывает здесь на положение двоичной запятой. Перед запятой должен стоять бит целой части мантиссы, но поскольку она всегда равна 1, здесь данный бит не требуется и соответствующий Разряд отсутствует в памяти (но он подразумевается). Значение порядка для упрощения вычислений и сравнения действительных чисел хранится в виде смещенного числа, т.е. к настоящему значению порядка перед записью его в память прибавляется смещение. Смещение выбирается так, чтобы минимальному значению порядка соответствовал нуль.

• Например, для типа Double порядок занимает 11 бит и имеет диапазон от 2 -1023 до 2 1023 , поэтому смещение равно 1023 (10) = 1111111111 (2) . Наконец, бит с номером 63 указывает на знак числа.
• Таким образом, из вышесказанного вытекает следующий алгоритм для получения представления действительного числа в памяти ЭВМ:
• 1) перевести модуль данного числа в двоичную систему счисления;
• 2) нормализовать двоичное число, т.е. записать в виде М*2 Р , где М— мантисса (ее целая часть равна 1 (2) и р — порядок, записанный в десятичной системе счисления;
• 3) прибавить к порядку смещение и перевести смещенный порядок в двоичную систему счисления;
• 4) учитывая знак заданного числа (0 — положительное; 1 — отрицательное), выписать его представление в памяти ЭВМ.

• Пример. Запишем код числа -312,3125.
• 1) Двоичная запись модуля этого числа имеет вид 100111000,0101.
• 2) Имеем 100111000,0101 = 1,001110000101*2 8 .
• 3) Получаем смещенный порядок 8 + 1023 = 1031. Далее имеем 1031 (10) = 10000000111 (2) .
• очевидно, что более компактно полученный код стоит записать следующим образом: С073850000000000(16).
• 4) Окончательно
• Другой пример иллюстрирует обратный переход от кода действительного числа к самому числу.

0 10000000111 0011100001010000000000000000000000000000000000000000

63 52 0

• Пример. Пусть дан код 3 FEC 60000000000(16) или
• 1) Прежде всего замечаем, что это код положительного числа, поскольку в разряде с номером 63 записан нуль. Получим порядок этого числа: 01111111110 (2) = 1022 (10) ; 1022- 1023 = -1.
• 2) Число имеет вид 1,1100011*2 -1 или 0,11100011.
• 3) Переводом в десятичную систему счисления получаем 0,88671875.

0 10000000111 1100011000000000000000000000000000000000000000000000

63 52 0

• 1.Переведите данное число из десятичной системы счисления в двоично-десятичную.
• 2.Переведите данное число из двоично-десятичной системы счисления в десятичную.
• 3.Запишите прямой код числа, интерпретируя его как восьмибитовое целое без знака.
• 4.Запишите дополнительный код числа, интерпретируя его как восьмибитовое целое со знаком.
• 5.Запишите прямой код числа, интерпретируя его как шестнадцатибитовое целое без знака.
• 6.Запишите дополнительный код числа, интерпретируя его как шестнадцатибитовое целое со знаком.
• 7.Запишите в десятичной системе счисления целое число, если дан его дополнительный код.
• 8. Запишите код действительного числа, интерпретируя его как величину типа Double .
• 9. Дан код величины типа Double . Преобразуйте его в число.

Вариант 1

• а) 585 (10) ; б) 673 (10) ; в) 626 (10) .
• а) 010101010101 (2-10) ; б) 10011000 (2-10) ; в) 0100000101 10 (2 -1 0) .
• а) 224 (10) ; б) 253 (10) ; в) 226 (10) .
• а) 115 (10) ; б) -34 (10) ; в) -70 (10) .
• а) 22491 (10) ; б) 23832 (10) .
• а) 20850 (10) ; б) -18641 (10) .
• а) 0011010111010110; б) 1000000110101110.
• а) -578,375; б) -786,375.
• а) 408Е130000000000; б) С077880000000000.

Вариант 2

• а) 285 (10) ; б) 846 (10) ; в) 163 (10) .
• а) 000101010001 (2-10) ; б) 010101010011 (2-10) ; в) 011010001000 (2-10) .
• а) 242 (10) ; б) 135 (10) ; в) 248 (10) .
• а) 81 (10) ; б) -40 (10) ; в) -24 (10) .
• а) 18509 (10) ; б) 28180 (10) .
• а) 28882 (10) ; б) -19070 (10) .
• а) 0110010010010101; б) 1000011111110001.
• а) -363,15625; б) -487,15625.
• а) С075228000000000; б) 408В9В0000000000

Вариант 3

• а) 905 (10) ; б) 504 (10) ; в) 515 (10) .
• а) 010010010100 (2-10) ; б) 001000000100 (2 -1 0) ; в) 01110000 (2-10) .
• а) 207 (10) ; б) 210 (10) ; в) 226 (10) .
• а) 98 (10) ; б) -111 (10) ; в) -95 (10) .
• а) 19835 (10) ; б) 22248 (10)
• а) 18156 (10) ; б) -28844 (10) .
• а) 0111100011001000; б) 1111011101101101.
• а) 334,15625; б) 367,15625.
• а) С07С08С000000000; б) С0811В0000000000.

Вариант 4

• а) 483 (10) ; б) 412 (10) ; в) 738 (10) .
• а) 001101011000 (2-10) ; б) 100010010010 (2-10) ; в) 010101000110 (2-10) .
• а) 185 (10) ; б) 224 (10) ; в) 193 (10) .
• а) 89 (10) ; б) -65 (10) ; в) -8 (10) .
• а) 29407 (10) ; б) 25342 (10) .
• а) 23641 (10) ; б) -23070 (10) .
• а) 0111011101000111; б) 1010110110101110.
• а) 215,15625; б) -143,375.
• а) С071760000000000; б) 407FF28000000000.

Вариант 5

• а) 88 (10) ; б) 153 (10) ; в) 718 (10) .
• а) 000110000100 (2-10) ; б) 100110000111 (2-10) ; в) 100100011000 (2-10) .
• а) 158 (10) ; б) 134 (10) ; в) 190 (10) .
• а) 64 (10) ; б) -104 (10) ; в) -47 (10) .
• а) 30539 (10) ; б) 26147 (10) .
• а) 22583 (10) ; б) -28122 (10) .
• а) 0100011011110111; б) 1011101001100000.
• а) -900,546875; б) -834,5.
• а) 407С060000000000; б) C061 0 C 0000000000 .

Вариант 6

• а) 325 (10) ; б) 112 (10) ; в) 713 (10) .
• а) 100101100010 (2-10) ; б) 001001000110 (2-10) ; в) 011100110110 (2-10) .
• а) 239 (10) ; б) 160 (10) ; в) 182 (10) .
• а) 55 (10) ; б) -89 (10) ; в) -22 (10) .
• а) 17863 (10) ; б) 25893 (10) .
• а) 24255 (10) ; б) -26686 (10) .
• а) 0000010101011010; б) 1001110100001011.
• а) -969,15625; б) -434,15625.
• а) С082ВЗ0000000000; б) С086ЕВ0000000000.

Вариант 7

• а) 464 (10) ; б) 652 (10) ; в) 93 (10) .
• а) 000110010010 (2-10) ; б) 001100011000 (2-10) ; в) 011000010000 (2-10) .
• а) 237 (10) ; б) 236 (10) ; в) 240 (10) .
• а) 95 (10) ; б) -68 (10) ; в) -77 ( 10 ) .
• а) 28658 (10) ; б) 29614 (10) .
• а) 31014 (10) ; б) -24013 (10) .
• а) 0001101111111001; б) 1011101101001101.
• а) -802,15625; б) -172,375.
• а) С085ЕВ0000000000; б) C07D428000000000.

Вариант 8

• а) 342 (10) ; б) 758 (10) ; в) 430 (10) .
• а) 010110010000 (2-10) ; б) 011101100101 (2-10) ;в) 011100010111 (2-10) .
• а) 136 (10) ; б) 130 (10) ; в) 239 (10) .
• а) 82 (10) ; б) -13 (10) ; в) -77 (10) .
• а) 27898 (10) ; б) 24268 (10) .
• а) 19518 (10) ; б) -16334 (10) .
• а) 0000110100001001; б) 1001110011000000.
• а) 635,5; б) -555,15625.
• а) С07848С000000000; б) С085394000000000.

Вариант 9

• а) 749 (10) ; б) 691 (10) ; в) 1039 (10) .
• а) 100100010001 (2-10) ; б)001000111001 (2-10) ; в) 001101100011 (2-10) .
• а) 230 (10) ; б) 150 (10) ; в) 155 (10) .
• а) 74 (10) ; б) -43 (10) ; в) -21 (10) .
• а) 18346 (10) ; б) 25688 (10) .
• а) 31397 (10) ; б) -21029 ( 10 ) .
• а) 0110101101111000; б) 1110100100110101.
• а) 110,546875; б) -743,375.
• а) С08В794000000000; б) 407СВ28000000000.

Вариант 10

• а) 817 (10) ; б) 661 (10) ; в) 491 (10) .
• а) 100001010001 (2-10) ; б)010000000111 (2-10) ; в) 001001110001 (2-10) .
• а) 219 (10) ; б) 240 (10) ; в) 202 (10) .
• а) 44 (10) ; б) -43 (10) ; в) -94 (10) .
• а) 23359 (10) ; б) 27428 (10) .
• а) 21481 (10) ; б) -20704 (10) .
• а) 0001101010101010; б) 1011110111001011.
• а) -141,375; б) 145,375.
• а) 408ЕА14000000000; б) С07В128000000000.

Вариант 11

• а) 596 (10) ; б) 300 (10) ; в) 515 (10) .
• а) 001100100110 (2-10) ; б) 001000010110 (2-10) ; в) 010100010010 (2-10) .
• а) 237 (10) ; б) 160 (10) ; в) 253 (10) .
• а) 122 (10) ; б) -97 (10) ; в) -82 (10) .
• а) 30469 (10) ; б) 21517 (10) .
• а) 23008 (10) ; б) -23156 (10) .
• а) 0010111101000000; б) 1011001101110001.
• а) 576,375; б) -99,375.
• а) 40864В0000000000; б) С047140000000000.

Вариант 12

• а) 322 (10) ; б) 320 (10) ; в) 738 (10) .
• а) 000110000000 (2-10) ; б) 100101010110 (2-10) ; в) 011101100001 (2-10) .
• a) 201 (10) ; б) 135 (10) ; в) 198 (10) .
• a) 91 ( 10 ) ; б) -7 (10) ; в) -95 (10) .
• a) 29234 (10) ; б) 19909 ( 10 ) .
• a) 25879 ( 10 ) ; б) -27169 (10) .
• a) 0001111001010100; 6) 1011010001110010.
• a) -796,15625; б) 325,15625.
• a) 4060B 00000000000 ; б) С0846С6000000000.

Вариант 13

• a) 780 (10) ; б) 949 (10) ; в) 718 (10) .
• a) 0001000000010101 (2 - 10) ; б) 100110011001 (2-10) ; в)001101100001 (2-10) .
• a) 188 (10) ; б) 213 (10) ; в) 217 (10) .
• a) 89 (10) ; б) -90 (10) ; в) -34 (10) .
• a) 25173 (10) ; б) 25416 (10) .
• a) 27435 (10) ; б) -22433 (10) .
• a) 0111110101101100; б) 1111011001100010.
• a) -142,375; б) 565,15625.
• a) C086494000000000; б) C083DC6000000000.

Вариант 14

• a) 164 (10) ; б) 1020 (10) ; в) 713 (10) .
• a) 0111 10000100 (2 - 10) ; б) 00110001000 1 (2 - 10) ; в) 100101010001 (2-10) .
• a) 127 (10) ; б) 199 (10) ; в) 187 (10) .
• a) 57 (10) ; б) -31 (10) ; в) -109 ( 10 ) .
• a) 17689 ( 10 ) ; б) 20461 (10) .
• a) 26493 (10) ; б) -30785 (10) .
• а) 0010110001100110; б) 1010001111010000.
• а) -550,15625; б) 616,15625.
• а) 407С360000000000; б) 408В594000000000.

Вариант 15

• а) 280 (10) ; б) 700 (10) ; в) 464 (10) .
• а) 010100110011 (2-10) ; б) 100100100101 (2-10) ; в) 100010010001 (2-10) .
• а) 217 (10) ; б) 161 (10) ; в) 232 (10) .
• а) 53 (10) ; б) -24 (10) ; в) -110 (10) .
• а) 23380 (10) ; б) 22620 (10) .
• а) 24236 (10) ; б) -30388 (10) .
• а) 0100101101100011; б) 1001001000101100.
• а) 84,15625; б) -681,375.
• а) 4075Е28000000000; б) С07Е980000000000.

Вариант 16

• а) 728 (10) ; б) 383 (10) ; в) 202 (10) .
• а) 001100110011 (2-10) ; б) 001101100010 (2-10) ; в) 010001000100 (2-10) .
• а) 170 (10) ; б) 242 (10) ; в) 158 (10) .
• а) 70 (10) ; б) -50 (10) ; в) -90 (10) .
• а) 21581 (10) ; б) 31014 (10) .
• а) 19903 (10) ; б) -17431 (10) .
• а) 0011111110001000; б) 1001011111011111.
• а) 650,375; б) -974,5.
• a) C05DCA 0000000000 ; б) 408Е5В0000000000

Вариант 17

• а) 158 (10) ; б) 177 (10) ; в) 439 (10) .
• а) 000100110101 (2-10) ; б) 001010010011 (2-10) ;в) 0001000000100100 (2-10) .
• а) 172 (10) ; б) 247 (10) ; в) 216 (10) .
• а) 104 (10) ; б) -67 (10) ; в) -88 (10) .
• а) 17134 (10) ; б) 17996 (10) .
• а) 24197 (10) ; б) -19851 (10) .
• а) 0001010110011011; б) 1001010000111010.
• а) 423,15625; б) 835,15625.
• а) 4089794000000000; б) 408В414000000000.

Вариант 18

• а) 328 (10) ; б) 537 (10) ; в) 634 (10) .
• а) 000100000100 (2-10) ; б) 010110011001 (2-10) ; в) 100000110111 (2-10) .
• а) 203 (10) ; б) 199 (10) ; в) 214 (10) .
• а) 87 (10) ; б) -50 (10) ; в) -31 (10) .
• а) 17130 (10) ; б) 27910 (10) .
• а) 26837 (10) ; б) -17264 (10) .
• а) 0100011000011101; б) 1101001111000101.
• а) -197,15625; б) -341,375.
• a) C057D80000000000; б) 406F 0 C 0000000000 .

Вариант 19

• а) 1026 (10) ; б) 725 (10) ; в) 100 (10) .
• а) 100110010110 (2-10) ; б) 100100110010 (2-10) ; в) 000110010000 (2 -10 ) .
• а) 173 (10) ; б) 149 (10) ; в) 129 (10) .
• а) 73 (10) ; б) -117 (10) ; в) -39 (10) .
• а) 24335 (10) ; б) 28591 (10) .
• а) 19650 (10) ; б) -27052 (10) .
• а) 0110010000000000; б) 1111111001010100.
• а) 612,15625; б) -652,546875.
• а) 40664С0000000000; б) 40684С0000000000.

Вариант 20

• а) 853 (10) ; б) 135 (10) ; в) 66 (10) .
• а) 100001111001 (2-10) ; б) 100000010000 (2-10) ; в) 001101000100 (2-10) .
• а) 178 (10) ; б) 240 (10) ; в) 152 (10) .
• а) 54 (10) ; б) -10 (10) ; в) -43 (1 0) .
• а) 18083 (10) ; б) 19157 (10) .
• а) 18477 (10) ; б) -28803 (10) .
• а) 0101010001100111; б) 1110101001001100.
• а) 575,375; б) 983,375.
• а) С088440000000000; б) С0696С0000000000.

Вариант 21

• а) 206 (10) ; б) 382 (10) ; в) 277 (10) .
• а) 011101100101 (2-10) ; б) 010001110111 (2-10) ; в) 011101010000 (2-10) .
• а) 234 (10) ; б) 254 (10) ; в) 192 (10) .
• а) 120 (10) ; б) -110 (10) ; в) -112 (10) .
• а) 19743 (10) ; б) 30381 (10) .
• а) 30643 (10) ; б) -23233 (10) .
• а) 0111100111001110; б) 1001100000100111.
• а) -503,15625; б) 339,375.
• а) С06ЕА50000000000; б) С08Е230000000000.

Вариант 22

• а) 692 (10) ; б) 844 (10) ; в) 1014 (10) .
• а) 010101100010 (2-10) ; б) 100100100111 (2-10) ; в) 001001000101 (2-10) .
• a) 215 (10) ; б) 229 (10) ; в) 241 (10) .
• a) 101 ( 10 ) ; б) -34 (10) ; в) -56 (10) .
• a) 23242 (10) ; б) 17599 (10) .
• a) 25657 (10) ; б) -29323 (10) .
• a) 0010101000011001; б) 1011000010001010.
• a) 654,546875; б) 494,375.
• a) C0642C 0000000000 ; б) C082F14000000000.

Вариант 23

• a) 707 (10) ; б) 133 (10) ; в) 1023 (10) .
• a) 0010100000 11 (2 -1 0) ; б) 010000000011 (2-10) ; в) 001010000001 (2-10) .
• a) 136 (10) ; б) 202 (10) ; в) 207 (10) .
• a) 85 ( 10 ) ; б) -44 (10) ; в) -66 (10) .
• а) 17949 (10) ; б) 27584 (10) .
• a) 27445 (10) ; б) -31187 (10) .
• a) 0100011111000100; б) 1011001111110000.
• 446,15625; б) -455,375.
• а) 408B894000000000; б) С089930000000000.

Вариант 24

• a) 585 (10) ; б) 239 (10) ; в) 361 (10) .
• a) 011010000001 (2 -1 0) ; б) 100001010001 (2-10) ; в) 0011100001 11 ( 2-10 ) .
• a) 162 (10) ; б) 224 (10) ; в) 206 (10) .
• a) 73 (10) ; б) -111 (10) ; в) -66 (10) .
• a) 17189 ( 10 ) ; б) 22238 (10) .
• a) 32549 (10) ; б) -23508 ( 10 ) .
• a) 0011100011010100; б) 1001010101100011.
• a) -279,375; б) -838,15625.
• а) 4081С94000000000; 6) 403D800000000000.

Вариант 25

• a) 382 (10) ; б) 830 (10) ; в) 512 (10) .
• a) 100000100101 (2 - 10) ; б) 010010010100 (2 - 10) ; в) 011000000011 (2 - 10) .
• a) 136 ( 10 ) ; б) 183 (10) ; в) 162 ( 10 ) .
• a) 111 ( 10 ) ; б) -122 (10) ; в) -61 (10) .
• a) 21736 (10) ; б) 22611 (10) .
• a) 18894 (10) ; б) -25174 ( 10 ) .
• a) 0000111101011000; б) 1110000000001111.
• a) 300,546875; б) -400,15625.
• a) 408EFB 0000000000 ; 6) 4078D28000000000.

• Для кодирования символов достаточно одного байта. При этом можно представить 256 символов (с десятичными кодами от 0 до 255). Набор символов персональных ЭВМ IBM PC чаще всего является расширением кода ASCII ( American Standart Code for Information Interchange — стандартный американский код для обмена информацией).
• Как мы уже выяснили, традиционно для кодирования одного символа используется 8 бит. И, когда люди определились с количеством бит, им ос­талось договориться о том, каким кодом кодировать тот или иной символ, чтобы не получилось путаницы, т.е. необходимо было выработать стандарт — все коды символов сохранить в специальной таблице кодов. В первые годы развития вычислительной техники таких стандартов не существовало, а сейчас наоборот, их стало очень много, но они противоречивы. Первыми решили эти проблемы в США, в Институте стандартизации. Этот институт ввел в действие таблицу кодов ASCII ( American Standard Code for Information Interchange - стандартный кон информационного обмена США).

• Таблица ASCII разделена на две части. Первая - стандартная - содержит коды от 0 до 127. Вторая - расширенная - содержит символы с кодами от 128 до 255.
• Первые 32 кода отданы производителям аппаратных средств и называются они управляющие, т.к. эти коды управляют выводом данных. Им не соответствуют никакие символы.
• Коды с 32 по 127 соответствуют символам английского алфавита, знакам препинания, цифрам, арифметическим действиям и некоторым вспомогательным символам.
• Коды расширенной части таблицы ASCII отданы под символы национальных алфавитов, символы псевдографики и научные символы. Если вы внимательно посмотрите на обе части таблицы то увидите, что все буквы расположены в них по алфавиту, а цифры — по возрастанию. Этот принцип последовательного кодирования позволяет определить код символа, не заглядывая в таблицу.
• Коды цифр берутся из этой таблицы только при вводе и выводе и если они используются в тексте. Если же они участвуют в вычислениях, то переводятся в двоичную систему счисления.

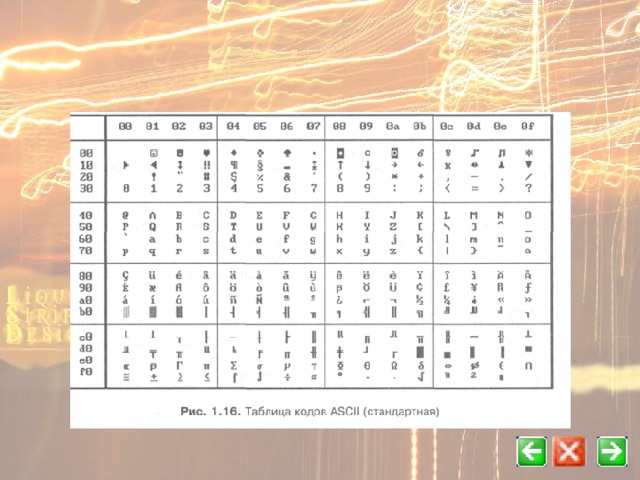
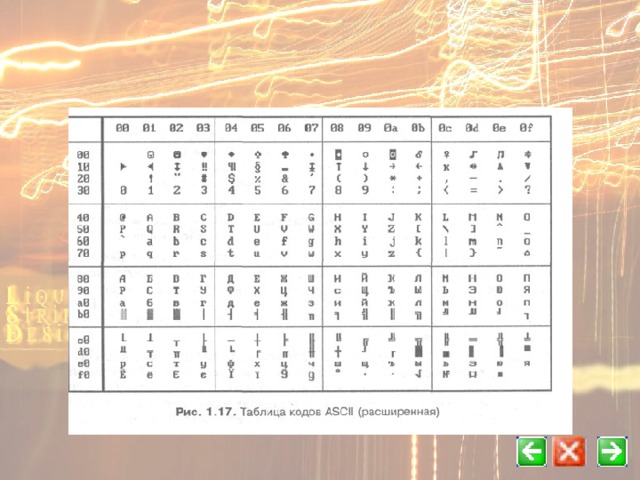
• 1 . Зашифруйте данный текст, используя таблицу ASCII -кодов.
• 2. Дешифруйте данный текст, используя таблицу ASCII -кодов.

Вариант 1

• Задание 1
• IBM PC.
• Задание 2
• 8А АЕ AC AF ЕС ЕЕ Е2 А5 ЕО .

Вариант 2

• Задание 1
• Автоматизация.
• Задание 2
• 50 72 6F 67 72 61 6D.

Вариант 3

• Задание 1
• Информатика.
• Задание 2
• 50 72 6F 63 65 64 75 72 65.

Вариант 4

• Задание 1
• Computer.
• Задание 2
• 84 88 91 8А 8Е 82 8Е 84.

Вариант 5

• Задание 1
• Printer.
• Задание 2
• 43 4F 4D 50 55 54 45 52.

Вариант 6

• Задание 1
• Компьютеризация.
• Задание 2
• 50 52 49 4Е 54.

Вариант 7

• Задание 1
• YAMAHA.
• Задание 2
• 4D4F44454D.

Вариант 8

• Задание 1
• Световое перо.
• Задание 2
• 4С 61 73 65 72.

Вариант 9

• Задание 1
• Микропроцессор.
• Задание 2
• 88 AD Е4 АЕ ЕО АС А0 Е2 А8 АА А0.

Вариант 10

• Задание 1
• Принтер.
• Задание 2
• 42 69 6Е 61 72 79.

Вариант 11

• Задание 1
• Дисковод.
• Задание 2
• 49 6Е 66 6F 72 6D 61 74 69 6F 6Е.

Вариант 12

• Задание 1
• Pentium 100.
• Задание 2
• 91 А 8 El Е 2 А 5 АС А0 20 El Е 7 А 8 El AB A5 AD A8 EF.

Вариант 13

• Задание 1
• Арифмометр.
• Задание 2
• AC AE A4 A5 AB A8 E 0 AE A2 АО AD A8 A5.

Вариант 14

• Задание 1
• Сканер.
• Задание 2
• A2 ЕВ E7 A8 E 1 AB A8 E2 A5 AB EC AD EB A9 20 ED AA E 1 AF A5 E0 A8 AC A5 AD E2.

Вариант 15

• Задание 1
• Винчестер.
• Задание 2
• 43 6F 6D 70 75 74 65 72 20 49 42 4D 20 50 43.

Вариант 16

• Задание 1
• IBM PC.
• Задание 2
• 8А АЕ AC AF ЕС ЕЕ Е2 А5 Е0.

Вариант 17

• Задание 1
• Автоматизация.
• Задание 2
• 50 72 6F 67 72 61 6D.

Вариант 18

• Задание 1
• Информатика.
• Задание 2
• 50 72 6F 63 65 64 75 72 65.

Вариант 19

• Задание 1
• Computer.
• Задание 2
• 84 88 91 8А 8Е 82 8Е 84

Вариант 20

• Задание 1
• Printer.
• Задание 2
• 43 4F 4D 50 55 54 45 52.

Вариант 21

• Задание 1
• Компьютеризация.
• Задание 2
• 50 52 49 4Е 54.

Вариант 22

• Задание 1
• YAMAHA.
• Задание 2
• 4D4F44454D.

Вариант 23

• Задание 1
• Световое перо.
• Задание 2
• 4C 61 73 65 72.

Вариант 24

• Задание 1
• Микропроцессор.
• Задание 2
• 88 AD E4 AE E0 AC А 0 E2 A8 AA А 0.

Вариант 25

• Задание 1
• Принтер.
• Задание 2
• 42 69 6E 61 72 79.

Вариант 1

• 1. Позиция цифры в числе называется:
• 1) кодом;
• 2) разрядом;
• 3) основанием;
• 4) коэффициентом.
• 2. Количество цифр, используемых для записи числа в системе счисления, называют:
• 1) коэффициентом;
• 2) основанием;
• 3) разрядом;
• 4) кодом.

• 3. Каждый разряд машинного двоичного кода несет количество информации, равное:
• 1) 1 биту;
• 2) 2 10 битам;
• 3) 1 байту;
• 4) 2 10 байтам.
• 4. Быстрое увеличение разрядов характерно для системы счисления с основанием:
• 1) 2;
• 2) 8;
• 3) 10;
• 4) 16.

• 5. Десятичное число 5 в двоичной системе счисления записывается как:
• 1)100;
• 2)101;
• 3)110;
• 4)111.
• 6. Максимальное целое число, которое можно записать в трех разрядах, при использовании двоичной системы счисления — это:
• 1) 2;
• 2) 3;
• 3) 7;
• 4) 8.

• 7. Система счисления, в которой 8 + 1 = 10, является:
• 1) двоичной;
• 2) восьмеричной;
• 3) девятеричной;
• 4) десятичной.
• 8. При переводе из двоичной системы счисления в восьмеричную число разбивается на разряды по:
• 1)2 знака;
• 2)3 знака;
• 3)4 знака;
• 4) 5 знаков.

• 9. В учебном центре учатся 213 человек — 122 юноши и 41 девушка. Количество учащихся подсчитано в следующей системе счисления:
• 1) двоичной;
• 2) троичной;
• 3) четверичной
• 4) пятеричной.
• 10. При переводе числа 8 AF 16 в восьмеричную систему счисления получим число:
• 1) 4257;
• 2) 4357;
• 3) 3457;
• 4) 4527.

• 11. При перенесении запятой влево на три знака в 8 раз уменьшится число:
• 1) 300,05 8 ;
• 2) 222,0124;
• 3) 101,0112;
• 4) 201,206.
• 12. Результатом вычитания FF 16 - 1 является число:
• 1)Е4 16 ;
• 2)ЕЕ 16 ;
• 3) FE 16 ;
• 4) F 4 16 .

• 13. Естественная форма представления используется только для чисел следующего вида:
• 1) дробных;
• 2) комплексных;
• 3) целых;
• 4) иррациональных.
• 14. Количество разрядов, занимаемых двухбайтовым числом, равно:
• 1) 8;
• 2) 16;
• 3) 32;
• 4) 64.

• 15 Отрицательный знак числа в разрядной сетке обозначается:
• 1)0;
• 2)1;
• 3)-;
• 4)+.
• 16. Обратный код целого числа образуется инвертированием разрядов числа в коде следующего вида:
• 1) дополнительном;
• 2) обратном;
• 3) прямом;
• 4) естественном.

• 17. При увеличении на единицу младшего разряда обратного кода целого числа, получается код следующего вида:
• 1) прямой;
• 2) обратный;
• 3) дополнительный;
• 4) нормализованный.
• 18. В представлении числа с плавающей точкой в памяти компьютера мантисса может быть:
• 1) буквой;
• 2) целым числом;
• 3) десятичной дробью
• 4) обыкновенной дробью.

• 19. В представлении числа с плавающей точкой порядок числа является:
• 1) целым числом;
• 2) обыкновенной дробью;
• 3) буквой;
• 4) периодической дробью.
• 20.Система счисления — это:
• а)совокупность цифр I, V, X, L, C, D, M;
• б)совокупность цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
• в)совокупность цифр 0, 1;
• г)принятый способ записи чисел;
• д)множество натуральных чисел.

• 21.Укажите самое большое число:
• а) 156 13 ;
• б) 156 10 ;
• в) 156 8 ;
• г) 156 16 ;
• д) 156 12 .
• 22. К достоинствам двоичной системы счисления относят:
• а)простоту совершаемых операций и возможность автоматической обработки информации с использованием только двух состояний элементов компьютера;
• б)широкое использование названной системы в обыденной жизни;
• в)наглядность и понятность записи числа в двоичной системе счисления;
• г)экономию памяти компьютера;
• д)возможность экономии электроэнергии.

• 23.Число 10 (в десятичной системе счисления) в двоичной системе счисления имеет вид:
• а) 100;
• б) 10;
• в) 2;
• г) 1010;
• д) 11.
• 24.Число 10 16 соответствует числу в десятичной системе счисления:
• а) 1010;
• б) 101010;
• в) 1610;
• г) 3210;
• д) 1510.

• 25.Число F 16 соответствует числу в десятичной системе счисления:
• а) 10 10 ;
• б) 1010 10 ;
• в) 16 10 ;
• г) 32 10 ;
• д) 15 10 .
• 26.Число FА 16 соответствует числу в десятичной системе счисления:
• а) 250 10 ;
• б) 256 10 ;
• в) 16 10 ;
• г) 32 10 ;
• д) 1018 10 .

• 27.Число 11010111 2 соответствует числу в восьмеричной системе счисления:
• а) 494 8 ;
• б) 125 8 ;
• в) 76 8 ;
• г) 327 8 ;
• д) 99 8 .
• 28. Отрицательный знак числа в разрядной сетке обозначается:
• 1)0;
• 2)1;
• 3)-;
• 4)+.

• 29. Свойство машинной памяти определять адрес машинного слова по адресу младшего байта, называют:
• 1) дискретностью;
• 2) объемностью;
• 3) адресуемостью;
• 4) размерностью.
• 30. Адреса четырехбайтовых машинных слов меняются с шагом:
• 1)2;
• 2)4;
• 3)8;
• 4)16.

• 1. Во сколько раз различаются значения цифр соседних разрядов числа, определяется:
• 1) степенью;
• 2) основанием;
• 3) алфавитом;
• 4) разрядом.
• 2. Все знаки, используемые для записи числа в системе счисления, называют:
• 1) разрядом;
• 2) основанием;
• 3) алфавитом;
• 4) коэффициентом.

• 3. Количество информации, которое несет один разряд двоичного числа, равно :
• 1) 1 биту;
• 2) 2 10 битам;
• 3) 1 байту;
• 4) 2 10 байтам.
• 4. В алфавите шестнадцатеричной системы счисления по сравнению с десятичной:
• 1) меньше знаков;
• 2) больше знаков;
• 3) нет латинских букв;
• 4) нет цифр.

• 5. Десятичное число 7 в двоичной системе счисления записывается как :
• 1) 100;
• 2) 101;
• 3) 110;
• 4) 111.
• 6. Максимальное целое число, которое можно записать в двух разрядах при использовании двоичной системы счисления — это:
• 1)2;
• 2)3;
• 3)7;
• 4)8.

• 7. Дробь 0,2 5 в десятичной системе выглядит как:
• 1) 0,2;
• 2) 0,4;
• 3) 2,5;
• 4) 5,2.
• 8. При переводе из двоичной системы счисления в шестнадцатеричную, число разбивается на разряды по:
• 1) 2 знака;
• 2) 3 знака;
• 3) 4 знака;
• 4) 5 знаков.

• 9. В саду 111 фруктовых деревьев — 14 яблонь и 42 груши. Деревья посчитаны в следующей системе счисления:
• 1) двоичной;
• 2) четверичной;
• 3) пятеричной;
• 4) десятичной.
• 10. При переводе числа 7ВС 16 в восьмеричную систему счисления получим число:
• 1) 3674;
• 2) 3764;
• 3) 6374;
• 4) 7463.

• 11. Величина числа 310,536, при перенесении запятой на один знак вправо:
• 1) увеличится в 10 раз;
• 2) уменьшится в 10 раз;
• 3) увеличится в 6 раз;
• 4) уменьшится в 6 раз.
• 12. Результатом сложения FF 16 +1, является число:
• 1)100 16 ;
• 2)160 16 ;
• 3) 176 16 ;
• 4) 177 16 .

• 13. Вещественные числа представляются в компьютере в:
• 1) естественной форме;
• 2) нормализованной форме;
• 3) виде ненормализованной десятичной дроби;
• 4) виде обыкновенной дроби.
• 14. Количество разрядов, занимаемых однобайтовым числом, равно:
• 1) 8;
• 2) 16;
• 3) 32;
• 4) 64.

• 15. Положительный знак числа в разрядной сетке обозначается:
• 1)0;
• 2)1;
• 3)-;
• 4)+.
• 16. Дополнительный код отрицательного числа образуется:
• 1) инвертированием разрядов числа;
• 2) прибавлением единицы к младшему разряду обратного кода числа;
• 3) вычитанием единицы из младшего разряда обратного кода числа;
• 4) прибавлением единицы к прямому коду числа.

• 17. В представлении числа с плавающей точкой порядок может быть:
• 1) цифрой;
• 2) целым числом;
• 3) десятичной дробью;
• 4) обыкновенной дробью.
• 18. Наибольшую последовательность битов, обрабатываемую компьютером как единое целое, называют:
• 1) машинным порядком;
• 2) байтом;
• 3) машинным словом;
• 4) адресом.

• 19. Адреса двухбайтовых машинных слов меняются с шагом:
• 1)1;
• 2)2;
• 3)4;
• 4)8.
• 20. Под вещественные числа, представленные в форме с плавающей точкой, традиционно отводится следующее количество разрядов:
• 1) 8;
• 2) 32;
• 3) 16;
• 4) 64.

• 21.Система счисления — это:
• а)знаковая система, в которой числа записываются по определенным правилам с помощью символов (цифр) некоторого алфавита;
• б)произвольная последовательность цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
• в)бесконечна последовательность цифр 0, 1;
• г)совокупность цифр I, V, X, L, C, D, M;
• д)множество натуральных чисел и знаков арифметических действий.
• 22.Укажите самое большое число:
• а)756 10 ;
• б)756 8 ;
• в)756 16 ;

• 23.В позиционной системе счисления
• а)значение каждого знака в числе зависит от значения числа;
• б)значение каждого знака в числе зависит от значений соседних знаков;
• в)значение каждого знака в числе зависит от позиции, которую занимает знак в записи числа;
• г)значение каждого знака в числе не зависит от значения знака в старшем разряде;
• д)значение каждого знака в числе зависит от значения суммы соседних знаков.
• 24Число 10 (в десятичной системе счисления) в двоичной системе счисления имеет вид:
• а) 10;
• б) 1010;
• в) 100;
• г) 11.

• 25.Число 10 16 (в шестнадцатеричной системе счисления) в десятичной системе счисления имеет вид:
• а) 1010;
• б) 16;
• в) 101;
• г) 12;
• д) СD.
• 26.Последовательность знаков 10 2 (число в двоичной системе счисления) в десятичной системе счисления соответствует числу:
• а) 4 10 ;
• б) 2 10 ;
• в) 10 10 ;
• г) 20 10 ;
• д) 8 10 .

• 27.Число А 16 соответствует числу в десятичной системе счисления:
• а) 16;
• б) 10;
• в) 64;
• г) 32;
• д)15.
• 28.Число 20 16 соответствует числу в десятичной системе счисления:
• а) 10 10 ;
• б) 1010 10 ;
• в) 16 10 ;
• г) 32 10 ;
• д) 64 10 .

• 29.Число 10010110 2 соответствует числу в шестнадцатеричной системе счисления:
• а) 94 16 ;
• б) 97 16 ;
• в) 95 16 ;
• г) 96 16 ;
• д) 99 16 .
• 30. Обратный код целого числа в памяти компьютера образуется инвертированием всех двоичных разрядов числа в коде:
• 1) прямом;
• 2) обратном,
• 3) дополнительном .