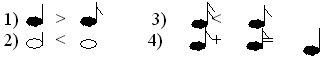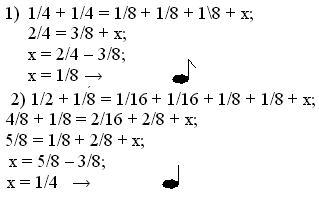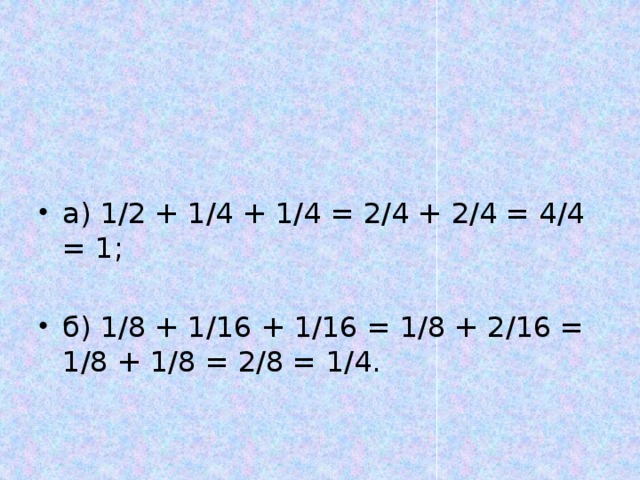Бинарный урок по математике и музыке в 6-м классе по теме "Дроби и ноты"
Закрепление знаний учащихся об обыкновенных дробях (сложение и вычитание дробей с одинаковыми и разными знаменателями, сравнение дробей).
Обобщение понятий о дробях на основе их распространения на ситуации с нотами.
Закрепление видения нот, как своеобразной (без цифровой) знаковой формы дробей.
Расширение кругозора учащихся.
Воспитание интереса и увлечения к изучаемому предмету.
Оборудование.
Ход урока
1. Организационный момент.
Учитель математики:
– Здравствуйте, ребята!
– Сегодня у нас урок-закрепление по теме: “Дроби и ноты”.
– Он у нас необычный. Мы будем заниматься математикой и музыкой.
Музыка: Математика и Музыка – два школьных предмета, два полюса человеческой культуры. Слушая музыку, мы попадаем в волшебный мир звуков. Решая задачи, погружаемся в строгое пространство чисел. И не задумываемся о том, что мир звуков и пространство чисел издавна соседствуют друг с другом. Более того, они тесно взаимосвязаны внутренне.
Математика: Именно исследованию музыки математическими средствами посвящали свои работы величайшие математики: Рене Декарт, Готфрид Лейбниц, Леонард Эйлер, Христиан Гольдбах, Даниил Бернулли.
Первая крупная работа Леонарда Эйлера – «Диссертация о звуке», созданная в 1727 году, начиналась словами: «Моей конечной целью в этом труде было то, что я стремился представить музыку как часть математики и вывести в надлежащем порядке всё, что может сделать приятным объединение и смешивание звуков»
Лейбниц в письме Гольдбаху пишет: «Музыка есть бессознательное арифметическое упражнение души, не умеющей считать».
На этом уроке мы должны закрепить знания об обыкновенных дробях: сложение и вычитание дробей с одинаковыми и разными знаменателями, сравнение дробей.
Учитель музыки: Закрепить видение нот как своеобразной знаковой формы дробей.
2. Повторение.
Мы живем в мире звуков. Люди давно научились записывать различные звуки с помощью специальных знаков. Звуки человеческой речи, например, записываются с помощью букв, а музыкальные звуки записываются с помощью нот.
Учитель музыки:
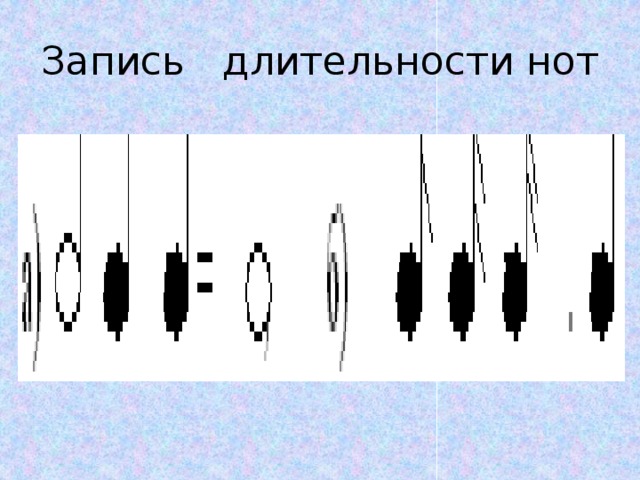
– На уроках музыки мы изучали ноты, длительность звучания. Так вот ноты отличаются по длительности их звучания. Самая “длинная” нота – целая. Ее обозначают знаком 
. С точки зрения математики целую ноту можно принять за единицу (1). Давайте послушаем, как долго звучит эта нота (звучит цельная нота).
– Запишем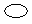 
– целая 1.
– Нота вдвое короче называется половинной и обозначается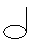 
.
Послушаем длительность звучания половинной ноты (звучит половинная нота). Какая же дробь соответствует половинной ноте? Половинной ноте соответствует дробь 1/2.
– Запишем 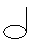– половинная 1/2.
– Послушаем ноту, которая еще в два раза короче (звучит нота). Это четвертная.
– Запишем 
– четвертная 1/4.
– Восьмая нота имеет еще меньшую длительность. Слушаем (звучит нота).
– Запишем 
– восьмая 1/8.
– И, наконец, самая короткая нота шестнадцатая (звучит нота).
– Запишем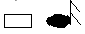 
– шестнадцатая 1/16.
3. Закрепление.
Учитель математики:
– Ребята, обратимся к опорной схеме “Дроби и ноты”.
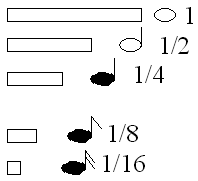
– Какая же нота имеет наименьшую длительность?
– А какая наибольшую длительность?
– Хорошо, молодцы!
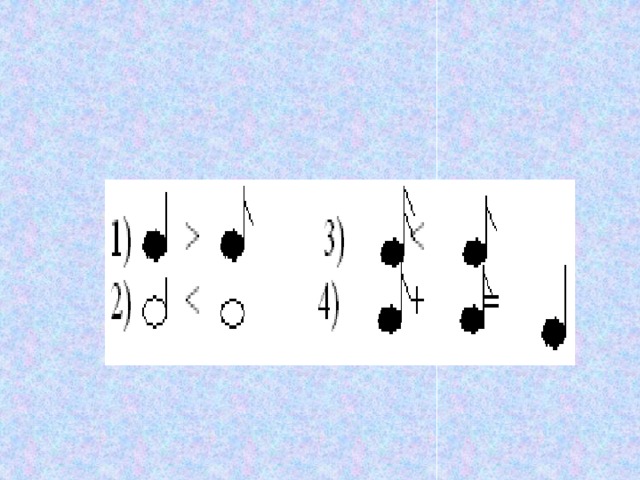
– Ребята! Сравним длительности звучания таких нот.
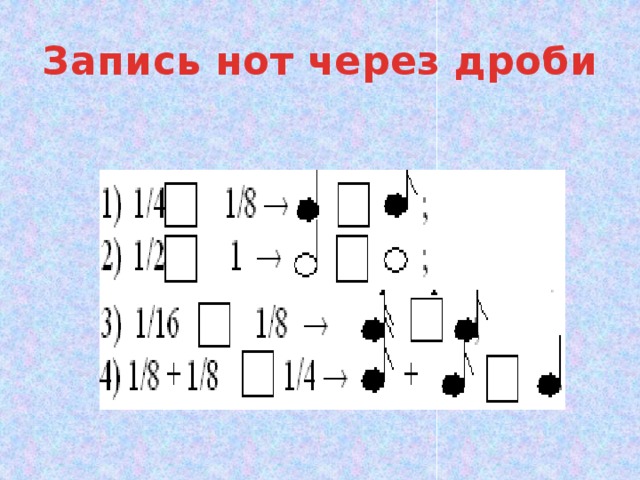
Для того чтобы выполнить это задание запишем ноты через дроби. Итак, сравним.
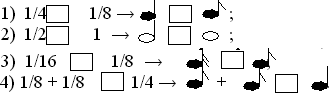
На карточке №1 вы видите эти дроби, вам необходимо поставить знаки или =, соответственно сравнить длительность звучания данных нот.
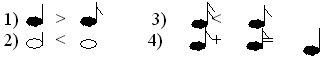
Сформулируйте правило, которое использовали при сравнении этих дробей (из двух дробей с равным числителем больше та, у которой знаменатель меньше). Проверьте друг друга и поставьте оценки.
Но в музыке не используется знак “+”, поэтому равенства длительностей нот лучше записывать так:
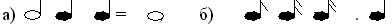
Проверим эти равенства на доске.
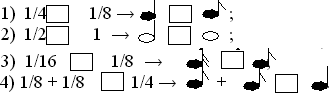
а) 1/2 + 1/4 + 1/4 = 2/4 + 2/4 = 4/4 = 1;
б) 1/8 + 1/16 + 1/16 = 1/8 + 2/16 = 1/8 + 1/8 = 2/8 = 1/4.
В приведенных равенствах одной ноты не хватает:
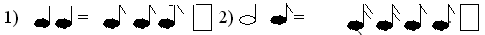
Найдите недостающую ноту (самостоятельно):
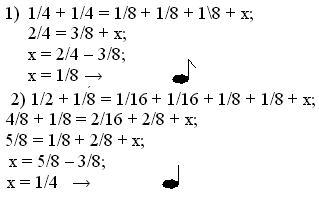
Учитель музыки:
Посмотрим теперь на нотный стан, изображенный на доске и на раздаточных карточках.
Из рисунка мы видим, что нотная запись разбита вертикальными линиями на отдельные части: каждая такая часть называется тактом.
Учитель математики:
Посчитаем общую длительность всех нот, входящих в каждый такт (все ответы запишем в виде дроби со знаменателем 4):
1/8 + 1/8 + 1/8 + 1/8 = 4/8 = 2/4;
1/4 + 1/8 + 1/8 = 1/4 + 2/8 1/4 + 1/4 = 2/4;
1/4 + 1/4 = 2/4;
1/8 + 1/8 + 1/8 + 1/8 = 4/8 = 2/4;
1/8 + 1/8 + 1/8 + 1/8 = 4/8 = 2/4.
Как видим, в каждом случае мы получили одно и то же число 2/4. Это число называется размером музыкального произведения и записывается в начале нотного стана.
Теперь послушаем это произведение, с нотной записью которого мы работали. Угадайте название этой песни.
(Русская народная песня “Во поле береза стояла”).
На карточке записана мелодия без разбиения на такты. Сделайте самостоятельно, зная размер произведения – 2/4.
1/8 + 1/8 = 2/8 = 1/4 + 1/8 = 2/8 + 1/8 = 3/8 + 1/8 = 4/8 = 2/4;
1/4 + 1/4 = 2/4;
1/8 + 1/8 + 1/8 + 1/8 = 2/4;
1/4 + 1/4 = 2/4;
1/4 + 1/8 + 1/8 = 1/4 + 2/8 = 1/4 + 1/4 = 2/4;
1/4 + 1/8 + 1/8 = 2/4;
1/8 + 1/8 + 1/4 = 2/4;
1/4 + 1/4 = 2/4.
Послушаем эту мелодию и угадаем название песни.
(Белорусская народная песня “Перепелочка”).
И последнее задание тест-обобщение “Дроби”.
1. Какие из высказываний относительно дробей 1/2, 1/4, 1/8, 1/16 неверны?
а) Числители всех дробей равны 1.
б) Знаменатели являются четными числами.
в) Дроби соответствуют длительности звучания разных нот.
г) Эти дроби нельзя сравнить.
2. Какая из этих дробей является наибольшей?
а) 1/4; б) 1/2; в) 1/8; г) 1/16.
3. Какая из этих дробей является наименьшей?
А) 1/4; б) 1/16; в) 1/2; г) 1/8.
4. В каком порядке расположены дроби 1/16, 1/8, 1/4, 1/2?
а) Возрастания.
б) Убывания.
4. Подведение итогов урока.
Ну что, ребята, наша работа подошла к концу.
Карточки вложите в тетради и передайте мне.
Оценки за устные ответы.
Домашнее задание Ребята, что же мы узнали на уроке?
Вообще, нужны ли нам дроби?
Исполним песню “О дробях”.
О дробях.
(На мотив песни “Чему учат в школе”).
Дроби всякие нужны,
Дроби разные важны.
Дробь учи, тогда сверкнет тебе удача.
Если будешь дроби знать,
Точно смысл понимать,
Станет легкой даже трудная задача.
Дробь свою “переверни”, (это слово обсуждаем)
Повнимательней взгляни.
Вдруг из правильной неправильную видишь.
Эти дроби перемножь,
Единицу ты найдешь,
Их обратными зови и не обидишь.
Дробь на дробь чтоб разделить,
Долго нечего мудрить.
Дробь обратную делителю берете.
И на эту дробь теперь
Умножайте поскорей,
Так искомое вы частное найдете.
Спасибо, ребята, за работу на уроке. Спасибо гостям!
1. Какие из высказываний относительно дробей 1/2, 1/4, 1/8, 1/16 неверны?
а) Числители всех дробей равны 1.
б) Знаменатели являются четными числами.
в) Дроби соответствуют длительности звучания разных нот.
г) Эти дроби нельзя сравнить.
2. Какая из этих дробей является наибольшей?
а) 1/4; б) 1/2; в) 1/8; г) 1/16.
3. Какая из этих дробей является наименьшей?
А) 1/4; б) 1/16; в) 1/2; г) 1/8.
4. В каком порядке расположены дроби 1/16, 1/8, 1/4, 1/2?
а) Возрастания.
б) Убывания.
1. Какие из высказываний относительно дробей 1/2, 1/4, 1/8, 1/16 неверны?
а) Числители всех дробей равны 1.
б) Знаменатели являются четными числами.
в) Дроби соответствуют длительности звучания разных нот.
г) Эти дроби нельзя сравнить.
2. Какая из этих дробей является наибольшей?
а) 1/4; б) 1/2; в) 1/8; г) 1/16.
3. Какая из этих дробей является наименьшей?
А) 1/4; б) 1/16; в) 1/2; г) 1/8.
4. В каком порядке расположены дроби 1/16, 1/8, 1/4, 1/2?
а) Возрастания.
б) Убывания.
1. Какие из высказываний относительно дробей 1/2, 1/4, 1/8, 1/16 неверны?
а) Числители всех дробей равны 1.
б) Знаменатели являются четными числами.
в) Дроби соответствуют длительности звучания разных нот.
г) Эти дроби нельзя сравнить.
2. Какая из этих дробей является наибольшей?
а) 1/4; б) 1/2; в) 1/8; г) 1/16.
3. Какая из этих дробей является наименьшей?
А) 1/4; б) 1/16; в) 1/2; г) 1/8.
4. В каком порядке расположены дроби 1/16, 1/8, 1/4, 1/2?
а) Возрастания.
б) Убывания.
Можно бесконечно и многогранно говорить об исторической взаимосвязи наших предметов. Но, и перемахнув в современность, можно найти немало интересных точек соприкосновения математики и музыкального ритма.
Не слышали о таких?
То, что музыка и стихи неразделимы в песнях, понимает каждый. А как цифры могут быть связаны со стихотворчеством.
Одним из примет нынешнего века является необходимость оцифровывать любую информацию. Звуки и картинки почти полностью перебрались «в цифру», но это как-то до поры до времени обходило стороной поэзию, а зря. Цифровые стихи обладают особым обаянием, ритмом и своеобразной энергетикой. Их обязательно надо читать с выражением и вслух, иначе ничего не поймете — цифровые стихи ближе к музыке, ведь ни там, ни там нет слов и готовых образов.
Они зародились в 2000 году и их поначалу называли «дигитальными стихами» или «авральным стихотворчеством». Их можно отнести скорее к математическим и литературным развлечениям. Но кто с ними уже встречался, называет это чудом. По своей информативности, эмоциональной насыщенности, динамике и образности цифровые стихи ближе к музыке — ведь в музыке тоже нет слов и готовых образов, но она красива и волнительна. Для тех, кто еще сомневается, привожу пример. Числа здесь и далее разделены пробелами. Соберитесь, сосредоточьтесь и продекламируйте нараспев:
128 49
138 45
13 30 29
12 8 35
Ну как? Почувствовали ритм? Попробуйте сами сочинить — получите огромное удовольствие от приобщения к поэзии цифр через цифровую поэзию. Для тех, кто не попал под обаяние ритма и ждущих практической отдачи, можно сообщить, что цифровая поэзия служит идеальным средством обучению теории стихосложения.
А для начала попробуем напеть уже готовые цифровые стихи на хорошо известные вам мелодии.
Антошка, Антошка…
первый куплет.
13,12,
120 30 40,
13, 12,
120 30 8 0.
припев.
3 16,
8 20,
18 40 20
35 12 10…
Жили у бабуси…
40 38
2 128
1 10 1 10
2 128
Гимн России
16 13
12 4
17 15 14 2
13 16
4 12
15 14 132!
А в заключение этого раздела - задание посложнее:
Попробуйте угадать, какой фрагмент из творчества Александра Сергеевича Пушкина выражен цифровым стихом.
Пушкин
17 30 48
140 10 01
126 138
140 3 501
