Знать определения линейного уравнения, родственных уравнений с одной переменной

Ұзақ мерзімді жоспар бөлімі: 6.3А Бір айнымалысы бар сызықтық теңдеу

Мектеп: «Манашы орта мектебі» КММ

Күні: 16.01.2019ж

Мұғалімнің аты-жөні: Самаликова Р.Н.

Сынып: 6

Қатысқандар саны:

Қатыспағандар:

Сабақ тақырыбы:

Бір айнымалысы бар сызықтық теңдеу

Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме)

6.2.2.2

бір айнымалысы бар сызықтық теңдеудің, мәндес теңдеулердің анықтамаларын білу;

6.2.2.3

бір айнымалысы бар сызықтық теңдеулерді шешу.

Сабақ мақсаты:

Бір айнымалысы бар сызықтық теңдеудің, мәндес теңдеулердің анықтамаларын біледі. Бір айнымалысы бар сызықтық теңдеулерді шешеді.

Бағалау критерийі

Оқушылар осы тақырып бойынша білу, түсіну, талдау, қолдану, анализ, синтез, ойлау дағдыларын қалыптастыруы тиіс.

Тілдік мақсаттар

Осы тақырыпқа қатысты терминдерді үш тілде меңгереді, қазақ, орыс, ағылшын тіліндегі әдебиеттердегі материалдарды меңгере алады. Ол үшін мынадай сөздіктер қолданамын:

Құндылықтарға баулу

• жұппен жұмыс жасай отырып оқушыларды өзара сыйластыққа, сенімділікке баулу;

• оқушы өз бетімен ақпаратты табу;

• қарым-қатынас орнатуда сыни тұрғыдан ойлану.

Пәнаралық байланыс

Геометрия, тарих, география.

Алдыңғы білім

Санды теңдіктер және олардың қасиеттері.

Сабақ барысы

Сабақтың жоспарланған кезеңдері

Сабақтағы жоспарланған жаттығу түрлері

Ресурстар

Сабақтың басы

І. Ұйымдастыру

1) Сәлемдесу;

2) Оқушыларды түгелдеу;

3) Оқушылардың назарын сабаққа аудару;

4) Топқа бөлу.

Сабақтың ортасы

ІІ. Үй тапсырмасын тексеру: Тура санды теңдіктердің қасиеттерін сәйкестендіру.

Егер а=b, b=c болса, онда a=c

1-қасиеті

Егер тура санды теңдіктердің оң жақ және сол жақ бөліктерін жеке-жеке көбейтсе, онда тура санды теңдік шығады, яғни а=b, және с=d болса, онда ac=bd

2-қасиеті

3-қасиеті

Егер тура теңдіктің екі жақ бөлігіне бірдей санды қосса, онда тура санды теңдік шығады, яғни а=b болса, онда a+с=b+c

4-қасиеті

Егер тура санды теңдіктердің оң жақ және сол жақ бөліктерін жеке—жеке қосса, онда тура санды теңдік шығады, яғни a=b және c=d болса, онда a+c=b+d

5-қасиеті

Егер тура санды теңдіктің екі жақ бөлігін бірдей санға көбейтсек немесе нөлге тең емес бірдеей санға бөлсек, онда тура санды теңдік шығады, яғни a=b болса, онда ac=bc немесе

ІІІ. Ой қозғау:

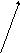
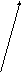
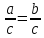
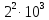1. Алтын адам киімі алтын әшекеймен безендірілген. Олардың саны көбейтіндісінің мәніне тең. Алтын адамның киімінде қанша алтын әшекей бар?

(4000)

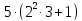1. Алтын адамның бас киімінің биіктігі сантиметрмен алынған өрнегінің мәніне тең. Бас киімнің биіктігін табыңдар.

(65см)

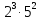1. Бас киім саны өрнегінің мәнінен артық және ол барыстың, арқардың, тауешкінің, жылқының, құстың бейнелері салынған алтын заттармен әшекейленген. Бас киімде қанша алтын зат бар?

(200ден астам)

ІV. Жаңа тақырыпты ашу:

aх=b (мұндағы х – айнымалы, а және b – қандай да бір сандар) түріндегі теңдеу бір айнымалысы бар сызықтық теңдеу деп аталады.

aх=b сызықтық теңдеуіндегі х белгісіз көбейткішті табу үшін көбейтіндінің мәні b-ны белгілі көбейткіш а-ға бөлу керек.

Мысалы: 2х + 4 = 6

2х = 6 – 4

2х = 2

х = 1 Жауабы: 1

Түбірлері бірдей болатын немесе түбірлері болмайтын теңдеулер мәндес теңдеулер деп аталады.

Мысалы: Неліктен х + 8 = 18 және х + 8 – 6х = 18 – 6х теңдеулері мәндес болады?

Тексеру: х + 8 = 18 х + 8 – 6х = 18 – 6х

х = 18 – 8 х – 6х + 6х = 18 – 8

х = 10 х = 10 Жауабы: 10

Екі теңдеудің де мәні 10 санына тең болатынына көз жеткіздік. Демек, мұндай теңдеулер мәндес теңдеулер деп аталады.

Егер теңдеудің түбірі (шешімі) болмаса, онда шешімдер жиынын бос жиын деп атайды. Бос жиын таңбасымен белгіленеді.

Мысалы: -5х – 0,74 = -5х + 0,26 теңдеуін шешейік.

Шешуі: -5х – 0,74 = -5х + 0,26

-5х + 5х = 0,26 + 0,74

0 · х = 1

Мұндай теңдеудің түбірі болмайды. Демек, теңдеудің шешімі бос жиын.

V. Сыныппен жұмыс. Есептер шығару

Топтық жұмыс №837

Берілген теңдеулерді шешіп, әлемнің 7 кереметі туралы мағлұмат алыңдар:

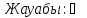
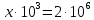1. теңдеуінің түбірі – біздің заманымызға дейінгі Мысыр пирамидалары салынған жыл:

Жауабы: б.з.д 2000ж

1. 1000 – х = 570 теңдеуінің түбірі – біздің заманымызға дейінгі Галикарнастағы Мавзолей салынған жыл:

Жауабы: б.з.д 430ж

1. 99х = 693 теңдеуінің түбірі - біздің заманымызға дейінгі Эфестегі Артемида храмы салынған ғасыр:

Жауабы: б.з.д 7ғ

1. 8280 : х = 2070 теңдеуінің түбірі - біздің заманымызға дейінгі Олимп тауындағы Зевс мүсіні салынған ғасыр:

Жауабы: б.з.д 4ғ

1. х + 450 = 1000 теңдеуінің түбірі - біздің заманымызға дейінгі Вавилондағы Семирамида аспалы бағы салынған жыл:

Жауабы: б.з.д 550ж

1. х : 73 = 4 теңдеуінің түбірі - біздің заманымызға дейінгі Родостағы Гелиос мүсіні салынған жыл:

Жауабы: б.з.д 292ж

1. х – 188 = 92 теңдеуінің түбірі – біздің заманымызға дейінгі Мысырдағы Александрия маягі салынған жыл:

Жауабы: б.з.д 280ж

Жұппен жұмыс №849

Берілген теңдеулерді шешіп, Шығыс Қазақстан облысында орналасқан Марқакөл қорығы туралы мағлұматтар алыңдар:

а) х + 0,24 = 20 + 0,99х теңдеудің түбірі – қорықтың құрылған жылы:

Жауабы: 1976ж

ә) 3у – 2(169,9 + у) = 150 – (у + 339,8) теңдеуінің түбірі – қорықтық ауданының (мың гектар) өлшемі:

Жауабы: 75мың га

б) 50z + (z + 6,2) = 200 теңдеуінің түбірі – қорықтағы орманның ауданының (мың гектар) өлшемі:

Жауабы: 3,8мың га

Жеке жұмыс №844

1. 40 + 2х = 3x – 15

1. 95y – 4,9 = 98y – 1

VII. Сергіту сәті. «Миға шабуыл»

1. Суретке сәйкес теңдеуді тап:

х + 6 = 10

Теңдеуді шеш:

x – 6 = 10

х = +

x – 6 = 10 + x

х =

Жауабы: 16

1. Кәмшат Гауһардан 3 жас кіші. Екеуінің жастарының қосындысы 29-ға тең. Әрқайсысының жасын тап.

х + х - =

х = 29 +

х = 32

16

13

х = Кәмшат жаста, Гауһар жаста.

1. Бос орындарды толтыр:

(3х + 4) : 2 =11

3х + 4 = ·

3х + 4 =

3х = -

3х =

х =

х = Жауабы: 6

1. – 2х = 24 теңдеуінің түбірін тап:

а) 12

б) -16

в) 1

г) – 12 Жауабы: - 12

Bilimland сайты, 6-сынып

Сабақтың соңы

Рефлексия және үй тапсырмасын беру

Үйге тапсырма: §29. № 844(2, 3)

Рефлексия: Білемін...

Білдім...

Білгім келеді...