"Значение тригонометрических функций"-геометрия 8 класс

Тема: Значения тригонометрических функций синуса, косинуса, тангенса и котангенса углов треугольника/1/.

Цели урока: 

-образовательные – ввести понятие синус, косинус, тангенс угла от 0° до 180°. Вывести основное тригонометрическое тождество и формулы для вычисления координат точки. Рассмотреть формулы приведения.

-развивающие – формирование понятия о синусе, косинусе, тангенсе как функциях от угла, области определения тригонометрических функций, развитие логического мышления, развитие правильной математической речи;

-воспитательные – развитие навыка самостоятельной работы, культуры поведения, аккуратности в ведении записей.

Ход урок:

1. Организационный момент. 
«Образование – это не количество прослушанных уроков, а количество понятых. Так что, если хотите идти вперед, то поспешайте медленно и будьте внимательны»

2. Мотивация урока.
    Один мудрец сказал: « Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – это треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но возвысите свою душу».
    Мы вместе с вами попробуем провести небольшое исследование. Давайте делиться своими идеями, которые придут вам в голову, и не бойтесь ошибиться, любая мысль может дать нам новое направление поиска. Пусть наши достижения и не покажутся кому-то крупными, но ведь это будут наши собственные достижения!

3.Устный опрос:

-Какие могут быть углы? 

-Как называются стороны прямоугольного треугольника? 

-Что такое катет?

-Что такое гипотенуза?
-Какие соотношения между сторонами и углами этого треугольника вы знаете? 

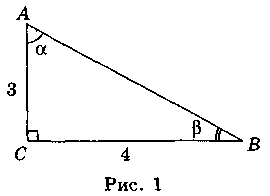
-Найти по рис. 1 sinα, cosα, tgα, cosβ, sinβ, tgβ.

4. Изучение нового материала.
В древности люди следили за светилами и по этим наблюдениям вели календарь, рассчитывали сроки сева, время разлива рек; корабли на море, караваны на суше ориентировались в пути по звездам. Все это привело к потребности научиться вычислять стороны в треугольнике, две вершины которого находятся на земле, а третья представляется точкой на звездном небе. Исходя из этой потребности и возникла наука – тригонометрия – наука, изучающая связи между сторонами в треугольнике.

    Как вы думаете, достаточно ли уже известных нам соотношений для решения таких задач?
    Цель сегодняшнего урока – исследовать новые связи и зависимости, вывести соотношения, применяя которые на следующих уроках геометрии, вы сможете такие задачи решать.
    Давайте почувствуем себя в роли научных работников и вслед за гениями древности Фалесом, Евклидом, Пифагором пройдем путь поиска истины.
    До сих пор значения синуса, косинуса и тангенса были определены только для острых углов. Теперь мы определим их для любого угла от 0° до 180°. 

sinα =  = = у; cosα =  =  = x; tgα =  = ;
 

Пользуясь данным определением, для любого угла α, 0° < α < 180°:
sin 0° = 0, cos 0° = 1, tg 0° = 0; sin 180° = 0, cos 180° = -l, tg 180° = 0.
Sin(90°- α)= cos α, cos (90°- α)= Sin α. 
 

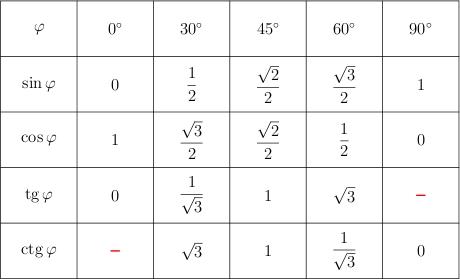
Таблица значений синуса, косинуса, тангенса и котангенса для «хороших» углов от  до .

Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.

 5. Закрепление нового материала: №150/1/,151,152,154,155/1/,157/1/.

6.Домашнее задание: №150/2/,153,155/2/,156.

7.Итоги урока.

?ых сторон 4 см. Чему равен периметр этой трапеции? (10 см)

6.Домашнее задание: №165,166,167.

7.Итоги урока.

ont-family:"Times New Roman"'>