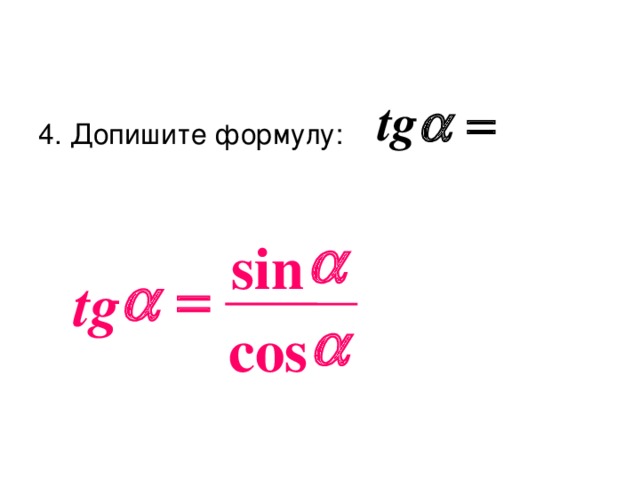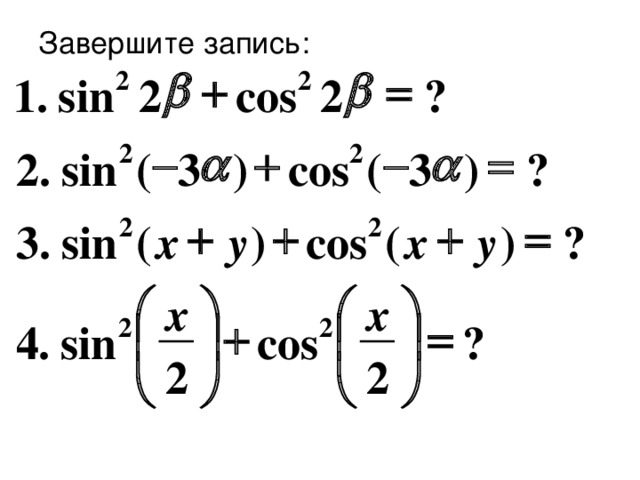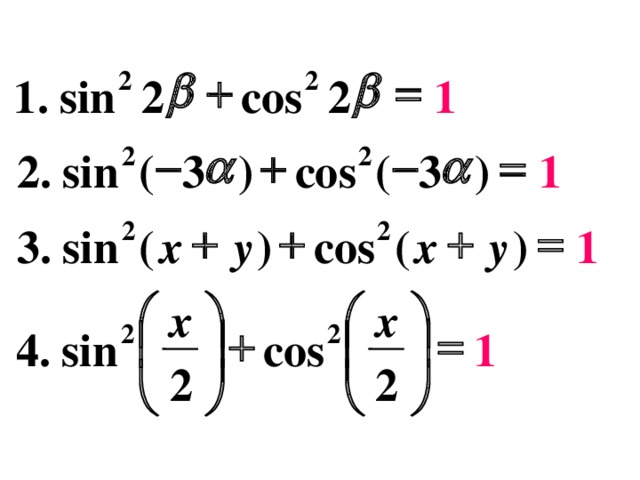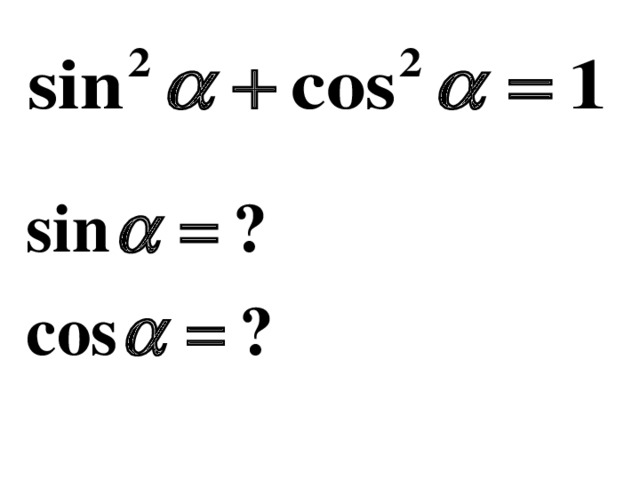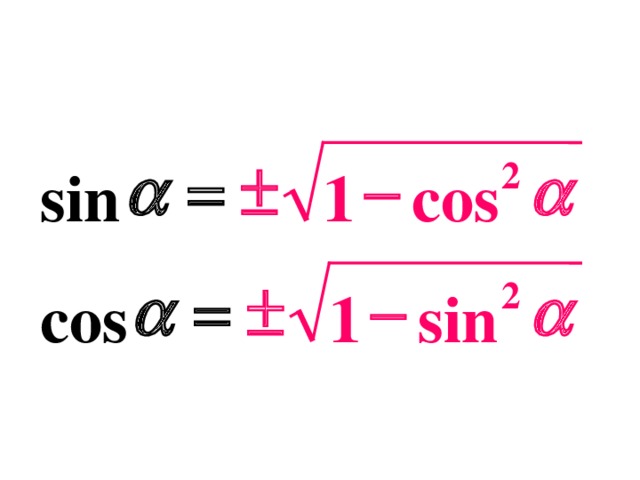Зависимость между синусом, косинусом и тангенсом одного и того же угла

КАРТА УРОКА «ЗАВИСИМОСТЬ МЕЖДУ СИНУСОМ, КОСИНУСОМ И ТАНГЕНСОМ ОДНОГО И ТОГО ЖЕ УГЛА»

Учащийся _______________________________________________________________________

Мои баллы: __________

Максимальное кол-во баллов – 22

18 – 22 балла — оценка «5»

15 – 17 баллов — оценка «4»

11 –14 баллов — оценка «3»

Менее 11 баллов — нужно прийти на консультацию в ближайшие дни, материал еще не усвоился.

Головатова Вера Анатольевна, преподаватель математики

ГБ ПОУ «Охтинский колледж»

Конспект двух уроков для обучающихся I курса (10кл.) по теме:

«Зависимость между синусом, косинусом и тангенсом одного и того же угла»

Цель: изучить зависимость между синусом, косинусом и тангенсом одного и того же угла.

Для достижения поставленной цели необходимо:

1. Знать:

1. формулировки определений основных тригонометрических функций (синуса, косинуса и тангенса);

2. знаки тригонометрических функций по четвертям;

3. множество значений тригонометрических функций;

4. основные формулы тригонометрии.

1. Понимать:

1. что пользоваться основным тригонометрическим тождеством можно только для одного и того же аргумента;

2. алгоритм вычисления одной тригонометрической функции через другую.

1. Применить:

1. умение правильно выбрать нужную формулу для решения конкретного задания;

2. умение работать с простыми дробями;

3. умение выполнять преобразование тригонометрических выражений.

1. Анализ:

1. анализировать ошибки в логике рассуждения.

1. Синтез:

1. предложить свой способ решения примеров;

2. составить кроссворд, используя полученные знания.

1. Оценка:

1. знаний и умений по данной теме для использования в других разделах алгебры.

Оборудование: макет тригонометрической окружности, раздаточный справочный материал с формулами и таблицами значений тригонометрических функций, компьютер, мультимедийный проектор, презентация, листы с заданиями для самостоятельной работы.

Используемые источники:

1. Алгебра и начала анализа: Учебник для 10-11 кл. общеобразоват. учреждений / Ш.А.Алимов, Ю.В. Сидоров и др. Просвещение, 2006.

2. Задания Открытого банка для подготовки к ЕГЭ по математике, 2011 г.

3. Ресурсы сети ИНТЕРНЕТ.

Краткий план урока:

1. Организационный момент.

Приветствие. Сообщение цели урока и плана работы на уроке – 3-5 мин.

1. Актуализация знаний и умений.

Учащимся раздаются карты урока и даются пояснения как с ними работать.

На экран выводятся вопросы; учащиеся записывают ответы в тетрадь; преподаватель выводит на экран правильный ответ. После окончания опроса учащиеся выставляют баллы в карту урока для Задания № 1 – 10 мин.

1. Объяснение нового материала.

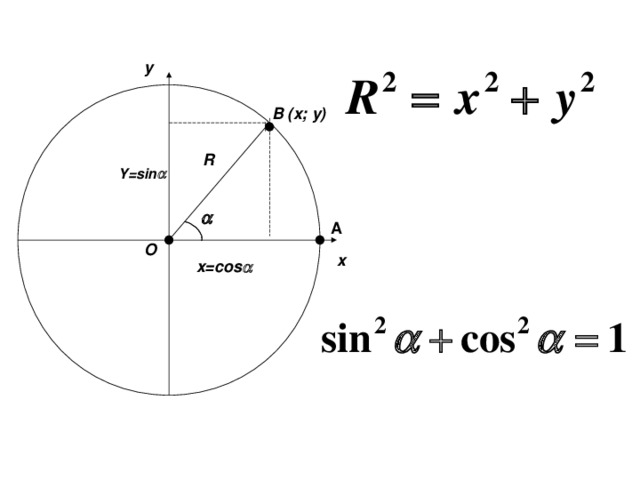
1. Преподаватель выводит формулу для основного тригонометрического тождества – 5 мин.

2. Учащимся предлагается самостоятельно завершить запись примеров, выведенных на экран, проверить правильность ответов и выставить баллы в карту урока для Задания № 2 – 5 мин.

3. Учащимся в тетради предлагается самостоятельно выразить из основного тригонометрического тождества синус через косинус и косинус через синус. На экран выводится правильный ответ, учащиеся проверяют и выставляют баллы в карту урока для Задания №3 – 5-7 мин.

4. Преподаватель на доске решает примеры на применение основного тригонометрического тождества. Учащиеся отвечают на вопросы преподавателя по ходу объяснения и записывают примеры себе в тетрадь – 15 мин.

5. Преподаватель выводит формулы, показывающие зависимость между тангенсом и котангенсом, учащиеся принимают активное участие в выводе формул, отвечают на вопросы и делают записи в тетрадь – 5 мин.

6. Преподаватель выводит формулы, показывающие зависимость между тангенсом и косинусом, между синусом и котангенсом – 5 мин.

7. К доске вызываются учащиеся по желанию и с помощью преподавателя по алгоритму выполняют решение примеров. Все остальные записывают и по мере необходимости отвечают на вопросы – 10 мин.

1. Закрепление изученного материала

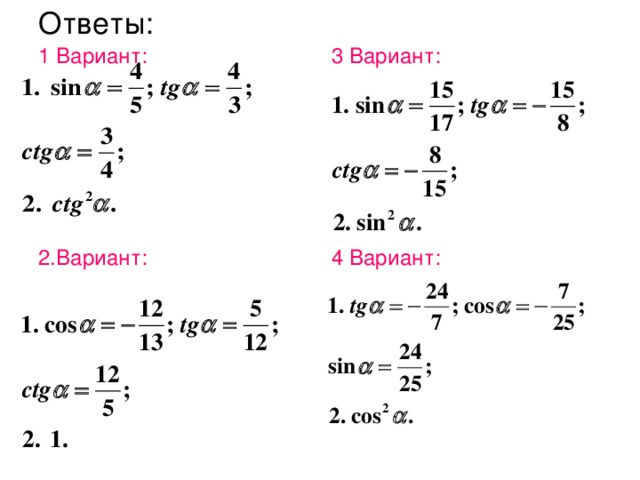
На экран выводятся рубрики самооценки. Каждому выдается лист с заданиями. Учащиеся самостоятельно решают задания на применение выведенных формул. Номер варианта соответствует рубрикам самооценки.

В конце урока на экран выводятся правильные ответы, учащиеся проверяют свои ответы и выставляют баллы в карту урока для Задания № 4 – 20 мин.

1. Домашнее задание: Учащиеся записывают в тетрадь задание на дом – 3 мин.

После посещения семинаров по РНС и проведении урока с использованием технологической карты мне стало очевидно, что рейтинговая система стимулирует максимально возможный интерес учащихся к конкретной теме. В моем случае – это основные формулы тригонометрии.

Тригонометрия очень часто не воспринимается учащимися не столько из-за своей сложности, сколько из-за большого количества формул, с которыми нужно уметь работать.

Трудно после одного урока, проведенного с использованием технологической карты, ожидать каких-то невероятных успехов и результатов, но мне кажется, что преимущества рейтинговой системы при изучении тригонометрии и математики в целом состоят в следующем:

• появилась возможность организовать и поддерживать как работу на уроке, так и самостоятельную, систематическую работу учащихся дома;

• должна повыситься посещаемость и уровень дисциплины на уроках;

• повышается мотивация к учебной деятельности;

• уменьшаются стрессовые ситуации при получении неудовлетворительных оценок;

• стимулируется творческое отношение к работе.

Единственный недостаток РНС (как мне кажется) – это большой объем работы для преподавателя, но это работа на результат. После единственного урока, проведенного по этой системе, учащиеся постоянно спрашивают, будем ли мы еще так работать. Значит, их что-то зацепило. И нужно продолжать работать.

САМОСТОЯТЕЛЬНАЯ РАБОТА

РУБРИКИ САМООЦЕНКИ:

1. Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, но с помощью наводящих вопросов (карточка – инструкция).

2. Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, используя указания преподавателя.

3. + Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, без наводящих вопросов и указаний.

4. + Я понял тему и могу решать примеры по алгоритму, не заглядывая в тетрадь.

Какой бы уровень вы не выбрали, сначала внимательно просмотрите все задания, которые я вам раздала, а затем выполните задание, соответствующее выбранному вами уровню (перед вами задания четырех вариантов, номер варианта соответствует уровням самооценки.)

1 вариант

1. Дано: Найдите

Инструкция:

• определите четверть, в которой находится угол . Если возникают затруднения, то можно посмотреть в справочнике;

• определите знак функции синус в этой четверти. Проверьте себя, посмотрев в справочник;

• напишите формулу (2) из сегодняшнего урока, указав перед корнем знак, который выбрали ранее;

• в написанное выражение подставьте значение косинуса, вспомните, как дробь возводится в квадрат (нужно возвести в квадрат числитель и знаменатель дроби);

• выполните вычисления под корнем, извлеките корень (нужно извлечь корень из числителя и знаменателя);

• вспомните определение функции тангенс, (можно посмотреть в справочник), запишите формулу;

• правильно выполните деление дробей: при делении дроби на дробь, вторую дробь нужно перевернуть и дальше числитель первой дроби умножить на числитель получившейся дроби, тоже нужно сделать и со знаменателями: ;

• функцию котангенс можно найти по формуле (6) из сегодняшнего урока;

• запишите ответ.

1. Упростите выражение:

Инструкция:

1. замените единицу равным ей выражением Только не забудьте, что в примере перед единицей стоит знак минус, значит у всех слагаемых изменится знак;

2. приведите подобные;

3. запишите ответ.

Решите самостоятельно этим способом пример:

2 вариант

1. Дано: Найдите

Указание: Для определения функции косинус воспользуйтесь формулой (3) из сегодняшнего урока. Не забудьте определить знак, который будет стоять перед корнем. Для вычисления значений тангенса и котангенса можно воспользоваться определением этих функций ил использовать формулы, которые мы вывели сегодня на уроке.

1. Упростите

Указание. Сгруппируйте первый и третий члены выражения, вынесите за скобку общий множитель….

3 вариант

1. Дано: Найдите

2. Упростите выражение: .

4 вариант

1. Дано: Найдите

2. Упростите выражение: .

Головатова Вера Анатольевна, преподаватель математики СПб ГБ ПОУ «Охтинский колледж»

Повторение:

1. В какой четверти находится угол в

1 радиан и чему он примерно равен?

В I четверти, 1 рад.  57,3 °

2. Какое слово пропущено в определении функции синус?

Синусом угла  называется ………… точки единичной окружности.

ОРДИНАТА

3. Какое слово пропущено в определении функции косинус?

Косинусом угла  называется

………… точки единичной окружности.

АБСЦИССА

4. Допишите формулу:



sin





tg



cos

5. Определите знак произведения:















345

25

cos

132

sin

tg







6. Какое значение может принимать синус?













1

sin

1

1

sin

или

7. Вычислите:

2

1

1

















2

2

2

2

2

2

2

2

y

B (x; y)

R

Y=sin 





A

O

x

x=cos 

Завершите запись:









2

2

?

1

.

sin

2

cos

2













2

2

)

3

(

sin

.

2

(

3

)

?

cos









2

2

.

?

x

y

x

y

)

(

cos

)

(

sin

3









x

x





2

2









sin

cos

4

?

.

2

2

















2

2

1

1

.

sin

2

cos

2













2

2

)

3

(

sin

.

2

(

3

)

1

cos









2

2

.

1

x

y

x

y

)

(

cos

)

(

sin

3









x

x





2

2









sin

cos

4

1

.

2

2



















2

cos

sin

1











2

cos

1

sin

Рубрики самооценки

• Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, но с помощью наводящих вопросов (карточка – инструкция).
• Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, используя указания преподавателя.
• + Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, без наводящих вопросов и указаний.
• + Я понял тему и могу решать примеры по алгоритму, не заглядывая в тетрадь.

Ответы:

1 Вариант:

3 Вариант:

2.Вариант:

4 Вариант: