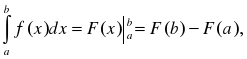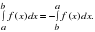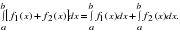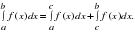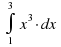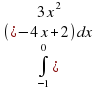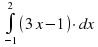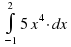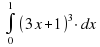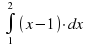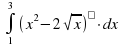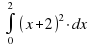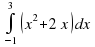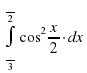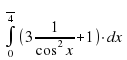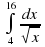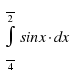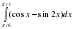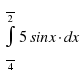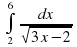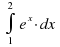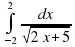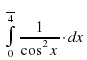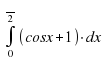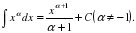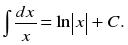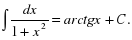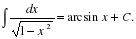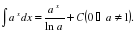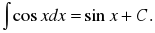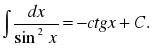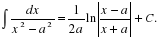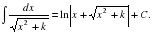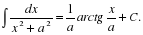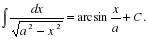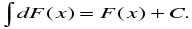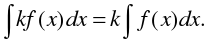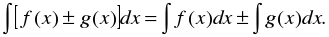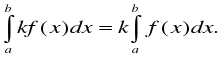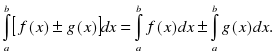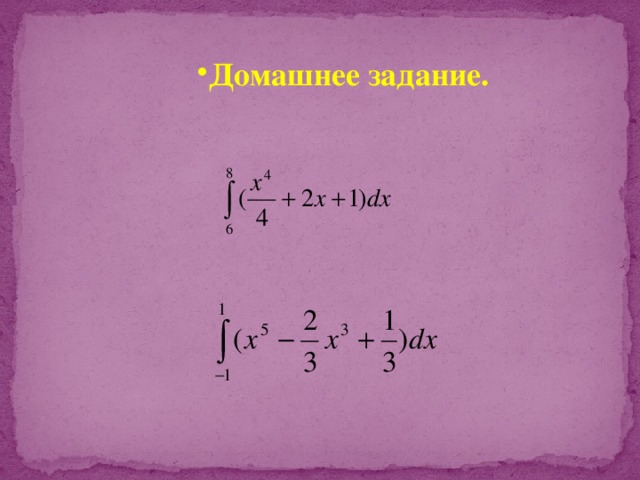Цель: : сформировать умения и навыки нахождения интегралов, используя простейшие правила интегрирования,таблицу первообразных.Научить вычислять интегралы в случаях, сводящихся к применению простейших правил интегрирования,таблицы первообразных.Развивать логическое мышление.Воспитывать интерес к предмету.
Тип урока: усвоение новых знаний.Метод урока: метод иллюстрации и демонстрации при устном изложении изучаемого материала, метод самостоятельной работы учащихся по осмыслению и усвоению нового материала, метод учебной работы по применению знаний на практике и выработке умений и навыков.
Просмотр содержимого документа
«2»
Просмотр содержимого документа
«Луганское высшее профессиональное училище»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИНАЛЬНОГО ОБРАЗОВАНИЯ ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ «ЛУГАНСКИЙ КОЛЛЕДЖ АВТОСЕРВИСА»
Разработка урока на тему:
«Определенный интеграл. Формула Ньютона-Лейбница»
Выполнила
Полтавская И.В.
Луганск - 2015
Цель: : сформировать умения и навыки нахождения интегралов, используя простейшие правила интегрирования ,таблицу первообразных.
Научить вычислять интегралы в случаях, сводящихся к применению простейших правил интегрирования ,таблицы первообразных.
Развивать логическое мышление.
Воспитывать интерес к предмету.
Тип урока: усвоение новых знаний
Метод урока: метод иллюстрации и демонстрации при устном изложении изучаемого материала, метод самостоятельной работы учащихся по осмыслению и усвоению нового материала, метод учебной работы по применению знаний на практике и выработке умений и навыков.
Структура урока.
Организационный момент – 1 мин.
Актуализация опорных знаний – 3 мин
Изучение нового материала – 7 мин.
Закрепление изученного материала – 32 мин.
Итог урока – 1,5 мин
Домашнее задание – 0,5 мин
Ход урока.
Организационный момент
Группа рассаживается по принципу: 1 ряд – учащиеся, чьи знания оцениваются на 9-12б; 2 ряд - учащиеся, чьи знания оцениваются на 6-8б; 3 ряд - учащиеся, чьи знания оцениваются на 1-5б.
Сообщается дата, тема урока и цель урока.
Актуализация опорных знаний
Актуализация проводится в виде фронтального опроса:
- определение неопределенного интеграла;
- основные свойства интеграла;
- как называется операция нахождения интеграла:
- как обозначается интеграл;
- какова отличительная особенность неопределенного интеграла.
Изучение нового материала.
Пусть 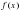 -функция, непрерывная на отрезке
-функция, непрерывная на отрезке 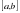 . Разобьем отрезок
. Разобьем отрезок 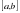
 на n-частичных(элементарных) отрезков
на n-частичных(элементарных) отрезков 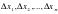 . В каждом из этих последовательных отрезков
. В каждом из этих последовательных отрезков 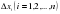 выберем точку
выберем точку 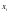 . Составим сумму вида
. Составим сумму вида
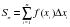 .
.  (1)
(1)
Эта сумма называется интегральной для функции 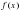 .
.
Определение . Определенным интегралом от данной функции 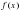 на данном промежутке
на данном промежутке 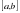 (или в пределах от a до b) называется предел соответствующей интегральной суммы при условии, что длина наибольшего элементарного отрезка подразбиения стремится к нулю, т.е.
(или в пределах от a до b) называется предел соответствующей интегральной суммы при условии, что длина наибольшего элементарного отрезка подразбиения стремится к нулю, т.е.
 . (2)
. (2)
Числа a и b называются соответственно нижним и верхним пределами интегрирования определенного интеграла (2). Заметим, что знак интеграла есть стилизованная сумма.
Формула Ньютона-Лейбница
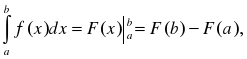
Свойства определенного интеграла
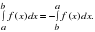

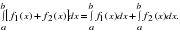
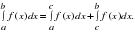
4. Закрепление изученного материала
На каждую парту кладутся задания, соответствующие их уровню. Первые у них задания одинаковые, поэтому для его решения выходит учащийся из 1-ой бригады. Далее 1-я бригада самостоятельно работает.
Доска делится на 2 половинки, на одной работает 2-я бригада, на другой – 3-я бригада.
Вычислить интеграл
|
| 1 | 2 | 3 |
| 1 | 
| 
| 
|
| 2 | 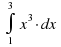
| 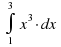
| 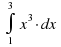
|
| 3 | 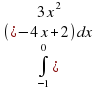
| 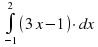
| 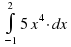
|
| 4 | 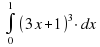
| 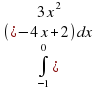
| 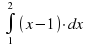
|
| 5 | 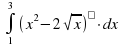
| 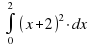
| 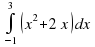
|
| 6 | 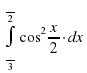
| 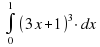
| 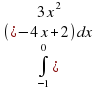
|
| 7 | 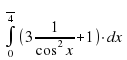
| 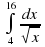
| 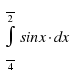
|
| 8 | 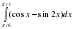
| 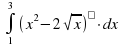
| 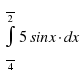
|
| 9 | 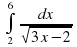
| 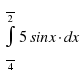
| 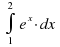
|
| 10 | 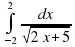
| 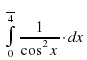
| 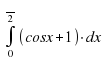
|
| 11 | 
| 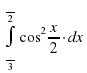
| 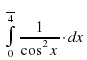
|
Итог урока – проводится оценивание работы учащихся.
Домашнее задание.


Просмотр содержимого документа
«Таблица основных интегралов»
Просмотр содержимого презентации
«Презентация1»
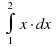
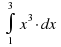

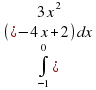
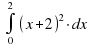
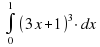
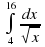
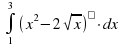
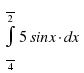
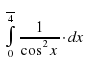
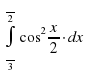
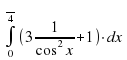
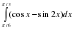
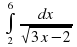
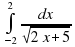
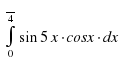

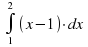
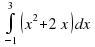
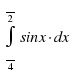
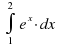

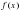 -функция, непрерывная на отрезке
-функция, непрерывная на отрезке 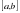 . Разобьем отрезок
. Разобьем отрезок  на n-частичных(элементарных) отрезков
на n-частичных(элементарных) отрезков 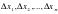 . В каждом из этих последовательных отрезков
. В каждом из этих последовательных отрезков 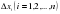 выберем точку
выберем точку 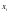 . Составим сумму вида
. Составим сумму вида 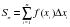 .
.  . (2)
. (2)