




 г. Армавир, 2005г.
г. Армавир, 2005г.
ЭПИГРФ К УРОКУ
Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три – четыре различные задачи. Решая одну задачу различными способами, можно путём сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.
Сойер У.
ЗАДАЧИ УРОКА:
- воспитательная задача: воспитание культуры поведения на уроке и стиля общения с учителем, одноклассниками;
- развивающая задача: развитие самостоятельности учащихся в обучении;
- обучающая задача: овладение методами (способами) решения систем уравнений, содержащих одно уравнение первой, другое второй степени.
ПЛАН УРОКА:
Устная работа.
Работа по карточкам.
Фронтальный опрос.
Задание на дом.
Работа в тетрадях (по группам).
Защита работ (по группам).
А ну-ка, разгадай!
Работа в тетрадях (индивидуальная).
Взаимоконтроль.
Самостоятельная работа по уровням.
11. Проверка самостоятельной работы.
12. Итог урока.
ОБОРУДОВАНИЕ УРОКА:
Мультимидийный проектор.
Презентация.
Компьютеры.
Тетради.
Доска.
Мел.
Цветные маркеры.
Половинки ватмана для защиты групповых работ.
Листики для выполнения самостоятельной работы.
Раздаточный материал для самостоятельной работы по трём уровням.
Цветные треугольники (зелёные и красные).
ХОД УРОКА:
Приветствуются учащиеся, гости урока. Сообщается тема урока (Слайд №1).

Учащиеся знакомятся с содержанием эпиграфа и триединых задач урока
(Слайд №2)

Проводится устная работа с учащимися, содержащая два задания: вычислить и охарактеризовать данную функцию по уравнению (Слайд №3).

Перед тем как начать устную работу шести ученикам выдаются карточки, после выполнения первого задания устной работы карточки передаются тем учащимся, которые их будут проверять. По окончании устной работы карточки сдаются учителю.

Проводится фронтальный опрос по теории, соответствующей теме урока
(Слайд №4).

Демонстрируются определения и комментируются ещё раз учителем ответы на вопросы фронтального опроса. (Слайд №5)

Учителем задаётся вопрос учащимся: Кто из вас подобрал высказывания, касающиеся темы сегодняшнего урока и тех вопросов, что были заданы?
Задаётся домашнее задание, содержание которого должно соответствовать уровню знаний каждого ученика. Оформить выполненное домашнее задание необходимо на половинке листа А4 формата (Слайд №6).

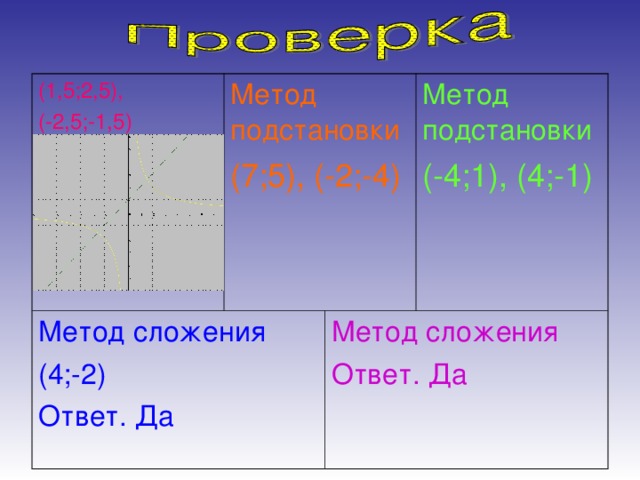
Работа в тетрадях. Учащиеся разбиваются на группы: 1 группа: 1 и 2 стол, 2 группа: 3 и 4 стол, 3 группа: все остальные. Учащимся предлагается решить одну систему уравнений тремя способами. Первой группе – методом подстановки, второй группе – методом сложения, третьей – графическим способом (Слайд № 7).
Каждая группа при этом должна оформить решение системы уравнений на половинке листа ватмана.
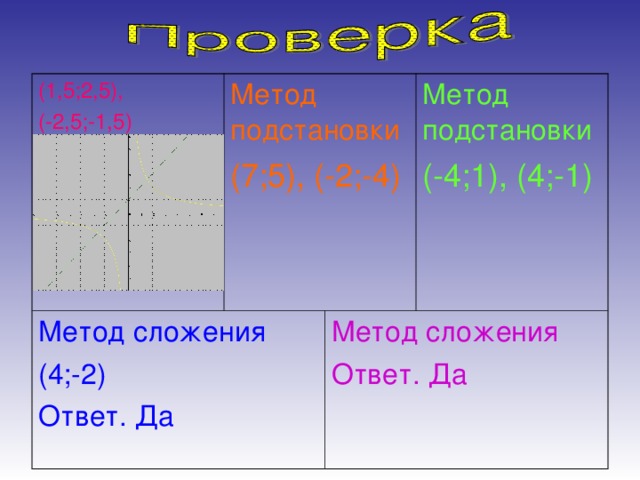
8. Представитель от каждой группы выходит с проектом решения и защищает работу группы. Параллельно на экран выводится решение системы тем или иным методом с выполнением требований к оформлению письменных работ.

Метод сложения (Слайд №8)

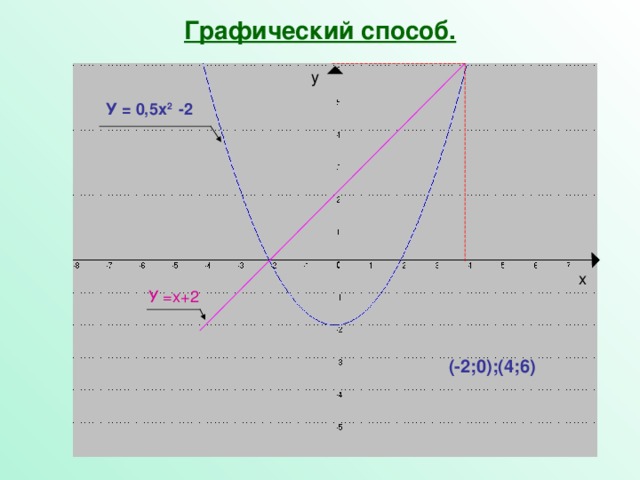
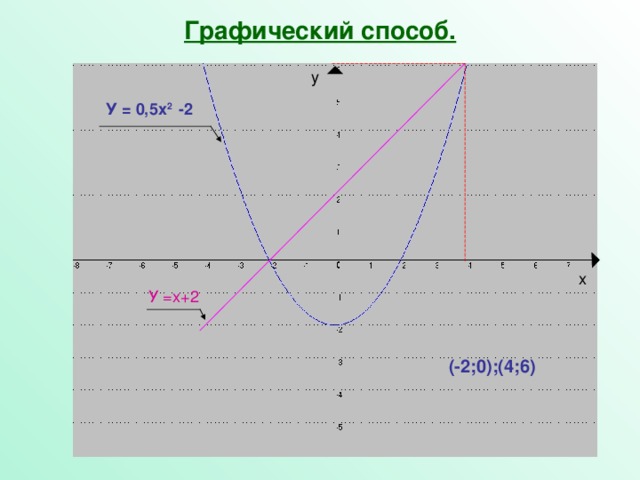
Графический способ (Слайд №9)
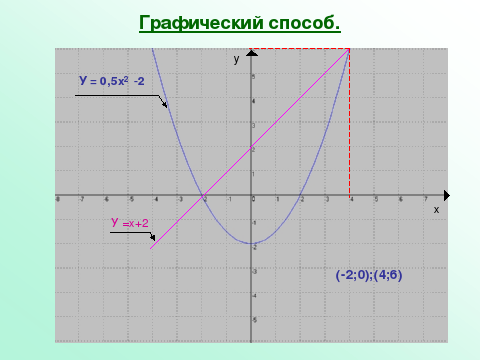
После того как все группы защитили свои проекты решений системы – разминка (Слайд № 10).

Разгадывая ребус, учащиеся должны ответить на вопрос: «Что, по вашему мнению, здесь лишнее и почему?» (Ответ: среди слов кубическая парабола, гипербола, кривая, парабола, прямая лишнее кривая.)
Далее учащиеся продолжают работу в тетрадях. В тетради переписывается условие всех пяти систем уравнений. Вниманию учащихся предлагается решить пять систем уравнений: первому столу – первую, второму столу – вторую, третьему столу – третью, четвёртому столу – четвёртую, а учащимся, сидящим по периметру класса – пятую (Слайд № 11).

По мере выполнения задания учащиеся, сидящие за разными столами (первый – второй, третий – четвёртый, а по периметру друг с другом) обмениваются тетрадями и производят взаимоконтроль, сверяя правильность решения с экраном и выставляя отметки (Слайд № 12).
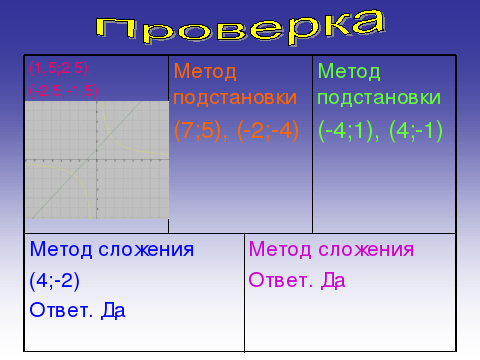
Учащимся, сидящим за компьютером, предлагается на выбор три уровня самостоятельной работы. Тем, кто сидит за рабочими столами без компьютера, на бумажном носителе предлагается самостоятельная работа, соответствующая уровню их знаний. Те из учащихся, кто хочет повысить отметку, выполняет самостоятельную работу сначала на Первый уровень, затем на Второй уровень и Третий – последовательно. На розданных листах ответов каждый ученик заготавливает таблицу: (Слайд № 13)
И по мере выполнения задания самостоятельной работы учащиеся заносят букву правильного ответа в соответствующую графу таблицы. Учащихся, которые раньше всех выполнят самостоятельную работу, возвращаются к выполнению классной работы и подробно прорешивают остальные задания.
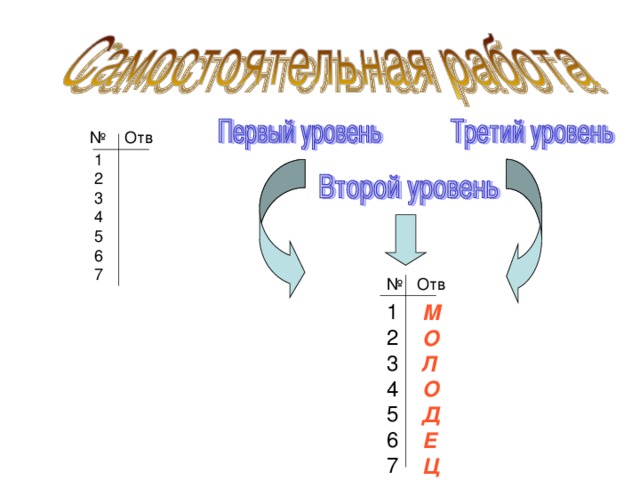
По истечении времени, отведённого на решение самостоятельной работы, показывается экран ответов (Слайд №13)
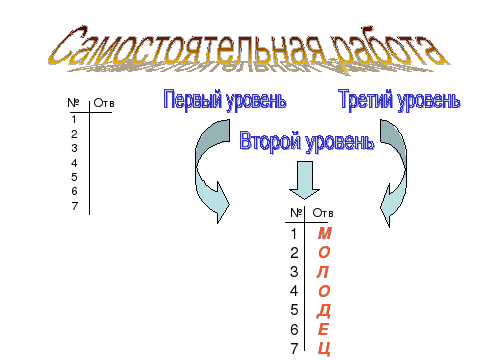
Подводятся итоги урока. Связь с эпиграфом урока. Комментируются отметки. Кто получил в ответах «МОЛОДЕЦ», тот получает отметку 3 – за первый уровень, 4 – за второй уровень, 5 – за третий уровень.
Учитель благодарит всех за участие в уроке и просит выразить поднятием зелёного треугольника – положительное настроение, и красного – отрицательное настроение.
Всего доброго. До новых встреч.
П Р И Л О Ж Е Н И Е.
КАРТОЧКА № 1
Выполнил:___________________________________________
Проверил:____________________________________________
Уравнением какого вида задаётся квадратичная функция?
И) у=х3 У) у=5х+3 М) у=5х2
2. График квадратичной функции называется:
С) квадрат У) гипербола И) парабола
З. Графический способ решения систем уравнений заключается:
М) в построении графиков функций разными цветами;
Н) в построении графиков функций в одной системе координат;
У) в построении графиков функций в разных системах координат.
4. Вершина параболы, заданной уравнением у = (х-3)2+4, находится в точке с координатами:
У) (3;4) С) (-3;4) Н) (-3;-4)
5. Сколько способов решения систем уравнений существует?
И) 2 Н) 1 С) 3.
КАРТОЧКА № 2
Выполнил:___________________________________________
Проверил:____________________________________________
Уравнением какого вида задаётся квадратичная функция?
И) у=х3 У) у=5х+3 М) у=5х2
2. График квадратичной функции называется:
С) квадрат У) гипербола И) парабола
З. Графический способ решения систем уравнений заключается:
М) в построении графиков функций разными цветами;
Н) в построении графиков функций в одной системе координат;
У) в построении графиков функций в разных системах координат.
4. Вершина параболы, заданной уравнением у = (х-3)2+4, находится в точке с координатами:
У) (3;4) С) (-3;4) Н) (-3;-4)
5. Сколько способов решения систем уравнений существует?
И) 2 Н) 1 С) 3.
КАРТОЧКА № 3
Выполнил:___________________________________________
Проверил:____________________________________________
Уравнением какого вида задаётся квадратичная функция?
И) у=х3 У) у=5х+3 М) у=5х2
2. График квадратичной функции называется:
С) квадрат У) гипербола И) парабола
З. Графический способ решения систем уравнений заключается:
М) в построении графиков функций разными цветами;
Н) в построении графиков функций в одной системе координат;
У) в построении графиков функций в разных системах координат.
4. Вершина параболы, заданной уравнением у = (х-3)2+4, находится в точке с координатами:
У) (3;4) С) (-3;4) Н) (-3;-4)
5. Сколько способов решения систем уравнений существует?
И) 2 Н) 1 С) 3.
КАРТОЧКА № 4
Выполнил:___________________________________________
Проверил:____________________________________________
Уравнением какого вида задаётся квадратичная функция?
И) у=х3 У) у=5х+3 М) у=5х2
2. График квадратичной функции называется:
С) квадрат У) гипербола И) парабола
З. Графический способ решения систем уравнений заключается:
М) в построении графиков функций разными цветами;
Н) в построении графиков функций в одной системе координат;
У) в построении графиков функций в разных системах координат.
4. Вершина параболы, заданной уравнением у = (х-3)2+4, находится в точке с координатами:
У) (3;4) С) (-3;4) Н) (-3;-4)
5. Сколько способов решения систем уравнений существует?
И) 2 Н) 1 С) 3.
КАРТОЧКА № 5
Выполнил:___________________________________________
Проверил:____________________________________________
Уравнением какого вида задаётся квадратичная функция?
И) у=х3 У) у=5х+3 М) у=5х2
2. График квадратичной функции называется:
С) квадрат У) гипербола И) парабола
З. Графический способ решения систем уравнений заключается:
М) в построении графиков функций разными цветами;
Н) в построении графиков функций в одной системе координат;
У) в построении графиков функций в разных системах координат.
4. Вершина параболы, заданной уравнением у = (х-3)2+4, находится в точке с координатами:
У) (3;4) С) (-3;4) Н) (-3;-4)
5. Сколько способов решения систем уравнений существует?
И) 2 Н) 1 С) 3.
КАРТОЧКА № 6
Выполнил:___________________________________________
Проверил:____________________________________________
Уравнением какого вида задаётся квадратичная функция?
И) у=х3 У) у=5х+3 М) у=5х2
2. График квадратичной функции называется:
С) квадрат У) гипербола И) парабола
З. Графический способ решения систем уравнений заключается:
М) в построении графиков функций разными цветами;
Н) в построении графиков функций в одной системе координат;
У) в построении графиков функций в разных системах координат.
4. Вершина параболы, заданной уравнением у = (х-3)2+4, находится в точке с координатами:
У) (3;4) С) (-3;4) Н) (-3;-4)
5. Сколько способов решения систем уравнений существует?
И) 2 Н) 1 С) 3.
ПЕРВЫЙ УРОВЕНЬ
К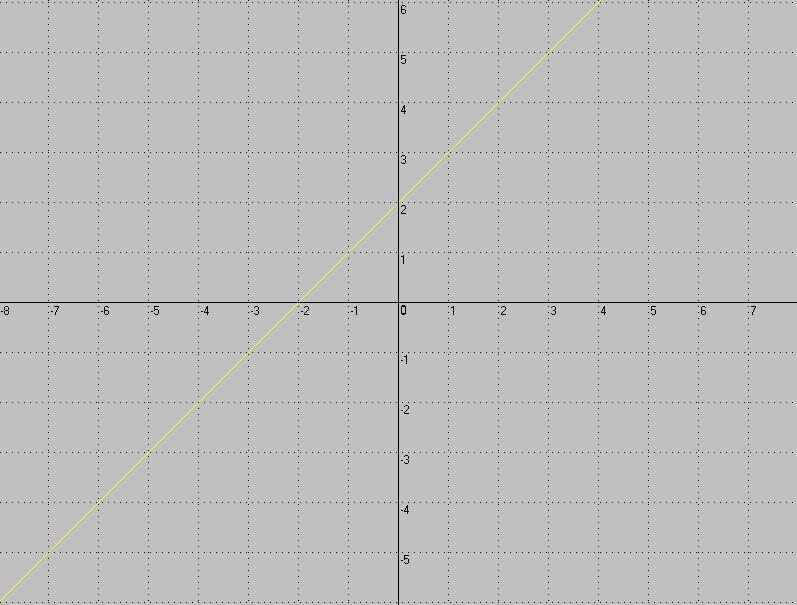 аким уравнением можно задать график, изображённый на рисунке?
аким уравнением можно задать график, изображённый на рисунке?
Л) у = х2 М) у = х+2
Д) у = - х+2 Е) у = - х-2
По графику найти решение системы уравнений
О) (-2,5;-2,5), (2,5;2,5) Д) (3;3), (-3;-3)
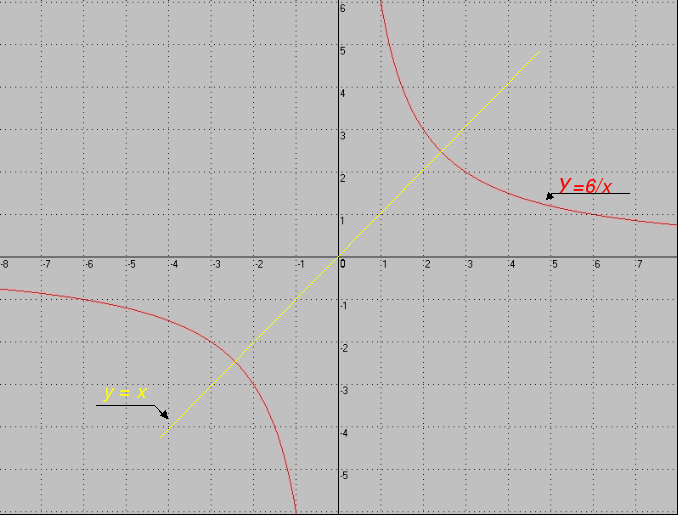 Ц) (3;2,5), (-3;-2,5) М) (-2,5;3), (-2,5;-3)
Ц) (3;2,5), (-3;-2,5) М) (-2,5;3), (-2,5;-3)
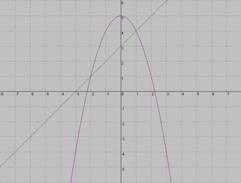
Н а каком рисунке изображено графическое решение системы уравнений?
а каком рисунке изображено графическое решение системы уравнений?
у=х2-5
х2+у2=25
Л) 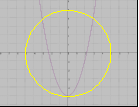 Е)
Е) 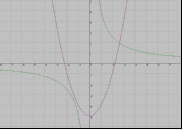
Ж) 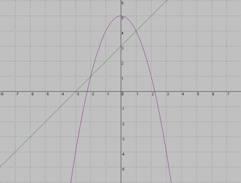 Д)
Д) 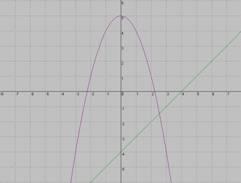
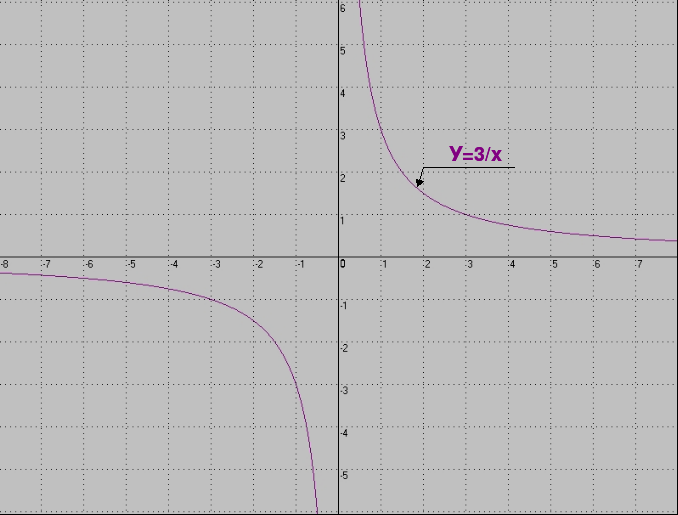
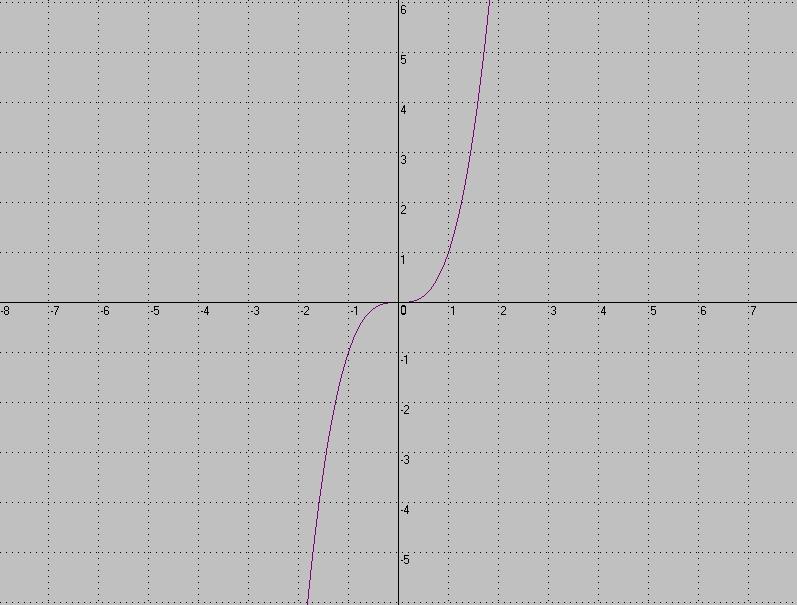
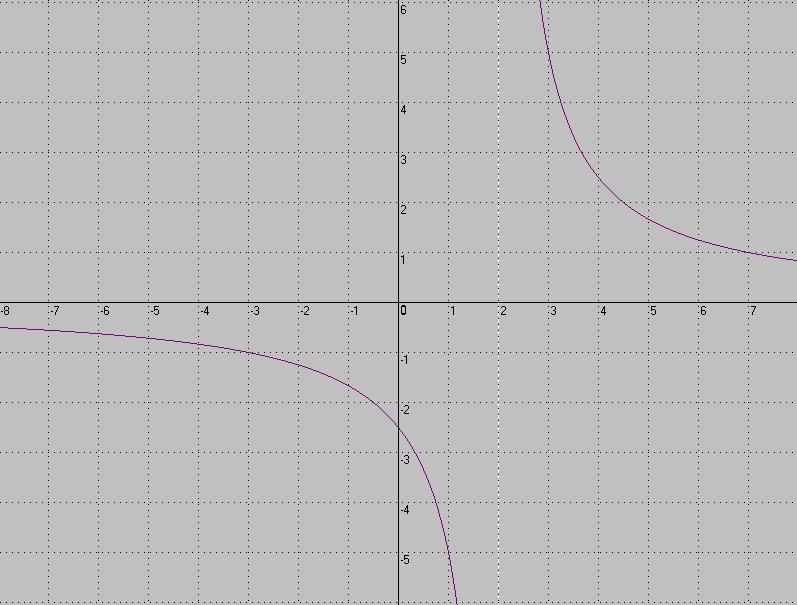
Как называется график функции, изображённый на рисунке?
Е) парабола Д) кубическая парабола
О) гипербола Ц) линейная функция
Какой системе уравнений принадлежит изображённое графическое решение?

А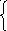
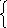
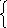
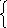 ) у =
) у = Е) у=2х Д) у = - х2+5 Ц) ху=12
Е) у=2х Д) у = - х2+5 Ц) ху=12
у = , у=х2-8, у=х+3, у=х-1
, у=х2-8, у=х+3, у=х-1
Какие пары чисел являются решением системы уравнений?
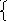
х=7+у
ху=-10
М) (-5;-2); (-2,-5) Е) (2;-5); (5;-2) Ц) (3,4), (-3,-4) Д) (-2;5); (-5;2)
Найдите числа, если сумма двух чисел равна 12, а их произведение равно 32.
Д) (-8;-4), (-8;4) Е) (-8;-4), (8;4) О) (-4;-8), (4;8) Ц) (8;4), (4;8)
 ВТОРОЙ УРОВЕНЬ
ВТОРОЙ УРОВЕНЬ
1.Каким уравнением можно задать график, изображённый на рисунке?
М) у = х2 Л) у = х+2
Д) у = - х+2 Е) у = - х-2
2. По графику найти решение системы уравнений
 О) (-2;1), (1;4) Д) (2;-1), (-1;-4)
О) (-2;1), (1;4) Д) (2;-1), (-1;-4)
Ц) (4;1), (1;-2) М) (-4;1), (-1;-2)
3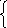 .На каком рисунке изображено графическое решение системы уравнений?
.На каком рисунке изображено графическое решение системы уравнений?
у=х2-5
у =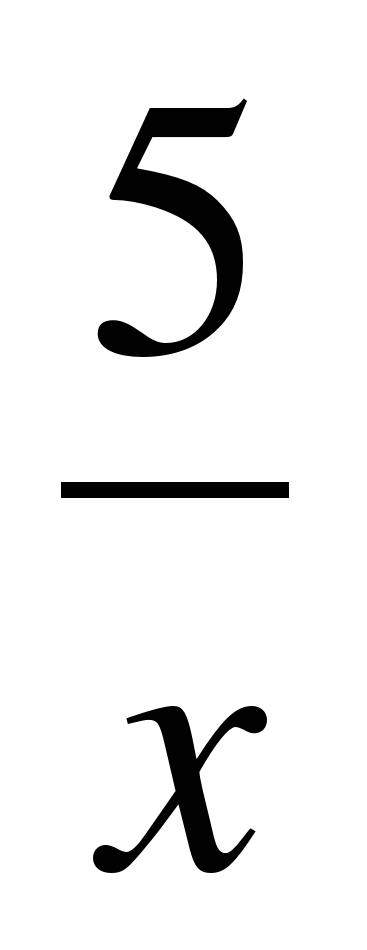
Е)  Л)
Л) 
Ж)  Д)
Д) 
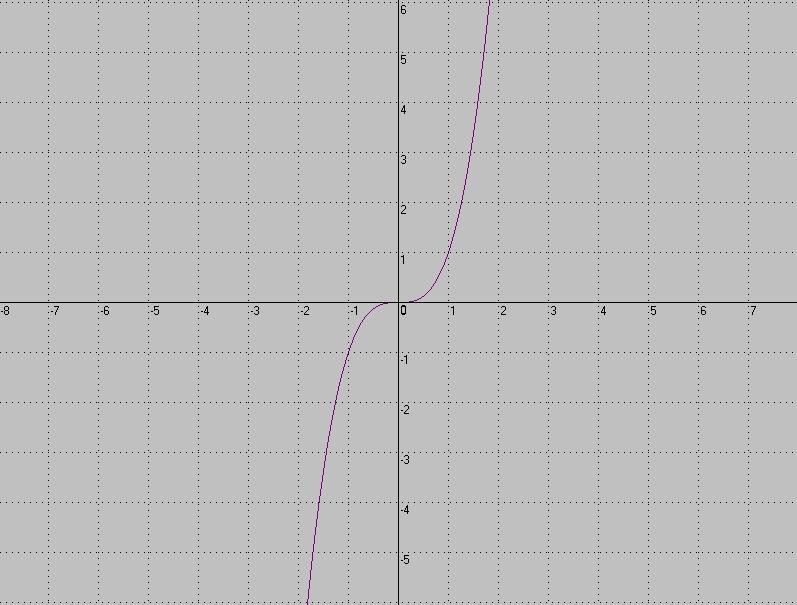
4.Как называется график функции, изображённый на рисунке?
Е) парабола О) кубическая парабола
Д) гипербола Ц) линейная функция
5.Какой системе уравнений принадлежит изображённое графическое решение?

А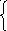
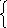
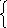
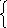 ) у =
) у = Е) у=2х Д) у = х2-5 Ц) ху=12
Е) у=2х Д) у = х2-5 Ц) ху=12
у = , у=х2-8, у2+х2=25, у=х-1
, у=х2-8, у2+х2=25, у=х-1
6.Какая пара чисел является решением системы уравнений?
х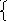 +2у=7
+2у=7
2у2+ху=14
М) (-3;-2); Е) (3;2); Ц) (2,3); Д) (-2;3);
7.Найдите координаты общих точек графиков уравнений х2-9у2=0 и у2+х=10.
Д) (-6;-2), (-15;-5) Е) (2;6), (-5;15) О) (-6;-2), (15;-5) Ц) (6;2), (-15;5)
ТРЕТИЙ УРОВЕНЬ
1.Каким уравнением можно задать график, изображённый на рисунке?
М) у = -х2 +5 Л) у = х+2
Д) у = - х+2 Е) у = - х-2
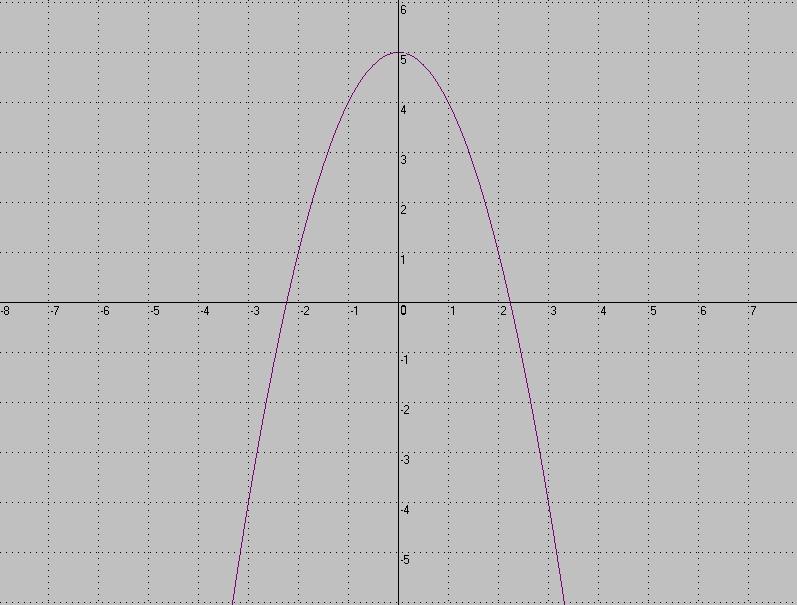
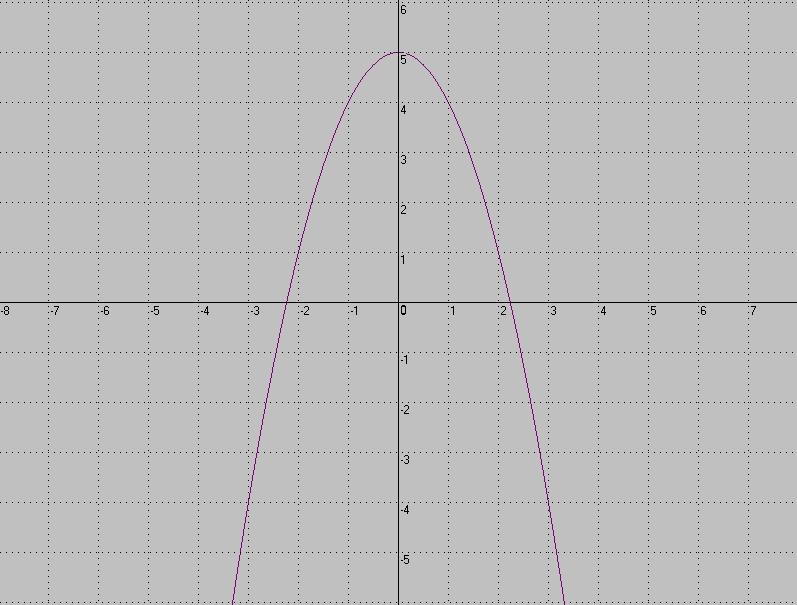
2. По графику найти решение системы уравнений
О) (-3,1;-5), (2,2;0,2) Д) (5;3,1), (0,2;2,2)
Ц) (-5;3,1), (0,2;-2,2) М) (-4;1), (-1;-2)
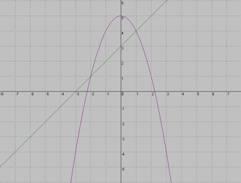
3.На каком рисунке изображено графическое решение системы уравнений?
у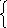 =-х2+5
=-х2+5
у =х-4
Е)  Д)
Д) 
Ж)  Л)
Л) 
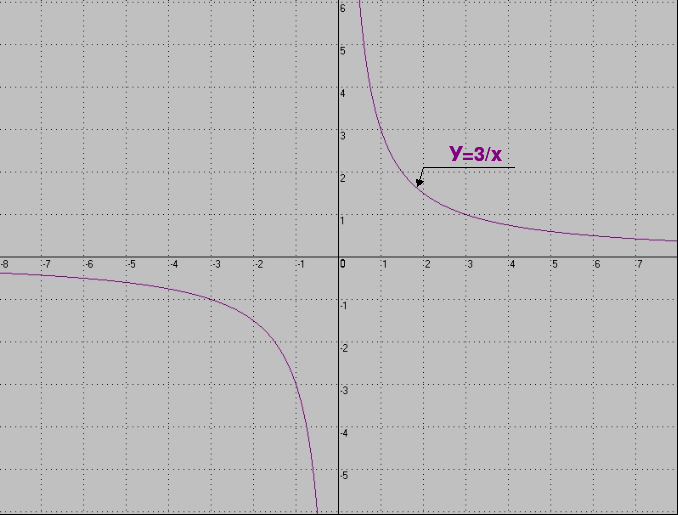
4.Как называется график функции, изображённый на рисунке?
Е) парабола Л) кубическая парабола
О) гипербола Ц) линейная функция
5.Какой системе уравнений принадлежит изображённое графическое решение?
Д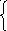
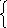
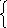
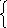 ) у = Е) у=2х А) у = х2-5 Ц) ху=12
) у = Е) у=2х А) у = х2-5 Ц) ху=12
у =, у=х2-8, у2+х2=25, у=х-1
6.Какие пары чисел являются решением системы уравнений?
х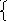 +у=4
+у=4
х2+2ху+2у2=17
М) (-3;-1);(-5;-1) Е) (3;1); (5;-1) Ц) (3,2); (2;3) Д) (1;3);(-1;5)
7.Найдите координаты общих точек графиков уравнений 4х2-у2=0 и х2-у=8.
Д) (-4;-8), (-2;-4) Е) (-4;8), (-2;-4) О) (4;-8), (2;-4) Ц) (4;8), (-2;-4)
 ТРЕТИЙ УРОВЕНЬ
ТРЕТИЙ УРОВЕНЬ О) (-3,1;-5), (2,2;0,2) Д) (5;3,1), (0,2;2,2)
О) (-3,1;-5), (2,2;0,2) Д) (5;3,1), (0,2;2,2)  =-х2+5
=-х2+5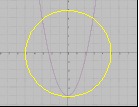 Д)
Д)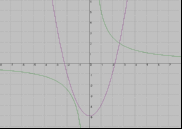
 Л)
Л)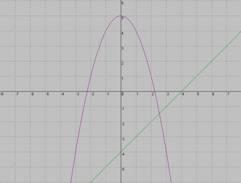
 ак называется график функции, изображённый на рисунке?
ак называется график функции, изображённый на рисунке?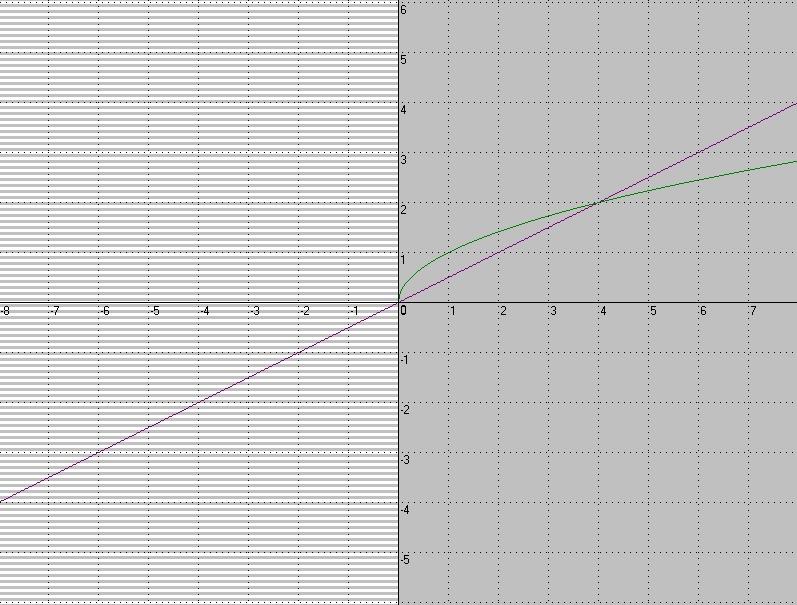
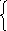
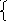 +у=4
+у=4 ВТОРОЙ УРОВЕНЬ
ВТОРОЙ УРОВЕНЬ О) (-2;1), (1;4) Д) (2;-1), (-1;-4)
О) (-2;1), (1;4) Д) (2;-1), (-1;-4) 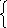 а каком рисунке изображено графическое решение системы уравнений?
а каком рисунке изображено графическое решение системы уравнений?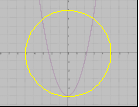 Л)
Л)

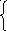
 +2у=7
+2у=7


















 аким уравнением можно задать график, изображённый на рисунке?
аким уравнением можно задать график, изображённый на рисунке? Ц) (3;2,5), (-3;-2,5) М) (-2,5;3), (-2,5;-3)
Ц) (3;2,5), (-3;-2,5) М) (-2,5;3), (-2,5;-3) а каком рисунке изображено графическое решение системы уравнений?
а каком рисунке изображено графическое решение системы уравнений? Е)
Е)
 Д)
Д)

 ВТОРОЙ УРОВЕНЬ
ВТОРОЙ УРОВЕНЬ .На каком рисунке изображено графическое решение системы уравнений?
.На каком рисунке изображено графическое решение системы уравнений?
 аким уравнением можно задать график, изображённый на рисунке?
аким уравнением можно задать график, изображённый на рисунке?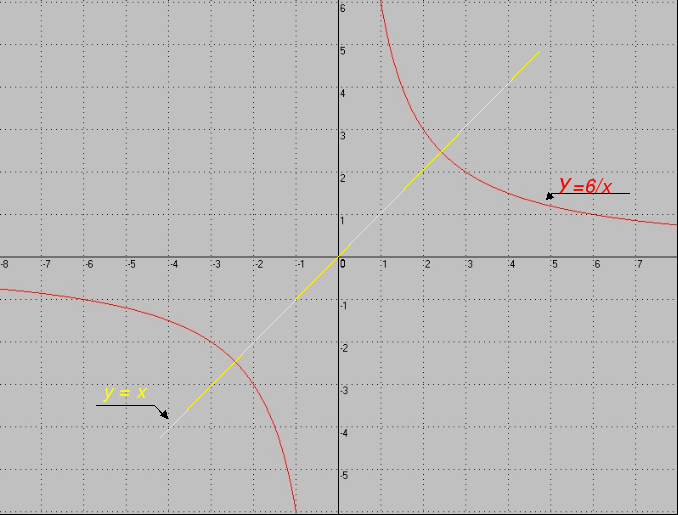 Ц) (3;2,5), (-3;-2,5) М) (-2,5;3), (-2,5;-3)
Ц) (3;2,5), (-3;-2,5) М) (-2,5;3), (-2,5;-3)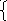 а каком рисунке изображено графическое решение системы уравнений?
а каком рисунке изображено графическое решение системы уравнений? Е)
Е)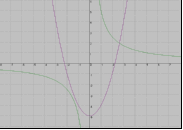
 Д)
Д)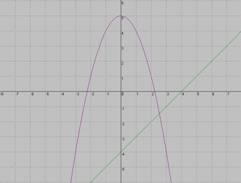
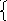
 ТРЕТИЙ УРОВЕНЬ
ТРЕТИЙ УРОВЕНЬ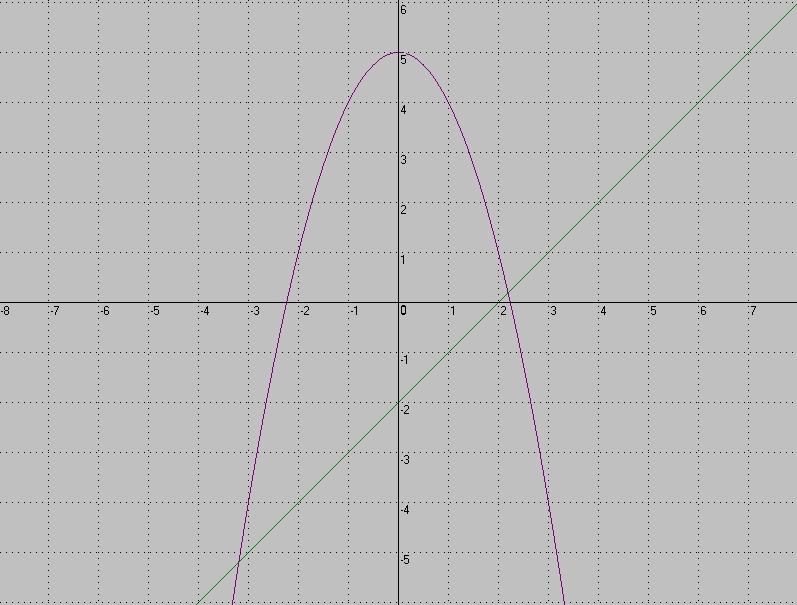 О) (-3,1;-5), (2,2;0,2) Д) (5;3,1), (0,2;2,2)
О) (-3,1;-5), (2,2;0,2) Д) (5;3,1), (0,2;2,2) 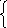 =-х2+5
=-х2+5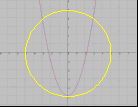 Д)
Д)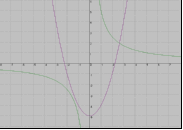
 Л)
Л)
 ак называется график функции, изображённый на рисунке?
ак называется график функции, изображённый на рисунке?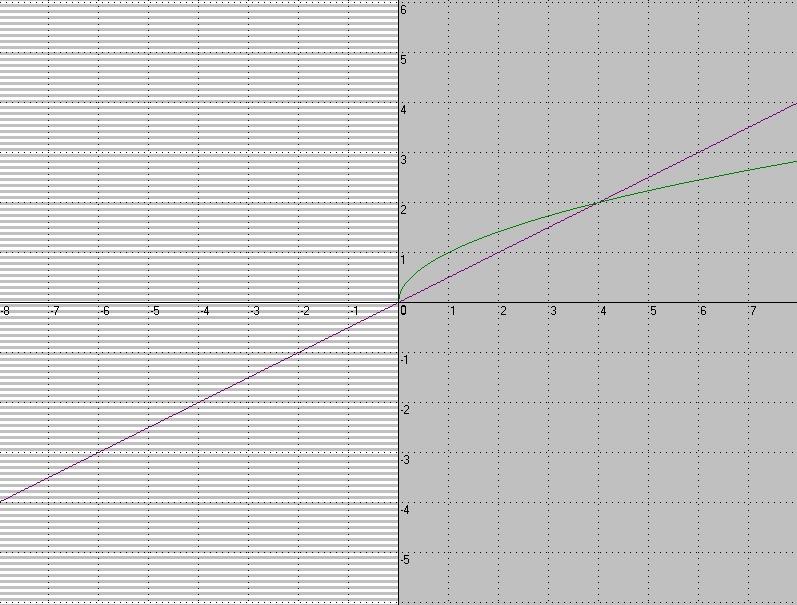

 +у=4
+у=4