Урок-зачет по теме «Четырехугольники»

Геометрия – 8 класс

_{Зачет по теме: « Четырёхугольники»}

Цели урока:

• проверка уровня усвоения теоретических знаний и умения применять их при решении различных задач;

• развитие речи, умения лаконично излагать свои мысли, анализировать и делать выводы;

• воспитание у учащихся интереса к предмету, доброжелательности, умения ра­ботать в коллективе.

Оборудование: кроссворды для каждого ученика; тесты на четыре варианта; мерная веревка и план местности для каждой груп­пы; магнитная доска; изображения Гавсов и банка на магнитах; таблицы построения.

ХОД УРОКА

I.Вводная часть.

Класс разделен на группы по 5-6 человек.

Учитель. Сегодня у нас зачет по теме «Четырехугольники», На уроке вы должны показать свои знания теории по данной теме, т. е. знание определе­ний, свойств и признаков различных четырехуголь­ников, а также умение применять эти знания при решении задач. Зачет пройдет в три этапа:

• решение кроссвордов;

• решение задач;

• тестирование.

Прежде чем приступить к решению кроссвордов, отметьте свое настроение в начале урока в специаль­ных таблицах (поставьте знак «+» в том столбце, где нарисована мордочка, соответствующая вашему на­строению, а с обратной стороны подпишите свою фа­милию). Вторую строчку таблицу вы заполните в кон­це урока (рис. 1).

Начало урока
Конец урока

Рис.1.

II. Решение кроссворда.

Перед вами кроссворд, на решение которого дает­ся __ минут (рис. 2).

1 2 3 4 5 6 7 8 9 10 11

Рис. 2.

По горизонтали:

3. Четырёхугольник, у которого только две противолежащие стороны параллельны.

4. Сумма длин всех сторон четырёхугольника.

6. Ромб, у которого все углы прямые.

7 Отрезок, соединяющий противолежащие вершины четырёхугольника.

8. Параллелограмм, у которого все стороны равны.

10. Параллельные стороны трапеции.

11. Фигура, состоящая из четырёх точек и четырёх последовательно соединяющих их отрезков.

     По вертикали:

1. Параллелограмм, у которого все углы прямые.

2. Отрезок, соединяющий соседние вершины четырёхугольника.

4. Четырёхугольник, у которого противолежащие стороны параллельны.

5. Трапеция, у которой боковые стороны равны.

9. Непараллельные стороны трапеции.

III. Проверка знания теории.

Прежде чем приступить к решению задач, выяс­ним:

• Какая фигура называется четырехугольником?

• Какие вершины четырехугольника называются соседними, какие противолежащими?

• Что такое диагонали четырехугольника?

• Какие стороны четырехугольника называются соседними? Какие стороны называются противолежа­щими?

IV. Решение задач (устно)

• Дайте точное определение параллелограмма и сформулируйте свойства, которыми обладает парал­лелограмм.

Задача 1. Выясните, являются ли фигуры, изоб­раженные на рисунках 3, а—г, параллелограммами.

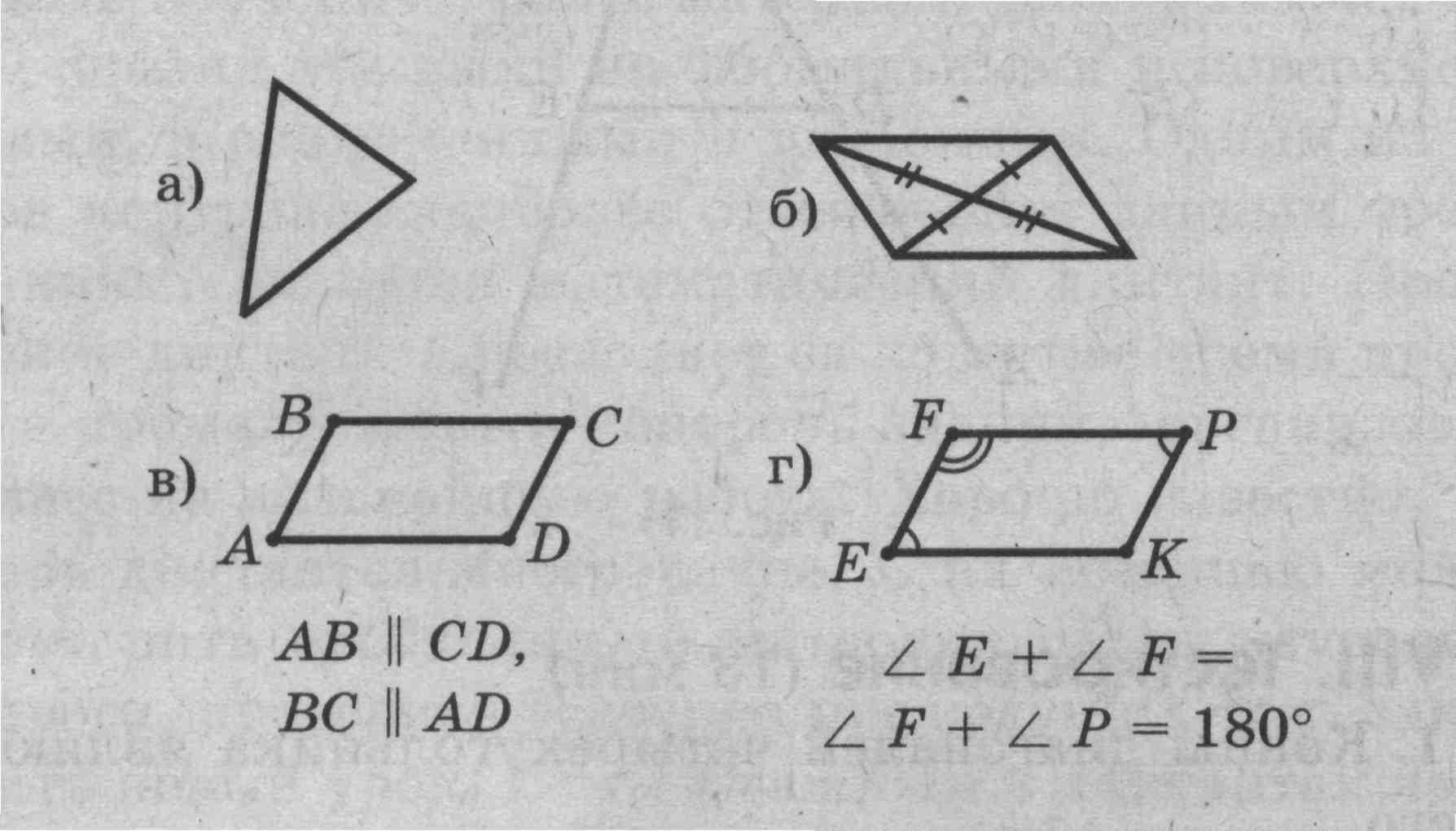Рис. 3

• Дайте определение ромба и сформулируйте свой­ства, которыми обладает ромб.

Задача 2. Выясните, являются ли ромбами изоб­раженные на рисунках 4, а—в четырехугольники.

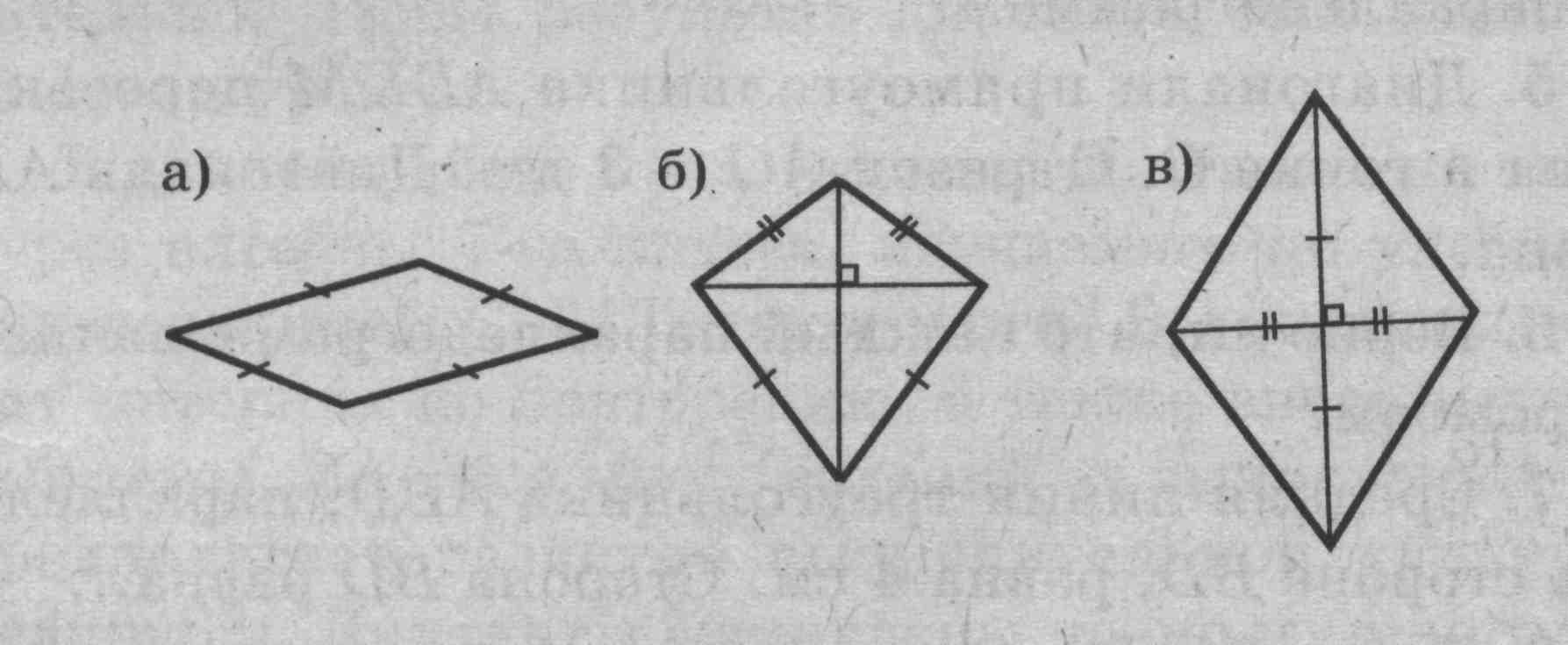Рис. 4

• Дайте определение прямоугольника.

• Каким свойством обладает прямоугольник?

Задача 3. Являются ли прямоугольниками изоб­раженные на рисунках 5, а, б параллелограммы?

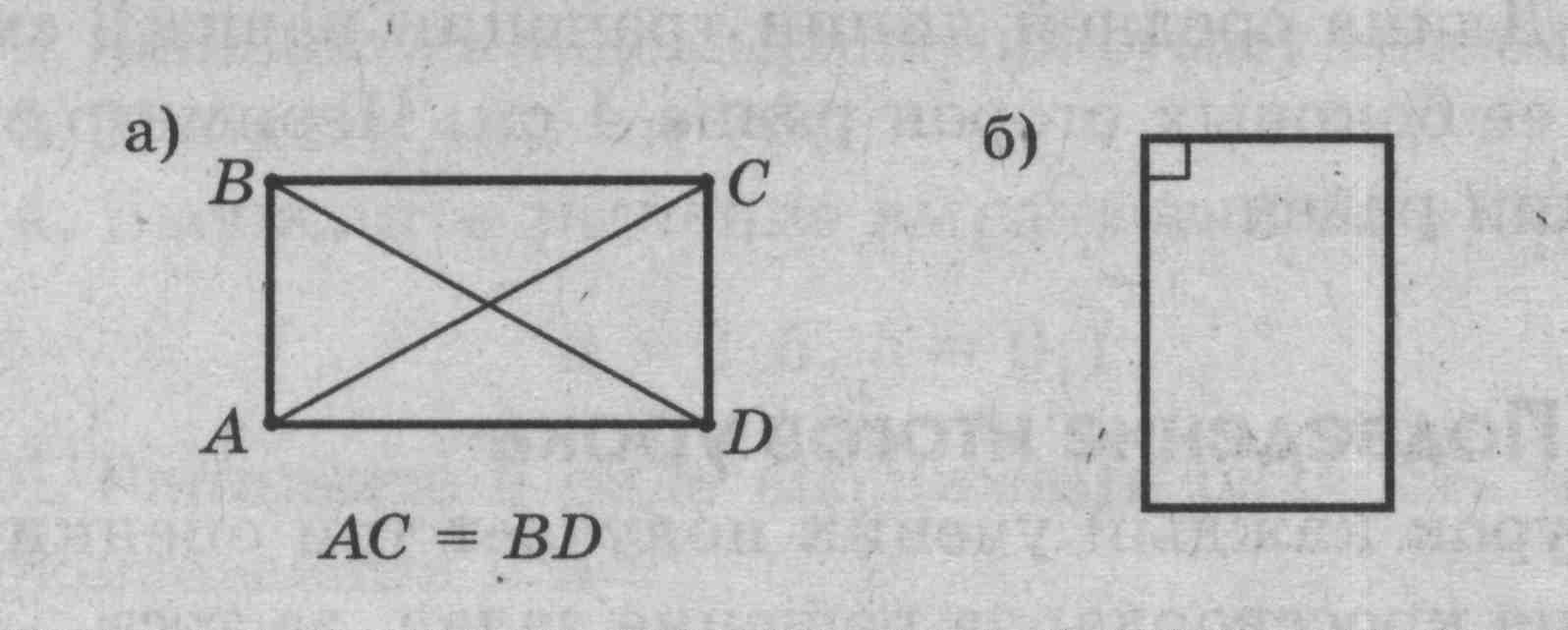Рис. 5

Рассмотрим четырехугольник, который называет­ся трапецией.

• Дайте определение трапеции.

• Как называются параллельные стороны трапе­ции? Непараллельные стороны?

Задача 4. Какие из четырехугольников, приведен­ных на рисунках 6, а-г, являются трапецией? Опре­делите вид.

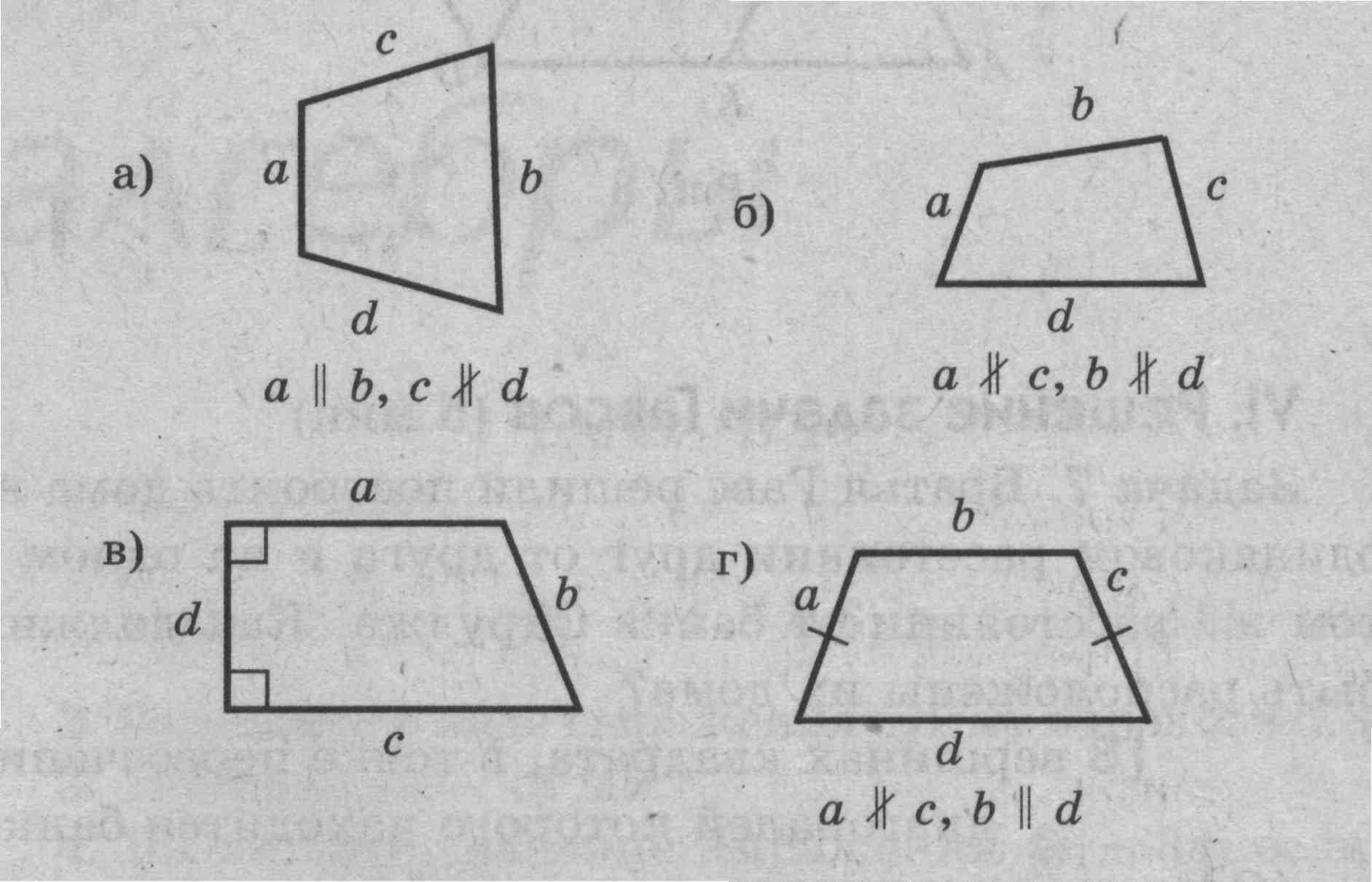Рис. 6

• Какой из известных вам четырехугольников мы еще не рассматривали?

[Квадрат.]

• Что вы можете сказать о квадрате?

V. Решение сложных задач.

Рассмотрим задачи, при решении которых, кроме знаний по теме «Четырехугольники», вам придется вспомнить материал 7-го класса.

Задача 5 (рис. 7).

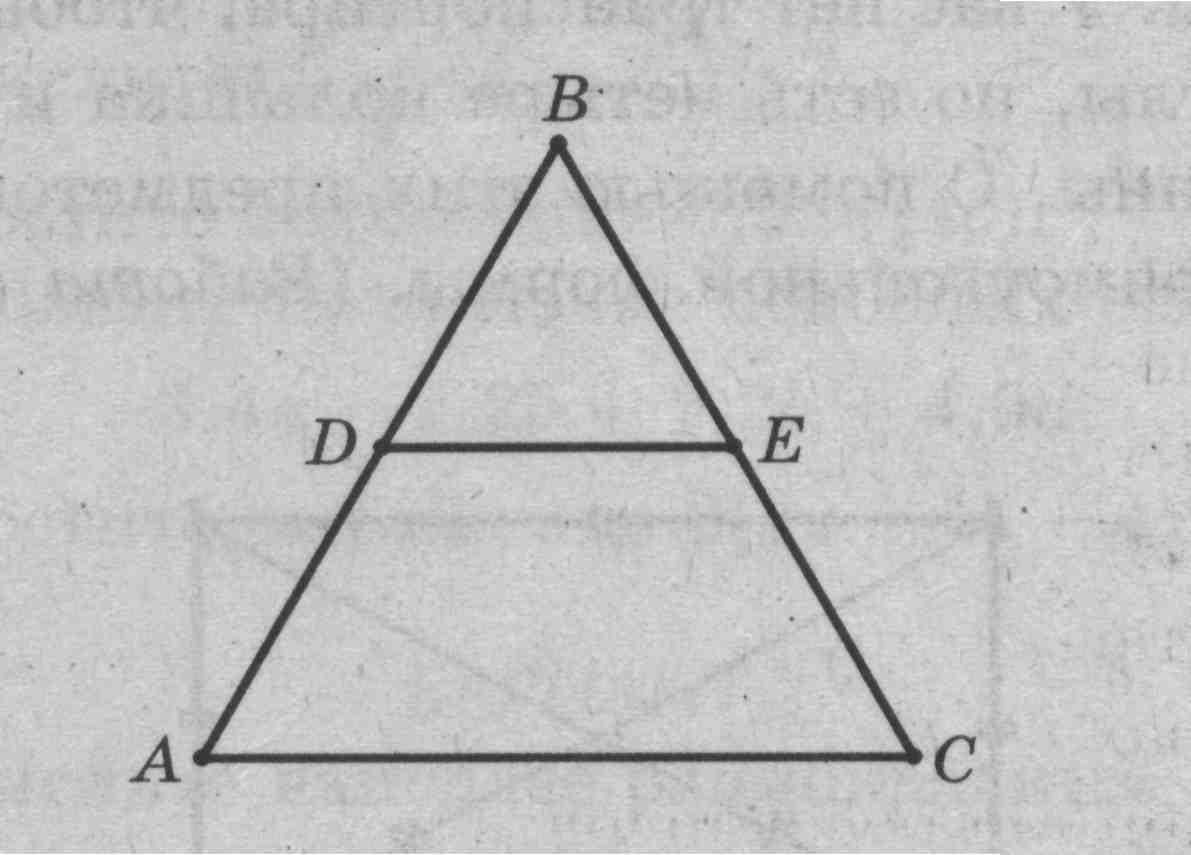
Рис. 7

Дано: 1. ∆ АВС, АВ = ВС. DE - средняя линия. DE = 3 см. РАВС = 16 см. Найти: АВ, ВС, АС.

В этой задаче используется средняя линия тре­угольника.

• Что называется средней линией треугольника?

• Каким свойством обладает средняя линия тре­угольника?

(После обдумывания на местах, один из учени­ков оформляет решение на доске, затем идет обсуж­дение с классом.)

• Какая теорема используется при доказательстве свойства средней линии треугольника? Сформулируй­те ее. (Две формулировки теоремы Фалеса.)

• Какая еще фигура имеет среднюю линию?

• Каким свойством обладает средняя линия тра­пеции?

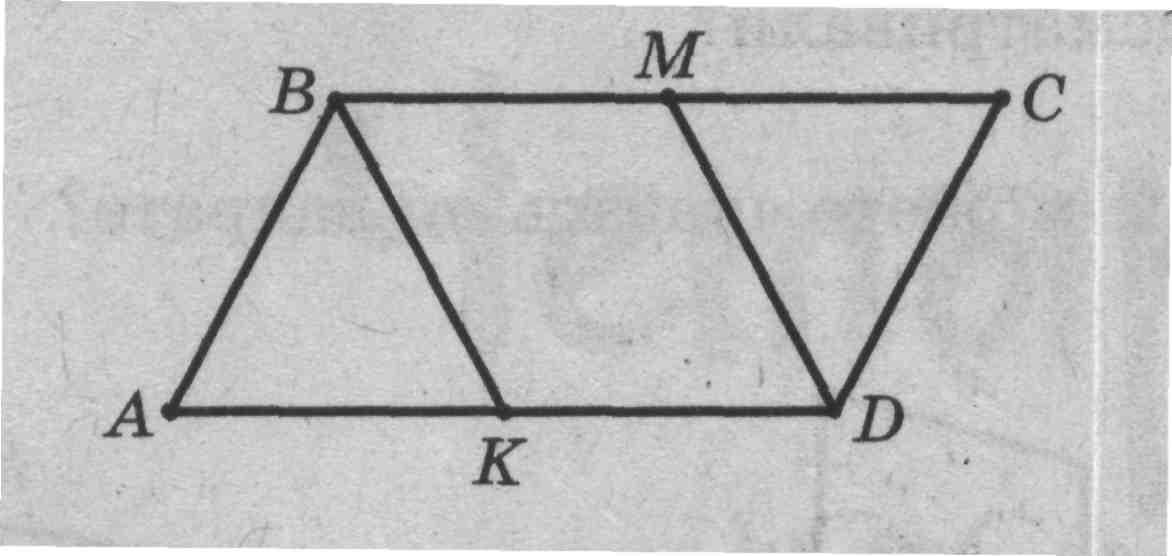Рис. 8

Задача 6 (рис. 8). Дано: 1. ABCD — параллелограмм. 2. ВК, DM - биссектрисы. Определить вид BKDM.

VI. Решение задачи Гавсов.

Задача 7. Братья Гавс решили построить дома на одинаковом расстоянии друг от друга и на одном и том же расстоянии от банка Скруджа. Как должны быть расположены их дома?

[В вершинах квадрата, в точке пересечения диагоналей которого находится банк.] (Один из учеников показывает решение на маг­нитной доске и устно обосновывает его.)

VII. Жизненные ситуации.

Итак, вы владеете определенными теоретически­ми знаниями по теме «Четырехугольники». Посмот­рим, как вы сумеете применить ваши знания при ре­шении жизненных ситуаций.

Задача 8. Представьте, что в результате корабле­крушения вы попали на необитаемый остров. Чтобы где-то жить, нужно построить хижину. Для этого не­обходимо наметить на местности участок прямоуголь­ной формы. У вас нет транспортира, чтобы отметить прямые углы, но есть четыре колышка и 3 веревки разной длины. С помощью этих предметов наметьте участок прямоугольной формы. (Работа в группах; рис. 9.)

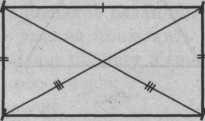
Рис.9

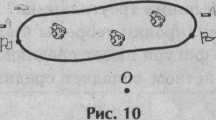
Задача 9. Перенесемся в Америку XVIII в. Вы по­пали в плен к кровожадным охотникам за скальпа­ми - индейцам племени сиу. Вас отпустят только в том случае, если вы измерите расстояние между ла­герем команчей и лагерем семинолов. Лагеря разделяет глубокое озеро, в котором полно аллигаторов, а вы находитесь в точке О. Как можно узнать рассто­яние между лагерями, если в наличии только рулет­ка? (Работа в группах; решение (рис. 10) показыва­ют на плане.)

Задача 10. Для измерения расстояний на местно­сти используют полевой циркуль, состоящий из двух закрепленных в точке В планок и третьей планки DE, скрепляющей середины ножки циркуля. Найдите длину поля, если в нем оказалось сто «шагов» поле­вого циркуля, а планка DE = 1 м (рис. 11).

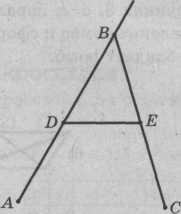
Рис. 11

VIII. Тестирование.

1. Концы диагоналей четырехугольника являются его...

2. Точка М служит серединой отрезков КО и BD. Четырехугольник BKDO называется...

3. Один из углов параллелограмма равен 45°. Осталь­ные его углы равны...

4. Верно ли, что каждый прямоугольник являет­ся параллелограммом?

5. Диагонали прямоугольника АЕКМ пересека­ются в точке О. Отрезок АО = 3 дм. Диагональ AM равна...

6. Верно ли, что каждый параллелограмм являет­ся ромбом?

1. Средняя линия треугольника ABD, параллельная стороне BD, равна 4 см. Сторона BD равна...

2. Точки М, Р и О - середины сторон треугольни­ка ABC. Стороны треугольника МРО равны 3 см, 4 см, 5 см. Периметр треугольника ABC равен...

3. Две параллельные прямые пересечены двумя непараллельными прямыми. Получившийся при этом четырехугольник называется...

4. Точки А и В лежат на боковых сторонах трапеции. Отрезок АВ параллелен основаниям трапеции. Обязательно ли АВ - средняя линия трапеции?

5. Длина средней линии трапеции равна 3 см, а сумма ее боковых сторон равна 4 см. Периметр этой трапеции равен...

IX. Подведение итогов урока

За урок каждый ученик получает три оценки: за решение кроссворда, за решение задач, за тест.

1 2 3 4 5 6 7 8 9 10 11 По горизонтали: 3. Четырёхугольник, у которого только две противолежащие стороны параллельны. 4. Сумма длин всех сторон четырёхугольника. 6. Ромб, у которого все углы прямые. 7 Отрезок, соединяющий противолежащие вершины четырёхугольника. 8. Параллелограмм, у которого все стороны равны. 10. Параллельные стороны трапеции. 11. Фигура, состоящая из четырёх точек и четырёх последовательно соединяющих их отрезков.      По вертикали: Параллелограмм, у которого все углы прямые. 2. Отрезок, соединяющий соседние вершины четырёхугольника. 4. Четырёхугольник, у которого противолежащие стороны параллельны. 5. Трапеция, у которой боковые стороны равны. 9. Непараллельные стороны трапеции.

1 2 3 4 5 6 7 8 9 10 11 По горизонтали: 3. Четырёхугольник, у которого только две противолежащие стороны параллельны. 4. Сумма длин всех сторон четырёхугольника. 6. Ромб, у которого все углы прямые. 7 Отрезок, соединяющий противолежащие вершины четырёхугольника. 8. Параллелограмм, у которого все стороны равны. 10. Параллельные стороны трапеции. 11. Фигура, состоящая из четырёх точек и четырёх последовательно соединяющих их отрезков.      По вертикали: Параллелограмм, у которого все углы прямые. 2. Отрезок, соединяющий соседние вершины четырёхугольника. 4. Четырёхугольник, у которого противолежащие стороны параллельны. 5. Трапеция, у которой боковые стороны равны. 9. Непараллельные стороны трапеции.

1 2 3 4 5 6 7 8 9 10 11	1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11	1 2 3 4 5 6 7 8 9 10 11

Начало урока Конец урока 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.	Начало урока Конец урока 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
Начало урока Конец урока 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.	Начало урока Конец урока 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.

Начало урока Конец урока

Начало урока Конец урока