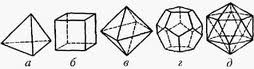
Тема урока: Правильные многогранники.
Цели:
Обучающая:
Систематизировать знания студентов о правильных многогранниках.
Развивающая:
Способствовать развитию пространственного воображения.
Способствовать расширению кругозора.
Воспитывающая:
Формирование интереса к предмету.
Воспитывать активность, творчество, самостоятельность.
Повышение общекультурного уровня студентов.
Тип: Комбинированный урок.
Вид: Урок – ролевая игра
Методы: репродуктивный, информационный, проблемно-эвристический.
Материально-техническое оснащение:
Модели, слайды, отдельные страницы рабочей тетради.
Урок проходит в компьютерном классе.
Ход урока:
Организационный момент. Постановка цели урока. Мотивация.
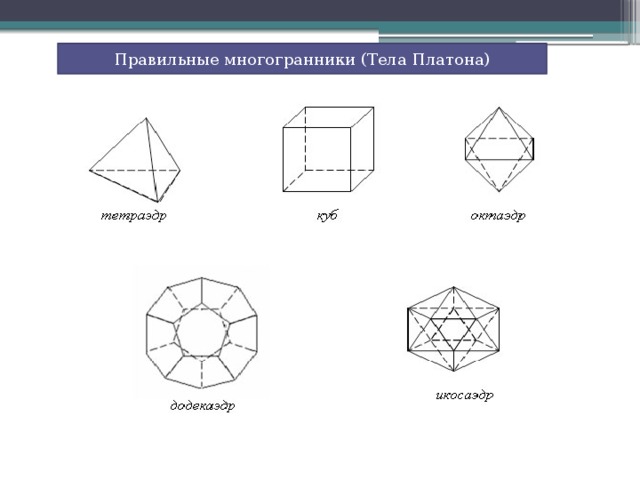
Мы с вами завершаем тему «Многогранники» и тема сегодняшнего урока: «Правильные многогранники».
Наша цель: систематизировать знания о правильных многогранниках. (слайд)
Но урок мы проведем не совсем обычно. Во первых, это будет урок – ролевая игра.
А во- вторых, несколько лет я разрабатываю рабочую тетрадь по математике, и сегодня мы будем пользоваться одной из страниц этой тетради. Возможно, вы оцените ее преимущества перед обычными тетрадями.
Но сначала, давайте вспомним, что мы изучали на предыдущих уроках.
Актуализация опорных знаний.
Пользуясь моментом, хочу продемонстрировать изготовленные модели – внеаудиторную работу ваших товарищей. Работа с моделями:
Все ли представленные модели являются многогранниками?
Что такое многогранник? Дайте определение.
Какие виды многогранников мы изучили?
Из каких элементов состоит каждый из многогранников? Ребра, вершины, грани.
Как вы думаете, а чем правильный многогранник отличается от просто многогранника?
Посмотрите на экран:
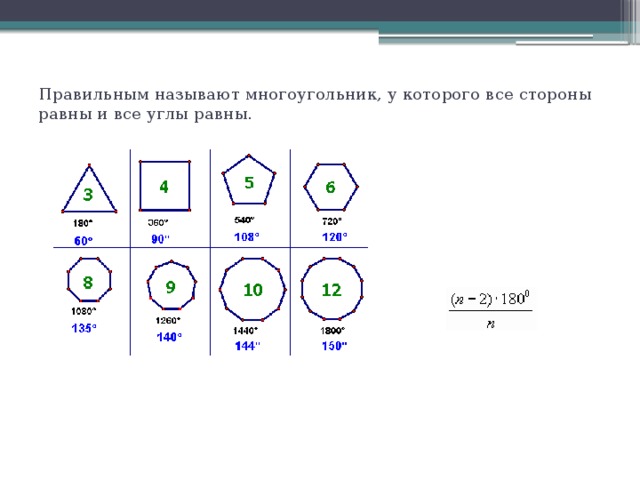
Какой из многоугольников, представленных на слайде, является правильным? Почему? (слайд)
Выберите правильный треугольник. Что вы можете про него рассказать.
Как называется правильный четырехугольник? Охарактеризуйте его свойства.
Какие виды правильных многоугольников вы еще знаете? (слайд)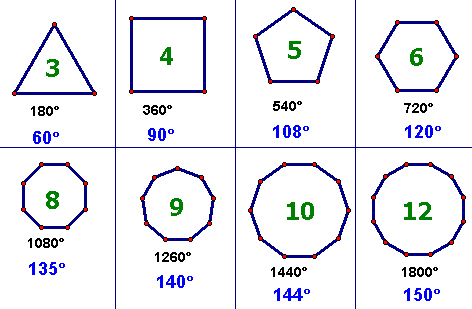
Правильным называют многоугольник, у которого все стороны равны и все углы равны.
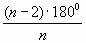
 =
=
Формирование новых понятий и способов действий.
Изучение нового материала Мне хотелось бы начать со слов Бертрана Рассела, которые являются эпиграфом к нашей теме: "Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства”.(слайд)
Название "правильные” идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке.
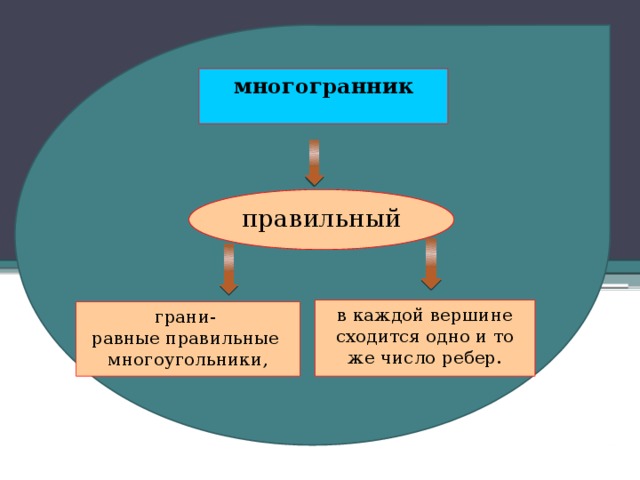
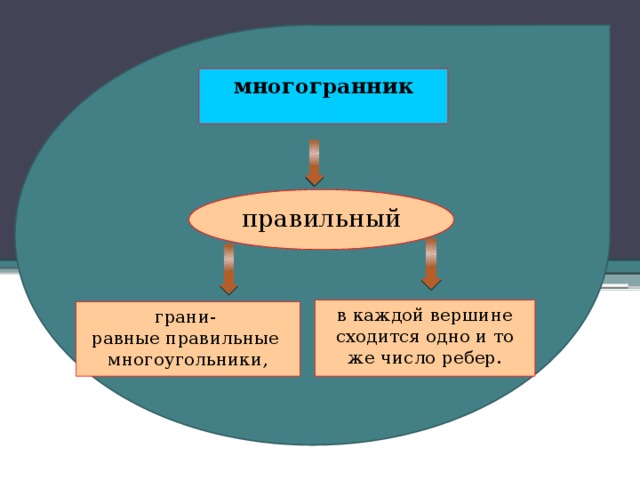
Правильные многоугольники – это многоугольники, у которых все стороны и все углы равны, правильные многогранники – это многогранники, ограниченные правильными и одинаковыми многоугольниками.
Выпуклый многогранник называется правильным, если все его грани – правильные многоугольники и в каждой его вершине сходится одно и то же число ребер. (слайд)
Давайте запишем это определение.
Дальше урок мы проведем в виде игры, которую назовем так:
«ВЫБОРЫ ПРЕЗИДЕНТА МНОГОГРАННИКОВ». (слайд)
Распределим роли:
Избирательная комиссия:
Председатель центральной избирательной комиссии.
Секретарь избирательной комиссии.
Члены комиссии.
Кандидаты в лидеры.
Электорат: слушает, выбирает, голосует.
Небольшое отступление: Кто такой президент? Высшее должностное лицо.
Кто может им стать?...
Говоря математическим языком, он со всех сторон должен быть правильным.
Игра включает в себя следующие этапы:
1. выдвижение кандидатов в президенты;
2. представление кандидатов;
3. проведение выборов.
Итак, слово предоставляю председателю избирательной комиссии:
Ролевая игра: «ВЫБОРЫ ПРЕЗИДЕНТА МНОГОГРАННИКОВ».
ПРЕДСЕДАТЕЛЬ. Понятие многогранника является одним из центральных в курсе геометрии. Теория многогранников имеет богатую и древнюю историю, связанную с именами Пифагора, Евклида, Архимеда, Аполлония. (слайд) Многогранники выделяются своими интересными свойствами и красивыми формами. Но ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. И сегодня нам предстоит выбрать президента многогранников. Естественно, им должен быть один из правильных многогранников. Поэтому напомню определение правильных многогранников.
Выпуклый многогранник называется правильным, если все его грани – правильные многоугольники и в каждой его вершине сходится одно и то же число ребер. (слайд)
Ну, а теперь начнем предвыборную кампанию. Необходимо выбрать кандидатов. (слайд)
СЕКРЕТАРЬ.
Сначала рассмотрим случаи, когда грани многогранника - равносторонние треугольники.
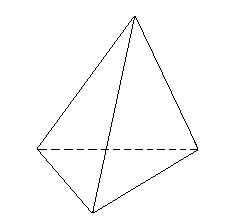
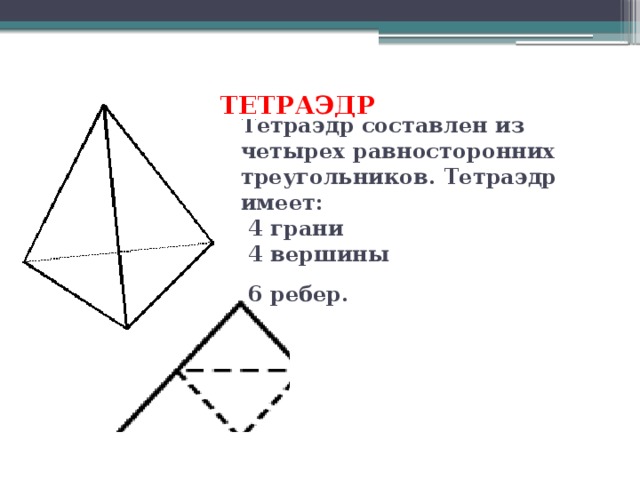
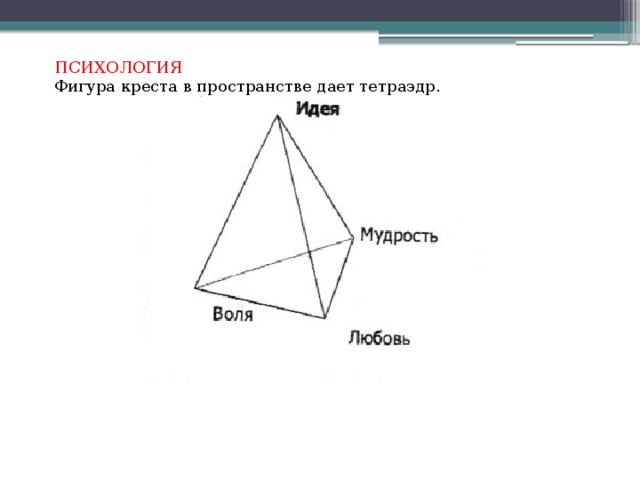
ТЕТРАЭДР. В качестве кандидата, предлагаю тетраэдр. У него все грани равносторонние треугольники и к каждой вершине сходится 3 ребра. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°.
СЕКРЕТАРЬ. Нарушений нет? Зарегистрируем его. (слайд)
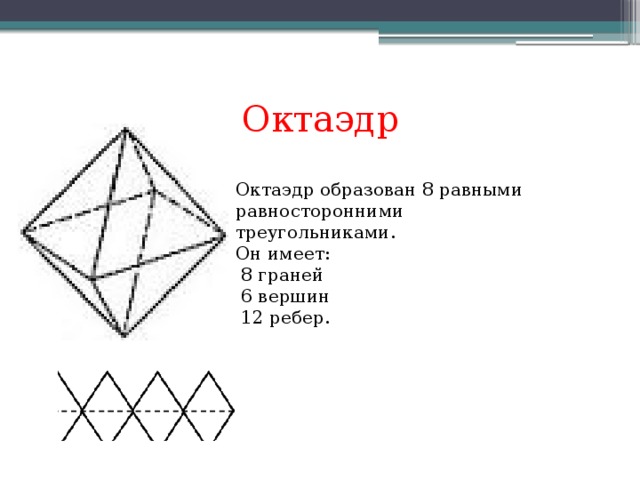
ОКТАЭДР. Если к предыдущей развертке вершины добавить еще один треугольник, то в сумме получится 240°. Это развертка вершины октаэдра.
Поэтому предлагаю в качестве кандидата октаэдр. Он состоит из 8 граней – равных равносторонних треугольников и к каждой его вершине сходится одно и то же число ребер (4)
СЕКРЕТАРЬ. Нарушений нет? Зарегистрируем его. (слайд)
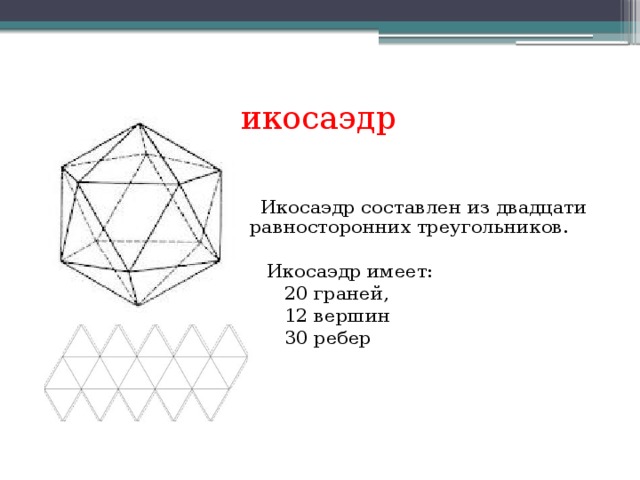
ИКОСАЭДР. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Поэтому предлагаю своего кандидата. Икосаэдр состоит из 20 равных равносторонних треугольников и к каждой его вершине сходится одно и то же число ребер.
СЕКРЕТАРЬ. Нарушений нет? Зарегистрируем его. (слайд)
Еще предложения по выдвижению кандидатов из равносторонних треугольников? Предложений больше нет.
Теперь перейдем к квадратным граням.
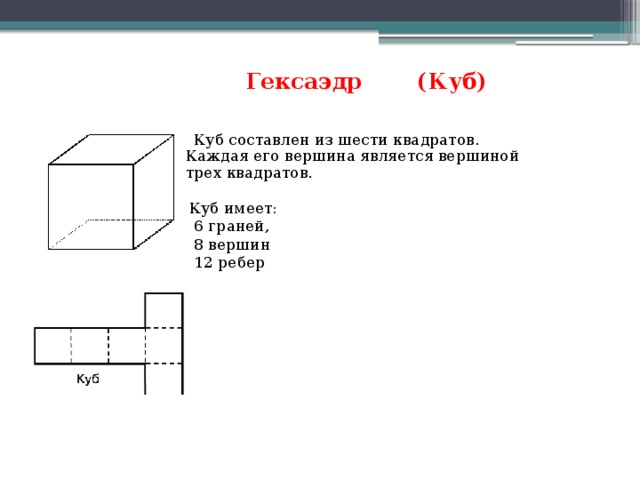
КУБ. Предлагаю в качестве кандидата куб. Развертка из трех квадратных граней имеет угол 3*90°=270° - получается вершина куба, который также называют гексаэдром.
СЕКРЕТАРЬ. Нарушений нет? Зарегистрируем его. (слайд)
Есть еще предложения от правильных многогранников, грани которых имеют форму квадрата?
Предложений больше нет.
Переходим к пятиугольникам.
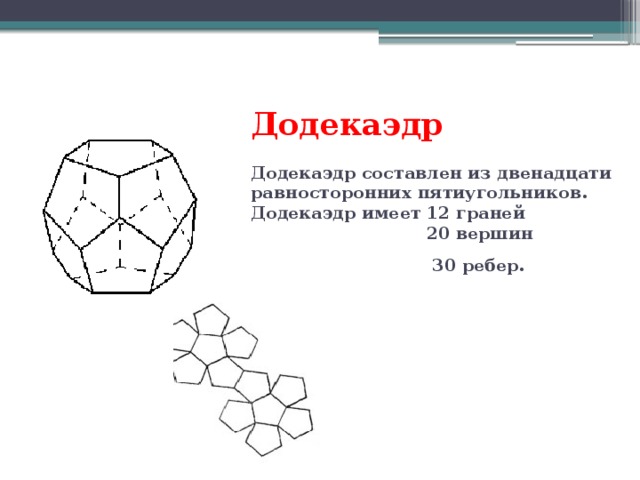
ДОДЕКАЭДР. Среди наших представителей, я один. Три пятиугольные грани дают угол развертки 3*108°=324° - вершина додекаэдра. К каждой вершине сходится 3 ребра.
СЕКРЕТАРЬ. Нарушений нет? Зарегистрируем его. (слайд)
ШЕСТИУГОЛЬНИК. Я достаточно красив и также претендую на место среди правильных многогранников. А название многогранника, который мы можем из меня получить, придумаем сами.
СЕКРЕТАРЬ. Возражение. Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.
ПРЕДСЕДАТЕЛЬ. Итак, регистрация закончена, мы выяснили, что правильных многогранников, а значит и кандидатов на пост президента только 5. (слайд)
Подтверждая это, хочу обобщить вышесказанное:
В самом деле, для того, чтобы получить правильный многогранник, согласно его определению, в каждой вершине должно сходиться одинаковое число граней, каждая из которых является правильным многоугольником.
Сумма плоских углов многогранного угла должна быть меньше 3600, иначе никакой многогранной развертки не получиться.
60 к
к
но к 2, значит,
к=3,4,5 к=3 к=3
Т.о. правильных многогранников всего 5. Их еще называют телами Платона.
Преподаватель: У вас в тетради уже сделаны чертежи представленных многогранников. Давайте подпишем каждый из них, чтобы было в дальнейшем легче ориентироваться. Таким образом создадим портрет каждого из представленных многогранников.
Формирование навыков умственного труда.
ПРЕДСЕДАТЕЛЬ. Следующий этап – это представление кандидатов. (слайд)
Электорату в процессе представления кандидата рекомендуется фиксировать достижения, чтобы выбор будущего президента был объективным.
Преподаватель : Отмечайте в соответствующей клетке знаком «+» или «-». Например, история+
Возможно, в процессе работы у вас будут дополнения. Для этого оставлены соответствующие клетки.
СЕКРЕТАРЬ. Слово представителю тетраэдра. (слайд)
ТЕТРАЭДР. Название тетраэдр в переводе с греческого означает «четырехгранник». «Тетра»- 4, «эдр» -грань. Он составлен из четырех равносторонних треугольников. Имеет 4 вершины и 6 ребер. Тетраэдр был известен с глубокой древности. В философской концепции Платона об устройстве мироздания он символизировал огонь. (слайд)
Пифагор и его ученики также считали, что огонь состоит из мельчайших (а потому невидимых) частиц, имеющих форму тетраэдра. Они обосновывали это тем, что среди выпуклых тел, тетраэдр обладает наименьшим числом граней и наиболее острыми многогранными углами при вершинах, то он обладает наибольшей проникающей способностью (как огонь).
Тетраэдр является простейшим из пяти Платоновых тел, однако, несмотря на это он очень значим, его можно увидеть в различных областях наук, да и просто в жизни.
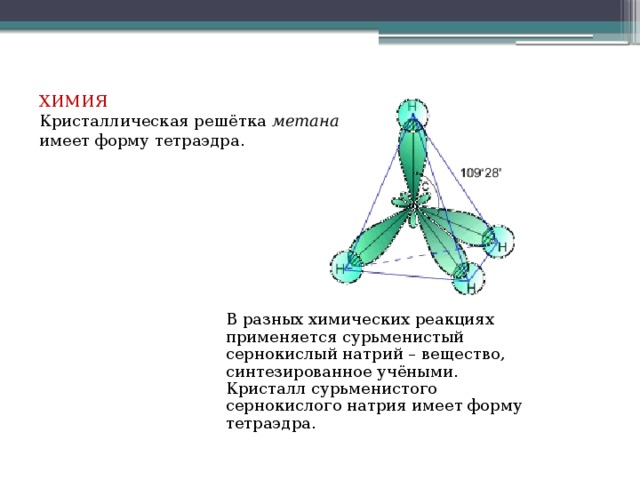
Например, в природе многие кристаллы имеют форму тетраэдра. (слайд)
Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролѐтов зданий, перекрытий, балок, и т.д. например, здание будущего (слайд)
Тетраэдр обладает высокой прочностью при малом весе.
Некоторые парапсихологи отождествляют тетраэдр с крестом. (слайд)
СЧИТАЮ, что этот кандидат достоин быть президентом многогранников.
СЕКРЕТАРЬ. Спасибо. Слово представителю куба.
КУБ. Куб не менее знаменит, чем тетраэдр и также относится к телам Платона. (слайд)
Куб состоит из 6 квадратов, а шестигранник в переводе с греческого - «ГЕКСАЭДР»
Таким образом, он имеет 6 граней, 8 вершин и 12 ребер.
Куб является самым устойчивым многогранником, поэтому в концепции Платона, он символизировал землю и его отождествляли с твердым состоянием. (слайд)
Возможно, что в своей простоте куб не самый привлекательный многогранник. Но он обладает несколькими удивительными свойствами в отношении других Платоновых тел.
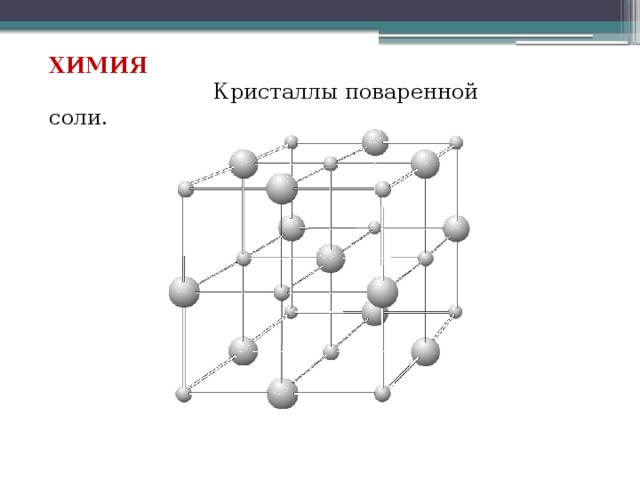
Природа реализовала куб в виде кристалла соли. (слайд)
Кубами можно заполнить все пространство. (слайд)
Современная архитектура также использует кубические конструкции(слайд)
В многочисленных легендах и сказках кубики играют роль решающего судьбу инструмента, выносящего решение. И даже модельеры используют куб в своих нарядах. (слайд)
СЧИТАЮ, что этот кандидат достоин быть президентом многогранников.
СЕКРЕТАРЬ. Спасибо. Слово представителю октаэдра.
ОКТАЭДР. Название «Октаэдр» также греческого происхождения и означает «восьмигранник», так как он образован 8 равным равносторонними треугольниками. (слайд)
Он имеет 6 вершин и 12 ребер. Считается, что октаэдр самый воздушный и в философской концепции Платона он символизировал воздух. (слайд)
При производстве алюминия пользуются алюминиево-калиевыми кварцами, монокристалл которых имеет форму октаэдра. (слайд)
Правильная форма алмаза имеет форму октаэдра. (слайд)
СЧИТАЮ, что этот кандидат достоин быть президентом многогранников.
СЕКРЕТАРЬ. Спасибо. Слово представителю икосаэдра.
ИКОСАЭДР. В переводе с греческого икосаэдр означает двадцатигранник. (слайд)
Он составлен из двадцати равносторонних треугольников. Таким образом, он имеет 20 граней, 12 вершин и 30 ребер. В философии Платона икосаэдр символизировал воду, как самый обтекаемый. (слайд)
Икосаэдр часто встречается в живой природе. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр (слайд) Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление толщи воды.
Икосаэдр передает форму кристаллов бора. (слайд)
В свое время бор использовался для создания полупроводников первого поколения. (слайд)
Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр. (слайд)
По данным некоторых ученых икосаэдр обладает свойствами гармонизации человека и пространства:
икосаэдр со стороной 5 см устраняет психологические зависимости, восстанавливает биоструктуру, гармонизирует личность, очищает структуру места в радиусе 100 м;
икосаэдр со стороной 3 см улучшает связь с подсознанием, гармонизирует взаимоотношения с другими людьми, повышает энергетический уровень в радиусе 200 м, восстанавливает связь человека с землей и космосом, восстанавливает щитовидную железу; способствует реализации собственной миссии в соответствии с программой воплощения;
икосаэдр со стороной 1 см усиливает энергетическую мощность и интеллект человека, улучшает судьбу, восстанавливает энергетику места, выравнивает психику; (слайд)
СЧИТАЮ, что этот кандидат достоин быть президентом многогранников.
СЕКРЕТАРЬ. Спасибо. Слово представителю додекаэдра.
ДОДЕКАЭДР.
Название «додекаэдр» означает 12гранник. (слайд) Додекаэдр составлен из двенадцати равносторонних пятиугольников. Таким образом, додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Вы можете заметить, что мои конкуренты олицетворяли четыре стихии: тетраэдр-огонь, куб-землю, икосаэдр-воду и октаэдр-воздух, а что же мне? (слайд)
По мнению Платона, додекаэдр символизировал весь мир и почитался главнейшим.
Существует предположение, что форму додекаэдра древние греки получили, рассматривая кристаллы пирита (сернистого колчедана FeS). (слайд)
Вирус полиомиелита имеет форму додекаэдра. (слайд)
На картине Сальвадора Дали «Тайная вечеря», Христос и его ученики изображены сидящими внутри огромного прозрачного додекаэдра. Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ , т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра. (слайд)
Заметили, что многие залежи полезных ископаемых тянутся вдоль икосаэдрово-додекаэдровой сетки. Еще более удивительные вещи происходят в местах пересечения этих ребер: тут располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, здесь шотландское озеро Лох-Несс, Бермудский треугольник.
Центры всех магнитных аномалий и магнитного поля планеты расположены в узлах системы треугольников. (слайд) Дальнейшие исследования земли, возможно, подтвердят эти красивые гипотезы, в которой правильные многогранники занимают важное место.
Обобщая все вышесказанное, считаю, что додекаэдр достоин занять место президента многогранников.
ПРЕДСЕДАТЕЛЬ.
Последний момент перед выборами. Вся предвыборная гонка остановлена. Ни какой агитации. Вы решаете свой окончательный выбор.
Проголосуйте за того кандидата, которого вы считаете достойным быть президентом многогранников. На карточках, которые лежат на столе, напишите его название.
Голосование.
СЕКРЕТАРЬ. Пока комиссия подсчитывает голоса, слово независимому эксперту.
НЕЗАВИСИМЫЙ ЭКСПЕРТ
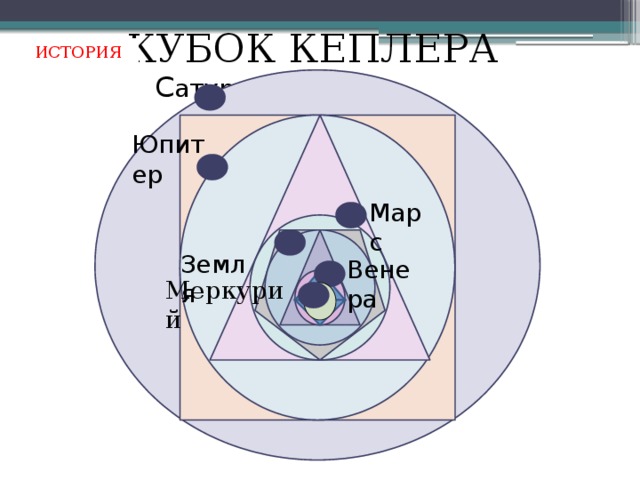
На самом деле, все 5 многогранники очень связаны. Это прозвучало даже в выступлении последнего кандидата. Иоган Кеплер в своей работе «Тайна мироздания» в 1597 году, используя правильные многогранники, вывел, принцип, которому подчиняются формы и размеры орбит планет солнечной системы. (слайд)
Вера в гармонию привела Иоганна Кеплера к озарению: существует 5 Платоновых тел и только 6 планет (известных на то время). Вряд ли это случайно, рассуждал Кеплер, значит, сферы планет связаны между собой вписанными в них Платоновыми телами. Вся модель будет иметь единый центр, которым и будет наше светило Солнце.
Проделав огромную вычислительную работу, испытав сотни вариантов, в 1596г. безызвестный 24-летний учитель Иоганн Кеплер в маленькой книжке «Тайна мироздания» опубликовал формулу своего открытия. В сферу обриты Сатурна он вписывает куб, в куб – сферу Юпитера, в сферу Юпитера – тетраэдр. И так далее последовательно вписываются друг в друга сфера Марса – додекаэдр, сфера Земли – икосаэдр, сфера Венеры – октаэдр.
В едином центре всей системы Кеплер помещает Солнце. Тайна мироздания кажется раскрытой! Вселенная устроена на основе единого геометрического принципа! Ликующий Кеплер мечтает изготовить свою модель Вселенной в виде серебряного кубка. Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы
Сегодня, когда открыты еще 3 планеты, таинственная связь между планетными расстояниями и свойствами правильных многогранников рассыпалась окончательно. Но, эта работа привела к открытию истинных астрономических законов – 3-х знаменитых законов Кеплера, на базе которых Ньютон построил свою теорию тяготения. (слайд)
ПРЕДСЕДАТЕЛЬ: Итак, выборы состоялись. Большинством голосов пост президента многогранников получил…
Преподаватель: Ну, что ж, это наш выбор, хотя спор какой из многогранников важнее, красивее и главнее продолжается веками, единого мнения не существует, а красота этих геометрических тел привлекала и будет привлекать внимание не только математиков, но и поэтов, художников.
5. Итог урока. А наш урок подходит к концу и мы должны подвести итоги.
Какие цели мы ставили перед собой? (слайд)
Выполнили мы поставленные цели?
Цель нашего урока – систематизировать знания о правильных многогранниках, я думаю, что эту цель мы достигли. Мы узнали, какие правильные многогранники существуют, где встречаются в жизни, какое к ним отношение. Давайте еще раз посмотрим на них. (слайд)
Как вы думаете, а существует ли связь между числом вершин, граней, ребер правильного многогранника? Ответ на этот вопрос вы получите, выполнив внеаудиторную работу. Необходимо заполнить таблицу. Если вы правильно посчитаете количество ребер вершин и граней, то подтвердите теорему Эйлера: В+Г-Р=2.
«Когда мы стремимся искать неведомое нам, то становимся лучше, мужественнее и деятельнее тех, кто полагает, будто неизвестное нельзя найти и незачем искать».
Эта мысль Платона должна сопровождать вас на всем жизненном пути. (слайд)
Спасибо всем, активно принявшим участие в подготовке и проведению урока.
(при наличии времени можно показать слайд с полуправильными многогранниками) (слайд)
11