Урок- практикум "Необычный способ получения синусоиды"

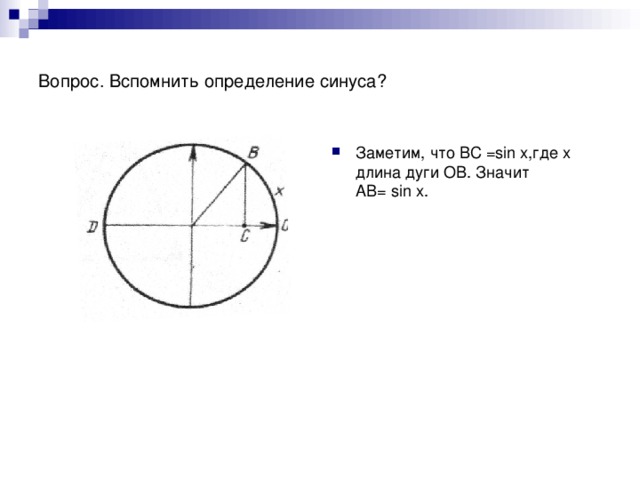
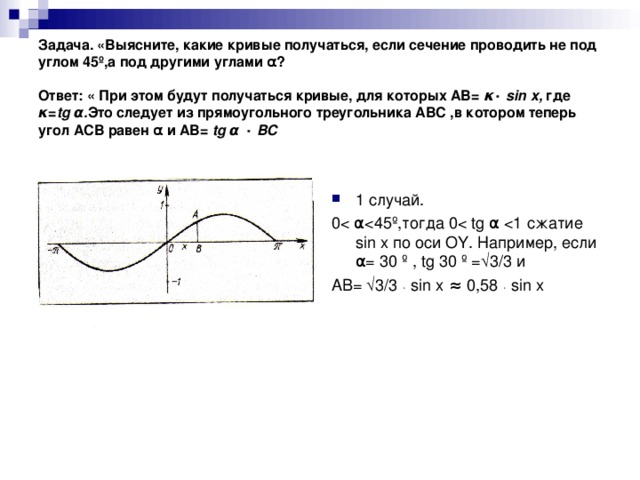
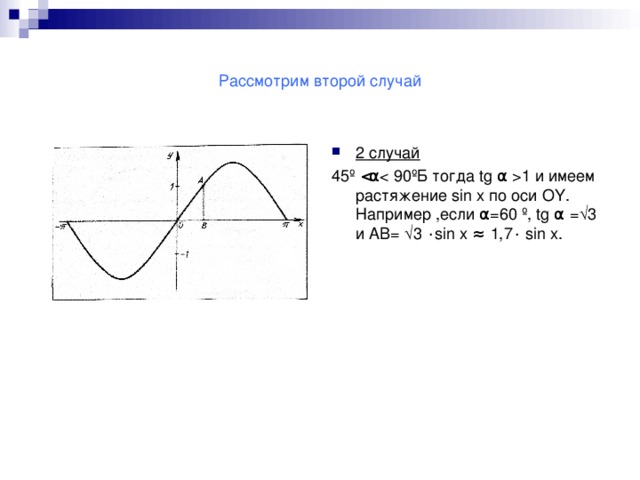
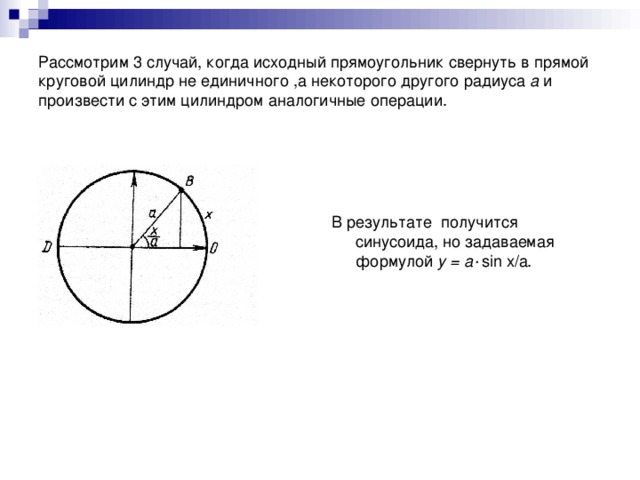
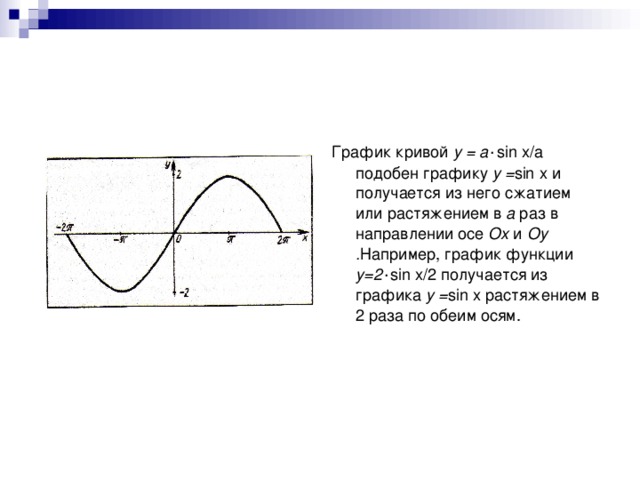
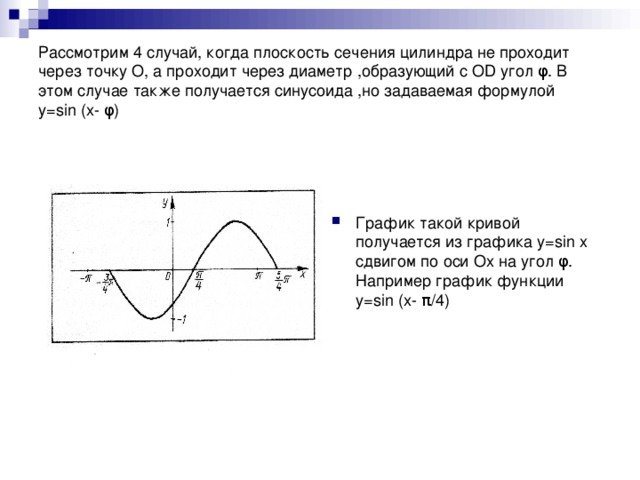
Идея проведения такого урока- практикума не была неожиданной. У ребят старших классов часто наблюдается прагматичное отношение к математике- выучить, слать экзамены,чтобы продолжить обучение в ВУЗе.Поэтому действенным средством воздействия на учеников являются задачи практического содержания,при решении которых возникают проблемные жизненные ситуации,которые можно решить применяя всевозможные решения.Осоое место в усвоении материала по построению графиков функций является необычный спосо построения синусоиды. При построении синусоиды у учащихся возникает вопрос : " Можно ли построить синусоиду другим способом?" В результате был проведен урок- практикум, где было показано получение синусоиды практическим способом,связь математики с другими предметами. Практическое применение данных знаний при изучении других предметов.Задачи урока:на практических примерах расширить возможности учащихся в построении графиков функции; рассмотреть вопрос о преобразовании графиков ( сжатие и растяжение вдоль осей ОХ и ОУ), через решение практических задач показать связь между математикой и физикой.цели обучения:субъективная новизна;направленность на формирование спосоов математической учебной деятельности; направленность на развиие познавательного интереса к математике.рассмотренная задача имеет весьма широкий спектр возможностей. Она наглядна и поэтому хорошо воспринимается и усваивается учащимися.Задачи такого содержания с успехом можно использовать на уроках обобщающего повторения, на внеклассных и факультативных занятиях, при углубленном изучении математики, позволяет осознанно строить графики гармонических колебаний при изучении физики.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Урок- практикум "Необычный способ получения синусоиды"»

Необычный способ получения синусоиды (урок-практикум)

Зотова Ольга Ивановна

МОУ Чикская СОШ №6

Цели и задачи урока:

На практических примерах расширить возможности учащихся в построении графика функции у= sinx .
Рассмотреть вопрос о преобразовании графиков( сжатие и растяжение вдоль осей Ох и Оу)
Через решение практической задачи показать связь между математикой и физикой.

Практическое задание: если обвернуть свечу несколько раз листком бумаги, перерезать свечу наклонным острым ножом или бритвой ,затем разнять обе половинки свечи и, наконец развернуть бумагу, то получится кривая линия, которая называется синусоидой .

Вопрос : «Почему же получившаяся кривая действительно синусоида?»

Проблемная задача ,для решения которой учащимся потребуется знания курса алгебры и геометрии.

математическая модель

Сечение

Возьмем на эллипсе какую-нибудь точку ,например точку А, и опустим перпендикуляры на плоскость окружности и диаметр окружности OD . Получим соответственно точки В и С. Треугольник АВС прямоугольный и равнобедренный, так как угол АВС равен 90 º ,а угол АСВ равен 45 º . Следовательно АВ=ВС.

Вопрос. Вспомнить определение синуса?

Заметим, что ВС = sin x ,где х длина дуги ОВ. Значит АВ= sin x .

Задание: развернуть цилиндр обратно в прямоугольник.

Получили кривую ,для которой АВ= sin x ,где х =ОВ ,т.е.эта кривая является частью синусоиды.

Задача. «Выясните, какие кривые получаться, если сечение проводить не под углом 45 º ,а под другими углами α ? Ответ: « При этом будут получаться кривые, для которых АВ= κ ٠ sin x , где κ = tg α . Это следует из прямоугольного треугольника АВС ,в котором теперь угол АСВ равен α и АВ= tg α ٠ ВС

1 случай.

АВ= √3/3 ٠ sin x ≈ 0,58 ٠ sin x

Рассмотрим второй случай

2 случай

45 º 1 и имеем растяжение sin x по оси OY . Например ,если α =60 º , tg α =√3 и АВ= √3 ٠ sin x ≈ 1,7 ٠ sin x .

Рассмотрим 3 случай, когда исходный прямоугольник свернуть в прямой круговой цилиндр не единичного ,а некоторого другого радиуса а и произвести с этим цилиндром аналогичные операции.

В результате получится синусоида, но задаваемая формулой у = а ٠ sin x/a.

График кривой у = а ٠ sin x/a подобен графику у = sin x и получается из него сжатием или растяжением в а раз в направлении осе Ох и Оу . Например, график функции у=2 ٠ sin x/ 2 получается из графика у = sin x растяжением в 2 раза по обеим осям.

Рассмотрим 4 случай, когда плоскость сечения цилиндра не проходит через точку О, а проходит через диаметр ,образующий с О D угол φ . В этом случае также получается синусоида ,но задаваемая формулой y=sin (x- φ )

График такой кривой получается из графика y=sin x сдвигом по оси Ох на угол φ . Например график функции y=sin (x- π /4 )

Замечание:

Возвращаясь к исходной задаче о свече, заметим, что если учитывать толщину листа бумаги, которая оборачивается вокруг свечи, то цилиндры различных слоев этой бумаги будут иметь разный радиус, увеличивающийся по мере удаления от центра. Следовательно, соответствующие участки синусоиды будут более растянутыми по сравнению с первоначальными. Причем это растяжение будет увеличиваться по мере удаления.

Заключение:

Рассмотренная задача имеет широкий спектр возможностей. Она наглядна и хорошо воспринимается и усваивается учащимися.Такая задача с успехом может быть использована на уроках обобщающего повторения, на факультативных и внеурочных занятиях, при углубленном изучении математики, а также при рассмотрении вопросов по физике связанных с гармоническими колебаниями.