Урок по теме:«Параллельный перенос»

Геометрия, 9 кл.

Величие не в том, чтобы впадать в крайность, но в том, чтобы касаться одновременно двух крайностей и заполнять промежуток между ними.

Блез ПАСКАЛЬ

Тема урока: «Параллельный перенос»

Цель урока: сформировать понятие параллельного переноса как вида движения.

Задачи урока:

• развивать умения использовать свойства движения для решения задач;

• научить выполнять параллельный перенос простейших геометрических фигур;

• Развивать познавательные интересы учащихся через практическое применение параллельного переноса в архитектуре, дизайне, паркетах…

Оборудование: Компьютер, проектор, интерактивная доска.

Ход урока:

1. Орг. момент.

Здравствуйте, садитесь. Приготовьте, пожалуйста, геометрические принадлежности, дневники.

1. Актуализация опорных знаний.

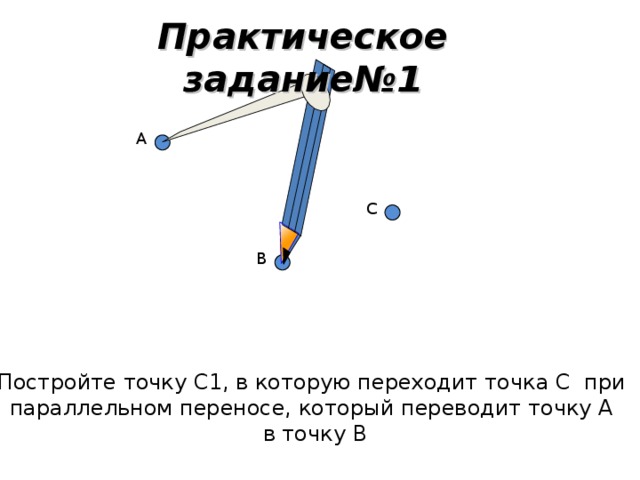
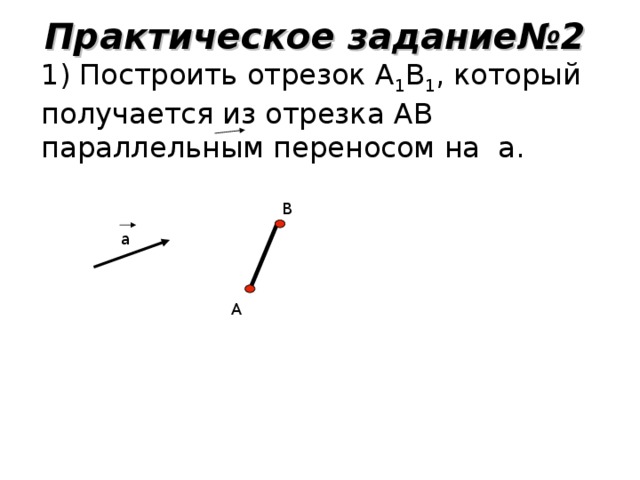
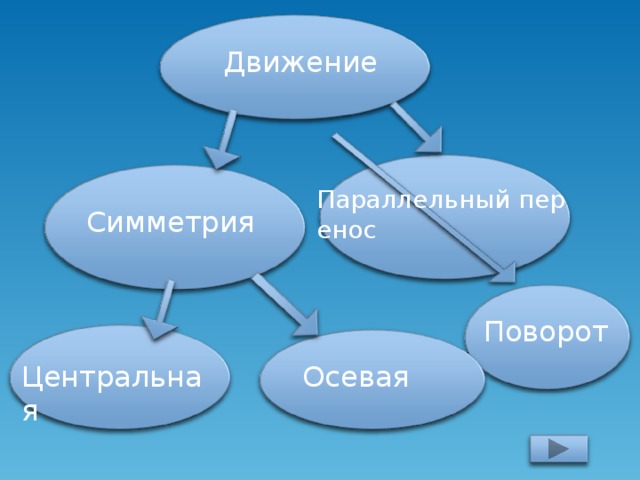
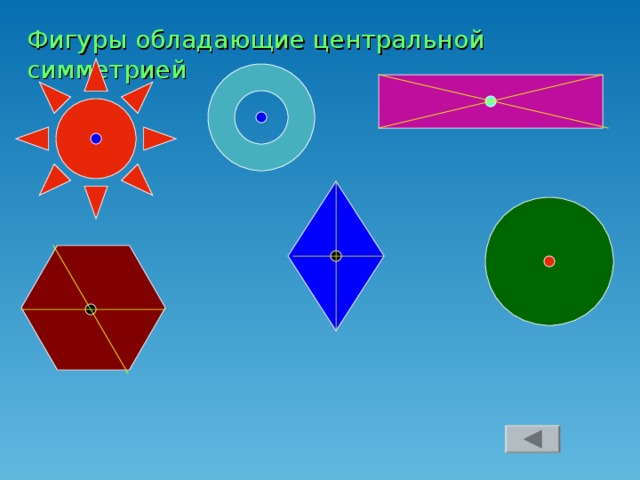
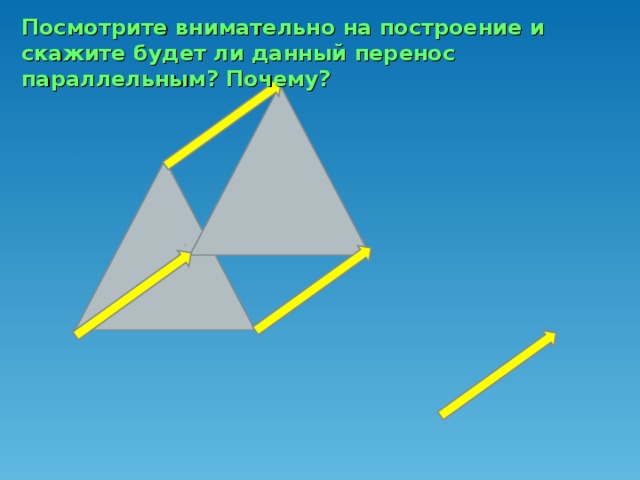
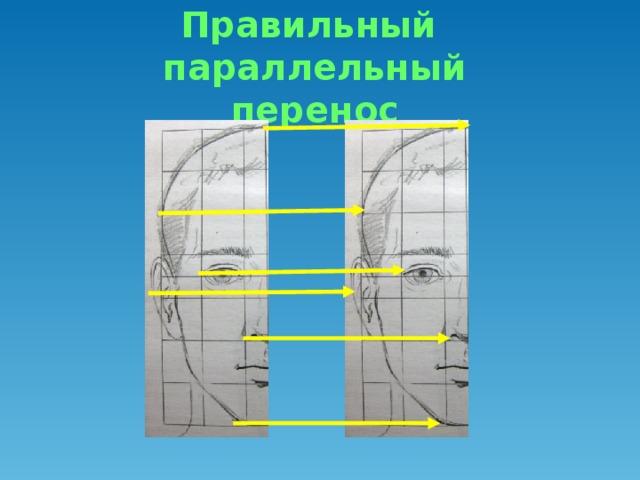
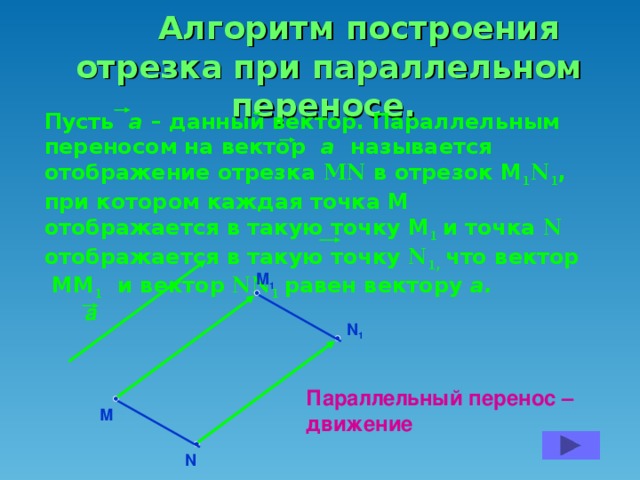
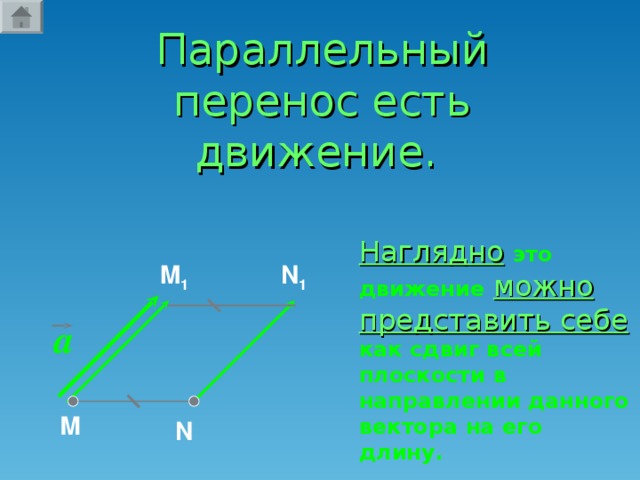
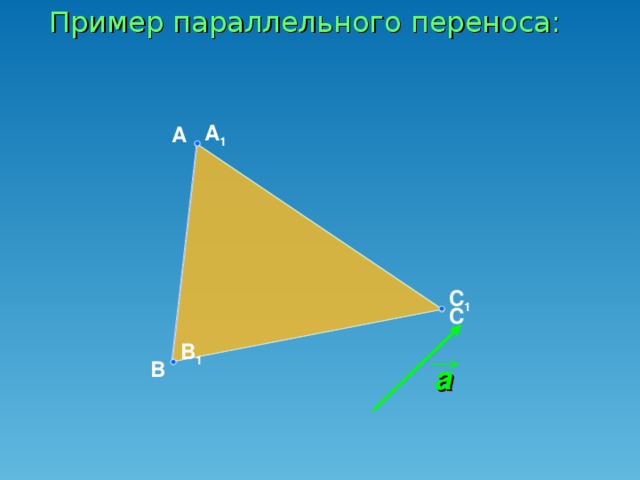
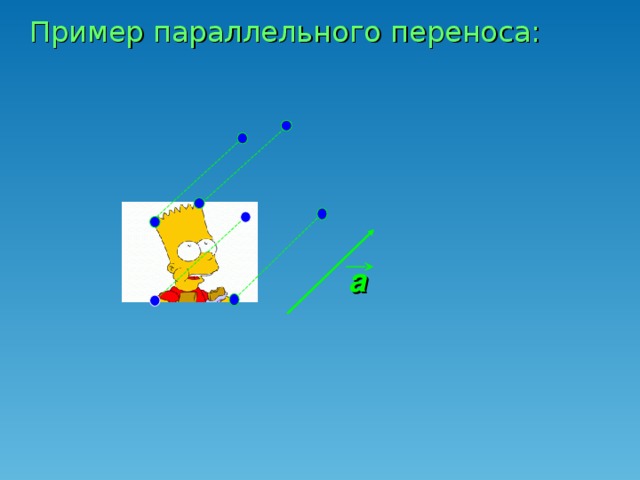
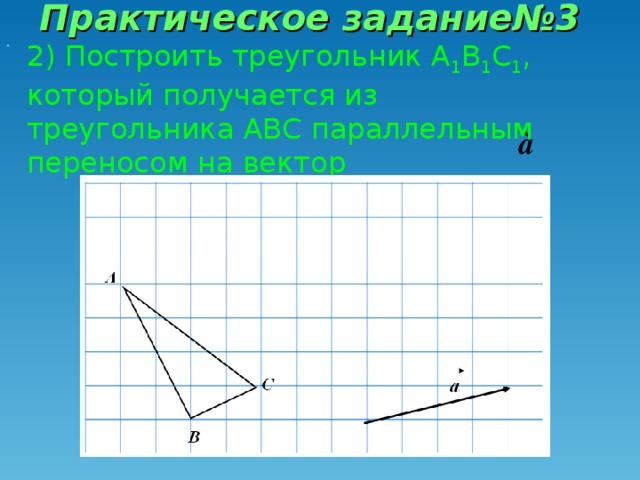
Давайте вспомним, какую главу мы проходим? (Ответ: Движение. Слайд 1). А какой вид движения мы уже рассмотрели? (Ответ: Симметрию). Назовите 2 вида симметрии, известные нам? (Ответ: Центральная и осевая). Вспомним особенности центральной симметрии (Слайд 2,3). Вспомним особенности осевой симметрии (Слайд 4,5,6). Прежде чем перейти к нашей теме нам необходимо вспомнить: Какое отображение плоскости на себя называется движением? (Ответ: Движение, сохраняющее расстояние. Слайд 7). Давайте вспомним свойства движения: (Ответ: Сохраняется расстояние между 2 точками. Отрезок отображается на отрезок. Треугольник отображается на равный ему треугольник. (Слайд 8). Как вы думаете, является ли симметрия единственным видом движения? (Ответ: ……..). Например, если мы сейчас пересадим Безрукову Татьяну с первой парты на последнюю. Какое движение мы совершим? (Ответ: Параллельный перенос. Слайд 1). Наводящий вопрос: А если мы Семечкова Никиту посадим не лицом ко мне, а развернем её на 180 градусов, какое движение мы совершим? (Ответ: Поворот. Слайд 1).

1. Постановка цели и задач урока.

Как вы думаете, что мы сегодня будем изучать на уроке? Какой вид движения мы будем изучать? (Ответ: Параллельный перенос. Слайд 9). Следовательно, из темы урока какую цель и какие задачи мы поставим себе на урок? А как вы думаете, чему мы должны научиться на уроке? (Ответ:……… Слайд 10).

IV. Формирование новых знаний.

Как вы понимаете словосочетание параллельный перенос? (Ответ:………..Слайд 11). Посмотрите внимательно на построение и скажите, будет ли данный перенос параллельным? Почему? (Ответ:…..Слайд 12). Сравните данный слайд с предыдущим. Будет ли данный перенос параллельным? (Ответ:……Слайд 13). Является ли данный перенос параллельным? (Ответ:……Слайд 14,15). Что общего во всех рассмотренных изображениях? (Слайд 16). Давайте рассмотрим алгоритм построения точки при параллельном переносе. (Слайд 17). Давайте рассмотрим алгоритм построения отрезка при параллельном переносе. (Слайд 18). Давайте посмотрим наглядный параллельный перенос отрезка. (Слайд 19). Давайте запишем алгоритм построения при параллельном переносе. (Слайд 20). Обратите внимание на интересную вещь: как движется жесткая фигура при параллельном переносе. (Слайд 21). Рассмотрим алгоритм построения треугольника, который получается из данного треугольника АВС параллельным переносом на вектор а. (Слайд 22). Рассмотрим алгоритм построения четырёхугольника, который получается из данного четырёхугольника АВСD параллельным переносом на вектор а. (Слайд 23).

V. Закрепление знаний.

С параллельным переносом мы часто сталкиваемся в повседневной жизни, например, как можно перенести изображение Барта Симпсона на данный вектор а. (Слайд 24). Как вы думаете, где может использоваться параллельный перенос? (Ответ: в черчении, строении и т.д……..). Давайте посмотрим, как например, используется параллельный перенос в дизайне. (Слайд 25,26,27).

VI. Формирование новых умений.

А теперь переходим к практическим заданиям. (Слайд 28,29,30). Выполняют задания на заранее распечатанных листах (файл карточки.ppt). Два человека вызываются выполнить задание на интерактивной доске. (файл интерактивный пример1.wtz и интерактивный пример2.wtz). Задание: Из предложенных фигур постройте параллельный перенос фигуры на данный вектор.

1. Рефлексия.

Подведём итог урока:

Что нового вы узнали сегодня на уроке? (Ответ: ………..Слайд 31).

Чему вы научились на уроке? (Ответ: ………..).

1. Итог урока, комментирование Д/З:

1. Открываем дневники, записываем домашнее задание №1162(этот номер нужно сделать как слайд номер18 или 19), №1165(этот номер нужно сделать как слайд номер 20 или 22,23).

2. Выставление оценок.

3

Практическое задание№1

А

С

В

Постройте точку С1, в которую переходит точка С при

параллельном переносе, который переводит точку А

в точку В

Практическое задание№2

1) Построить отрезок А 1 В 1 , который получается из отрезка АВ параллельным переносом на а.

В

а

А

Практическое задание№3

2) Построить треугольник А 1 В 1 С 1 , который получается из треугольника АВС параллельным переносом на вектор

.

.

Движение

Параллельный перенос

Симметрия

Поворот

Центральная

Осевая

Центральная симметрия

Центральная симметрия пространства есть движение, поэтому центральная симметрия обладает свойствами, присущими любому движению: прямая переходит в прямую, отрезок - в отрезок, плоскость в плоскость.

Фигуры обладающие центральной симметрией

Осевая симметрия

Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М 1 относительно оси а.

С осевой симметрией мы часто встречаемся в быту, архитектуре, технике, природе.

Осевая симметрия вокруг нас

Какое отображение плоскости на себя называется движением?

Движение, сохраняющее расстояния

Свойства движения:

1. Сохраняется расстояния между 2 точками

2. Отрезок отображается на отрезок

3. Треугольник отображается на равный ему треугольник

Цель урока: сформировать понятие параллельного переноса как вида движения.

Задачи урока:

• Развивать умения использовать свойства движения для решения задач;
• Научить выполнять параллельный перенос простейших геометрических фигур.
• Развивать познавательные интересы учащихся через практическое применение параллельного переноса в архитектуре, дизайне, паркетах…

Посмотрите внимательно на построение и скажите будет ли данный перенос параллельным? Почему?

Сравните данный слайд с предыдущим. Будет ли данный перенос параллельным?

Является ли данный перенос параллельным?

Правильный параллельный перенос

Вывод:

• Параллельный перенос является движением;
• Сохраняется расстояние между 2 точками;
• Имеется направленный вектор переноса.

Алгоритм построения точки при параллельном переносе.

Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М 1 , что вектор М М 1 равен вектору а .

М 1

а

М

М

Алгоритм построения отрезка при параллельном переносе.

Пусть а – данный вектор. Параллельным переносом на вектор а называется отображение отрезка MN в отрезок М 1 N 1 , при котором каждая точка М отображается в такую точку М 1 и точка N отображается в такую точку N 1, что вектор ММ 1 и вектор NN 1 равен вектору а.

M 1

а

N 1

Параллельный перенос –движение

М

N

Параллельный перенос есть движение.

Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

M 1

N 1

a

М

N

C

B

A

D

Алгоритм построения при параллельном переносе.

Х1

• Определяется: вектором.
• Обозначение:
• Построение:

1) Х- произвольная точка.

2) Строим прямую а∥ .

3) Откладываем ХХ1= .

(ABCD)=A1B1C1D1.

Х

а

C 1

B 1

Построение 4-х угольника

D 1

A 1

Пример параллельного переноса:

A 1

А

C 1

С

B 1

В

a

Построить четырёхугольник, который получается из данного четырёхугольника АВС D параллельным переносом на а

С

В

а

С 1

В 1

D

А

D 1

А 1

Параллельный перенос –

движение.

Пример параллельного переноса:

a

Параллельный перенос, используемый в дизайне

Параллельный перенос.

24

Параллельный перенос

24

М. Эшер. «Рыба, заглатывающая корабль». Параллельный перенос.

Практическое задание №1

А

С

В

С 1

Постройте точку С1, в которую переходит точка С при

параллельном переносе, который переводит точку А

в точку В

Практическое задание№2

1) Построить отрезок А 1 В 1 , который получается из отрезка АВ параллельным переносом на а.

а

В

А

Практическое задание№3

2) Построить треугольник А 1 В 1 С 1 , который получается из треугольника АВС параллельным переносом на вектор

.

.

Практическое задание на интерактивной доске:

1) интерактивный пример1.wtz

2) интерактивный пример2.wtz

Подведем итоги

• Параллельный перенос является движением
• Сохраняется расстояние между 2 точками
• Направление заданного вектора переноса

Домашнее задание№1162,№1165

• Задание №1162
• Задание №1165