Тема "Производная" является одной из важнейших тем математического анализа. Знание этой темы способствует освоению темы "Интеграл" в 11 классе.Умение исследовать функции тоже опирается на знания по теме " Производная". Поэтому очень важно, чтобы сложные элементы математического анализа были доступны для понимания учащихся. Поэтому применение игровых элементов на уроке делает материал более занимательным и понятным. Игра состоит из нескольких этапов на каждом этапе в групповой форме происходит закрепление изученного материала.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок-игра " Восхождение на пик производной"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок-игра " Восхождение на пик производной"»
Полезное для учителя
Распродажа видеоуроков!
1900 руб.
2710 руб.
1970 руб.
2820 руб.
2100 руб.
3000 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
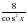
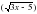 / =
/ =
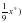 / =х8
/ =х8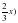 / =0
/ =0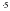 5
5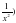 / =
/ = 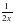

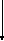 3. y
3. y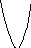
 x
x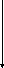 4 y
4 y
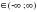
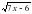 равна:
равна: й)
й) п)
п)  ю)
ю)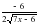

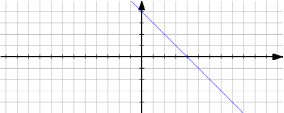
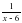
 ц) (-
ц) (- я) (6;
я) (6; ф)(-
ф)(-