| Урок алгебры в 8-м классе по теме "Вынесение множителя из-под знака корня. Внесение множителя под знак корня"
Цели: 1. Начать формировать умение учащихся выносить множитель из-под знака корня и вносить множитель под знак корня на простейших примерах. 2. Развивать и совершенствовать умения применять имеющиеся у учащихся знания в измененной ситуации, развивать логическое мышление, умение делать вывод и обобщения. 3. Воспитывать интерес к предмету, культуру поведения, чувство ответственности. Тип: изучение нового материала. Форма: игровая, исследовательская работа(ознакомление с этапами исследовательской работы). Оборудование: оформленная доска, эмблема,плакат с заданием, алгоритмы. ХОД УРОКА 1. Организационный момент. Взаимное приветствие. 2. Устно. 1) Какие из следующих равенств являются верными? 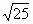 =5, - =5, - 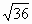 = - 6, = - 6, 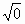 = - 0, = - 0, 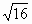 =-4, =-4, 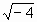 = - 2, = - 2, 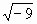 =3. =3. 2) Представьте числа в виде произведения таких множителей, чтобы один из них являлся квадратом рационального числа. 125= 363= 108= 845= 3) Представьте числа в виде арифметического корня: 3, 11, 4, 15, 2. 4) Вычислите значение выражения 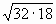 = = 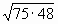 = = 5) На смекалку. Продолжи ряд чисел: 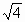 , , 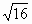 , , 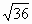 , … , … 3. Изучение нового материала. Итак, ребята, перед нами практическая задача:Применим теорему о корне из произведения. Как сравнить значения выражений? 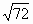 и 4 и 4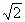 а) Для 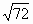 применим теорему о корне из произведения. применим теорему о корне из произведения. б) представим произведение 4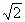 в виде арифметического квадратного корня. в виде арифметического квадратного корня. Такие преобразования называют вынесение множителя из-под знака корня и внесение множителя под знак корня. Данная тема очень часто применяется для сравнения выражений и преобразовании выражений,содержащих квадратные корни. Прежде чем приступить к данной теме на практике, давайте составим алгоритм вынесения множителя из-под знака корня и внесение множителя под знак корня. (Вывешивается последовательно на доску) ВЫНЕСЕНИЕ МНОЖИТЕЛЯ ИЗ-ПОД ЗНАКА КОРНЯ 1) Представим подкоренное выражение в виде произведения таких множителей, чтобы из одного можно было бы извлечь квадратный корень. 2) Применим теорему о корне из произведения. 3) Извлечь корень Пример. 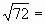  Запишем данное преобразование и в буквенном виде: Если а ВНЕСЕНИЕ МНОЖИТЕЛЯ ПОД ЗНАК КОРНЯ 1) Представим произведение в виде арифметического квадратного корня. 2) Преобразуем произведение квадратных корней в квадратный корень из произведения подкоренных выражений.. 3) Выполним умножение под знаком корня. Пример.  Запишем данное преобразование в буквенном виде: Если  4. А теперь ребята, давайте обратим внимание на этапы исследовательской работы и переходим к следующему этапу – применение наших исследований на практике. № 401 (б, г, е, з) б) (на доске и в тетрадях) (на доске и в тетрадях) г) (прокомментировать с места) (прокомментировать с места) е)  (вернуться к устным упражнениям №2) (вернуться к устным упражнениям №2) з) (вернуться к устным упражнениям №2) (вернуться к устным упражнениям №2) № 401 (а, в) 2 ученика на крыльях доски а) 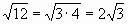 б) 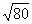 = =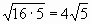 № 401 ( д, ж) - прокомментировать № 404 (в, г) (на доске и в тетрадях) в) 5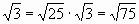 г) 10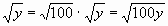 № 404 (а, б) - 2 ученика на крыльях доски а) 7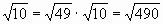 б) 6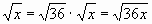 5. Я считаю, что у вас хорошие результаты исследовательской работы и теперь каждый оценит себя сам при выполнении обучающего теста. Обучающий тест. Ф.И._____________________ Вынести множитель из-под знака корня: 1) 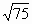 = = а) 3 , б) 5 , б) 5 , в)-5 , в)-5 , г) -3 , г) -3 . . 2) 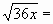 а) 6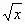 , б) –x , б) –x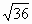 , в) -6 , в) -6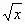 , г) x , г) x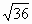 . . 3) = = а) 6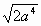 ; б)6а ; б)6а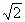 ; в)6а2 ; в)6а2 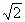 ; г)-6а ; г)-6а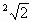 . . Внести множитель под знак корня: 4) 6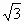 = = а) 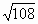 , б) , б) 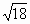 , в) - , в) -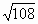 , г) , г) 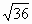 . . 5) 5 = = а)  , б) , б)  , в) - , в) - , г) , г)  . . Каждое правильно выполненное задание оценим в 1балл. Кто набрал 3 балла? Более 3 баллов? Более 4баллов? Оценки все кроме “2” в журнал, “3” по желанию. Те, у кого были затруднения на перемене подойти к доске и просмотреть решения заданий. 6. Ребята наша исследовательская работа на сегодняшнем уроке не заканчивается.Поэтому дома продолжаете работу с п.17, обращаете особое внимание на примеры выражений, содержащих переменную перед радикалом и под радикалом. О результатах своих исследований сообщите на следующем уроке и не забывайте об этапах исследовательской работы. В дневниках записали:п.17 № 403, № 407. 7. За вашу сегодняшнюю работу предлагаю вам басню на размышление: 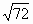 ( ( ) )  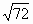 (?) (?)  Указание: разобраться в закономерности чисел, расположенных в 1 строке и учитывая эту закономерность по аналогии вместо ? поставить выражение. Спасибо за урок. Урок окончен. | 















