Урок алгебры и начала анализа в 12 классе вечерней школы Тема урока: Дифференцирование показательной функции

Урок алгебры и начала анализа в 12 классе вечерней школы

Тема урока: Дифференцирование показательной функции

Цели урока: Рассмотреть наиболее типичные примеры применения вычисления производной показательной функции .

Задачи:

-образовательные: Сформировать умение вычисления производных показательной функции;

-развивающие: Научиться решать задачи на исследование функций, составление уравнения касательной.

-воспитывающие: воспитание познавательного интереса к учебному предмету.

Оборудование: мультимедийная аппаратура, презентация, раздаточный материал, справочный материал.

Ход урока.

І. Организационный момент

Сегодня на уроке, мы рассмотрим типичные примеры вычисления производной и применения её к решению задач.

ІІ. Актуализация опорных знаний.

1. Проверка домашнего задания (слайд ) ( приготовили ученики) №538

(Ответы на вопросы по домашнему заданию).

1. Устная работа с целью систематизировать теоретические сведения, связанные с вычислением производной и первообразной функции.

Найдите производную функции.(Слайд1)

а) y = 3x² + 11; б) y = ; в) y = cos 3x;

г) y = 3e^x; д) y = ; е) y = 3 ln x + sin 2x;

ж) y = ln x + x; з) ln (2x + 2).

ІІІ. Решение задач с целью совершенствовать умения применять знание к вычислению производных и расширить кругозор при выполнении творческих заданий.

1. Выполнить упражнение на доске №539 (б, г).

2. Работа в группах (взаимопроверка):

1 группа № 541(а,б).

2 группа №541(в, г).

1. На примере 3 со с. 253 учебника вспоминаем с учащимися алгоритм решение задач на исследование функций

2. Решить задачу ( комментирование).

Исследуйте на возрастание( убывание ) функцию: у= 2 ln x³ – 5x +

у= 2 ln x³ – 5x + ; D (f) = (0; +);

y' = 2 · 3x² · – 5 + · 2x = + x – 5;

y' = 0, если + x – 5 = 0; = 0;

x² – 5x + 6 = 0;

x₁ = 2; x₂ = 3.

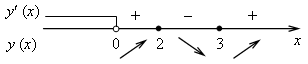
Имеем, функция возрастает на (0; 2] и на [3; +); убывает на [2; 3].

Проверить решение на слайде.

1. Самостоятельное решение.

Исследуйте на возрастание( убывание ) функцию y = x²e^x ( слайд);

Проверка решения демонстрируется на слайде.

y = x²e^x; y' = 2xe^x + x²e^x = e^x (x² + 2x);

y' = 0 если x² + 2x = 0;

x (x + 2) = 0;

х = 0 или х = –2.

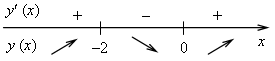
Функция y = x²e^x монотонно возрастает на (–∞; –2] u [0; +∞) и монотонно убывает на [–2; 0].

1. Вспоминаем с учащимися алгоритм решения задач на составление уравнения касательной к графику функции в точке х₀ = а:

y = f (a) + f ' (a) · (x – a)

Алгоритм (на слайде)

1. Найти производную ;

2. Найти производную в точке х₀

3. Значение функции в точке х₀

4. Подставить в формулу.

6) Решение задач№540(в) ( Проверка решения демонстрируется на слайде):

Составьте уравнение касательной к графику функции y =е^x в точке с абсциссой х₀ =0

1) y = e^x ; y' = e^x

2) y'(0) = е⁰ =1

3) y (0)= е⁰ =1

4) у = 1 ( х- 0 ) +1 = х+1.

Ответ: у = х+1.

Дополнительно: Задания творческого плана №542(б)

ІV. Домашняя контрольная работа.

Вариант 1

1. Найдите производную функции.

а) y = 2e^x + cos 3x;

б) y = e^{2x – 5} ;

2. Составьте уравнение касательной к графику функции y =3 + e^{x – 1} в точке с абсциссой, равной 1.

Вариант 2

1. Найдите производную функции.

а) y = 3e^x – sin 2x;

б) y = e^{2 – x};

2. Составьте уравнение касательной к графику функции y = 5 – e^{x + 3} в точке с абсциссой, равной –3.

V. Итоги урока.

Оценки за урок. При решении каких заданий нам нужны знания производной

Достигли ли мы поставленной цели на уроке?

-Чему научились? Что узнали нового?

Работали все хорошо - молодцы.

Домашнее задание: № 540 (а; г), №539 (в; г), № 542, повторить п.41.