Графикпен таныстыру. Логикалық ойлау қабілетін дамыту
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
У=ах2+вх+с функциясының графигі
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«У=ах2+вх+с функциясының графигі»
Полезное для учителя
Распродажа видеоуроков!
1730 руб.
2880 руб.
1900 руб.
3170 руб.
1490 руб.
2480 руб.
1060 руб.
1760 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
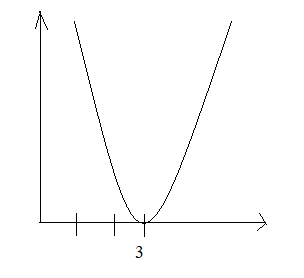
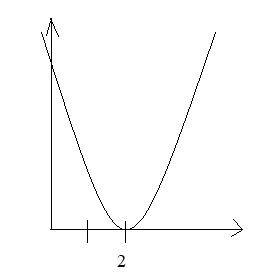
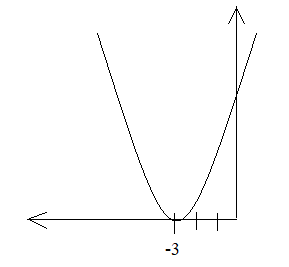
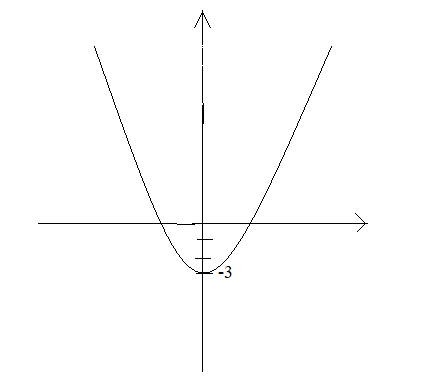
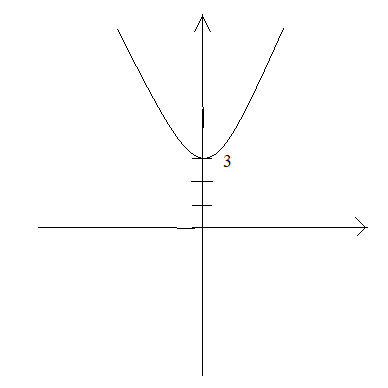
 0 болғанда m бірлікке оңға, немесе m
0 болғанда m бірлікке оңға, немесе m  0 болғанда │ m│ бірлікке солға және Оу осі бойымен n˃0 болғанда
0 болғанда │ m│ бірлікке солға және Оу осі бойымен n˃0 болғанда 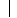 n
n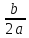 )2-
)2-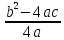
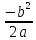 n=
n=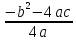
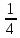

 Оқушылар және фигураларын таңдап екі команадаға бөлінеді. Ойында шабуылшылар, қорғаушылар, қақпашы болады. Алдымен екі команданың шабуылшылары ойыныды бастайды. Бірдей есептер шығарады. Кім жылдам шығарады сол екінші команданыі қорғаушысымен ойнайды т.с.с. Қақпашыны жеңген команда ұпай алады.
Оқушылар және фигураларын таңдап екі команадаға бөлінеді. Ойында шабуылшылар, қорғаушылар, қақпашы болады. Алдымен екі команданың шабуылшылары ойыныды бастайды. Бірдей есептер шығарады. Кім жылдам шығарады сол екінші команданыі қорғаушысымен ойнайды т.с.с. Қақпашыны жеңген команда ұпай алады.















