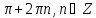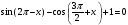.
| Мектеп: Базылбек Ахметов атындағы орта мектеп КММ Мұғалім: Нургазинова Д. А. |
| Күн: 17.11. 2017 | Сынып: 10а Пән: алгебра және талдау бастамалары |
| Тақырыбы | Тригонометриялық теңдеулерді шешу |
| Мақсаты | Білімділік: Тригонометриялық теңдеулерді шешудің әртүрлі тәсілдерін қолдануға есептер шығарту, теориялық білімдерін практикада қолдана білу бейімділіктерін қалыптастыру. Дамытушылық: Қарапайым тригонометриялық теңдеулерді шешу алгоритмін, тригонометриялық формулаларды теңдеулерді шешуде қолдану дағдыларын дамыту. Тәрбиелік: Өз ойын ашық жеткізуге, өзгенің пікірімен санасуға баулу, пәнге қызығушылығын арттыру. |
| Сабақ түрі | Есептер шығарту сабағы |
| Кезеңі | Мұғалім әрекеті | Оқушылар әрекеті |
| 7 | Сәлемдесу, түгендеу |
|
| Қайталау- оқу анасы | -Тригонометриялық теңдеу...
-Қарапайым тригонометриялық теңдеулер ...
-Тригонометриялық теңдеулерді шешу... | Айнымалысы тригонометриялық функция таңбасының ішінде болатын теңдеу тригонометриялық теңдеу деп аталады. Sinx=a, Cosx=a, tqx=a, ctqx=a түріндегі теңдеулер қарапайым тригонометриялық теңдеулер деп аталады. шешу Тригонометриялық теңдеулерді шешу теңдеуді тура теңдікке айналдыратын аргументтің барлық мәндерін анықтау |
| Ойлан тап! | Қарапайым тригонометриялық теңдеулерді шешу Топтық жұмыс |
| І топ | 1. 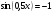 2. 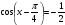 3. 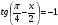 4. 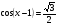 5. 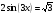 | 1. 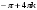 2. 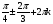 3. 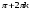 4. 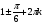 5. 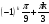 |
| ІІ топ | 1. 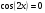 2. 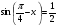 3. 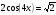 4. 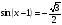 5. 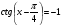 | 1. 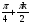 2. 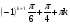 3. 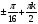 4. 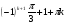 5. 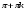 |
| Жеке жұмыс
Тақтада орындау | Тригонометриялық теңдеулерді шешу әдістерін анықтап, теңдеулерді шеш |
| sin2x - 3sinx cosx + 2cos2x = 0 | Біртектес тригонометриялық теңдеу tg2 x-3tgx+2=0 1)tgx=1 2) tgx= 2 x=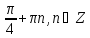 x=arctg2+ x=arctg2+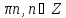 |
| sіnх+ sіn2х + sіn3х = 0 | Формуланы қолдану 2sin2xcosx+sin2x=0 Sin2x(2cosx+1)=0 1)Sin2x=0 2) cosx =-0,5 2x=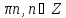 x= x=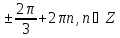 x=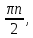 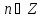 |
| 2sin2x=1- cosx | Алгебралық теңдеулерге келтірілетін теңдеулер 2sin2x=1- cosx 2-2cos2 x+ cosx-1=0 2cos2 x- cosx-1=0 cosx=1 cosx=-0,5 x=2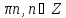 x= x=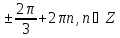 |
| Сұрақ менен, жауап сенен | Қолданылатын формулаларды қайталау, қарапайым тригонометриялық теңдеулерді шешу , тригонометриялық теңдеулерді шешу алгоритмін , дербес жағдайларды еске түсіру |
| Жұптық жұмыс (кітаппен жұмыс) Әр жұп берілген есептерді талдап шығарады
| 6cos2x - 2sіn2x = 1
| 6cos2x - 4sіnxcosx-sin2 x- cos2x = 0 5cos2x - 4sіnxcosx-sin2 x = 0 tg2 x+4tgx-5=0 1)tgx=1 2) tgx=-5 x=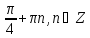 , nZ; arctg5 + n, nZ. , nZ; arctg5 + n, nZ. |
| 3sinx+ cos2x=2 | 2sin2 x-3sinx+1=0 2t2 -3t+1=0 sinx=1 sinx=0,5 x=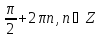 x=(-1)n x=(-1)n 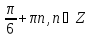 |
| 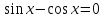 | tgx=1 x=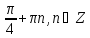 |
| Cos2x=4sinx-5 | sin2 x+2sinx-3=0 t2 +2t-3=0 sinx=1 sinx=-3 x=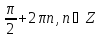 түбірі жоқ түбірі жоқ |
| Cos5x+cos2x+cos3x+cos4x=0 | 2cos4xcosx+2cos3xcosx=0 2cosx(cos4x+cos3x)=0 4cosxcos3,5xcos0,5x=0 cosx=0 cos3,5x =0 cos0,5x=0 x=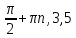 x= x=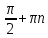 , 0,5x= , 0,5x=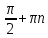 ,n ,n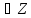 x=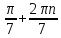 x= x=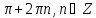 |
|
| 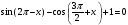
| -sinx-sinx+1=0 2sinx=1 sinx=0,5 x=(-1)n 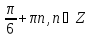 |
| Үйге тапсырма | 82 бет 15-23 тестер | Күнделікке жазу |
| Кері байланыс Екі жұлдыз, бір тілек | Алма түріндегі стикерлерді таратады | Әр оқушы сабақтағы өз деңгейін бағалайды, жеміс ағашына іледі. |
| Оқушы ойларын ескере отырып, сабақтағы оқушы жұмыстарын бағалау |
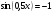
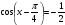
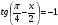
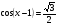
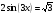
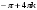
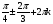
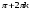
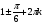
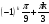
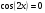
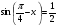
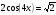
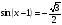
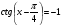
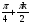
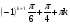
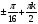
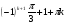
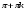
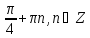 x=arctg2+
x=arctg2+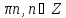
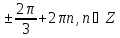
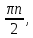
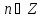
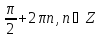 x=(-1)n
x=(-1)n 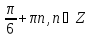
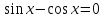
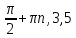 x=
x=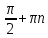 , 0,5x=
, 0,5x=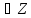
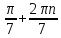 x=
x=