Сабақ тақырыбы: Тригонометриялық функциялардың туындысы
Сабақтың мақсаты:
- Біліармділік: Тригонометриялық функциялардың туындысын есептейтін елерін есептер формулаларға және туындыны табу ережелерін есептер шығаруға қолдану, білік дағдыларын қалыптастыру;
- Дамытушылық: Оқушылардың ой өрісін дамыту, тригонометриялық функциялардың туындысын таба білуге қабілетін дамыту;
- Тәрбиелік: Оқушыларды ұқыптылыққа өз бетінше еңбек етуге, ізденуге баули отырып, жауапкершілікті сезінуге, адамгершілікке баулу, шығармашылыққа тәрбиелеу.
Сабақ әдісі: Деңгейлеп оқыту
Сабақ түрі: Іскерлік пен дағдыны қалыптастыру
Көрнекілігі: оқулық, тест, кестелер
Сабақ барысы: І Ұйымдастыру. Сынып оқушыларымерн сәлемдесу, түгендеу.
Сабаққа дайындықтарын тексеру.
ІІ Үй тапсырмасын тексеру
228
ІІІ Негізгі бөлім
- Сұрақ – жауап
а) Тригонометриялық функциялардың туындылары неге тең?
ә) Туындыны табу ережелерін ата?
б) Күрделі тригонометриялық функциялардың туындысы неге тең?
2. Алгоритмдік деңгей. Деңгейлік тапсырмаларды оқушылар өз таңдаулары бойынша алады.
«А»
- Туындыны табыңдар: f(x) = 4x - sinx
- Туындыны табыңдар: f(x) = cosx2
- f(x)= tgx Функцияның графигінe x= нүктесінде жүргізілген жанаманың көлбеулік бұрышының тангенісін тап.
«В»
- Туындыны табыңдар:
- f(x) Функцияның графигіне x0 нүктесінде жүргізілген жанаманың теңдеуін жаз.
«С»
- Туындыны табыңдар:
- f ´(x) = 0 Теңдеуін шеш. f(x) = sin2x – sinx + 5
3.Қызығушылық деңгей
«А» Тест- сұрақ. Туындыны тап
- f(x) = sinx + x5
- f(x) = tgx + 5
- f(x) = 3x – cosx
- f(x) = 5x2 – ctgx
«В» Сәйкестікті тап
1
(sin3x)´ =
1
2
(4tgx)´ =
2
3x2cosx3
3
(3x4)´=
3
4
(cos2x)´ =
4
3cosx
5
(ctg5x)´ =
5
12x3
6
(sinx3)´=
6
-sin2x
\
«С» «Ойлан тап»
Қ/с
Туындының мәні
Функциялар
1
3/ cos23x
2
-5sin5x
3
-1/ sin2x +3x2
4
2xcosx2
5
5x4sinx5
6
7
8
- Шығармашылық деңгей
Туындыны тап:
Туындының мәнін тап: f ´()
Туындыны тап: f(x) = tgxsin2x
V Оқушыларды бағалау
VI Үйге тапсырма беру
«Ойын» жұбыңды тап:
- ´ = cosx (sinu)´=u´ cosu
(cosx)´ = -sinx (cosu)´ = - u´ sinu
(tgx) ´ = 1/ cos2x (tgu) ´ = u´/cos2u
- ´= - 1/ sin2x (ctgu)´ = - u´/ sin2u
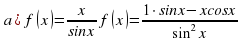
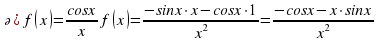

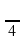 нүктесінде жүргізілген жанаманың көлбеулік бұрышының тангенісін тап.
нүктесінде жүргізілген жанаманың көлбеулік бұрышының тангенісін тап.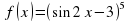
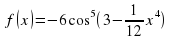
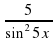
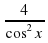
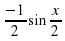
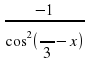
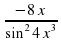
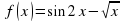
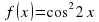 f ´(
f ´(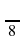 )
)















