"To`g`ri burchakli uchburchakning tenglik alomatlari"

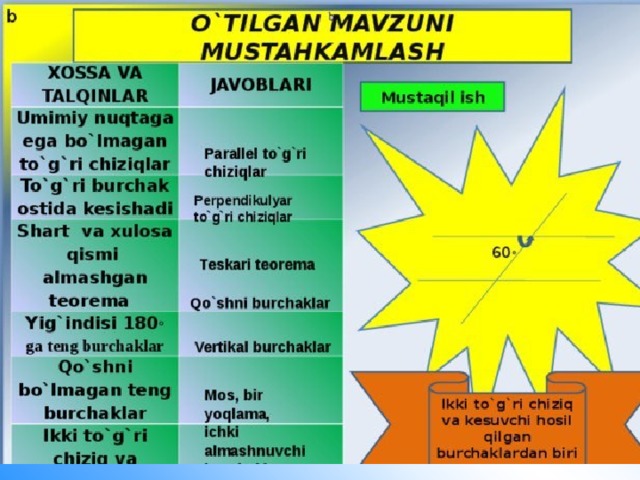
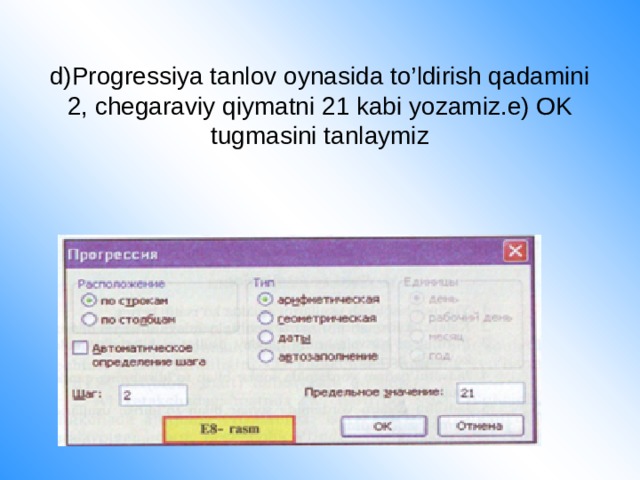
Teorema: Uchburchakning istalgan bir tomoni qolgan ikki tomoni yig’indisidan kichik.
∆ABC, AC<AB+AC.
Isbot: AB to’g’ri chiziqda BC kesmaga teng BD kesmani qo’yamiz va C va D nuqtalarni tutashtiramiz. Natijada BCD teng yonli ∆ hosil bo’ladi. Unda Ð1=Ð2. Chunki, BC=BD. ÐACD>Ð1. U holda ÐACD>Ð2 chunlki Ð1=Ð2. Bu burchaklar ACD uchburchakka tegishli. Katta burchak qarshisida katta tomon yotishini hisobga olsak, AC<AD. U holda, AC<AB+BD. AD=AB+BD. Bundan BD=BC. AC<AB+BC ekanligini hosil qilamiz.
Teorema isbotlandi.
Bu teoremadan quyidagi natija kelib chiqadi.
Natija: Bir to’g’ri chiziqda yotmagan ihtiyoriy uchta A,B va C nuqta uchun AC<AB+BC, AB<AC+BC, BC<AB+AC tengsizlikllar o’rinli.
Bu tengsizliklarning har biri uchburchak tengsizligi deyiladi.
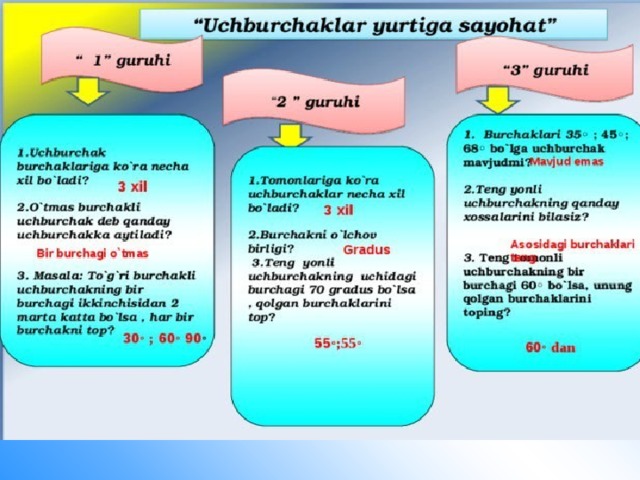
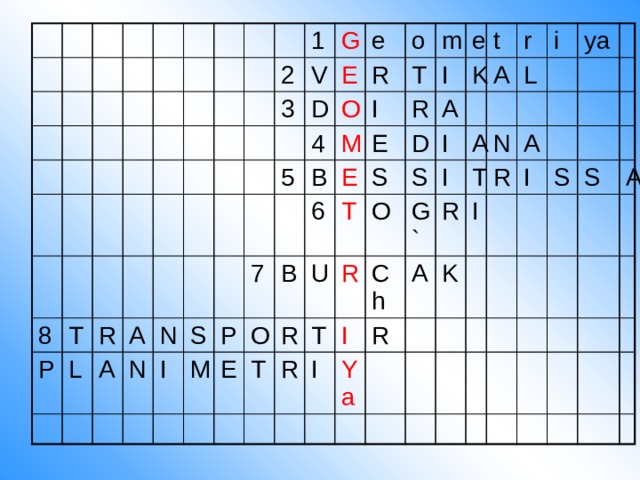
1-masala. 2-rasmda berilgan ma’lumotlardan foydalanib, Ð1>Ð3 ekanligini isbotlang
Yechish:
Ð2>Ð3, Ð2-∆BDCning tashqi burchagi. Tashqi burchak xossasiga ko’ra, Ð2=Ð3+Ð4 va Ð4>0. ∆ACD teng yonli. Ð1=Ð2. Demak, Ð1>Ð3.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«"To`g`ri burchakli uchburchakning tenglik alomatlari"»

O’zbekiston Respublikasi Xalq ta’limi vazirligi

Kattaqo`rg`on tuman 37 -umumiy o’rta ta’lim maktabining

matematika fani o’qituvchisi

Xakimova Feruza Kuvandikovnaning

7- “A”-sinf uchun

ochiq

dars

ishlanmasi

Darsning mavzusi:

To`g`ri burchakli

uchburchakning

tenglik alomatlari

Dars shiori

Kuch –bilim va tafakkurda

Tarbiyaviy

Ta'limiy

Rivojlantiruvchi

o’quvchilarga to`g`ri

burchakli

uchburchak xossalari

bilan ishlash

bo’yicha

bilim ko’nikmalar

berish .

o’quvchilarni yangi

bilimlar

egallashga

va tartib-intizomga

doimo rioya etishga

yo’naltirish

O’quvchilarning ongini ,

diqqatini tarbiyalash

O’quvchilarning

geometriya

faniga qiziqishini oshirish

o’quvchilarning

ichida guruhlarda

ishlash orqali

o’z fikrlarini erkin

bayon etish

xususiyatlarini

rivojlantirish.

Darsda

foydalanila

digan

metodlar

Darsning

jihozi

Dars turi

yangi bilimlarni o’zlashtirish, mustahkamlash hamda takomillashtirish darsi

Kompyuter,

og’zaki, suhbat,

Videoproyektor,

savol-javob,

guruhlarda

tarqatma

ishlash,

materiallar,

taqdimot – slayd

slaydlar,

usuli,

boshqotirma

Darsning blok chizmasi

Dars bosqichlari

Tashkiliy qism

Vaqt

Usullar

O’tilganlarni takrorlash

5 daqiqa

Yangi mavzu ustida ishlash

7 daqiqa

Sj,k,bst

17 daqiqa

Yangi maxzuni mustahkamlash

Ah,m

Uyga vazifa

15 daqiqa

Sj,k,Bst,m

1daqiqa

Yangi mavzu bayoni

 1. U holda  ACD  2 chunlki  1=  2. Bu burchaklar ACD uchburchakka tegishli. Katta burchak qarshisida katta tomon yotishini hisobga olsak, AC Teorema isbotlandi. Bu teoremadan quyidagi natija kelib chiqadi. Natija: Bir to’g’ri chiziqda yotmagan ihtiyoriy uchta A,B va C nuqta uchun AC Bu tengsizliklarning har biri uchburchak tengsizligi deyiladi. 1-masala. 2-rasmda berilgan ma’lumotlardan foydalanib,  1  3 ekanligini isbotlang Yechish:  2  3,  2-∆BDCning tashqi burchagi. Tashqi burchak xossasiga ko’ra,  2=  3+  4 va  40. ∆ACD teng yonli.  1=  2. Demak,  1  3." width="640"

Teorema: Uchburchakning istalgan bir tomoni qolgan ikki tomoni yig’indisidan kichik. ∆ABC, AC Isbot: AB to’g’ri chiziqda BC kesmaga teng BD kesmani qo’yamiz va C va D nuqtalarni tutashtiramiz. Natijada BCD teng yonli ∆ hosil bo’ladi. Unda  1=  2. Chunki, BC=BD.  ACD  1. U holda  ACD  2 chunlki  1=  2. Bu burchaklar ACD uchburchakka tegishli. Katta burchak qarshisida katta tomon yotishini hisobga olsak, AC Teorema isbotlandi. Bu teoremadan quyidagi natija kelib chiqadi. Natija: Bir to’g’ri chiziqda yotmagan ihtiyoriy uchta A,B va C nuqta uchun AC Bu tengsizliklarning har biri uchburchak tengsizligi deyiladi. 1-masala. 2-rasmda berilgan ma’lumotlardan foydalanib,  1  3 ekanligini isbotlang Yechish:  2  3,  2-∆BDCning tashqi burchagi. Tashqi burchak xossasiga ko’ra,  2=  3+  4 va  40. ∆ACD teng yonli.  1=  2. Demak,  1  3.

Masalan:

1-misol
Reytingga oid masala yechamiz.Sinf jurnalini eslatuvchi jadval tuzamiz.Jadvaldan ko’rib turganingizdek, C7 katakchadan K7 katakchagacha yoki C7:K7 blokda birinchi, C8:K8 blokda ikkinchi …o’quvchilarning olgan reyting ballari joylashadi.O’quvchilarning fanlardan olishi mumkin bo’lgan maksimal va olgan umumiy ballari jamlanmasi L ustuga yig’iladi, ya’ni mos ravishda, L6=C6+D6+E6+F6+G6+H6+I6+J6+K6 ga teng bo’ladi.

Bu yig’indilarni turli usullarda hosil qilishimiz mumkin.Demak, L6 katakchaning nusxasi L7,L8,L9,L10 katakchalarga nisbiy murojat bilan joylashadi, shu kabi, M6=L6*100/$L$6 katakchaning nusxasi M7,M8,M9,M10 katakchalarga mos ravishda L7*100/$L$6, L8*100/$L$6,L9*100/$L$6, L10*100/$L$6 KABI JOYLASHADI. Bu yerda, $L$6- absolyut adres bo’lib,umumiy ball joylashgan katakchadir.

2-misol
y=2x+19 funksiyasi qiymatlarini x ning -5dan 21gacha bolgan toq qiymatlarida hisoblang.

a)Yurgichni B1 katakchaga joylashtiramiz;b)Tahrir (правка)meynyusining To’ldirish(Заполнить) bo’limidan Progressiya(Прогрессия) bolimini tanlaymiz;

d)Progressiya tanlov oynasida to’ldirish qadamini 2, chegaraviy qiymatni 21 kabi yozamiz.e) OK tugmasini tanlaymiz

8
T
P
1
L
2
R
V
G
A
A
3
E
e
N
N
D
R
S
4
I
5
O
o
I
P
M
m
7
T
B
M
E
e
B
6
I
E
E
O
R
T
S
U
K
t
D
T
R
A
O
r
A
R
I
S
T
R
Ch
L
I
i
I
I
G`
A
R
Ya
A
R
T
N
ya
K
I
A
R
I
S
S
A

Darsni yakunlash: o’quvchilar bilan o’tilgan mavzu yuzasidan BOSHQOTIRMA o’tkazish. O’quvchilarni baholash : o’quvchilar 1 balldan 5 ballgacha (har bir to’g’ri javob uchun yig’ib borilgan “1” ballik kartochkalar asosida) baholanadilar. Faol ishtirok etgan guruh taqdirlanadi. Uyga vazifa : 45-darsni o’qib,mashqlarni bajarish Xayrlashish

E’TIBORINGIZ UCHUN RAXMAT!!!