Саба?ты? та?ырыбы: Тікб?рышты ?шб?рышты? с?йір б?рышыны? синусы, косинусы, тангенсі ж?не котангенсі.
Саба?ты? ма?саты:
Білімділік: Тікб?рышты ?шб?рышты? с?йір б?рышыны? синусын, косинусын, тангенсін, котангенсін аны?тау, м?ндерін табуды ж?не берілген м?ндері бойынша тік б?рышты ?шб?рышты салуды ?йрету.
Дамытушылы?: Тікб?рышты ?шб?рышты? б?рыштарын, ?абыр?аларын есептеуге арнал?ан аны?тамалар, формулаларды есептер шы?аруда ?олдана білу да?дысын ?алыптастыру.
Т?рбиелік: О?ушыларды? ойлау ?абілетін жетілдіру, ?з бетінше е?бек етуге т?рбиелеу
Саба? т?рі: Жа?а білімді ме?герту
К?рнекілігі: Сызбалар, карточкалар, слайд, интерактивті та?та, сыз?ыш
Саба?ты? барысы:
1. ?йымдастыру кезе?і
2. Жа?а саба?ты баяндау
§8. Тікб?рышты ?шб?рышты? с?йір б?рышыны? синусы, косинусы, тангенсі ж?не котангенсі.
Бізге тікб?рышты ?шб?рыш, оны? катеттері мен гипотенузасы, с?йір б?рыштары ??ымдары белгілі. Б?гінгі саба?та тікб?рышты ?шб?рышты? ?абыр?алары мен б?рыштарыны? арасында?ы байланысты ?арастырамыз.
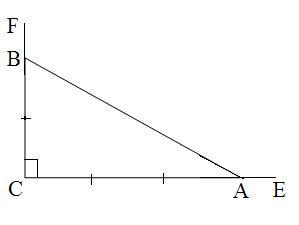
АВС тікб?рышты ?шб?рыш берілген
( 27-сурет). Оны? катеттері а, b ал гипотенузасы с деп, бір с?йір б?рышын мысалы А=α деп белгілейік. С=90º болсын.
27-сурет
Аны?тама: Тікб?рышты ?шб?рышты? с?йір б?рышына іргелес жат?ан катетті? гипотенуза?а ?атынасы сол б?рышты? косинусы деп аталады. Оны ?ыс?аша cosα= (1) т?рінде жазады. (1) ?атынас α б?рышыны? шамасына ?ана т?уелді, ?абыр?аларды? ?зынды?тарына т?уелді емес.
20-теорема. Б?рышты? косинусы мен тек оны? градусты? ?лшеміне ?ана т?уелді.
Д?лелдеу: АВС тікб?рышты ?шб?рышы берілсін. Б?л ?шб?рыш ?шін (1) те?дік орындалсын.
АВ с?улесіне AD=к.с кесіндісін (28-сурет). Ал АС с?улесіне АЕ=к.в (к-о? сан) ?лшеп саламыз. М?нда?ы, ΔADE –тікб?рышты ?шб?рыш ж?не cosα= екенін д?лелдейміз. Шынында болады. Керісінше ?й?арып, DE кесіндісін АЕ т?зуіне перпендикуляр емес делік. Сонда D н?ктесінен АЕ т?зуіне DF перпендикулярын т?сіруге болады. Н?тижесінде, ADF тікб?рышты ?шб?рышы ?шін cosα=
?атынасын жазамыз. Ал (1) те?дікті? негізінде аламыз, біра? немесе болып ?алады. Онда AE=AF ж?не cosα= шы?ады. Теорема д?лелденді.
Аны?тама. Тікб?рышты ?шб?рышты? с?йір б?рышына ?арсы жат?ан катетті? гипотенуза?а ?атынасы сол б?рышты? синусы деп аталады да,
(2)
т?рінде жазылады.
Аны?тама. Тікб?рышты ?шб?рышты? с?йір б?рышына ?арсы жат?ан катетті? іргелес жат?ан катетке ?атынасы сол б?рышты? тангенсі деп аталады. Оны
(3)
т?рінде жазады.
Аны?тама. Тікб?рышты ?шб?рышты? с?йір б?рышына іргелес жат?ан катетті? ?арсы жат?ан катетке ?атынасы сол б?рышты? катангенсі деп аталады. Оны
(4)
т?рінде жазамыз.
sinα, cosα, tgα ж?не ctgα-ларды тригонометриялы? ?рнектер деп атайды.
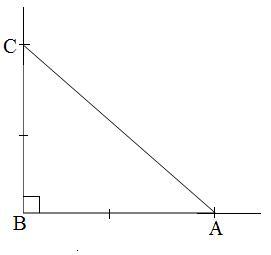
Мысалы. С?йір б?рышыны? косинусы 3:56 ?атынасына те? болатын ?шб?рышты салайы?.
Шешуі: Ізделінді тікб?рышты ?шб?рыш АВС болсын, м?нда?ы АВ=c-гипотенуза; <С=900; <A=α, BC=a, CA=b-катеттер.
cosα= те?дігі орындалу керек. Бірлік кесінді е та?дап аламыз. с?улелерін ж?ргіземіз. 29 –сурет.
СЕ с?улесіне СА=3е кесіндісін ?лшеп саламыз. Центрі А н?ктесі етіп, АВ=5a кесіндісіне те? радиус етіп ше?бер ж?ргіземіз. Ол CF с?улесін В н?ктесінде ?иып ?теді. Н?тижесінде АВС тікб?рышты ?шб?рышы салынады. Ол тікб?рышты ?шб?рышта
cosα= болады. Демек, салын?ан ?шб?рыш есепті? шартын ?ана?аттандырады.
3. Есептер шы?ару.
№118. С?йір б?рышты? синусы 1) ; 3) 0,6-?а те? тікб?рышты ?шб?рыш салы?дар.
Шешуі:
Берілгені: СЕ с?улесіне СВ=1 бірлік кесіндіні ?лшеп СВ=a=1 саламыз. Центрі В, радиусы 2-ге те? ше?бер саламыз, ол CF т?зуін А н?ктесінде ?иып ?теді. АВС ?шб?рышы есеп шартын ?ана?аттандырады.
3)
sinα=0.6
№120. С?йір б?рышты? тангенсі 1) ; 3) 1-ге те? тікб?рышты ?шб?рыш салы?дар.
1),
Шешуі: т?зулерін ж?ргізіп, СЕ с?улесіні? бойына СА=3, ал CF с?улесіні? бойына СВ=2 кесінділерін ?лшеп саламыз. АВС - ізделінді ?шб?рыш.
3) tgα=1, да а=b екені белгілі болып отыр.
4. ?орытындылау (слайд)
cosα=
Слайд бойынша ережелерді ?айталау.
5. ?йге: §8. №118(2), №119(2), №120 (2), 121 (2)
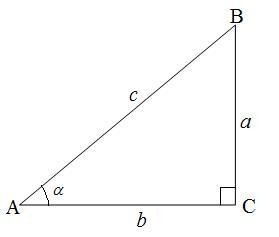
 А=α деп белгілейік.
А=α деп белгілейік. 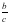 (1) түрінде жазады. (1) қатынас α бұрышының шамасына ғана тәуелді, қабырғалардың ұзындықтарына тәуелді емес.
(1) түрінде жазады. (1) қатынас α бұрышының шамасына ғана тәуелді, қабырғалардың ұзындықтарына тәуелді емес. 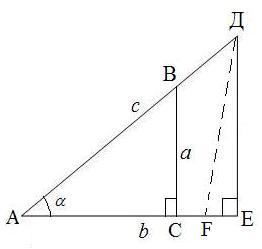
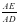 екенін дәлелдейміз. Шынында
екенін дәлелдейміз. Шынында 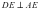 болады. Керісінше ұйғарып, DE кесіндісін АЕ түзуіне перпендикуляр емес делік. Сонда D нүктесінен АЕ түзуіне DF перпендикулярын түсіруге болады. Нәтижесінде, ADF тікбұрышты үшбұрышы үшін cosα=
болады. Керісінше ұйғарып, DE кесіндісін АЕ түзуіне перпендикуляр емес делік. Сонда D нүктесінен АЕ түзуіне DF перпендикулярын түсіруге болады. Нәтижесінде, ADF тікбұрышты үшбұрышы үшін cosα=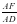
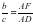 аламыз, бірақ
аламыз, бірақ 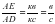 немесе
немесе 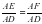 болып қалады. Онда AE=AF және cosα=
болып қалады. Онда AE=AF және cosα=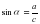 (2)
(2)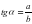 (3)
(3)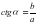 (4)
(4)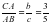 теңдігі орындалу керек. Бірлік кесінді е таңдап аламыз.
теңдігі орындалу керек. Бірлік кесінді е таңдап аламыз. 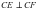 сәулелерін жүргіземіз. 29 –сурет.
сәулелерін жүргіземіз. 29 –сурет. 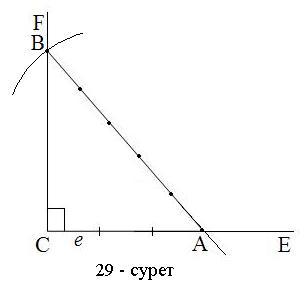
 болады. Демек, салынған үшбұрыш есептің шартын қанағаттандырады.
болады. Демек, салынған үшбұрыш есептің шартын қанағаттандырады.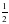 ; 3) 0,6-ға тең тікбұрышты үшбұрыш салыңдар.
; 3) 0,6-ға тең тікбұрышты үшбұрыш салыңдар.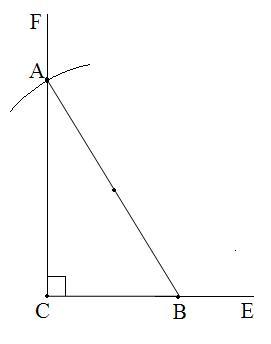
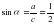 СЕ сәулесіне СВ=1 бірлік кесіндіні өлшеп СВ=a=1 саламыз. Центрі В, радиусы 2-ге тең шеңбер саламыз, ол CF түзуін А нүктесінде қиып өтеді. АВС үшбұрышы есеп шартын қанағаттандырады.
СЕ сәулесіне СВ=1 бірлік кесіндіні өлшеп СВ=a=1 саламыз. Центрі В, радиусы 2-ге тең шеңбер саламыз, ол CF түзуін А нүктесінде қиып өтеді. АВС үшбұрышы есеп шартын қанағаттандырады.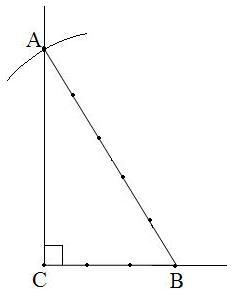
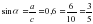
 ; 3) 1-ге тең тікбұрышты үшбұрыш салыңдар.
; 3) 1-ге тең тікбұрышты үшбұрыш салыңдар.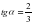 ,
, 
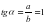 да а=b екені белгілі болып отыр.
да а=b екені белгілі болып отыр.















