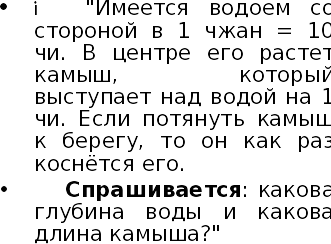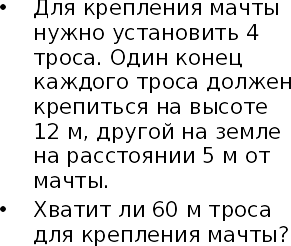Цель урока: расширить круг геометрических задач, решаемых с помощью теоремы Пифагора;
познакомить учащихся с историей теоремы, этапами жизни и деятельности Пифагора Самосского;
сформулировать и доказать теорему Пифагора
осуществить межпредметные связи геометрии с алгеброй, литературой;
развитие воображения, логического мышления, познавательной активности;
Формирование умения самостоятельной работы
Геометрия обладает двумя
великими сокровищами.
Первое – это теорема Пифагора,
Его можно сравнить с мерой золота.
Иоганн Кеплер.
План:
Практическая работа
Историческая справка
Жизнь и деятельность Пифагора
Работа над теоремой
Применение теоремы Пифагора
Исследовательская работа
Закрепление
Домашнее задание
Итоги урока
Просмотр содержимого документа
«Тік б?рышты ?шб?рышты? ?асиеті »
Боштаева Нуриппа Абдыкаимовна Город Алматы, Ауэзовский район,
школа-гимназия №13
Тема: Теорема Пифагора
Цель урока: расширить круг геометрических задач, решаемых с помощью теоремы Пифагора;
познакомить учащихся с историей теоремы, этапами жизни и деятельности Пифагора Самосского;
сформулировать и доказать теорему Пифагора
осуществить межпредметные связи геометрии с алгеброй, литературой;
развитие воображения, логического мышления, познавательной активности;
Формирование умения самостоятельной работы
Геометрия обладает двумя
великими сокровищами.
Первое – это теорема Пифагора,
Его можно сравнить с мерой золота...
Иоганн Кеплер.
План:
Практическая работа
Историческая справка
Жизнь и деятельность Пифагора
Работа над теоремой
Применение теоремы Пифагора
Исследовательская работа
Закрепление
Домашнее задание
Итоги урока
1)
2)
3)
4) Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: Δ ABC , С = 90 °
Доказать:
Доказательство:
Дано:
ABC
Найти:
BC
Дано:
ABC
Найти:
BC
Дано:
ABCD - ромб
Найти:
BC
5)
Решение: Пусть высота тополя Н футов, тогда3 2 + 4 2 = h 2 ,
h 2 = 25, h = 5; h = 5 футов – длина отломленной части ствола;
Н = 3 + 5 = 8(футов) – высота тополя. Ответ: 8(футов)
Решение: Пусть глубина водоема x чи. Тогда длина камыша ( x + 1) чи. По теореме Пифагора квадрат этой длины равен сумме квадратов глубины водоема и расстояния от центра до берега: ( x +1) 2 - x 2 =5, x 2 +2 x +1- x 2 =25, x =12 12 чи – глубина воды;
(x + 1)=13 чи – длина камыша Ответ: 13 чи
6)
7)
8)
9)